Journal of Applied Mathematics and Physics
Vol.05 No.08(2017), Article ID:78744,24 pages
10.4236/jamp.2017.58129
Numerical Approximation to Nonlinear One Dimensional Coupled Reaction Diffusion System
Shahid Hasnain, Daoud Suleiman Mashat, Muhammad Saqib, Shafeek A. Ghaleb, Noorah Y. Mshary
Department of Mathematics, Numerical Analysis, King Abdulaziz University, Jeddah, Saudi Arabia
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 8, 2017; Accepted: August 22, 2017; Published: August 28, 2017
ABSTRACT
This research paper represents a numerical approximation to non-linear coupled one dimension reaction diffusion system, which includes the existence and uniqueness of the time dependent solution with upper and lower bounds of the solution. Also numerical approximation is obtained by finite difference schemes to reach at reasonable level of accuracy, which is magnified by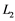 ,
, 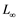 and relative error norms. The accuracy of the approximations is shown by randomly selected grid points along time level and comparison with analytical results. The test example demonstrates the accuracy, efficiency and versatility of the proposed schemes. Moreover, the schemes can be easily applied to a wide class of higher dimension non-linear reaction diffusion equations with a little modifications.
and relative error norms. The accuracy of the approximations is shown by randomly selected grid points along time level and comparison with analytical results. The test example demonstrates the accuracy, efficiency and versatility of the proposed schemes. Moreover, the schemes can be easily applied to a wide class of higher dimension non-linear reaction diffusion equations with a little modifications.
Keywords:
Forward in Time and Centre in Space (FTCS), Taylor’s Series, Crank Nicolson, Fourth Order Implicit Scheme and Richardson Extrapolation

1. Introduction
Fisher and Kolmogorov Petrovsky Piscounov founded quasilinear partial dif- ferential equation which represents reaction diffusion phenomena [1] [2] , which play important rule in population dynamics as propagation of beneficial genes; mathematical description to this phenomena is as follows [1] [2] [3] ,
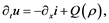 (1)
(1)
here, x declares spatial coordinate position with time t, also 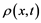 is the term used to identify the population density, i is the flux associated to population, and
is the term used to identify the population density, i is the flux associated to population, and 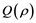 is a limited to originator term that illuminate the net rate of production or growth in the populated area or density associated to population [3] . The be- haviour of the diffusion is accounted in the flux i, inclines by Fick’s law,
is a limited to originator term that illuminate the net rate of production or growth in the populated area or density associated to population [3] . The be- haviour of the diffusion is accounted in the flux i, inclines by Fick’s law,
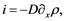 (2)
(2)
where the assumption on the diffusion coefficient D, is to be constant [3] . It is frequently to imitate the law, which is known as the Pearl-Verhulst logistic law,
 (3)
(3)
related to stranded scale to growth in the population [3] . This law explains the that initially population would grow with homogeneous fashion with time of 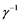 until that growth reach at some stranded level with some saturation in population [3] . Fisher and KPP were very much keen about the speed that exists in advantageous genes to propagate and they found a travelling wave solution to Equations (1), (2), (3) [3] , such solution related to velocity
until that growth reach at some stranded level with some saturation in population [3] . Fisher and KPP were very much keen about the speed that exists in advantageous genes to propagate and they found a travelling wave solution to Equations (1), (2), (3) [3] , such solution related to velocity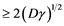 . Con- sequential, Kametaka (1976) and Uchiyama (1977)] remarks about velocity of
. Con- sequential, Kametaka (1976) and Uchiyama (1977)] remarks about velocity of 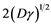 developed initial conditions (ICs), categorised as [3] ,
developed initial conditions (ICs), categorised as [3] ,
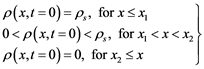 (4)
(4)
2. Governing Equation
In the year of 1948 El’ dovich, raised the major features of the diffusion reaction semi-linear equation which make useful contribution to wave of advantageous genes which are now totally classify as in the dynamics of the gas and flame with chemical kinetics [3] . Mostly, in process of combustion, the concept of heat which is channelized by the conduction processed by heat related to molecules which moves from the hot part of flame to coolant side [3] , by a particular locality, the rate of the chemical reaction such as exothermic chemical reaction (due to presence of heat), totally aware of temperature of the related gas mixture [3] . The coefficients associated with molecular diffusion and thermal are at same level of scaled, the temperature and concentration are situated almost isobaric [3] . The quantity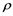 , then can represent either the temperature or concentration, without confusion, and is often referred to as the “combustion completeness by such coefficient” by Vulis, 1961 [3] . Equations (1)-(4) are then hired to modelled this attractive phenomena as a result of travelling wave nature of the flame exists in combustion process or zone, i.e. the transition layer between the region of burnt gas and the gas where combustion has not yet begun [3] . Above literature review, leads to the following reaction-diffusion system in two components along single direction, is as follows,
, then can represent either the temperature or concentration, without confusion, and is often referred to as the “combustion completeness by such coefficient” by Vulis, 1961 [3] . Equations (1)-(4) are then hired to modelled this attractive phenomena as a result of travelling wave nature of the flame exists in combustion process or zone, i.e. the transition layer between the region of burnt gas and the gas where combustion has not yet begun [3] . Above literature review, leads to the following reaction-diffusion system in two components along single direction, is as follows,
 (5)
(5)
where in above Equation (5), 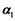 and
and 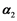 are the linear growth rate whereas
are the linear growth rate whereas 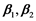 are coefficients of the diffusion [3] [4] [5] , with
are coefficients of the diffusion [3] [4] [5] , with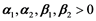 , as well as
, as well as 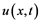 and
and 
3. Exact Solution
Exact solution to system in Equation (5) found by E. S. Fahmy [5] , he used factorization method, given below:


4. Smoothness and Uniqueness of the Reaction Diffusion System
It is very important to enforce some assumptions on some physical parameters or related reaction functions, to analysed the smoothness and uniqueness of a positive oriented natural solution by considering lower and upper bound of the solution of the system which mentioned in Equation (5) [6] . We assume that 




imposed the following boundary conditions on Equation (8), which is,

imposed the following initial conditions on Equation (8), which is,

combined above three equations, to get the model system.
Assumption or Hypothesis (H)
Let us suppose that 








where above Equations (11), (12) represents 


4.1. Definition
A smooth pair of two vector functions



In the above definitions the smoothness of

4.2. Theorem
Let f holds hypothesis (H). If there exist upper and lower solutions







The quality of being of practical use about above theorem, need to construct of lower and upper solutions, with existence problem to be ensured [6] , but the asymptotic behaviour of the time-dependent solution and related stability can also be established from the behaviour of the lower and upper solutions [6] , ac- cording to the definition, so stability of a steady-state solution make according to selection of Lyapunov function [6] , be that as it may for the global existence problem or the stability problem with homogeneous boundary conditions [6] .
5. Numerical Methods
Let us apply numerical methods technique, to solve such system which men- tioned in Equation (5) in finite domain



5.1. Forward in Time and Centre in Space (FTCS) Scheme
We consider forward in time and center in space (FTCS) explicit scheme by substituting the forward difference approximation for the time derivative and the central difference approximation for the space derivative in system in Equation (5),


where



Finite difference schemes, must pass certain tests of accuracy, consistency, stability and convergence [9] [10] [11] , we discuss these concepts in the follow- ing way.
5.1.1. Accuracy of FTCS
Accuracy of the FTCS scheme for system in Equation (16), we apply Taylor’s series on each term, which is as follows:

simplifies above equations, we get the following,

dividing above system, by k and simplifies some terms:

This leads to principle part of the truncation error (PPTE), which is as follows:

which shows that this scheme has 2nd order accuracy in space and first order accuracy in time such as 
5.1.2. Consistency of FTCS
According to the definition of the consistency, if the difference between finite difference equation (FDE) and related partial differential equation (PDE), i.e truncation error vanishes as the sizes of the grid spacing go to zero inde- pendently, i.e

Equation (20) is consistent, because the truncation error divided by k tends to zero as h and k tends to zero [11] [12] [13] [14] .
5.1.3. Convergence of FTCS
A finite difference method is convergent if the solution of the finite difference equation approaches to exact solution of the partial differential equation as the sizes of the grid spacing h and k tends to zero [13] [14] [15] .

where 

where 


this completes the proof of the convergence.
5.1.4. Stability of FTCS
Another important feature of a finite difference method of solving partial dif- ferential equation is the stability of the associated finite difference equation which must be investigated. Let us look again Equation (16),

linear form of above Equation (26), is as follows:

where
where

where
where matrix 

above Inequality (29) leads to the following two special cases,
1) Special Case 1
・ The right hand side of the Inequity (29) gives,

which is condition of stability to FTCS scheme in coupled non-linear PDE system.
2) Special Case 2
・ The left hand side of the Inequity (29) gives,

which is condition of stability to FTCS scheme in coupled non-linear PDE system.
Special case (1) and special case (2) lead to the following very interesting results,

The Von-Neumann stability analysis is the most common used method of de- termining stability criterion as it is generally the easiest to apply. It can only be used to establish a necessary and sufficient condition for stability of linear initial value problems with constant coefficients [14] [15] [16] [17] [18] [19] . Thus according to Von-Neumann stability analysis, FTCS scheme is conditionally stable as obtained in Equation (32).
5.2. Crank Nicolson Implicit Scheme
Let us apply Crank Nicolson implicit finite difference scheme to Equation (5).

after some simplification, we get the following,


combine Equations (34) (35), we get the following,

where 

5.2.1. Accuracy of CN
Accuracy of the CN scheme to Equation (36), we apply Taylor’s series on each term. After some simplification, resultant is as follows,


we divide above equation by time step k with using in system (5), to get the accuracy, in the following form,



Now principle part of the truncation error (PPTE) is as follows:

which shows that this scheme is 2nd order accurate in both time and space, such as 
5.2.2. Consistency of CN
From accuracy, we find principle part of the truncation error along with Equ- ation (42). Which shows that Crank Nicolson scheme is consistent because 


5.2.3. Stability of CN
Stability of the associated finite difference Equation (36), which is in linear form,

where 

where 

According to Von-Neumann stability analysis, we have

where
where matrix 


Above Equation (46), satisfies the Von-Neumann stability criterion, which shows that CN scheme for Equation (5) is unconditionally stable [21] [22] [23] [24] [25] .
5.3. Fourth Order Accurate Implicit Scheme
Let us apply another implicit scheme with improved accuracy in space to Equation (5).


where



combine Equations (49) (50), to get the following,

where



5.3.1. Accuracy of Douglas Scheme
Accuracy of the Douglas scheme to Equation (36), we apply Taylor’s series on each term. After some simplification, resultant is as follows,




Dividing above Equations (54) and (55) by k and take into account Equation (5), so resultants are as follows:

let us look above equation in new way,

Now principle part of the truncation error (PPTE) is as follows:

which shows that this scheme is 4th order accurate in space, such as 
5.3.2. Consistency of Douglas Scheme
From accuracy, we find principle part of the truncation error along with Equ- ation (58). Which shows that Douglas scheme is consistent because 


5.3.3. Stability of Douglas Scheme
Stability of the associated finite difference Equation (51), which is in linear form, is


Consider Equations (44) (60), in the following few important steps.

Apply Von-Neumann stability analysis to Equation (60), we get the following


Above Equation (63), satisfies the Von-Neumann stability criterion, which shows that fourth order implicit scheme is unconditionally stable [33] [34] [35] [36] [37] .
5.4. Richardson Extrapolation Technique
Richardson extrapolation method lead to considerable improvement of numerical results which solving the partial differential equation system by finite difference method. Richardson’s extrapolation formulae are [38] [39] ,

above formula leads to get fourth order accuracy [39] [40] ,

6. Error Norms
The aim of the accuracy is assessed by some redefined norms, associated with the consistency of the finite difference schemes, such scaled measurement to error defined in term of norms specially 






where 



7. Results
Numerical computations have been performed using the uniform grid [14] [21] [25] [29] . For the test problem (5), we analysed results with various finite difference schemes. In Tables 1-3, we fixed domain as 



Table 1. Estimates of results using Crank Nicolson Implicit Scheme. Fixed some para- meters such as



Table 2. Estimates of results using Fourth Order Implicit Scheme. Fixed some parameters such as



Table 3. Estimates of results using Sixth Order Extrapolation Method. Fixed some parameters such as



Table 4. Estimates of results, with comparison of errors as mentioned in formulae. Fixed some parameters such as


Table 5. Estimates of results, with two different Implicit FD schemes. Relative error values give encouragement to our results. Fixed some parameters as
schemes CN and Douglas at different grids and time levels. Rate of convergence is defined in Table 6. All these six tables show results for three implicit scheme to analyse error and performance of the schemes. According to results men- tioned in tables, these scheme play very important role for convergence although non-linear system is difficult to stabilized. In Figure 1, FTCS conditionally stable finite difference scheme is used at different grid, also we did in Figure 2 with Crank Nicolson implicit scheme. Fixed some parameters in CN scheme to get common region at different time level, as we mentioned in Figure 3. In Figure 4 and Figure 5, we did comparison of results with two different schemes at various time levels. In Figure 6 and Figure 7 attractive common region at different time level is obtained. In Figures 8-10, comparison of results with Richardson, Douglas and exact in 


8. Conclusions
In this chapter, the solution to one dimensional coupled Fisher KPP system is successfully approximated by a various numerical finite difference schemes. Explicit FTCS is conditionally stable, and we give more attention to parameter R1 and R2, which can be used to stabilized the results as we can see from Figure 1. Crank Nicolson and Douglas schemes are implicit schemes with uncondi- tionally stable nature, this guarantee is given by Von-Neumann stability analysis
Table 6. Estimates the rate of convergence for two implicit FD schemes for different grids.
Figure 1. Shows results using FTCS scheme at two different grids, keeping the conditionally stable term. Area under the curves is the common region for two different grids.
Figure 2. Shows results using Crank Nicolson scheme at two different grids.
Figure 3. Shows results using Crank Nicolson scheme at two different time level. Common region is the wave front that we study in literature [35] [39] [41] .
Figure 4. Shows results using Crank Nicolson scheme at various time levels. We did comparison with exact solution for 

Figure 5. Shows results using fourth order implicit scheme at various time levels. We did comparison with exact solution for 

Figure 6. Shows fourth order implicit scheme at three different time level. Common region is the wave front that we study in literature [17] [23] [29] [41] .
Figure 7. Shows results using fourth order implicit scheme at various time levels, with common region.
Figure 8. Shows results using Richardson Extrapolation and fourth order implicit scheme, with comparison to exact solution for u component.
Figure 9. Shows results using Richardson Extrapolation and fourth order implicit scheme, with comparison to exact solution for 
Figure 10. Shows results using Richardson Extrapolation at different time levels, along fourth order implicit scheme.
Figure 11. Shows a comparison of two schemes in u(x,t)/v(x,t) form, with exact solution.
as we explained in methodology section [27] [28] [29] [31] [35] [36] . Jacobean found with the help of Newton’s iterative method [36] [38] , whereas tridiagonal nature of the linear obtained system is solved by Crout’s or Partially Pivoting method. These method are highly computable in term of non-linear system as we defined in this chapter [40] [41] [42] . Numerical results show great deal of match- ability to exact solution. Accuracy in results are glanced from figures and tables.
Acknowledgements
Shahid Hasnain, Prof. Daoud Mashat and Muhammad Saqib is thankful to Dr Muhammad Faheem Afzaal, Department of Chemical Engineering, Imperial College London and Vineet K. Srivastava, Scientist, ISTRAC/ISRO, Bangalore, India for thoughtful remarks. This research was supported by Department of Mathematics, division of Numerical Analysis, King Abdulaziz University, Jeddah, Saudi Arabia.
Conflict of Interest
There is no conflict of interest in this research paper.
Cite this paper
Hasnain, S., Mashat, D.S., Saqib, M., Ghaleb, S.A. and Mshary, N.Y. (2017) Numerical Approximation to Nonlinear One Dimensional Coupled Reaction Diffusion System. Journal of Applied Mathematics and Physics, 5, 1551-1574. https://doi.org/10.4236/jamp.2017.58129
References
- 1. Fisher, R.A. (1936) The Wave of Advance of Advantageous Genes. Annals of Eugenics, 7, 355-369. https://doi.org/10.1111/j.1469-1809.1937.tb02153.x
- 2. Kolmogorov, A.K., Petrovsky, N.P. and Piscounov, S.P. (1937) Etude de I equations de la diffusion avec croissance de la quantitate de matiere et son application a un probolomebiologique. Bulletin Univercity Mosku, 1, 1-25.
- 3. Newman, W.I. (1980) Some Exact Solutions to a Non-Linear Diffusion Problem in Population Genetics and Combustion. Journal of Theoretical Biology, 85, 325-334.
- 4. Ronson, D.G. and Weinberger, H.F. (1975) Lecture Notes in Mathematics 446, Partial Differential Equations and Related Topics. Springer-Verlag, Berlin, 5-49.
- 5. Fahmy, E.S. (2009) Exact Solutions for Some Reaction Diffusion Systems with Nonlinear Reaction Polynomial Terms. Applied Mathematical Sciences, 3, 533-540.
- 6. Pao, C.V. (1981) Asymptotic Stability of Reaction-Diffusion Systems in Chemical Reactor and Combustion Theory. Journal of Mathematical Analysis and Applications, 82, 503-526.
- 7. Franak Kameneetiskii, D.A. (1969) Diffusion and Heat Transfer in Chemical Kinetics. Plenum Press, New York.
- 8. Bramson, M.D. (1978) Maximal Displacement of Branching Brownian Motion. Communications on Pure and Applied Mathematics, 31, 531-581. https://doi.org/10.1002/cpa.3160310502
- 9. Canosa, J.C. (1973) On a Nonlinear Diffusion Equation Describing Population Growth. IBM Journal of Research Development, 17, 307-313. https://doi.org/10.1147/rd.174.0307
- 10. Arnold, R.A., Showalter, K. and Tyson, J.J. (1987) Propagation of Chemical Reactions in Space. Journal of Chemical Education, 64, 7740-7744. https://doi.org/10.1021/ed064p740
- 11. Tuckwell, H.C. (1988) Introduction to Theoretical Neurobiology. Cambridge University Press, Cambridge.
- 12. Mittal, R.C. and Rajni, R.R. () A Study of One Dimensional Nonlinear Diffusion Equations by Bernstein Polynomial Based Differential Quadrature Method. Journal of Mathematical Chemistry, 55, 673-695.
- 13. Burgers, J.M. (1948) A Mathematical Model Illustrating the Theory of Turbulence. Advances in Applied Mechanics, 1, 171-199.
- 14. Bateman, H.B. (1915) Some Recent Researches on the Motion of Fluids. Monthly Weather Review, 43, 163-170. https://doi.org/10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2
- 15. Cole, J.D. (1950) On a Quaslinear Parabolic Equations Occurring in Aerodynamics. Applied Mathematics, 9, 201-230.
- 16. Hopf, E.H. (1951) The Partial Differential Equation . Communications on Pure and Applied Mathematics, 3, 225-236.
- 17. Wang, X.Y. (1988) Exact and Explicit Solitary Wave Solutions for the Generalized Fishers Equation. Physics Letters A, 131, 227-279.
- 18. Wazwaz, A.M. and Gorguis, A.G. (2004) An Analytic Study of Fisher’s Equation by Using Adomian Decomposition Method. Applied Mathematics and Computation, 154, 609-620.
- 19. Dag, I.D., Sahin, A.S. and Korkmaz, A.K. (2010) Numerical Investigation of the Solution of Fisher’s Equation via the B-Spline Galerkin Method. Numerical Methods for Partial Differential Equations, 26, 1483-1503.
- 20. Rahman, K.R., Helil, N.H. and Yimin, A.R. (2010) Some New Semi-Implicit Finite Difference Schemes for Numerical Solution of Burgers Equation. International Conference on Computer Application and System Modeling, 14, 451-455.
- 21. Gazdag, J.G. and Canosa, J.C. (1974) Numerical Solutions of Fisher’s Equation. Journal of Applied Probability, 11, 445-457. https://doi.org/10.1017/S0021900200096236
- 22. Abdullaev, U.G. (1994) Stability of Symmetric Travelling Waves in the Cauchy Problem for the KPP Equation. Differential Equations, 30, 377-386.
- 23. Logan, D.J. (1994) An Introduction to Nonlinear Partial Differential Equations. Wiley, New York.
- 24. Evans, D.J. and Sahimi, M.S. (1989) The Alternating Group Explicit (AGE) Iterative Method to Solve Parabolic and Hyperbolic Partial Differential Equations. Annals of Numerical Fluid Mechanics and Heat Transfer, 2, 283-389.
- 25. Tang, S.T. and Weber, R.O. (1991) Numerical Study of Fisher’s Equations by a Petrov-Galerkin Finite Element Method. Journal of the Australian Mathematical Society Series B, 33, 27-38. https://doi.org/10.1017/S0334270000008602
- 26. Khaled, K.A. (2001) Numerical Study of Fisher’s Diffusion Reaction Equation by the Sinc Collocation Method. Journal of Computational and Applied Mathematics, 137, 245-255.
- 27. Ames, W.F. (1965) Nonlinear Partial Differential Equations in Engineering. Academic Press, New York.
- 28. Ames, W.F. (1969) Finite Difference Methods for Partial Differential Equations. Academic Press, New York.
- 29. Noye, J.N. (1981) Nonlinear Partial Differential Equations in Engineering. North-Holland Publishing Comp. Conference in Queen’s College, University of Melbourne.
- 30. Mittal, R.C. and Kumar, S.K. (2009) Numerical Study of Fisher’s Equation by Wavelet Galerkin Method. International Journal of Computer Mathematics, 83, 287-298. https://doi.org/10.1080/00207160600717758
- 31. Mehdi, M.B. and Khojasteh, D.S. (2013) A Highly Accurate Method to Solve Fisher’s Equation. Pramana, 78, 335-346.
- 32. Ablowitz, M.J. and Zeppetella, A.Z. (1979) Explicit Solutions of Fisher’s Equation for a Special Wave Speed. Bulletin of Mathematical Biology, 41, 835-840. https://doi.org/10.1007/BF02462380
- 33. Wasow, W.W. (1955) Discrete Approximation to Elliptic Differential Equations. Mathematical Physics, 6, 81-97.
- 34. Schiesser, W.E. and Griffiths, G.W. (2009) A Compendium of Partial Differential Equation Models. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511576270
- 35. Whitham, G.B. (1974) Linear and Nonlinear Waves. John Wiley Sons, Hoboken.
- 36. Babuska, I.B. (1968) Numerical Stability in Mathematical Analysis. IFIP Consress, North-Holland, Amsterdam, 11-23.
- 37. Deghan, M.D., Asgar, H.A. and Mohammad, S.M. (2007) The Solution of Coupled Burgers Equations Using Adomian-Pade Technique. Applied Mathematics Computation, 189, 1034-1048.
- 38. Lax, P.D. and Wendroff, B.W. (1960) Systems of Conservation Laws. Communications on Pure and Applied Mathematics, 13, 217-237. https://doi.org/10.1002/cpa.3160130205
- 39. Kanti, P.K. and Lajja, V.L. (2011) A Note on Crank-Nicolson Scheme for Burgers Equation. Applied Mathematics, 2, 888-899.
- 40. Roache, P.J. (1972) Computational Fluid Dynamics. Hermosa, Albuquerque.
- 41. Mazumder, S.M. (2015) Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods. Academic Press, New York.
- 42. Srivastava, V.K. and Tamsir, M.T. (2012) Crank Nicolson Semi Implicit Approach for Numerical Solution of Two Dimensional Coupled Non-Linear Burger’s Equations. International Journal of Applied Mechanics and Engineering, 17, 571-581.


















