Journal of Applied Mathematics and Physics
Vol.04 No.10(2016), Article ID:71366,7 pages
10.4236/jamp.2016.410192
Measurement of Mathematical Constant p and Physical Quantity Pi
Milan Perkovac
University of Applied Sciences, Zagreb, Croatia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 13, 2016; Accepted: October 17, 2016; Published: October 20, 2016
ABSTRACT
Instead of calculating the number p in this article special attention is paid to the method of measuring it. It has been found that there is a direct and indirect measurement of that number. To perform such a measurement, a selection was made of some mathematical and physical quantities which within themselves contain a number p. One such quantity is a straight angle Pi, which may be expressed as Pi = p rad. By measuring the angle, using the direct method, we determine the number p as p = arccos(−1). To implement an indirect measurement of the number p, a system consisting of a container with liquid and equating it with the measuring pot has been conceived. The accuracy of measurement by this method depends on the precision performance of these elements of the system.
Keywords:
Pi, Greek Letter p, Angle Measurement, Measuring Pot, Radian

1. Introduction
The number p is a mathematical and physical constant which originated as the ratio of a circle’s circumference to its diameter. Throughout scientific history it became significant as it appeared across all fields of mathematics and physics having little to do with the geometry of circles. Some of those fields are mathematical number theory, statistics, cosmology, thermodynamics, mechanics, quantum mechanics and electromagnetism. Great efforts have been invested in finding as many decimal digits of that number as it is possible. On the contrary, in this article we focus on the measurement associated with the mathematical constant p and the physical quantity Pi. So, essentially we have to distinguish two different things, the number p and the physical quantity Pi. Many have focused exclusively on the calculation of the number p and not to measure it. To be able to measure it, we need to find a link between the number p and the physical quantity Pi.
2. Definition of the Radian
The radian is the standard unit of angular measure. By definition, the radian (symbol rad) is the plane angle unit in the International System of Units (abbreviated SI). It represents the central angle on a circumference and covers an arc  whose length
whose length  is equal to the radius r of the circuit (Figure 1):
is equal to the radius r of the circuit (Figure 1):
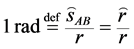 . (1)
. (1)
It is one of two supplementary units in SI; namely, radian-for plane angles, and steradian (symbol sr)-for solid angles, based on abstract geometrical concept rather than physical standards.
Any angle  formed by two radii, measured in radians, is equal to the arc length between two spokes
formed by two radii, measured in radians, is equal to the arc length between two spokes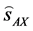 , divided by radius r (Figure 1). So, the full angle
, divided by radius r (Figure 1). So, the full angle 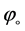 (360˚) is:
(360˚) is:
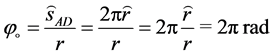 , (2)
, (2)
where  is a transcendental number, i.e., a fundamental mathematical constant with the decimal expansion 3.141592653…, tens of billions of decimal places have been calculated; just 39 places suffice to compute the circumference of the observable universe accurate to within the radius of a hydrogen atom. The number
is a transcendental number, i.e., a fundamental mathematical constant with the decimal expansion 3.141592653…, tens of billions of decimal places have been calculated; just 39 places suffice to compute the circumference of the observable universe accurate to within the radius of a hydrogen atom. The number 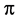 is sometimes known as Archimedes’ constant or Ludolph’s constant, after Ludolph van Ceulen (1539-1610), a German-Dutch mathematician [1] .
is sometimes known as Archimedes’ constant or Ludolph’s constant, after Ludolph van Ceulen (1539-1610), a German-Dutch mathematician [1] .
We should distinguish two different things; first, the mention number 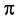 and a second, the mathematical and physical quantity denoted by Pi. While p is a number, Pi is a quantity defined as the ratio of the circumference of a circle (
and a second, the mathematical and physical quantity denoted by Pi. While p is a number, Pi is a quantity defined as the ratio of the circumference of a circle (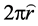 ) to its diameter (d = 2r). Actually, according to the definition of radian, and using Equation (2), the quantity Pi is the angle, because is defined as any angle:
) to its diameter (d = 2r). Actually, according to the definition of radian, and using Equation (2), the quantity Pi is the angle, because is defined as any angle:
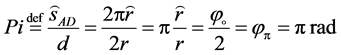 . (3)
. (3)
There are many formulas for calculating the number p, from the simple to the very
Figure 1. Description of radian (1 rad), straight angle , full angle
, full angle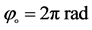 , and arc length
, and arc length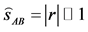 ; the symbol “
; the symbol “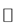 ” in the appropriate scale means “corresponds to”.
” in the appropriate scale means “corresponds to”.
complicated. While many researchers’ oriented to calculating the number p in the largest possible number of decimals, we will focus here our efforts at something else, namely, how to measure the mathematical and physical quantity Pi.
All the measurable quantities are physical quantities. The measurement is associated with unit (rad, in our case) and numerical value, like number p in Equation (3):
 . (4)
. (4)
In general, the quantities can be measured directly or indirectly. E.g. measuring the length of road, weight of body and so on, are the direct measurement. Measuring the mass of Earth, electron, and so on are indirect measurement. Measuring of the quantity Pi can be made both ways, directly and indirectly.
3. Direct Measurement of the Quantity Pi
Formula for the arc length 

read [2] :

The derivative of Equation (5) is equal to

so

When the arc length 


i.e.,

then the corresponding angle, according to the definition in Equation (1), is equal to 1 rad (Figure 1). In this way chosen is the arc that belongs to the angle of one radian. With this arc, as units of measurement (


In this way we can directly measure the length of the arc belonging to the angle


The numeric value in such measurement of the arc 

4. Indirect Measurement of the Quantity Pi
The quantities that cannot be measured are the aphysical quantities. They do not have any scale to measure. They are also called the abstract quantities and are considered not to be present in this physical world. The quantity Pi certainly does not belong in the abstract quantities. This article presents some of the methods of indirect measurement the physical quantity Pi.
To perform measurements the presented method uses liquid in a container of any shape which volume is Vc (Figure 2), relying on the document which is in the process of obtaining a patent in the UK [3] . The bottom surface of the measuring pot of any shape is

where k is a constant dependent on the shape of the bottom surface; xm is a variable, which depends on both the shapes of containers and measuring pots, and which is also the calibration parameter.
When the entire content of the liquid from the container is poured into the measuring pot, and the height of the liquid reaches the amount h, using Equation (13) (Figure 2) we get:

The shape and dimension of the measuring pot can be chosen at our will. We can choose them such that height h of liquid in the measuring pot is:

where this relation is a requirement for calibration of the system. Now Equation (14) reads as follows:
Figure 2. Perspective view of the container Vc of any shapes and the measuring pot Vm as well as of any shapes but with the bottom surface of which can be displayed as

where we get

To perform independent measurements of the number p we should get rid of it from Expression (17). This can be achieved by choosing the container which volume Vc depends on the number p, what gives us to possibility to eliminate the number p from Equation (17).
5. Calibration of the Measuring System
The easiest way to measure the number p using the system shown in Figure 2, is by using Equation (4) and Equation (15):

which means that for selected xm [according to Equation (17)] and after that fixed for a given system, the number p in this system is proportional to the height of the liquid column h in the measuring pot.
A unit of measurement is a magnitude of a quantity, defined an adopted by convention or by law, that is used as a standard for measurement of the same quantity. This means that in our system we can at will choose xm as a unit of measurement. This further means that xm corresponds to the unit; i.e.,

Using the above described system of calibration we can made different forms of containers and measuring pots, and they can realize a few systems of measurement (Table 1).
The two combinations of system to measure the number p, resulting from Table 1, are shown in Figure 3 and Figure 4.
6. Conclusion
The direct and indirect measurements of the number p have been shown. To be able to do that, the difference between the number p and physical quantity Pi has been explained. It has been shown that physical quantity Pi is actually a stretched angle, while p is a number which characterizes this angle. The idea (in patent application process) according to which the content of the liquid from the container equated with the content of measuring pot and so allowed us to use the measuring pot scale to directly read the number p has been used. Measurement accuracy of such a system depends on the precision performance of containers and measuring pots, and the conditions in which such measurement is made (type of liquid, ambient temperature and tilt of the system). The
Table 1. Various exemplary embodiments measuring pots and containers, and their pairing.
a. Ref. [4] , b. In that case the number p must be known before the measurement.
Figure 3. Perspective view of the sphere as a container Vc and rectangular cuboid as a measuring pot Vm.
simplest implementation is the use of a cylinder as container and cuboid as a measuring pot (Figure 4).
Acknowledgements
The founding of this paper is, each in its own special way, contributed by Ms. Srebrenka Ursic, Mr. Branko Balon, Mr. Damir Vuk and especially Mr. Zlatko A. Voloder.
Figure 4. Perspective view of the cylinder as a container Vc and rectangular cuboid as a measuring pot Vm.
They all have my gratitude.
Cite this paper
Perkovac, M. (2016) Measurement of Mathematical Constant p and Physical Quantity Pi. Journal of App- lied Mathematics and Physics, 4, 1899- 1905. http://dx.doi.org/10.4236/jamp.2016.410192
References
- 1. http://mathworld.wolfram.com/Pi.html
- 2. Bronstein, I.N. and Semendjajev, K.A. (1964) Matematicki prirucnik, Tehnicka knjiga, Zagreb.
- 3. Perkovac, M. and Voloder, A.Z. (2016) Method and Teaching Aid for Measuring the Value of Mathematical Constant Pi Using Liquid. Patent Application Nr. GB1612615.3.
- 4. http://mathworld.wolfram.com/Torus.html






