ABSTRACT

We study the relation between the possibility of describing quantum correlation with hidden variables and the existence of the Bloch sphere. We derive some proposition concerning a quantum expected value under an assumption about the existence of the Bloch sphere in N spin-1/2 systems. However, the hidden variables theory violates the proposition with a magnitude that grows exponentially with the number of particles. Therefore, we have to give up either the existence of the Bloch sphere or the hidden variables theory. We show that the introduction of curved information and the continuity equation of probability are in agreement with classical quantum mechanics. So we give up the hidden variable theory as local theory and we accept the Bloch sphere as global theory connected with the information space.

Keywords:

Quantum Non Locality, Formalism

1. Introduction

The quantum theory (cf. [1] - [6] ) gives approximate but frequently remarkably accurate numerical predictions. Much experimental data approximately have fit to the quantum predictions for the past some 100 years. We do not doubt the correctness of the quantum theory. The quantum theory also says new science with respect to information theory. The science is called the quantum information theory [6] . Therefore, the quantum theory gives us very useful another theory in order to create new information science and to explain the handling of raw experimental data in our physical world.

As for the foundations of the quantum theory, Leggett-type non-local variables theory [7] is experimentally investigated [8] [9] [10] . The experiments report that the quantum theory does not accept Leggett-type non-local variables interpretation. However, there are debates for the conclusions of the experiments. See Refs. [11] [12] [13] .

As for the applications of the quantum theory, the implementation of a quantum algorithm to solve Deutsch’s problem [14] on a nuclear magnetic resonance quantum computer is reported first [15] . The implementation of the Deutsch-Jozsa algorithm on an ion-trap quantum computer is also reported [16] . There are several attempts to use single-photon two-qubit states for quantum computing. Oliveira et al. implement Deutsch’s algorithm with polarization and transverse spatial modes of the electromagnetic field as qubits [17] . Single-photon Bell states are prepared and measured [18] . In addition, the decoherence-free implementation of Deutsch’s algorithm is reported using such single photon and using two logical qubits [19] . More recently, a one-way- based experimental implementation of Deutsch’s algorithm is reported [20] . In 1993, the Bernstein-Vazirani algorithm was reported [21] [22] . It can be considered as an extended Deutsch-Jozsa algorithm. In 1994, Simon’s algorithm was reported [23] . Implementation of a quantum algorithm to solve the Bernstein-Vazirani parity problem without entanglement on an ensemble quantum computer is reported [24] . Fiber-optics implementation of the Deutsch-Jozsa and Bernstein-Vazirani quantum algorithms with three qubits is discussed [25] . A quantum algorithm for approximating the influences of Boolean functions and its applications is recently reported [26]

We study the relation between a significant specific hidden variables theory and the existence of the Bloch sphere. The results of measurements are either +1 or −1. We derive some proposition concerning a quantum expected value under an assumption about the existence of the Bloch sphere in N spin-1/2 systems. However, the hidden variables theory violates the proposition with a magnitude that exponentially grows with the number of particles. Therefore, we have to give up either the existence of the Bloch sphere or the hidden variables theory. We solve the previous dilemma we introduce the information space and the continuity equation to show how quantum mechanics is consequence of the information locate in all the space so is impossible to represent by local hidden variables. In conclusion, we agree on the existence of the Bloch sphere.

2. From Probability Continuity Equation and Information Space to Shrodinger Equation

1) Continuity equation

Given the continuity equation of the probability (global conservation of the probability) we have

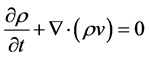(1)

when the probability density 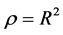we have

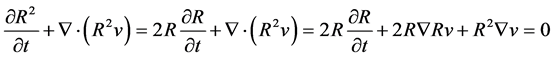(2)

For 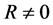we have

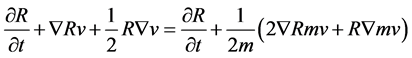(3)

Now in classical mechanics we have for the action S the relation

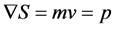(4)

So

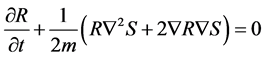(5)

where S is the action and for the wave the phase of the wave.

2) Condition probability from statistical parameters (average value, standard deviation and others)

We assume that to found a particle in a particular state is a probabilistic phenomenon for which we have join probability that the particle can be in a particular state. Now the novelty is to assume that the probability is function of other external elements as parameters. The average of the position for the particle is a parameter the movement of the particle in a particular environment for example inside of a tube or in other boundary condition (see boundary condition in Shrodinger solution) can change the probability for a particular state. Any far or near change of the environment change the probability of the state (Bell theorem and entanglement) In conclusion the join probability of a state of different variables is conditioned by a set of parameters that statically or physically can define the environment where the particle move. We denote all this parameters as the information relate to the environment where the particle is located. The set of external parameters is the information space that can have curvature as in the Berry phase phenomena that show that in the Shrodinger solution any loop can change the original phase. In differential geometry any loop in a space with curvature changes the original phase of the vectors. Now we built the information space which geodesic tensor is the Fisher entropy or Fisher information by which we can compute the covariant derivatives and the curvature.

Given the system of the conditional probabilities

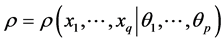(6)

We have the 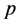dimensional information reference

(7)

Given the vector

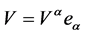(8)

The derivative is

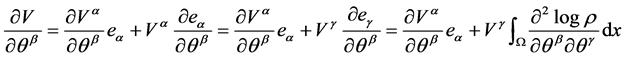(9)

where

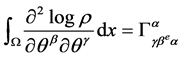(10)

is the Fisher information matrix connected with the Christoffel symbols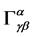. For

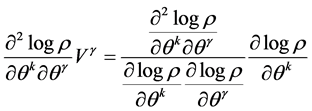(11)

Here,

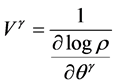(12)

For the Fisher information we have

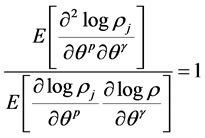(13)

where E is the average operator so we can write in the first approximation

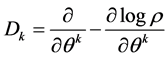(14)

and

(15)

where is the momentum. So we have

(16)

(17)

and

(18)

So

(19)

Now for and the Plank constant is equal to 1 we have

(20)

So we have

(21)

where Q is the Bohm quantum potential that is a consequence for the extreme condition of Fisher information (minimum or maximum condition for the Fisher information). We know that the quantum potential as real part and the continuous equation as the imaginary part from the Boltzmann entropic geometry we can generate the Schrödinger equation. We can also use the Schrodinger equation and came back to the Fisher information and to the pure conditional probability interpretation of the quantum mechanics.

Now, we combine the continuity equation of the probability with the covariant derivative in the curved information space we have

(22)

(23)

where the real part is consequence of the curvature in the information space and the immaginary part is due to the continuous equation for the probability.

Now for the previous real and complex part are the real and immaginary of the classical Schrodinger equation.

(24)

with

(25)

In conclusion, we can make a reverse process used by Schrödinger we can generate the Schrödinger equation by the information space and the continuity equation of the probability. In this way, the Hilbert mechanism can be explain only by information, curvature and probability.

3. A Hidden Variables Theory Does Not Meet the Existence of the Bloch Sphere

Assume that we have a set of N spins. Each of them is a spin-1/2 pure state lying in

the x-y plane. Let us assume that one source of N uncorrelated spin-carrying particles emits them in a state, which can be described as a multi spin-1/2 pure uncorrelated state. Let us parameterize the settings of the observer with a unit vector (its direction along which the spin component is measured) with. One can introduce the ‘hidden variables’ correlation function, which is the average of the product of the hidden results of measurement

(26)

where r is the hidden result. We assume the value of r is (in unit), which is obtained if the measurement directions are set at. We introduce ergodic averaging as a theoretical model here. We do not pursue the details of the assumption. To pursue the details is an interesting point. It is suitable to the next step of researches.

Also one can introduce a quantum correlation function with the system in such a pure uncorrelated state

(27)

where denotes the tensor product, ∙ the scalar product in, is a vector of two Pauli operators, and is the pure uncorrelated state,

(28)

with and is a spin-1/2 pure state lying in the x-y plane.

One can write the observable (unit) vector in a plane coordinate system as follows:

(29)

where and are the Cartesian axes. Here, the angle takes two values (two-setting model):

(30)

We derive a necessary condition to be satisfied by the quantum correlation function with the system in a pure uncorrelated state given in (27). In more detail, we derive the value of the product of the quantum correlation function, given in (27), i.e.,. We use the decomposition (29). We introduce simplified notations as

(31)

and

(32)

Then, we have

(33)

where we use the orthogonality relation. The value of is bounded as. We have

(34)

From the convex argument, all quantum separable states must satisfy the inequality (33). Therefore, it is a separability inequality. It is important that the separability inequality (33) is saturated iff is a multi spin-1/2 pure uncorrelated state such that, for every j, is a spin-1/2 pure state lying in the x − y plane. The reason of the inequality (33) is due to the existence of the Bloch sphere in quantum mechanics

(35)

The inequality (35) is saturated iff and is a spin-1/2 pure state lying in the x − y plane. The inequality (33) is saturated iff the inequality (35) is saturated for every j. Thus, we have the maximal possible value of the scalar product as a quantum proposition concerning the Bloch sphere

(36)

when the system is in such a multi spin-1/2 pure uncorrelated state.

3.1. Hidden Variables & Reference Frames

A hidden variables correlation function, assuming ergodicity, can be written as a weigthed sum over integer indices. For a function r in a function space we see e.g.

(37)

If a formulation with discrete indexing of hidden variables is a sensible way to describe a correlation, then one may select from a function such that

(38)

Here, the abbreviation is used. Instead of an index, real variables are employed. In addition we may assume that the function space contains a Heaviside type of function,

(39)

A sign function can then be obtained. Those sign functions are in and, hence, r can attain this form of sign function. The set in (38) is a subset of the interval

and has cardinality m. More explicitly,

The elements of can be shifted with an infinitesimal. This gives, , hence,

and.

3.2. Maximum Value and Product

We are very interested in the maximum value of the square of an expected value in a probability interpretation of quantum measurement theory. Therefore we focus on each measurement result providing a probability. And we study the maximum value when we inspect the summation. In short, we can multiply a measurement result by the same measurement result.

Therefore, we wish we would have some sort of Kronecker delta function at our disposal to match proper terms in the sum. In this respect it must be noted that the correlation in (38) can be arbitrary close approximated with the use of in the sum. We have, still using the “” symbol,

(40)

Assuming, , squaring the is in close approximation equal to the product of expressions in (38) and (40)

(41)

Because, of small differences, we may write in a Taylor like approximation,

The r product in (41) can then be re-written as

(42)

If the previous result from (42) is introduced in (41) then the latter can be re-written as

If for a sign form is employed based on (39), then it is easy to see that for proper, the following

will be true. The form contains, numerically and in limit, something

similar to because r is a sign. We can conclude that given r is a sign function based on (39), it is plausible to expect for proper we obtain

(43)

for.

3.3. Quantum and hv Values

We study the possibility,. For the ease of the presentation we write, and suppress the notation. Hence, from our previous considerations we then write, under the limit, and employing the result in (43)

(44)

We use the following fact

(45)

for properly selected. Hence, one has the following proposition concerning the hidden variables theory

(46)

Clearly, we cannot assign the truth value “1’’ for two propositions (36) (concerning the Bloch sphere) and (46) (concerning the hidden variables theory), simultaneously, when the system is in a multiparticle pure uncorrelated state. Of course we can imagine where this would be possible but the hv theory would be in need of a sufficient number of special points in the that makes the r vanish for all. In general, the claim can be made that the selection of hv theories is not as free as one would prefer.

To continue we note, each of the theories refers to a spin-1/2 pure state lying in the x-y plane. Therefore, we are in the contradiction when the system is in such a multiparticle pure uncorrelated state. Thus, we cannot accept a general validity of the proposition of a hidden variables theory, if we assign the truth value “1’’ for the proposition (36) (concerning the Bloch sphere).

4. Conclusion and Discussions

In conclusion, we have studied the relation between a hidden variables theory and the existence of the Bloch sphere and with a new type of conditional probability and Fisher information as metric for information space we show that the hidden variable are not possible. Now, we have derived some proposition concerning a quantum expected value under an assumption about the existence of the Bloch sphere in N spin-1/2 systems. However, the hidden variables theory has violated the proposition with a magnitude that grows exponential with the number of particles. Therefore, we have had to give up either the existence of the Bloch sphere or the hidden variables theory. The hidden variables theory does not have depictured physical phenomena using the existence of the Bloch sphere with a violation factor that grows exponentially with the number of particles. Now, we point out the problem that when we cannot measure an observable we cannot say nothing on this measure as in the non-commutative case. So we have contradictions. In classical interpretation of quantum mechanics does not exist conditional probability and we cannot measure the probability but with the introduction of the information space and Fisher metric we show that conditional probability is possible but limited to statistical parameters as average value or other parameters. So contradiction is eliminated. Now, entanglement and Bell theorem can be understood in a new type of set theory that includes copula [27] and information [28] . Maybe we are right that projection operator is not sufficient to understand quantum mechanics so we cannot give Hilbert space axiomatic structure. Now, axiomatic Hilbert space is useful but cannot completely explain the meaning of the quantum mechanics. With information space, we can give a meaning with the axiomatic Hilbert that is always a useful mathematical instrument to use information and probability together.

Cite this paper

Nagata, K., Resconi, G., Nakamura, T. and Geurdes, H. (2016) Information and Conditional Probability to Go beyond Hidden Variables. Journal of Applied Mathematics and Physics, 4, 2203- 2214. http://dx.doi.org/10.4236/jamp.2016.412214

References