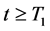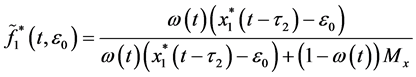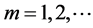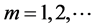Journal of Applied Mathematics and Physics
Vol.04 No.03(2016), Article ID:65107,15 pages
10.4236/jamp.2016.43060
Permanence, Periodicity and Extinction of a Delayed Biological System with Stage-Structured Preference for Predator
Limin Zhang1,2*, Chaofeng Zhang1
1School of Mathematics and Finance-Economics, Sichuan University of Arts and Science, Dazhou, China
2School of Mathematics, Sichuan University, Chengdu, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 January 2016; accepted 26 March 2016; published 29 March 2016
ABSTRACT
This study considers a delayed biological system of predator-prey interactions where the predator has stage-structured preference. It is assumed that the prey population has two stages: immature and mature. The predator population has different preference for the stage-structured prey. This type of behavior has been reported in Asecodes hispinarum and Microplitis mediator. By some lemmas and methods of delay differential equation, the conditions for the permanence, existence of positive periodic solution and extinction of the system are obtained. Numerical simulations are presented that illustrate the analytical results as well as demonstrate certain biological phenomena. In particular, overcrowding of the predator does not affect the persistence of the system, but our numerical simulations suggest that overcrowding reduces the density of the predator. Under the assumption that immature prey is easier to capture, our simulations suggest that the predator’s preference for immature prey increases the predator density.
Keywords:
Stage-Structured Preference, Permanence, Periodic Solution, Extinction, Time Delay

1. Introduction
In recent years, much attention has been paid to biological systems with stage structure [1] - [23] . One important reason is that there are many species whose individual members have a life history taking them through two stages, immature and mature. Thus considering stage structure in population corresponds with the natural phenomenon. Another reason is that stage-structured ecological models are much simpler than the models governed by partial differential equations but they can exhibit phenomena similar to those of partial differential equations and many important physiological parameters can be incorporated [24] . The other reason is that the biological dynamics has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance [25] .
In References [1] - [5] , the authors have studied the stability of a class of stage-structured predator-prey systems. The authors in [6] [7] have made Hopf bifurcation analysis in delayed predator-prey systems with stage structure. As we know, environmental and biological parameters (such as the seasonal effects of weather, food supplies, and mating habits) fluctuate naturally over time; thus the effects of periodically varying environments are considered to be important selective forces in systems with fluctuating environments [19] [20] . Thus, incorporating periodicity into models of stage-structured biological systems is more realistic with a changing environment. Therefore, many researchers have studied a class of periodic nonautonomous biological systems with stage structures [8] - [16] [21] . Recently, Cui and Song [21] considered the following predator-prey system with stage-structured prey:
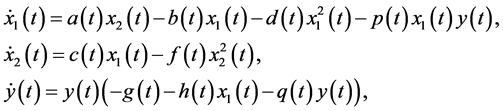 (1.1)
(1.1)
where ,
, 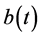 ,
,  ,
, 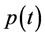 ,
, 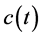 ,
, 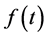 ,
,  ,
, 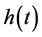 and
and 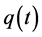 are all continuous positive T-periodic functions, and
are all continuous positive T-periodic functions, and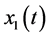 ,
,  , and
, and  denote the densities of immature prey, mature prey, and predator species, respectively. They obtained a set of sufficient and necessary conditions that guarantee the permanence of the system.
denote the densities of immature prey, mature prey, and predator species, respectively. They obtained a set of sufficient and necessary conditions that guarantee the permanence of the system.
In the natural world, many predators switch to alternative prey when their favored food is in short supply [22] - [24] . For example, the lynx switches to red squirrel when the snowshoe hare is scarce [25] . Even if there is only one prey type, the degree of predation or the quality (including palatability) of prey is likely to vary with its stage structure, which is likely to affect the predator’s preference for different stage-structured prey. This type of behavior has been reported in Asecodes hispinarum [26] , who parasitizes all 5 instars of Brontispa Logissina, but prefers to parasitize the 2nd and 3rd instars when it is exposed to all the instars of larvae, and in Microplitis mediator [27] , who prefers to parasitize the 2nd and 3rd instars of Mythimna separate.
However, previous studies on prey age preference only have been done in laboratory tests. Few researchers have investigated the phenomenon with mathematical models and carried out theoretical analysis together with numerical simulation. To extend research in this area, and based on the recent study by Cui and Song [21] , we consider a periodic predator-prey system with time delay and a predator with stage-structured preference.
2. Formulation of the Model
Let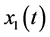 ,
, 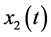 and
and 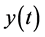

where
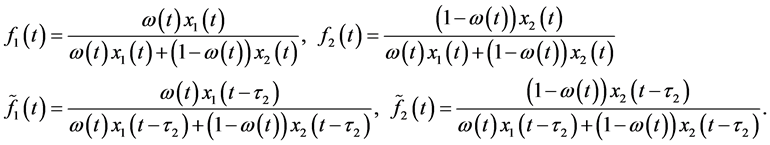
The coefficients in system (2.1) are all continuous positive T-periodic functions. Parameter 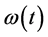
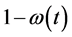
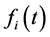

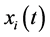

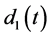
The term 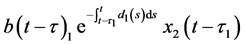
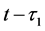
survive, and those progressing from the immature stage to the mature stage at time t. The death rate of the mature prey population is logistic in nature and it is proportional to the square of the population with proportionality


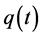
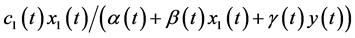

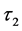


The initial conditions for system (2.1) take the form of
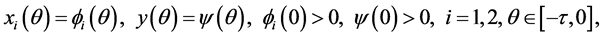
where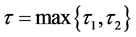
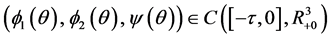
mapping the interval 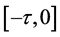
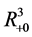
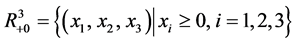
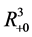
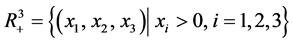
For continuity of initial conditions, we require
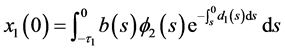
For the purpose of convenience, we write

Obviously, 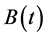
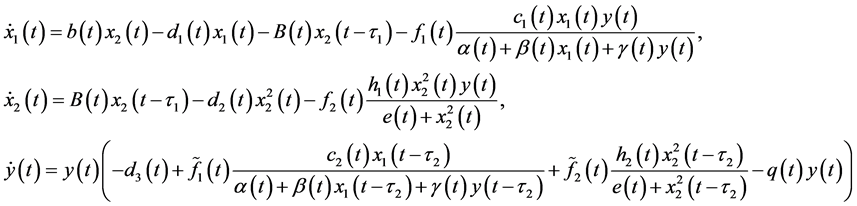
In this paper, we consider system (2.5) with initial conditions (2.3) and (2.4). At the same time, we adopt the following notation through this paper:
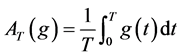
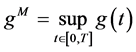
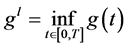
where 
The rest of the paper is arranged as follows. In the following section, we introduce some lemmas and then explore the permanence and periodicity of system (2.5). In Section 4, we investigate the extinction of the predator population in system (2.5). In Section 5, numerical simulations are presented to illustrate the feasibility of our main results. Furthermore, the simulated results are explained according to the biological perspective. In section 6, a brief discussion is given to conclude this work.
3. Permanence and Periodicity
In this section, we analyze the permanence and periodicity of system (2.5) with initial conditions (2.3) and (2.4). Firstly, we introduce the following definition and Lemmas which are useful to obtain our result.
Definition 3.1. The system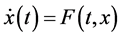
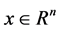
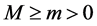
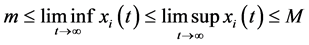
Lemma 3.2. (See [30] ). If 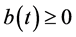
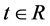
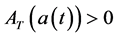
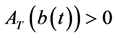
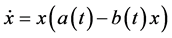
has a unique positive T-periodic solution which is globally asymptotically stable.
Lemma 3.3. (See [31] ). System

has a unique positive T-periodic solution 

Lemma 3.4. There exists a positive constant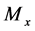

for all the solution of system (3.2) with respect to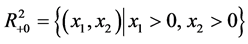
Proof. Let 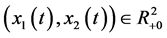
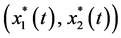
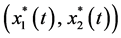

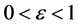

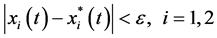
By applying (3.4), we obtain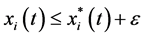
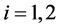
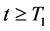
Let
We have

Theorem 3.5. System (2.5) is permanent and has at least one positive T-periodic solution provided
where

where 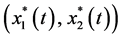

We need the following propositions to prove Theorem 3.5.
Proposition 3.6. For all the solutions of system (2.5) with initial conditions (2.3) and (2.4), we have

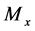
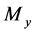
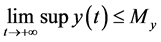
Proof. Obviously, 

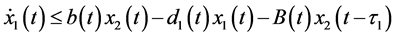
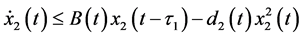
Consider the following auxiliary system
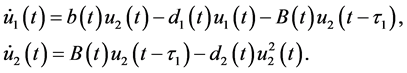
By Lemma 3.3, system (3.7) has a unique globally attractive positive T-periodic solution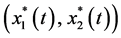



By applying (3.8) and Lemma 3.4, we obtain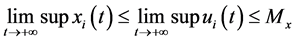
In addition, from the third equation of (2.5) we have

Consider the following auxiliary equation:
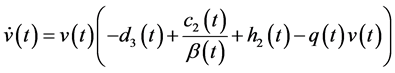
According to the condition (3.6), we have
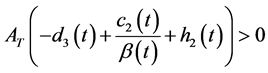
By (3.10) and Lemma (3.2), we obtain that system (3.9) has a unique positive T-periodic solution 

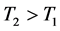
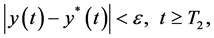
By applying (3.11), we obtain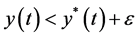

Set

This completes the proof of Proposition 3.6. □
Proposition 3.7. There exists a positive constant
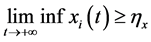
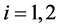
Proof. By Proposition 3.6, there exists a positive 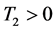
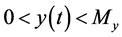
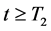
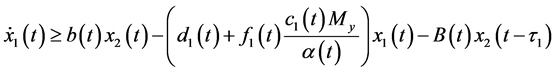
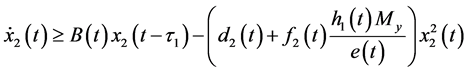
for
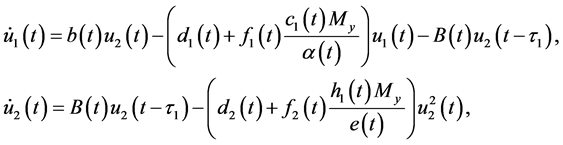
has a unique global attractive positive T-periodic solution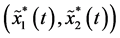
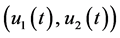
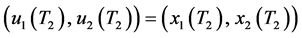
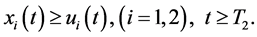
Moreover, from the global attractivity of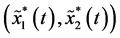
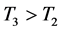
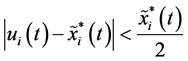
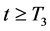
Combined (3.14) with (3.15), we have
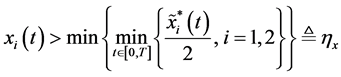

Therefore, 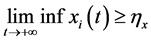

Proposition 3.8. Suppose that (3.6) holds, then there exists a positive constant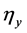


Proof. By assumption (3.6), we can choose arbitrarily small constant 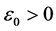
assume that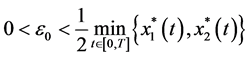
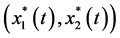
system (3.2)), such that
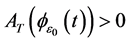
where
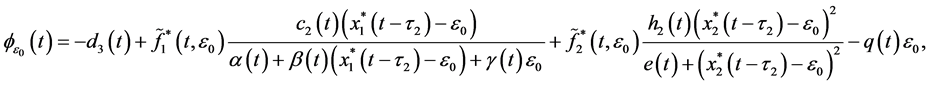

Consider the following system with a parameter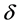
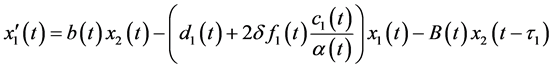

By Lemma 3.3, system (3.19) has a unique positive T-periodic solution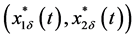
attractive. Let 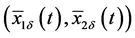
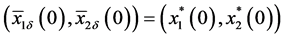
Then, for the above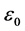
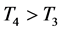
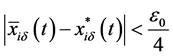

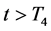
Using the continuity of the solution in the parameter, we have 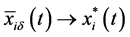
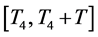
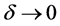
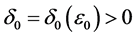
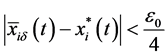

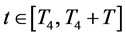
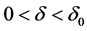
So, we get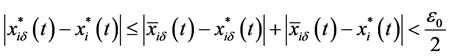
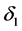

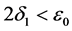

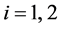
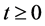
Suppose that the conclusion (3.17) is not true, then there exists 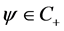
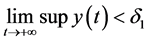
where 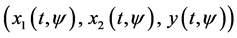

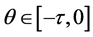
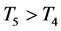
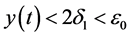
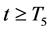
By applying (3.21), from the first and second equation of system (2.5), we have
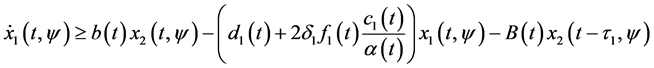
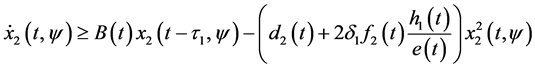
for all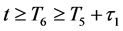
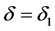
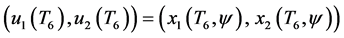
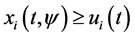
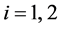
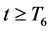
asymptotic stability of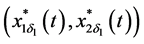
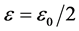

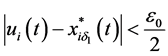

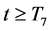
So,

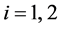

By using (3.20), we obtain
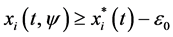

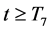
Therefore, by using (3.21) and (3.22), for 
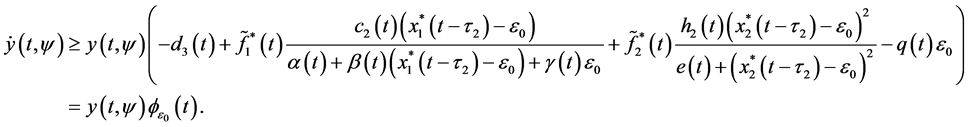
Integrating (3.23) from 
Thus, from (3.18) we know that 
Proposition 3.9. Suppose that (3.6) holds, then there exists a positive constant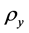
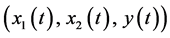
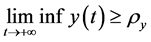
Proof. Suppose that (3.24) is not true, then there exists a sequence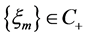

On the other hand, by Proposition 3.8, we have

Hence, there exist time sequences 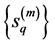
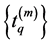
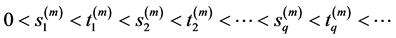
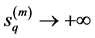
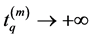
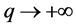
and
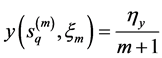
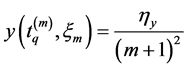
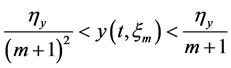
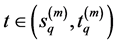
By Proposition 3.6, for a given positive integer m, there exist a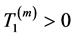
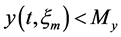
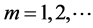
Because of 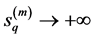

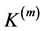
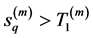
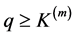
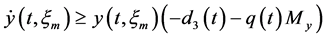
for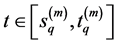
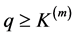
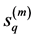
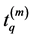
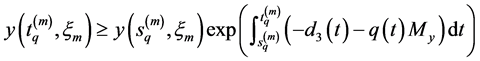
or
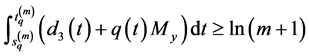
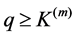
Thus, from the boundedness of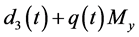



By (3.18) and (3.27), there exist constants 

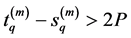
and 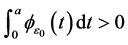
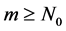
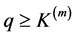
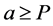
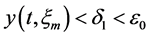
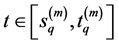
for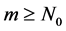
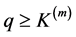
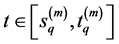

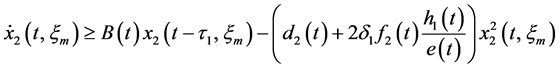
Let 

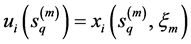
comparison theorem, we have
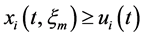
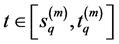
By using Propositions 3.6 and 3.7, there exists a large enough 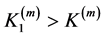
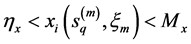
for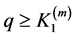
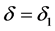
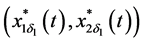
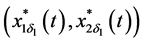
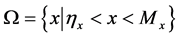
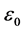


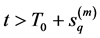
Therefore, by using (3.20),

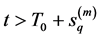
According to (3.27), there exists a positive integer 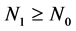
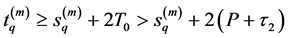
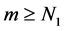
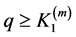
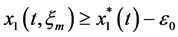
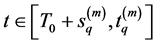
as 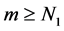

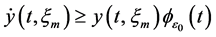
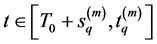
Integrating (3.31) from 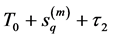
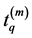
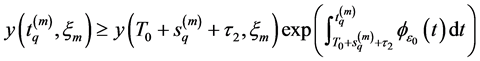
that is,
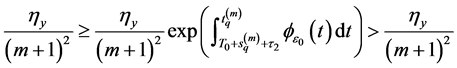
This is a contradiction. This completes the proof of Proposition 3.9. □
Proof of Theorem 3.5. By using Propositions 3.6-3.9, system (2.5) is permanent. Using result given by Teng and Chen in [33] , we obtain system (2.5) has at least one positive T-periodic solution. This completes the proof of Theorem 3.5.
4. Extinction
In this section, we investigate the extinction of the predator population in system (2.5) with initial conditions (2.3) and (2.4) under some condition.
Theorem 4.1. Suppose that
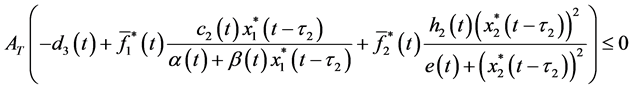
where

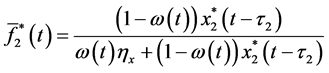
where 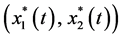
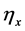
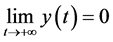
Proof. According to (4.1), for every given positive constant 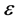
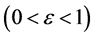
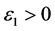
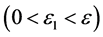
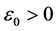
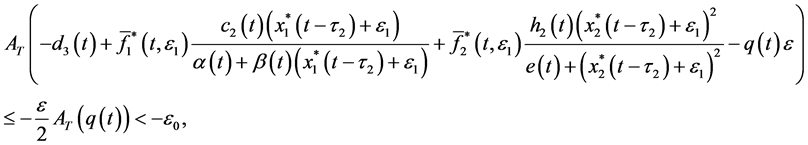
where
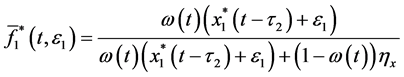
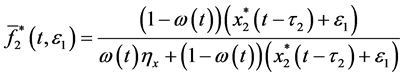
From the first and second equations of system (2.5), we have
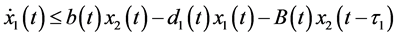
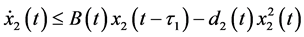
Hence, for the above 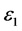
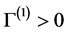
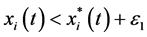
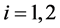
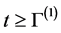
It follows from (4.2) and (4.3) that for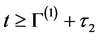
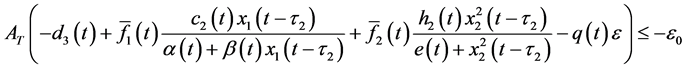
Firstly, we show that exists a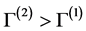

That is to say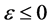
Secondly, we show that
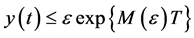
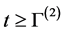
where
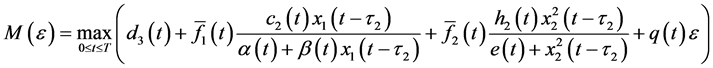
is bounded for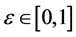
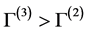
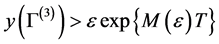
By the continuity of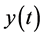
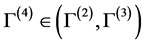
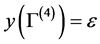
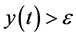

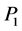
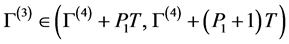
(4.3), we have
which is a contradiction. This shows that (4.5) holds. By the arbitrariness of

5. Examples
In this section, we give some examples to illustrate the feasibility of our main results in Theorems 3.5 and 4.1.
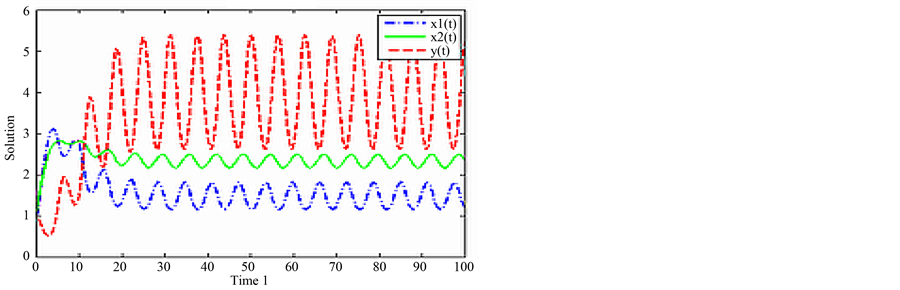
Example 5.1. Let

In this case, system (3.2) given by Lemma 3.3 has a unique positive periodic solution
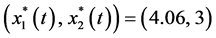

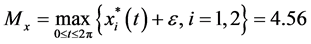
calculation, we have
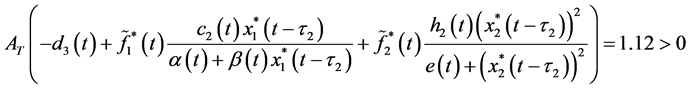
According to Theorem 3.5, system (2.5) with the above coefficients is permanent and admits at least one positive 2p-periodic solution for any nonnegative 2p-periodic function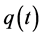
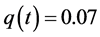
Figure 1. The periodic solution found by numerical integration of system (2.5) with initial condition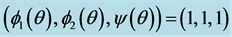
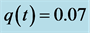
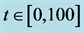

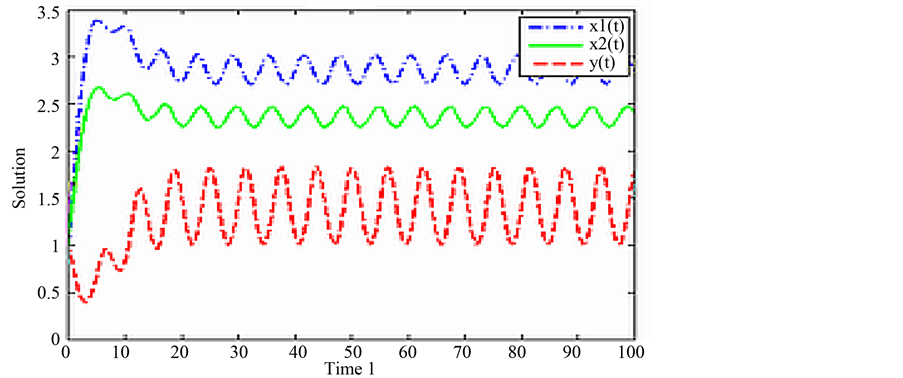
Figure 2. The periodic solution found by numerical integration of system (2.5) with initial condition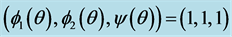



(2.5) with the above coefficients and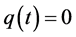
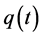
Example 5.2. In system (2.5), let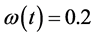
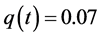
Example 5.3. In system (2.5), let
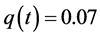

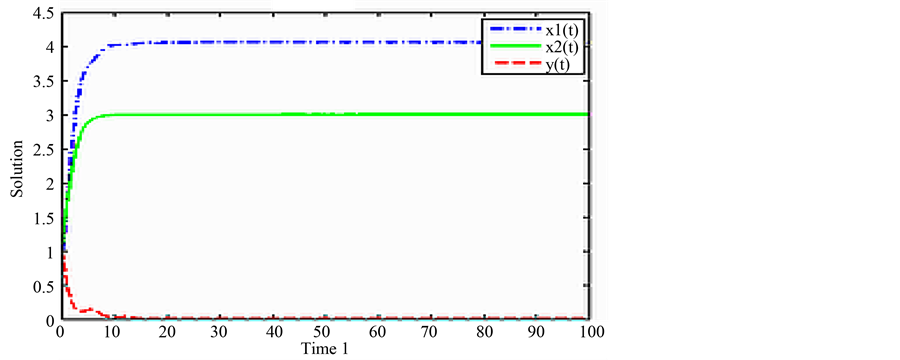
According to Theorem 4.1, system (2.5) is impermanent and the predator population is extinction. Numerical simulation given in Figure 4 also confirms the result.
6. Conclusions
In this paper, we propose and analyze a periodic predator-prey system with time delay and prey stage-structured preference by the predator. The permanence and existence of positive periodic solutions of system (2.5) are explored. The conditions for the impermanence of the system and the extinction of the predator population are obtained. By Lemma 3.3, we know that 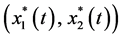
Figure 3. The periodic solution found by numerical integration of system (2.5) with initial condition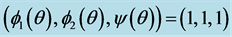
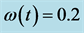


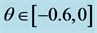
Figure 4. The temporal solution found by numerical integration of system (2.5) with initial condition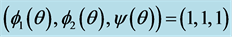

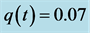

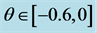
more palatable and more easily captured by the predator than the mature. Example 5.3 illustrates the correctness of Theorem 4.1.
We would like to mention here that we are unable to solve the following questions:
1) How many positive periodic solutions exist in system (2.5)?
2) Is the solution global attractivity if system (2.5) has only one positive periodic solution?
We leave these for future work.
Acknowledgements
The authors express sincere gratitude to the anonymous referees for their helpful comments and suggestions that led to an improvement of our original manuscript.
Funding
This work was supported by the Major Project of Sichuan University of Arts and Science (Grant No. 2014Z005Z), by the General Project of Educational Commission in Sichuan Province (Grant No. 16ZB0357).
Cite this paper
Limin Zhang,Chaofeng Zhang, (2016) Permanence, Periodicity and Extinction of a Delayed Biological System with Stage-Structured Preference for Predator. Journal of Applied Mathematics and Physics,04,546-560. doi: 10.4236/jamp.2016.43060
References
- 1. Falconi, M., Huenchucona, M. and Vidal, C. (2015) Stability and Global Dynamic of a Stage-Structured Predator-Prey Model with Group Defense Mechanism. Applied Mathematics and Computation, 270, 47-61.
http://dx.doi.org/10.1016/j.amc.2015.07.109 - 2. Fawzi, J. and Omari, M. (2015) The Effect of State Dependent Delay and Harvesting on a Stage-Structured Predator-Prey Model. Applied Mathematics and Computation, 271, 142-153.
http://dx.doi.org/10.1016/j.amc.2015.08.119 - 3. Meng, X.-Y., Huo, H.-F., Xiang, H. and Yin, Q.-Y. (2014) Stability in a Predator-Prey Model with Crowley-Martin Function and Stage Structure for Prey. Applied Mathematics and Computation, 232, 810-819.
http://dx.doi.org/10.1016/j.amc.2014.01.139 - 4. Liu, C., Zhang, Q.-L. and Huang, J. (2013) Stability Analysis of a Harvested Prey-Predator Model with Stage Structure and Maturation Delay. Mathematical Problems in Engineering, 2013, Article ID: 329592.
http://dx.doi.org/10.1155/2013/329592 - 5. Xu, R., Chaplain, M. and Davidson, F. (2004) Persistence and Global Stability of a Ratio-Dependent Predator-Prey Model with Stage Structure. Applied Mathematics and Computation, 158, 729-744.
http://dx.doi.org/10.1016/j.amc.2003.10.012 - 6. Deng, L.-W., Wang, X.-D. and Peng, M. (2014) Hopf Bifurcation Analysis for a Ratio-Dependent Predator-Prey System with Two Delays and Stage Structure for the Predator. Applied Mathematics and Computation, 231, 214-230.
http://dx.doi.org/10.1016/j.amc.2014.01.025 - 7. Qu, Y. and Wei, J. (2010) Bifurcation Analysis in a Predator-Prey System with Stage-Structure and Harvesting. Journal of the Franklin Institute, 347, 1097-1113.
http://dx.doi.org/10.1016/j.jfranklin.2010.03.017 - 8. Ma, Z., Wang, S., Wang, W. and Li, Z. (2011) Permanence of a Stage-Structured Predator-Prey System with a Class of Functional Responses. Comptes Rendus Biologies, 334, 851-854.
http://dx.doi.org/10.1016/j.crvi.2011.08.002 - 9. Zhang, L.-M. and Zhang, C.-F. (2010) Rich Dynamic of a Stage-Structured Prey-Predator Model with Cannibalism and Periodic Attacking Rate. Communications in Nonlinear Science and Numerical Simulation, 15, 4029-4040.
http://dx.doi.org/10.1016/j.cnsns.2010.02.009 - 10. Zhang, Z.-Q. and Luo, J. (2010) Multiple Periodic Solutions of a Delayed Predator-Prey System with Stage Structure for the Predator. Nonlinear Analysis: Real World Applications, 11, 4109-4120.
http://dx.doi.org/10.1016/j.nonrwa.2010.03.015 - 11. Nie, L., Teng, Z., Hu, L. and Peng, J. (2009) Existence and Stability of Periodic Solution of a Predator-Prey Model with State-Dependent Impulsive Effects. Mathematics and Computers in Simulation, 79, 2122-2134.
http://dx.doi.org/10.1016/j.matcom.2008.11.015 - 12. Kouche, M., Tatar, N.E. and Liu, S. (2008) Permanence and Existence of a Positive Periodic Solution to a Periodic Stage-Structured System with Infinite Delay. Applied Mathematics and Computation, 202, 620-638.
http://dx.doi.org/10.1016/j.amc.2008.03.002 - 13. Chen, F. and You, M. (2008) Permanence, Extinction and Periodic Solution of the Predator-Prey System with Beddington-DeAngelis Functional Response and Stage Structure for Prey. Nonlinear Analysis: Real World Applications, 9, 207-221.
http://dx.doi.org/10.1016/j.nonrwa.2006.09.009 - 14. Xia, Y., Cao, J. and Cheng, S. (2007) Multiple Periodic Solutions of a Delayed Stage-Structured Predator-Prey Model with Non-Monotone Functional Responses. Applied Mathematical Modelling, 31, 1947-1959.
http://dx.doi.org/10.1016/j.apm.2006.08.012 - 15. Chen, F.D. (2006) Permanence of Periodic Holling Type Predator-Prey System with Stage Structure for Prey. Applied Mathematics and Computation, 182, 1849-1086.
http://dx.doi.org/10.1016/j.amc.2006.06.024 - 16. Xu, R., Chaplain, M.-A.-J. and Davidson, F.A. (2005) Permanence and Periodicity of a Delayed Ratio-Dependent Predator-Prey Model with Stage Structure. Journal of Computational and Applied Mathematics, 303, 602-621.
- 17. Bence, J.-R. and Nisbet, R.-M. (1989) Space Limited Recruitment in Open Systems: The Importance of Time Delays. Ecology, 70, 1434-1441.
http://dx.doi.org/10.2307/1938202 - 18. Berryman, A.-A. (1992) The Origins and Evolution of Predator-Prey Theory. Ecology, 75, 1530-1535.
http://dx.doi.org/10.2307/1940005 - 19. Cushing, J.-M. (1977) Periodic Time Dependent Predator-Prey System. SIAM Journal on Applied Mathematics, 32, 82-95.
http://dx.doi.org/10.1137/0132006 - 20. Krukonis, G. and Schaffer, W.-M. (1991) Population Cycles in Mammals and Birds: Does Periodicity Scale with Body Size? Journal of Theoretical Biology, 148, 469-493.
http://dx.doi.org/10.1016/S0022-5193(05)80232-2 - 21. Cui, J.-A. and Song, X.-Y. (2004) Permanence of a Predator-Prey System with Stage Structure. Discrete Continuous Dynamic Systems-Series B, 4, 547-554.
http://dx.doi.org/10.3934/dcdsb.2004.4.547 - 22. Provost, C., Lucas, E. and Coderre, D. (2006) Prey Preference of Hyaliodes vitripennis as an Intraguild Predator: Active Predator Choice or Passive Selection? Biological Control, 37, 148-154.
http://dx.doi.org/10.1016/j.biocontrol.2006.01.005 - 23. Baalen, M., Krivan, V., van Rijn, P.-C. and Sabelis, M.-W. (2001) Alternative Food, Switching Predators, and the Persistence of Predator-Prey Systems. American Nature, 157, 512-524.
http://dx.doi.org/10.1086/319933 - 24. Goldman, J.-C. and Dennett, M.-R. (1990) Dynamics of Prey Selection by an Omnivorous Flagellate. Marine Ecology Progress Series, 59, 183-194.
http://dx.doi.org/10.3354/meps059183 - 25. O’Donoghue, M., Boutin, S., Krebs, C.-J., Zuleta, G. and Dennis, L. (1998) Functional Response of Coyotes and Lynx to the Snowshoe Hare Cycle. Ecology, 79, 1193-1208.
http://dx.doi.org/10.2307/176736 - 26. Chao, T., Peng, Z.-Q., Shen, Y.-X., Lu, B.-Q., Fu, Y.-G. and Wang, F.-G. (2006) Host Age Preference and Suitability of Asecodes hispinarum. Chinese Journal of Tropical Crops, 27, 78-80. (In Chinese)
- 27. Li, J., Coudron, T.-A., Pan, W., Liu, X., Lu, Z. and Zhang, Q. (2006) Host Age Preference of Microplitis mediator (Hymenoptera: Braconidae), an Endoparasitoid of Mythimna separata (Lepidoptera: Noctuidae). Biological Control, 39, 257-261.
http://dx.doi.org/10.1016/j.biocontrol.2006.09.002 - 28. Venzon, M., Jansse, A. and Sabelis, M.-W. (2001) Prey Preference, Intraguild Predation and Population Dynamics of an Arthropod Food Web on Plants. Experimental and Applied Acarology, 25, 785-808.
http://dx.doi.org/10.1023/A:1020443401985 - 29. Rai, V., Anand, M. and Upadhyay, R.-K. (2007) Trophic Structure and Dynamical Complexity in Simple Ecological Models. Ecological Complexity, 4, 212-222.
http://dx.doi.org/10.1016/j.ecocom.2007.06.010 - 30. Zhao, X.-Q. (1991) The Qualitative Analysis of N-Species Lotka-Volterra Periodic Competition Systems. Mathematical and Computer Modelling, 15, 3-8.
http://dx.doi.org/10.1016/0895-7177(91)90100-L - 31. Liu, S.-Q., Chen, L.-S. and Liu, Z.-J. (2002) Extinction and Permanence in Nonautonomous Competitive System with Stage Structure. Journal of Mathematical Analysis and Applications, 274, 667-684.
http://dx.doi.org/10.1016/S0022-247X(02)00329-3 - 32. Lakshmikantham, V., Matrosov, V.-M. and Sivasundaram, S. (1991) Vector Lyapunov Functions and Stability Analysis of Nonlinear Systems. Vol. 63, Kluwer Academic Publishers, Dordrecht, Boston, London.
http://dx.doi.org/10.1007/978-94-015-7939-1 - 33. Teng, Z. and Chen, L. (1999) The Positive Periodic Solutions in Periodic Kolmogorov Type Systems with Delays. Acta Mathematicae Applicatae Sinica, 22, 446-456.
- 34. Rai, V., Anand, M. and Upadhyay, R.K. (2007) Trophic Structure and Dynamical Complexity in Simple Ecological Models. Ecological Complexity, 4, 212-222.
http://dx.doi.org/10.1016/j.ecocom.2007.06.010
NOTES
*Corresponding author.