Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63769,7 pages
10.4236/jamp.2016.42035
Riemannian Acceleration in Oblate Spheroidal Coordinate System
N. E. J. Omaghali1, S. X. K. Howusu2
1Department of Physics, University of Jos, Jos, Nigeria
2Theoretical Physics Program, National Mathematical Centre, Abuja, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2015; accepted 22 February 2016; accepted 25 February 2016
ABSTRACT
The planetary bodies are more of a spheroid than they are a sphere thereby making it necessary to describe motions in a spheroidal coordinate system. Using the oblate spheroidal coordinate sys- tem, a more approximate and realistic description of motion in these bodies can be realized. In this paper, we derive the Riemannian acceleration for motion in oblate spheroidal coordinate system using the golden metric tensor in oblate spheroidal coordinates. The Riemannian accele- ration in the oblate spheroidal coordinate system reduces to the pure Newtonian acceleration in the limit of c0 and contains post-Newtonian correction terms of all orders of c−2. The result ob- tained thereby opens the way for further studies and applications of the motion of particles in ob- late spheroidal coordinate system.
Keywords:
Riemannian Acceleration, Golden Metric Tensor, Oblate Spheroidal Coordinates, Christoffel’s Symbols

1. Introduction
Most planetary bodies have been assumed to be spherical and consequently, many treatments of motion involving these bodies have been taken into consideration the spherical approximation of the bodies [1] - [3] . However, despite the spherical assumption of planetary bodies, studies have shown that the oblate spheroid is a more approximate description of these bodies [4] - [7] , thus the need for a description of the planetary bodies in terms of the oblate spheroidal coordinate system.
It is worth noting that the description of the planetary bodies mentioned so far have been based on the theory of orthogonal curvilinear coordinates [8] and with foundations on the Euclidean Geometry. However, following the presentation of the work of Riemann in 1854 which laid the foundations for the Riemannian Geometry, there had been considerable interest in the Riemannian Geometry. Consequently, in this paper, we employ the Metric Tensors in oblate spheroidal coordinate system [9] to derive the Riemannian acceleration for the oblate spheroidal coordinate system.
2. Mathematical Formulation
2.1. Oblate Spheroidal Coordinate
In this formulation we have chosen the spheroidal coordinate system based on the approximate representation of the planetary bodies as oblate spheroids. The surface generated by the rotation of an ellipse about its minor axis
is an oblate spheroid. The oblate spheroidal coordinate system  is related to the Cartesian coordinate system
is related to the Cartesian coordinate system 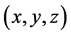 as follows:
as follows:
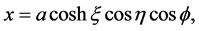 (1)
(1)
 (2)
(2)
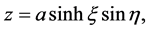 (3)
(3)
where a is the ellipse’s focal distance and this distance is one-half the ellipse’s foci such that
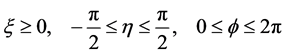 (4)
(4)
Therefore, the differential length of a line element  in the oblate spheroidal coordinates
in the oblate spheroidal coordinates  is obtained from
is obtained from
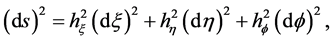 (5)
(5)
where 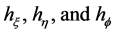 are the scale factors for the
are the scale factors for the 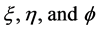 coordinates respectively. Hence, from the theory of orthogonal coordinates [8] [10] , we can write the scale factors explicitly as
coordinates respectively. Hence, from the theory of orthogonal coordinates [8] [10] , we can write the scale factors explicitly as
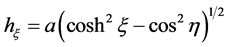 (6)
(6)
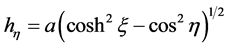 (7)
(7)
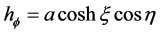 (8)
(8)
Following from Equations (1)-(3), we can define the space time position tensor in oblate spheroidal coordinate system as the set of four labelled quantity  as:
as:

Equation (9) can be written explicitly in terms of the coordinate axes as

and in Einstein’s coordinates 
2.2. Metric Tensor
A fundamental quantity in Riemannian coordinate geometry is the metric tensors. Therefore the metric tensor in the oblate spheroidal coordinate system is necessary for the formulation of the Riemannian acceleration in the spheroidal coordinate system. Thus the golden metric tensor in the oblate spheroidal coordinates, 





where

is the gravitational scalar potential. From Equations (11)-(15) we can obtain the corresponding contravariant metric tensors, 





3. Acceleration
With the metric tensors in Equations (11)-(15) and Equations (17)-(21), we can proceed to define another quantity which depends on the metric tensors. This quantity is the Christoffel’s symbols of the second kind or the coefficient of affine connections. The coefficient of affine connection or Christoffels’s symbol of the second kind is the set of labelled quantities, 

Thus, using Equation (22), and with the metric tensors given by Equations (11)-(15) and Equations (17)-(21), we can obtain all the nonzero terms of the coefficient of affine connections. Hence, after some mathematical simplification, the non-zero terms of Equation (22) is obtained as follows:







and







and







and







and

Therefore, the equations given by (23)-(51) denote all the coefficients of affine connection or Christoffel’s symbols of the second kind, where for example, 


The first rank tensor, 

is called the Riemannian space-time or 4-dimensional “linear acceleration” tensor; 



where




The Equations (54)-(57) are the physically measurable four dimensional acceleration components along the corresponding coordinate axes 
Now, substituting Equations (23)-(51) into Equation (52) and after some mathematical simplification, we can then write Equations (54)-(57) explicitly.
Consequently, Equation (54) for 

Equation (55) for 

Equation (56) for 

and Equation (57) for 

where 

4. Results and Discussion
In this paper, we have derived the Riemannian acceleration for the oblate spheroidal coordinate system
Newtonian linear acceleration in the limit of

Cite this paper
N. E. J.Omaghali,S. X. K.Howusu, (2016) Riemannian Acceleration in Oblate Spheroidal Coordinate System. Journal of Applied Mathematics and Physics,04,279-285. doi: 10.4236/jamp.2016.42035
References
- 1. Howusu, S.X.K. (2004) Gravitational Fields of Spheroidal Bodies-Extension of Gravitational Fields of Spherical Bodies. Galilean Electrodynamics, 16, 97-100.
- 2. Liang, Q., Chen, C. and Li, Y. (2014) 3-D Inversion of Gravity Data in Spherical Coordinates with Application to the GRAIL Data. Journal of Geophysical Research: Planets, 119, 1359-1373.
http://dx.doi.org/10.1002/2014je004626 - 3. Lomax, A.J. and Michelini, A. (1988) The Use of Spherical Coordinates in the Interpretation of Seismograms. Geophysical Journal International, 93, 405-412.
http://dx.doi.org/10.1111/j.1365-246X.1988.tb03868.x - 4. Vinti, J.P. (1960) New Approach in the Theory of Satellite Orbits. Physical Review Letters, 3, 8.
http://dx.doi.org/10.1103/PhysRevLett.3.8 - 5. Vinti, J.P. (1966) Invariant Properties of the Spheroidal Potential of an Oblate Planet. Journal of Research of the National Bureau of Standards, 70B, 1-6.
http://dx.doi.org/10.6028/jres.070B.002 - 6. Gates, W.L. (2004) Derivation of the Equations of Atmospheric Motion in Oblate Spheroidal Coordinates. Journal of the Atmospheric Science, 61, 2478-2487.
http://dx.doi.org/10.1175/1520-0469(2004)061<2478:DOTEOA>2.0.CO;2 - 7. Goldreich, P. (1965) Inclination of Satellite Orbits about an Oblate Processing Planet. The Astronomical Journal, 70, 5-9.
http://dx.doi.org/10.1086/109673 - 8. Morse, P.M. and Feshbach, H. (1953) Methods of Theoretical Physics. McGraw-Hill, New York.
- 9. Howusu, S.X.K. (2013) Riemannian Revolutions in Physics and Mathematics. Jos University Press Ltd., Jos.
- 10. Arfken, G. (1985) Mathematical Methods for Physicists. Academic Press, Orlando.
- 11. Spiegel, M.R. (1974) Theory and Problems of Vector Analysis and Introduction to Tensor Analysis. MC Graw-Hill, New York.

