Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61349,6 pages
10.4236/jamp.2015.311168
The Asymptotic Iteration Method for the Eigenenergies of the a Novel Hyperbolic Single Wave Potential
Abdallah J. Sous
Al-Quds Open University, Tulkarm, Palestine

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 October 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT
By using the asymptotic iteration method, we have calculated numerically the eigenvalues  of the hyperbolic single wave potential
of the hyperbolic single wave potential 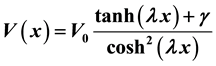 which is introduced by H. Bahlouli, and A. D. Alhaidari. They found a new approach (the “potential parameter” approach) which has been adopted for this eigenvalues problem. For a fixed energy, the problem is solvable for a set of values of the potential parameters (the “parameter spectrum”). This paper will introduce a related work to complete the goal of finding the eigenvalues, the Schrödinger equation with hyperbolic single wave potential is solved by using asymptotic iteration method. It is found that asymptotically this method gives accurate results for arbitrary parameters
which is introduced by H. Bahlouli, and A. D. Alhaidari. They found a new approach (the “potential parameter” approach) which has been adopted for this eigenvalues problem. For a fixed energy, the problem is solvable for a set of values of the potential parameters (the “parameter spectrum”). This paper will introduce a related work to complete the goal of finding the eigenvalues, the Schrödinger equation with hyperbolic single wave potential is solved by using asymptotic iteration method. It is found that asymptotically this method gives accurate results for arbitrary parameters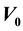 ,
, 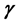 , and
, and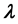 .
.
Keywords:
Schrodinger Equation, Asymptotic Iteration Method, The Hyperbolic Single Wave Potential, Numerical Eigenenergies

1. Introduction
The numerical solutions of the Schrödinger equation have taken a great deal of interest in the description of nuclear motion in molecules in the Born-Oppenheimer approximation or in the description of atoms and molecules in self-consistent field approximations. In most cases the use of numerical methods is necessary, where analytical solutions are not possible or difficult to find and the number of exactly solvable problems is very limited [1] . Over the past decade, several numerical methods have been developed for the solution of the Schrödinger equation, such as the Nikiforov-Uvarov (NU) method, Runge-Kutta methods, Matrix Diagonalization Method (MDM), Discrete Variable Method (DVM), Spectral Method [2] - [6] , and the asymptotic iteration method (A.I.M).
Ever since the inception of empirical Morse potential about 85 years ago, a vast number of potential functions have been reported for molecules, with varying degrees of flexibility and accuracy [7] . In this work we are interested to calculate the eigenvalues of hyperbolic single wave potential introduced by H. Bahlouli and A. D. Alhaidari [8] [9] some years ago. The new solvable hyperbolic single wave potential introduced given as
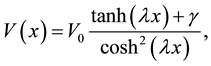 (1)
(1)
where 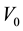 and
and 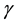 are real potential parameters and
are real potential parameters and  is a length scale that determines the range of the potential. The first term of this potential is completely new and cannot be predicted by any of the classical approaches based on diagonal representations. However, the second part is a special case of the hyperbolic Pöschl-Teller potential that has an exact conventional (diagonal representation) solution. Physically, the most interesting situation is when the parameter
is a length scale that determines the range of the potential. The first term of this potential is completely new and cannot be predicted by any of the classical approaches based on diagonal representations. However, the second part is a special case of the hyperbolic Pöschl-Teller potential that has an exact conventional (diagonal representation) solution. Physically, the most interesting situation is when the parameter 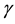 lies between
lies between  and
and 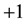 in which case the shape of this potential becomes a hyperbolic single wave about the origin [8] [9] . The potential has two local extrema at
in which case the shape of this potential becomes a hyperbolic single wave about the origin [8] [9] . The potential has two local extrema at
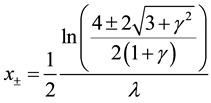 (2)
(2)
They have dealt with the case  which carries a richer structure for a given potential.
which carries a richer structure for a given potential.
In [8] they have dealt with case 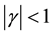 which carries a richer structure for a given potential. The configuration of this potential allows for both resonances and bound states, which is contrary to the case
which carries a richer structure for a given potential. The configuration of this potential allows for both resonances and bound states, which is contrary to the case 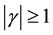
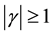
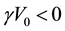
This paper is divided into the following sections. In Section 2, we describe the asymptotic iteration method which introduced to find the solutions for the second-order differential equation. In Section 3, change of variables has been done which allows as transforming Schrödinger equation to another form in order to apply the method to solve the equation with hyperbolic single wave potential. In Section 4, our numerical calculation results have been presented for the eigenvalues of the hyperbolic single wave potential.
2. Solution Methodology
Recently a technique called the asymptotic iteration method (AIM) has been introduced [10] to obtain eigenvalues of second-order homogeneous differential equations. In the case of the Schrödinger equation the AIM was found to reproduce the energy spectrum exactly for most exactly solvable potentials [11] - [13] , while for non- exactly solvable potentials it produces very good results [14] - [18] .
The first step in applying this method to solve Schrödinger-type equations is to transform these equations, with the aid of appropriate asymptotic forms, to second-order homogeneous linear differential equations of the general form
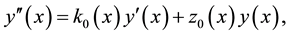
where the primes of 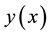
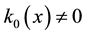
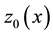
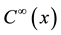
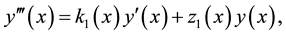
where
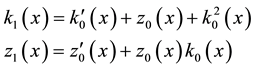
By differentiating Equation (4), we get
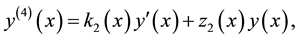
for which
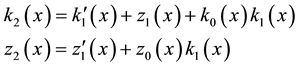
In general, the 
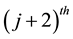
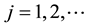
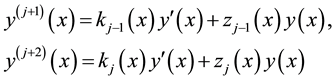
Respectively, where
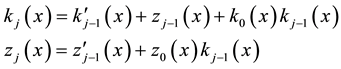
The ratio of the 
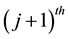
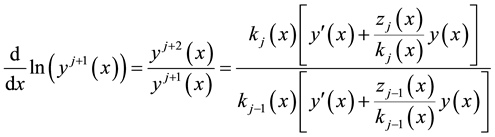
For sufficiently large j, we can introduce the “asymptotic” aspect of the method, that is, if
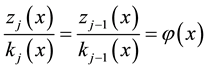
Thus, Equation (13) can be reduced to
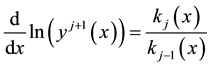
Which yields

where 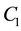
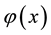
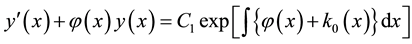
Which, in turn, yields the general solution to Equation (3)
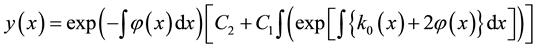
3. Formulation of the Problem
The time-independent Schrödinger equation, in the field of potential 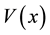

where 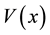
Substituting Equation (1) into Schrödinger equation (16) we obtain
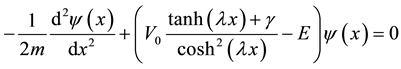
Before applying AIM to this problem, we have to transform the modified Schrödinger equation (17) to an amenable form for AIM. By using the change of variables, we can simplify Equation (17) by eliminating the hyperbolic functions 
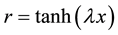
After making the convenient change of variable, a straightforward calculation shows that Equation (17) becomes
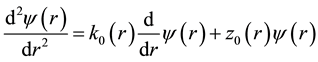
With 
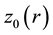
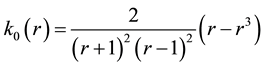
and
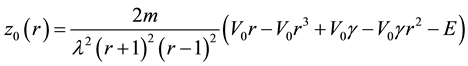
AIM can be applied to the final form of the Schrödinger equation (19).
In order to calculate the eigenvalues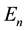

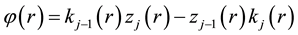
In each iteration, the expansion will depend on two variables E and r. The calculated eigenvalues 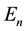

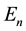
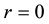
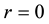
4. Results and Discussions
In this section, the paper shows the results of applying and using of AIM numerically, also the results of the calculations show that the AIM is powerful and the spectrum of energy for hyperbolic single wave potential can be obtained for all energy states. The resulting energy levels of the AIM are not limited by the magnitude of the parameters 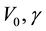
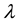
This paper aims to compute the energy spectrum which has not been computed in [8] [9] . To the best of our knowledge, this paper is the first study to compute the eigenenergies for the hyperbolic single wave potential. Before presenting the results, test where made to find out whether the AIM is suitable for finding the energy spectrum for hyperbolic single wave potential. Table 1, elucidate the rate of convergence of the AIM for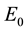
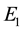
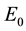
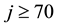
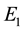
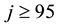
Comparing these results with the results obtained through a private communication with the authors of [8] [9] which are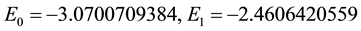
The conclusion to be drawn from this behavior which taken from Table 1, is that for the application of the method, the number of iterations depends on the degree of convergence required. In order to get accurate result for higher excited states, one needs to increase the number of iterations j for 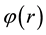
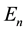
Table 2 a comparison between AIM results and numerical results obtained through a private communication with the authors of [8] [9] are made for the potential (1) with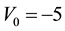
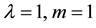
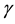
Table 1. The rate of convergence of the AIM for the eigenenergies of the lowest states E0, E1 with hyperbolic single wave potential in Equation (1) with V0 = 5, λ = 0.2, γ = −0.4, and m = 1, computed for a number of iterations j.
Table 2. A comparison of the energy eigenvalues En of the potential (1) with λ = 1, V0 = −5, m = 1 and for different parameter γ.
In conclusion, AIM was used to obtain the energy spectrum hyperbolic single wave potential. One can note that the method gives the eigenvalues if one can transform the Schrödinger equation into a form of
Acknowledgements
I would like to express my gratitude to Prof. H. Bahlouli, and Prof. A. D. Alhaidari for their valuable comments, encouragement, and discussion to complete this paper. Without their valuable efforts and guidance this paper wouldn’t have been accomplished.
Cite this paper
Abdallah J.Sous, (2015) The Asymptotic Iteration Method for the Eigenenergies of the a Novel Hyperbolic Single Wave Potential. Journal of Applied Mathematics and Physics,03,1406-1411. doi: 10.4236/jamp.2015.311168
References
- 1. Alhaidari, G.A.D. (2007) Representation Reduction and Solution Space Contraction in Quasi-Exactly Solvable Systems. Journal of Physics A: Mathematical and Theoretical, 40, 6305-6328.
http://dx.doi.org/10.1088/1751-8113/40/24/004 - 2. Asgarifar, S. and Goudarzi, H. (2013) Exact Solutions of the Manning-Rosen Potential Plus a Ring-Shaped Like Potential for the Dirac Equation: Spin and Pseudospin Symmetry. Physica Scripta, 87, 025703.
http://dx.doi.org/10.1088/0031-8949/87/02/025703 - 3. Liu, K., Shi, W. and Wu, X.Y. (2013) An Extended Discrete Gradient Formula for Oscillatory Hamiltonian Systems. Journal of Physics A: Mathematical and Theoretical, 46, 165203.
- 4. Moler, C.B. and Stewart, G.W. (1973) An Algorithm for Generalized Matrix Eigenvalue Problems. SIAM Journal on Numerical Analysis, 10, 241.
http://dx.doi.org/10.1137/0710024 - 5. Suslov, S.K. (2010) Dynamical Invariants for Variable Quadratic Hamiltonians. Physica Scripta, 81, 055006.
- 6. Pearman, C.M. (2014) An Excel-Based Implementation of the Spectral Method of Action Potential Alternans Analysis. Physiological Reports, 2, e12194.
http://dx.doi.org/10.14814/phy2.12194 - 7. Roy, A.K. (2014) Studies on the Bound-State Spectrum of Hyperbolic Potential. Few-Body Systems, 55, 143-150.
http://dx.doi.org/10.1007/s00601-013-0767-1 - 8. Bahlouli, H. and Alhaidari, A.D. (2010) Extending the Class of Solvable Potentials: III. The Hyperbolic Single Wave. Physica Scripta, 81, 025008.
http://dx.doi.org/10.1088/0031-8949/81/02/025008 - 9. Alhaidari, A.D. and Bahlouli, H. (2009) Two New Solvable Potentials. Journal of Physics A: Mathematical and Theoretical, 42, No. 26.
http://dx.doi.org/10.1088/1751-8113/42/26/262001 - 10. Ciftci, H., Hall, R.L. and Saad, N. (2003) Asymptotic Iteration Method for Eigenvalue Problems. Journal of Physics A: Mathematical and Theoretical, 36, 11807.
http://dx.doi.org/10.1088/0305-4470/36/47/008 - 11. Ciftci, H., Hall, R.L. and Saad, N. (2005) Construction of Exact Solutions to Eigenvalue Problems by the Asymptotic Iteration Method. Journal of Physics A: Mathematical and General, 38, 1147-1155.
http://dx.doi.org/10.1088/0305-4470/38/5/015 - 12. Saad, N., Hall, R.L. and Ciftci, H. (2006) Sextic Anharmonic Oscillators and Orthogonal Polynomials. Journal of Physics A: Mathematical and General, 39, 8477-8486.
http://dx.doi.org/10.1088/0305-4470/39/26/014 - 13. Ozer, O. and Roy, P. (2009) The Asymptotic Iteration Method Applied to Certain Quasinormal Modes and Non Hermitian Systems. Central European Journal of Physics, 7, 747-752.
- 14. Sous, A.J. (2006) Exact Solutions for a Hamiltonian Potential with Two-Parameters Using the Asymptotic Iteration Method. Chinese Journal of Physics, 44, 167-171.
http://psroc.phys.ntu.edu.tw/cjp/download.php?type=paper&vol=44&num=3&page=167 - 15. Soylu, A., Bayrak, O. and Boztosun, I. (2007) An Approximate Solution of Dirac-Hulthén Problem with Pseudospin and Spin Symmetry for Any. Journal of Mathematical Physics, 48, 082302.
http://dx.doi.org/10.1063/1.2768436 - 16. Barakat, T. (2005) The Asymptotic Iteration Method for the Eigenenergies of the Anharmonic Oscillator Potential . Physics Letters A, 344, 411-417.
http://dx.doi.org/10.1016/j.physleta.2005.06.081 - 17. Sous, A.J. (2006) Solution for the Eigenenergies of the Sextic Anharmonic Oscillator . Modern Physics Letters A, 21, 1675.
- 18. Sous, A.J. and EL-Kawni, M.I. (2009) General Eigenvalue Problems with Unbounded Potential from Below. International Journal of Modern Physics A, 24, 4169.
http://dx.doi.org/10.1142/s0217751x09044280


