Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59489,7 pages
10.4236/jamp.2015.39138
Comparison between Simple and Advanced Data Analysis to Pure Oxygen Absorption Spectrum at the 1270 nm Band
Muhammad A. Al-Jalali
Physics Department, Faculty of Science, Taif University, Taif, Kingdom of Saudi Arabia
Email: aljalaliphys@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
Simple and advanced data analysis was carried out on the pure oxygen absorption spectrum by Voigt deconvolution method between 1200 - 1300 nm, which represented the near-infrared spectrum. Pressures were 1, 5, 10, 15, 20, and 25 bars at 298 K. Experimental spectral lines showed two peaks at 1264 nm belong to O2 dimol and 1268 nm wavelength belong to O2 monomer, but advanced analysis of spectral lines gave many peaks around those two peaks. The total number of energy levels (peaks) decreases when pressure increases.
Keywords:
O2 Monomer, O2 Dimol, Voigt Deconvolution, Gaussian Width, Lorentzian Width, Voigt FWHM

1. Introduction
The famous paper, which was written to treat the comprehensive oxygen spectrum, belonged to Krupenie [1] , and a huge amount of data could be taken from The HITRAN molecular spectroscopic database [2] . And a group of Smith et al. published many excellent papers about oxygen spectrum, especially, at 1270 nm band, and another band [3] -[10] .
In the near-IR, experimental lines of pure oxygen absorption at 1270 nm band show, apparently, two kinds of absorptions: the first is a discrete line from individual O2 molecules (O2 monomer), and the second is a continuum band, which arises from collision complexes of O2, such as O2-O2 (O2 dimol (oxygen binary of O2-O2)). A continuous absorption band is characterized by O2 dimol, which is a consequence of collision-induced absorption (CIA) by two O2 in the electrically excited states [11] -[13] .
The lowest singlet electronic excitation energy from the O2 ground state is:
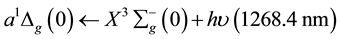 (1)
(1)
The ground state of O2-O2 is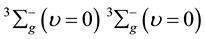 , and the first lowest electronic excitation energy from the O2 dimol ground state due to the following processes:
, and the first lowest electronic excitation energy from the O2 dimol ground state due to the following processes:
 (2)
(2)
Mechanisms of relation (1) are different from the relation (2), because the first comes from O2 discrete line where the second comes from O2-O2 band spectra.
Most excitations come from natural width according to Heisenberg’s uncertainty principle that is subject to Lorentzian or natural line. Collisional broadening contributes to the collision line shape by Lorentz distribution function, and the Doppler broadening depends on the Maxwell velocity distribution in a gas, where the Doppler line shape is Gaussian. In many sometimes, conditions require consideration of all effects as the convolution of Voigt profile.
The Gaussian temperature (Doppler)-broadened profile and a collision (Lorentzian)-broadened profile are given as follows:
 (3)
(3)
Whereas, a Voigt profile, mathematically, is the convolution of the Gaussian and the Lorentzian intensities:
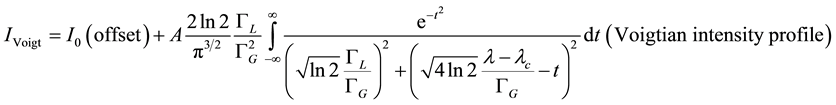 (4)
(4)
I = absorption intensity, I0 = offset absorption intensity, A = absolute area under the spectral line (integrated absorption intensity), 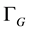 = Gaussian width,
= Gaussian width, 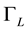 = Lorentzian width,
= Lorentzian width, 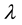 = wavelength,
= wavelength, 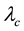 = central wavelength.
= central wavelength.
Humlíček [14] developed a Voigt profile, and gave the equation of the Voigt spectral line width (Voigt FWHM (full width at half-maximum height) as follows:
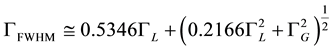 (5)
(5)
When Doppler (Gaussian) component is constant and small, Lorentzian distribution will prevail.
Voigt deconvolution method is the opposite of Voigt convolution method. It aims to analyze every spectral line to their components. The simple method denotes to analyzing one or two of visible peaks, whereas the advanced method is a full survey to all peaks and analyzes all appeared and disappeared peaks to their components.
The aim of this paper is to analyze the experimental results of pure oxygen spectrum at 1270 nm band by a simple and advanced Voigt deconvolution method.
2. Experimental
All spectra measurements of pure oxygen were carried out at the spectroscopy laboratory. Absorption spectrum in the NIR was recorded under the mode of baseline corrections by using Cary5000 UV-VIS-NIR spectrophotometer, VARIAN Company, equipped with long-pathlength absorption cell (LPAC). The LPAC contains multipass optics in the White cell configuration with a fixed path length of 9.6 m, and its constant volume equal 1.7 L. The temperature was constant at 298 K and pressures of gas were 1, 5, 10, 15, 20, 25 bar. Experimental measurements were chosen to measure the absorbance as a function of wavelength in the near infrared region extended between 1200 - 1300 nm.
3. Data Analysis
Origin pro Lab program was used for simple and advanced data analysis. The absolute area under the spectral line (A), central wavelength (Xc),Gaussian (WG), Lorentzian (WL) width and full width at half-maximum height (FWHM) in each spectral line were exactly defined through the deconvolution method of the Voigt profile function.
Simple and advanced analysis of six samples from twenty-five samples was subjected to pressures extended from 1 to 25 bars at 298 K, 323 K, 348 K, and 373 K. In this paper, pressures, which were chosen, are 1, 5, 10, 15, 20, 25 bar at only 298 K, where other pressures will be dealt with in other papers.
Figure 1 shows tough data analysis to total oxygen spectrum between 1200 - 1300 nm. Figures 1(a)-(f) inside Figure 1 show the peaks number for each line, where the number of peaks decreases with pressures increasing.
4. Results and Discussion
Because of the highly density of peaks number between 1200 - 1300 nm, only peaks(lines) between 1260 - 1270 nm were taken into account, where the interested lines (1268 nm, 1264 nm) exist between these lines. All results and values were taken based on the absorbance intensity 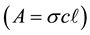 as a function of wavelength (nm).
as a function of wavelength (nm).
In addition, mathematical absolute area (integrated absorbance) under each main line was calculated to equal to sum of mathematical absolute areas for all separated lines by advanced data analysis, and absolute area (integrated absorbance) increases with increasing of pressure (see Figures 2-7).
All Figure 2(a), Figure 3(a), Figure 4(a), Figure 5(a), Figure 6(a), Figure 7(a) show how the main spectral line was separated from the Voigt deconvolution method to two spectral lines, the first belongs to O2 monomer at 1268 nm central wavelength, and the second to O2 binary absorbance at 1264 nm central wavelength. Whereas all Figure 2(b), Figure 3(b), Figure 4(b), Figure 5(b), Figure 6(b), Figure 7(b) show many spectral lines
Figure 1. Advanced analysis of spectral lines by Voigt deconvolution method (black line indicates the main spectral line, red line denotes to cumulative fit peak to main line, and the green line denotes to all analyzed spectral lines which came from analysis of main line (black line).
Figure 2. Simple and advanced data analysis at 1 bar and 298 K.
Figure 3. Simple and advanced data analysis at 5 bar and 298 K.
Figure 4. Simple and advanced data analysis at 10 bar and 298 K.
Figure 5. Simple and advanced data analysis at 15 bar and 298 K.
Figure 6. Simple and advanced data analysis at 20 bar and 298 K.
Figure 7. Simple and advanced data analysis at 25 bar and 298 K.
were made by advanced analysis between 1260 nm - 1270 nm, each line consist of two regions: the first belongs to discrete region, and the second belongs to continuous region.
Figures 2-4 show comparison between simple and advanced data analysis at 1, 5, 10 bar and constant temperature (298 k). The most important thing in advanced analysis, that there is a real discrete region with many wavelengths around the central wavelength (1268 nm) for O2 monomer with R and P branches, which belong to rotational spectrum. Whereas, the continuous region is wide and filled with spectral line around the central wavelength (1264 nm) for O2 dimol, where collision induced absorption (CIA) prevails in this region with a variety of energy levels (peaks).
Figure 5 and Figure 6 show, also, the comparison between simple and advanced data analysis at 15 and 20 bar and constant temperature (298 k). The main notices at these figures that the simple analysis gave factious values for central discrete line (1268 nm) and central continuous line (1264 nm), which mean that the discrete region was disappeared under pressures between 10 - 20 bar.
Figure 7 shows a strange result, where a very small initial discrete region began to appear, which needs to follow for pressures more than 25 bar.
Finally, it seems that at low pressures, the interactions and the competition between thermal effect (Doppler) and collisional effect (Lorentz) are very sensitive and active, and peaks number (energy levels) are very large. Whereas, at pressures higher than 10 bar the density of peaks will be more little. Figure 8 shows an exponential decay function between peaks number as a function of pressure (1 - 25 bar).
5. Conclusions
Voigt deconvolution method to separate two peaks from each other’s is a very successful method, and this method is able to give the values of Gaussian width (WG), Lorentzian width (WL), Voigt FWHM, and the integrated absorbance intensity for each peak.
Figure 2(a), Figure 3(a), Figure 4(a), Figure 5(a), Figure 6(a), Figure 7(a) reflect the simple analysis of each spectral line, which analyzes only two peaks belonging to central O2 discrete line (1268 nm) and central O2-O2 continuous line (1264 nm).
Whereas Figure 2(b), Figure 3(b), Figure 4(b), Figure 5(b), Figure 6(b), Figure 7(b) reflect the advanced analysis, which separates all energy levels (peaks), and each peak gives all information that is found in a two-
Figure 8. Peaks (energy levels) number as a function of pressure (1 - 25 bar).
peak method, which may belong to discrete or continuous bands.
The simple analysis may give factious values for some spectral lines under pressures between 10 - 20 bar, whereas advanced analysis gives almost real values for all spectral lines.
The pressure is very effective on absorption energy levels where their numbers exponentially decay with high pressures.
Acknowledgements
I am greatly indebted to Yahia M. Mahzia at the Physics Department, Faculty of Science, Damascus University for his comments and fruitful discussions about this work by private communication, where we have joint research projects in other papers.
Cite this paper
Muhammad A.Al-Jalali, (2015) Comparison between Simple and Advanced Data Analysis to Pure Oxygen Absorption Spectrum at the 1270 nm Band. Journal of Applied Mathematics and Physics,03,1114-1121. doi: 10.4236/jamp.2015.39138
References
- 1. Krupenie, P.H. (1972) The Spectrum of Molecular Oxygen. Journal of Physical and Chemical Reference Data, 1, No. 2, 423-534.
http://dx.doi.org/10.1063/1.3253101 - 2. Rothman, L.S., Gordon, I.E., Babikov, Y., Barbe, A., Benner, D.C., Bernath, P.F., Birk, M., et al. (2013) The HITRAN2012 Molecular Spectroscopic Database. Journal of Quantitative Spectroscopy & Radiative Transfer, 130, 4-50.
http://dx.doi.org/10.1016/j.jqsrt.2013.07.002 - 3. Smith, K.M. and Newnham, D.A. (2000) Near-Infrared Absorption Cross Sections and integrated Absorption Intensities of Molecular Oxygen (O2, O2-O2, and O2-N2). Journal of Geophysical Research, 105, 7383-7396.
- 4. Smith, K.M. and Newnham, D.A. (1999) Near-Infrared Absorption Spectroscopy of Oxygen and Nitrogen Gas Mixtures. Chemical Physics Letters, 308, 1-6.
http://dx.doi.org/10.1016/S0009-2614(99)00584-9 - 5. Smith, K.M., Newnham, A.D. and Williams, R.G. (2001) Collision-Induced Absorption of Solar Radiation in the Atmosphere by Molecular Oxygen at 1.27 μm: Field Observations and Model Calculations. Journal of Geophysical Research, 106, 7541-7542.
http://dx.doi.org/10.1029/2000JD900699 - 6. Newnham, D. and Ballard, J. (1998) Visible Absorption Cross Sections and Integrated Absorption Intensities of Molecular Oxygen (O2 and O4). Journal of Geophysical Research, 103, 28801-28815.
http://dx.doi.org/10.1029/98JD02799 - 7. Newman, S.M., Orr-Ewing, A.J., Newnham, D. and Ballard, J. (2000) Temperature and Pressure Dependence of Line Widths and Integrated Absorption Intensities for the O2 a1Δg-X3Σg-(0, 0) Transition. The Journal of Physical Chemistry A, 104, 9467-9480.
http://dx.doi.org/10.1021/jp001640r - 8. Maté, B., Lugez, C.L., Solodov, A.M., Fraser, G.T. and Lafferty, W.J. (2000) Investigation of the Collision-Induced Absorption by O2 near 6.4 μm in Pure O2 and O2/N2 Mixtures. Journal of Geophysical Research, 105, 222-225, 230.
http://dx.doi.org/10.1029/2000JD900295 - 9. Lemmon, E.W., Jacobsen, R.T., Penoncello, S.G. and Firend, D.G. (2000) Thermodynamic Properties of Air and Mixtures of Nitrogen, Argon, and Oxygen from 60 to 2000 K at Pressures to 2000 MPa. Journal of Physical and Chemical Reference Data, 29, 331-385.
http://dx.doi.org/10.1063/1.1285884 - 10. Sneep, M., Ityaksov, D., Aben, I., Linnartz, H. and Ubachs, W. (2006) Temperature-dependent cross sections of O2-O2 Collision-Induced Absorption Resonances at 477 and 577 nm. Journal of Quantitative Spectroscopy & Radiative Transfer, 98, 405-424.
www.elsevier.com/locate/jqsrt
http://dx.doi.org/10.1016/j.jqsrt.2005.06.004 - 11. Badger, R.M., Wright, A.C. and Whitlock, R.F. (1965) Absolute Intensities of the Discrete and Continuous Absorption Bands of Oxygen Gas at 1.26 and 1.065 Micron and the Radiative Lifetime of the 1Δ g State of Oxygen. The Journal of Chemical Physics, 43, 4345.
http://dx.doi.org/10.1063/1.1696694 - 12. Mate’, B., Lugez, C., Fraser, G.T. and Lafferty, W.J. (1999) Absolute Intensities for the O2 1.27 Micrometer Continuum Absorption. Journal of Geophysical Research, 104, 585-590.
http://dx.doi.org/10.1029/1999JD900824 - 13. Greenblatt, G.D., Orlando, J.J., Burkholder, J.B. and Ravishankara, A.R. (1990) Absorption Measurements of Oxygen between 330 and 1140 nm. Journal of Geophysical Research, 95, 18577-18582.
http://dx.doi.org/10.1029/JD095iD11p18577 - 14. Humlícek, J. (1982) Optimized Computation of the Voigt and Complex Probability Functions. Journal of Quantitative Spectroscopy and Radiative Transfer, 27, 437-444.
http://dx.doi.org/10.1016/0022-4073(82)90078-4









