Journal of Applied Mathematics and Physics
Vol.03 No.06(2015), Article ID:57408,6 pages
10.4236/jamp.2015.36080
Analytical Approach of the Nonlinear Surface Plasmon at a Left-Handed Material
Majdi S. Hamada1, Ali H. El-Astal1, Mahmoud A. Sbiah1, Mohammed M. Shabat2*
1Department of Physics, Al-Aqsa University, Gaza, Gaza Strip, Palestinian Authority
2Department of Physics, The Islamic University of Gaza, Gaza Strip, Palestinian Authority
Email: *shabat@iugaza.edu.ps
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2015; accepted 21 June 2015; published 25 June 2015
ABSTRACT
The surface wave dispersion relations of surface Plasmon at the interface of a left-handed material and a non-linear Kerr medium of arbitrary nonlinearity are derived based on a generalized first integral approach. The normalized power flow is also investigated for various values of frequency. The above study is conducted for both cases: self-focusing ( ) and de-focusing (
) and de-focusing (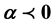 ) nonlinear Kerr coefficient.
) nonlinear Kerr coefficient.
Keywords:
Left-Handed Materials, Nonlinearity, Dispersion Relation, Power Flow

1. Introduction
Recently there are great interest and investigation of plasmonics. This is due to the increasing of transmission in layered thin films composed of metals and their experimental applications. Surface Plasmons are charges oscillations occurring at the interface between metal and dielectric layers. Plasmonics concerns with the surface Plasmons and the light interaction with metals.
The interaction of light and surface Plasmon has increased many applications and investigation studies such as developed spectroscopy, high resolution microscopy and sensing, development of light sources and cloaking left-handed materials.
Surface Plasmon excitation concerns with the free electrons oscillation of the interface between metal and dielectric layers leading to the resultant excitation which depends of the optical properties of the two layers and the interface geometry between the two layers. The surface Plasmon excitation is also investigated at simple geometry interface where the left-handed material and the dielectric layers have an interface which is infinite planar [1] [2] .
In our study, a Kerr-nonlinear type dielectric has been investigated where the dielectric function of the dielectric media depends on the electric field intensity. The surface Plasmons dispersion equation at a planar interface between a metal layer and a linear optical layer (where the wave number is k and the angular frequency is ω) can be expressed as the following:
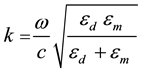 (1)
(1)
where c is the speed of light in vacuum and the 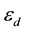 and
and  are dielectric functions of the dielectric and the metal, respectively, which can depend only on the frequency. Nonlinear dielectric-metal interface cases have also been investigated showing that the surface Plasmon can be excited by both TM and TE waves [3] - [5] . For such cases, the nonlinear surface Plasmon system is leading to the optical bistability, which has been observed recently in the transmission spectrum [6] and in the Goos-Handen shift [7] . It was also found that Equation (1) can be used with the dielectric function
are dielectric functions of the dielectric and the metal, respectively, which can depend only on the frequency. Nonlinear dielectric-metal interface cases have also been investigated showing that the surface Plasmon can be excited by both TM and TE waves [3] - [5] . For such cases, the nonlinear surface Plasmon system is leading to the optical bistability, which has been observed recently in the transmission spectrum [6] and in the Goos-Handen shift [7] . It was also found that Equation (1) can be used with the dielectric function 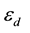 of the intensity-dependent medium (nonlinear medium) where
of the intensity-dependent medium (nonlinear medium) where 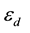 can be written as:
can be written as:
 (2)
(2)
where ε is the linear part and α is a nonlinear dielectric coefficients, which frequency-dependent.
In recent years, there has been an increasing growing interest in new artificial metamaterials. One of the most important reasons is due to the unusual characteristics and behaviors. Some of new interesting application of metamaterial is to use the left handed material or metamaterial in construction optical wave guide sensors [8] [9] .
Instead of a semi-infinite metallic region, we study here the surface Plasmon dispersion relation of a left- handed material (LHM). LHM is a medium with negative permittivity, permeability, and refractive index, which was initially discussed by Veselago [10] in the microwave frequency and could restore the evanescent wave- field components, being thus termed a perfect lens. Nowadays, the efforts have been made to design LHMs for optical frequencies using metallic nanowires [11] . Additionally, it was shown that photonic crystals demonstrate negative refraction under some conditions [12] , thus resembling the most famous feature of LHMs. Many other features of LHM were studied in published papers [13] - [15] . In this work, we also used the correct method (first integral approach) to derive the dispersion relation and present numerical analysis on the limitation of the inexact treatment by comparing its results with the correct theory.
2. Theory
ollowing the theory and approach of a TM-polarized wave which is considered to be propagated at the interface of a Kerr-type medium and a LHM, and by ignoring any loss in both media [16] . So we can easily find out the dispersive relation as follows; For simplicity, we take an isotropic Kerr medium as described in Equation (2), i.e.
 . For the case of anisotropic media, it is rather mathematically tedious [13] . In TM waves (Figure 1), we have only y component for H Field, and the electric field in both the nonlinear medium (
. For the case of anisotropic media, it is rather mathematically tedious [13] . In TM waves (Figure 1), we have only y component for H Field, and the electric field in both the nonlinear medium ( ) and the LHM (
) and the LHM (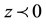 ) in general can be written as:
) in general can be written as:
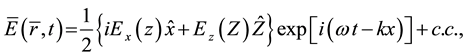 (3)
(3)
where c.c. is complex conjugate constant, and the relative phase of the two components 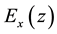 and
and 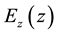 is out of phase
is out of phase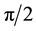 . The components of the amplitudes
. The components of the amplitudes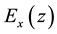 ,
, 


Figure 1. Geometry of the problem.
The solution of Maxwell Equations (4) in the LHM (

ponent electric field amplitude will have the form: 



The losses are neglected. Here 


where Dz is the z component of the electric induction vector D. Equation (6) hold in a linear medium with replaced εd by εeff .
The continuity of 


with


A standard treatment of the nonlinear region 1 invokes a “first integral” to get at an equation for 


An integration with respect to z gives

where C is an integration constant. The key step is to recognize the identity

The Equation (9) can be rewritten as

Applying the boundary conditions, 




Applying the boundary conditions at Equation (11)



where 


Furthermore, using Equation (7) together with the relation

where 

Now let us apply the above results to derive an explicit and exact dispersion relation for the surface Plasmon at a LHM-Kerr dielectric interface. Substituting Equation (14) into Equation (13), the result can finally be reduced to a quadratic equation in the wave number k which, leading to the following relation:

Putting the limits 










which are unacceptable since these will make k = 0 in Equation (15). Thus, we obtain the following implicit expression for 

Then, the surface plasmon frequency can be solved from Equation (16) to give the following relation:

This result is compared and contrasted with the one from the inexact approach [18] , namely,

Note that even in the weak field limit, Equation (17) implies that:

which contains an extra factor of 1/2 compared within Equation(18).
The power flow in the LHM linear medium is given by:

And the power flow in the nonlinear medium is written as:

3. Results and Discussions
It has been noticed that the dispersion curves are obviously changed by the effect of the nonlinearity for both self-focusing (

In Figure 3, Surface Plasmon frequency 






real solution of 
The normalized power 




4. Conclusion
It is noticed from our above treatment that the dispersion curves are strongly dependent on the intensity of the electric field. The most important conclusions are that for 
Figure 2. Dispersion curves for different electric field strength: Eo = 0 (curve 1) and 


Figure 3. The surface plasmon frequency versus the field intensity for different value of 

Figure 4. The normalized power P/Po for different values of frequency: f = 5.1 GHz (curve 1), f = 5.15 GHz (curve 2), and f = 5.19 GHz (curve 3) for
Figure 5. The normalized power P/Po for different values of frequency: f = 5.11 GHz (curve 1), f = 5.15 GHz (curve 2), and f = 5.17 GHz (curve 3) for
creases monotonically with 



versal and bistability cases have been clearly observed. The two interesting behaviors could lead to new design of future application in Optoelectronic-Microwave technology.
References
- Dionne, J.A., Verhagen, E., Polman, A. and Atwater, H.A. (2008) Are Negative Index Materials Achievable with Surface Plasmon Waveguides? A Case Study of Three Plasmonic Geometries. Optics Express, 16, 19001-19017. http://dx.doi.org/10.1364/OE.16.019001
- Tsakmakidis, K.L., Hermann, C., Klaedtke, A., Jamois, C. and Hess O. (2006) Surface Plasmon Polaritons in Generalized Slab Heterostructures with Negative Permittivity and Permeability. Physical Review B, 73, Article ID: 085104. http://dx.doi.org/10.1103/PhysRevB.73.085104
- Glass, N.E. and Rogovin, D. (1989) Surface-Polariton and Guided-Wave Excitation in Thin-Film Kerr Media. Physical Review B, 40, 1511. http://dx.doi.org/10.1103/PhysRevB.40.1511
- Smolyaminoy, I.L., et al. (2002) Single-Photon Tunneling via Localized Surface Plasmons. Physical Review Letters, 88, Article ID: 187402. http://dx.doi.org/10.1103/PhysRevLett.88.187402
- Baher, S. and Cottam, M.G. (2004) Theory of Nonlinear s-Polarized Phonon-Polaritons in Multilayered Structures. Journal of Science, 15, 171-177.
- Wurtz, G.A., Potrald, R. and Zayats, A.V. (2006) Optical Bistability in Nonlinear Surface-Plasmon Polaritonic Crystals. Physical Review Letters, 97, Article ID: 057402. http://dx.doi.org/10.1103/PhysRevLett.97.057402
- Zhou, H., Chen, X., Hou, P. and Li, C.F. (2008) Giant Bistable Lateral Shift Owing to Surface Plasmon Excitation in Kretschmann Configuration with a Kerr Nonlinear Dielectric. Optical Letters, 33, 1249-1251. http://dx.doi.org/10.1364/OL.33.001249
- Taya, S.A., Shabat, M.M. and Khalil, H.M. (2009) Enhancement of Sensitivity in Optical Waveguide Sensors Using Left-Handed Materials. Optik, 120, 504-508. http://dx.doi.org/10.1016/j.ijleo.2007.12.001
- Taya, S.A., Shabat, M.M. and Khalil, H.M. (2008) Analysis of TM Nonlinear Asymmetrical Waveguide Optical Sensors. Sensors and Actuators A: Physical, 147, 137-141. http://dx.doi.org/10.1016/j.sna.2008.05.002
- Veselago, V.G. (1968) The Electrodynamics of Substances with Simultaneously Negative Values of ε and μ. Soviet Physics Uspekhi, 10, 509-514. http://dx.doi.org/10.1070/PU1968v010n04ABEH003699
- Podolskiy, V.A., Sarychev, A.K. and Shalaev, V.M. (2002) Plasmon Modes in Metal Nanowires and Left-Handed Materials. Journal of Nonlinear Optical Physics & Materials, 11, 65-74. http://dx.doi.org/10.1142/S0218863502000833
- Notomi, M. (2000) Theory of Light Propagation in Strongly Modulated Photonic Crystals: Refractionlike Behavior in the Vicinity of the Photonic Band Gap. Physical Review B, 62, 10696-10705. http://dx.doi.org/10.1103/PhysRevB.62.10696
- Hamada, M.S., El-Astal, A.H. and Shabat, M.M. (2007) Nonlinear TE Surface Waves in a Photosensitive Semiconductor Film Bounded by a Superconductor Cover. International Journal of Modern Physics B, 21, 1817-1825. http://dx.doi.org/10.1142/S0217979207037065
- Hamada, M.S., El-Astal, A.H. and Shabat, M.M. (2007) Characteristic of Surface Waves in Nonlinear Left-Handed- Photosensitive-Semiconductor Waveguide Structure. International Journal of Modern Physics B, 21, 5319-5329. http://dx.doi.org/10.1142/S0217979207038459
- Hamada, M.S., Ass’ad, A.I., Ashour, H.S. and Shabat, M.M. (2006) Nonlinear Magnetostatic Surface Waves in a Ferrite-Left-Handed Waveguide Structure. Journal of Microwaves and Optoelectronics, 5, 45-54.
- Mihalache, D., Nazmitdinov, R.G. and Fedyanin, V.K. (1989) Nonlinear Optical Waves in Layered Structure. Soviet Journal of Nuclear Physics, 20, 86-107.
- Economou, E.N. (1969) Surface Plasmons in Thin Films. Physical Review, 182, 539-554. http://dx.doi.org/10.1103/PhysRev.182.539
- Waysin, G.M., Simon, H.J. and Deck, R.T. (1981) Optical Bistability with Surface Plasmons. Optics Letters, 6, 30-32. http://dx.doi.org/10.1364/OL.6.000030
NOTES
*Corresponding author.







