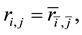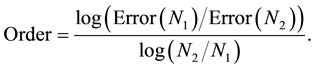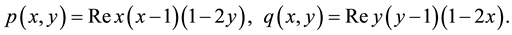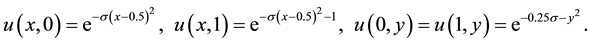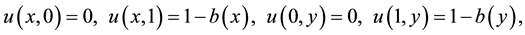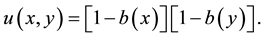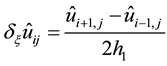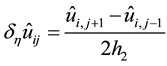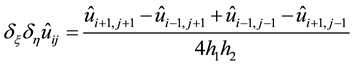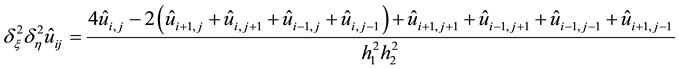Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56416,14 pages
10.4236/jamp.2015.35063
High Order Compact Difference Scheme and Multigrid Method for 2D Elliptic Problems with Variable Coefficients and Interior/Boundary Layers on Nonuniform Grids
Bin Lan1, Yongbin Ge1*, Yan Wang1, Yong Zhan2
1Institute of Applied Mathematics and Mechanics, Ningxia University, Yinchuan, China
2Department of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai, China
Email: *gyb@nxu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 April 2015; accepted 16 May 2015; published 19 May 2015
ABSTRACT
In this paper, a high order compact difference scheme and a multigrid method are proposed for solving two-dimensional (2D) elliptic problems with variable coefficients and interior/boundary layers on nonuniform grids. Firstly, the original equation is transformed from the physical domain (with a nonuniform mesh) to the computational domain (with a uniform mesh) by using a coordinate transformation. Then, a fourth order compact difference scheme is proposed to solve the transformed elliptic equation on uniform girds. After that, a multigrid method is employed to solve the linear algebraic system arising from the difference equation. At last, the numerical experiments on some elliptic problems with interior/boundary layers are conducted to show high accuracy and high efficiency of the present method.
Keywords:
Elliptic Equation, Coordinate Transformation, High Order Compact Difference Scheme, Multigrid Method, Interior/Boundary Layer

1. Introduction
Elliptic equations are widely used in the fields of solid mechanics, material science, and image processing and so on. So it is both theoretically and practically important to investigate numerical methods for such equations. Finite difference method is a general and effective method to solve elliptic equations. In the past three decades, a large number of high order compact (HOC) difference schemes [1] -[14] have been developed to overcome the deficiencies (lower accuracy or numerical oscillation, etc.) of the conventional difference schemes. These HOC schemes own high accuracy with small mesh stencil and very effective for solving the problems with smooth solutions. And they can suppress numerical oscillations that may occur if standard second order central difference scheme is used to solve the convection-dominated problem or high Reynolds number problems [12] . But we notice that many HOC schemes among them are constructed directly on the uniform grids because it is easy to be implemented in practice. However, for the computation of many problems whose physical quantities unevenly distributed in spaces or with areas of steep solution gradients, the advantages of the HOC scheme may be lost if there were no enough grid points inside the large gradient areas. Very fine discretization could be used in the whole domain to yield an approximate solution of acceptable accuracy with uniform grids. But such a fine discretization results in a very large linear system that demands a large computational cost. In other words, it would lead huge waste of computational amount if uniform grids are used in the whole physical domain. To avoid too many grid points in the computational domain and to reduce the total computational cost, we can place clustered mesh grids in the area of large gradient while relatively few grids in the smooth region. So, developing efficient difference schemes on nonuniform grids has a very important application value and actual significance.
Coordinate transformation method [11] -[15] is a commonly-used method to achieve computation on physical nonuniform grids. This method needs to transform the nonuniform grids in the physical domain to the uniform grids in the computational domain by using reversible coordinate transformation functions. After computation, it returns the computed results back to the physical domain by the inverse transformation. The method has its advantages. Firstly, it can be used to construct HOC schemes more easily on uniform grids than on nonuniform grids by discretizing the derivative terms directly; secondly, such transformations are also used to reflect many interior/boundary layer phenomena without refining the mesh near to the interior/boundary layers in the computational domain. A few researchers have used this method to deal with convection diffusion equations or Navier- Stokes equations. For instance, Choo and Schultz [11] used the transformation method and developed a fourth order compact difference scheme to solve the steady Navier-Stokes equations. The results show that the method is accurate and stable. Spotz [12] developed a class of HOC finite difference schemes for steady convection diffusion equation on uniform grids. And then he extended them to nonuniform grids by using the coordinate transformation method. Ge and Zhang [13] also solved the 2D convection diffusion equations with boundary layers using the coordinate transformation method and a fourth order scheme was applied on the uniform computational grids. The authors extended the coordinate transformation method to the three-dimensional (3D) case [14] to resolve 3D boundary layer problems. Liu C. and Liu Z. [15] employed the coordinate transformation and combined it with a fourth order finite difference scheme and multigrid method to simulate the whole process of flow transition in 3D boundary layers. If we fix our attention on elliptic equations, we notice that the coefficients of the first or second order derivatives in the original model equations considered in the literature are constant [11] -[14] . Although after coordinate transformation, the coefficients turn to be variable, the high order difference schemes, which are developed based on it, could not be used to compute the solutions of original model equations in which the coefficients of the first or second order derivatives are variable. So, the potential advantages of applying coordinate transformation method and HOC schemes to solve variable coefficients elliptic problems have not been fully investigated.
In this paper, we consider the 2D elliptic equation with variable coefficients as follows:
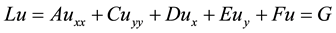 (1)
(1)
where  is unknown function and the coefficients A, C, D, E, F and the right hand term G are the functions of
is unknown function and the coefficients A, C, D, E, F and the right hand term G are the functions of  and are assumed to be continuously differentiable. We are aiming at developing an HOC scheme which is based on coordinate transformation and multigrid method to solve Equation (1) on nonuniform grids. The remainder of this paper is arranged as follows. Section 2 gives the method of coordinate transformation, which transforms nonuniform grids in physical domain onto uniform grids in computational domain. In Section 3, an HOC scheme on uniform grids is constructed to solve the transformed equation in the computational domain. After that, a multigrid method based on the HOC scheme is introduced in Section 4. In Section 5, numerical experiments are carried out to show the accuracy and efficiency of the present method. Especially, some problems with interior or boundary layers are considered in this section. Finally, some concluding remarks are given in Section 6.
and are assumed to be continuously differentiable. We are aiming at developing an HOC scheme which is based on coordinate transformation and multigrid method to solve Equation (1) on nonuniform grids. The remainder of this paper is arranged as follows. Section 2 gives the method of coordinate transformation, which transforms nonuniform grids in physical domain onto uniform grids in computational domain. In Section 3, an HOC scheme on uniform grids is constructed to solve the transformed equation in the computational domain. After that, a multigrid method based on the HOC scheme is introduced in Section 4. In Section 5, numerical experiments are carried out to show the accuracy and efficiency of the present method. Especially, some problems with interior or boundary layers are considered in this section. Finally, some concluding remarks are given in Section 6.
2. Coordinate Transformation
We consider a rectangular physical domain 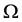 and
and  is its boundary. We transform the independent variables x and y in the physical domain into new independent variables
is its boundary. We transform the independent variables x and y in the physical domain into new independent variables 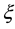 and
and 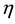 in the computational domain. The transformation functions are written as:
in the computational domain. The transformation functions are written as:
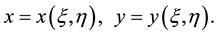 (2)
(2)
Then, Equation (1) is transformed into the form as:
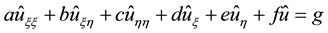 (3)
(3)
where the coefficients a, b, c, d, e, f and the right hand term g are the functions of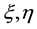 , and
, and
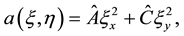 (4)
(4)
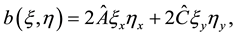 (5)
(5)
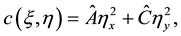 (6)
(6)
 (7)
(7)
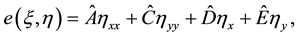 (8)
(8)
 (9)
(9)
where
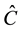




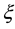



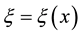




Then, for Equation (10), a fourth order compact difference scheme can be derived. We will give the derivation process of the fourth order compact scheme in the next section.
3. HOC Difference Scheme
Firstly, we divide the computational domain 
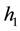
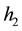
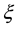

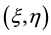
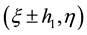







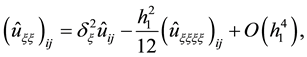


Then the following difference equation is got if we substitute Equations (11)-(15) into Equation (10):

Equation (16) is actually the second order central difference scheme and 
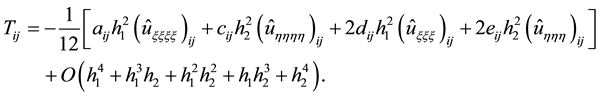
In order to get an HOC scheme, the third order and fourth order derivatives in 

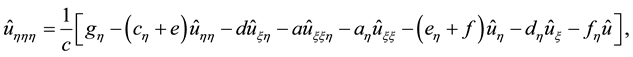


Using the central differences, the difference approximation of
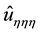







Finally, substituting Equations (22)-(25) into Equation (17), combining it with Equation (16) and neglecting high order truncation error term, we have:

where





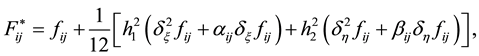

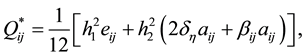



So Equations (26) with (27)-(37) is the HOC difference scheme based on the coordinate transformation for solving Equation (1) on nonuniform grids. The present HOC scheme can be written in the form of nine-point scheme and the corresponding coefficients of them can be written as follows:
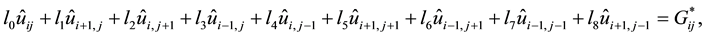
where






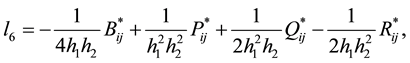


From the process of derivation, it is easy to know that the truncation error of this scheme is 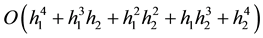
4. Multigrid Method
In order to solve the linear algebraic systems which are arising from various difference schemes, generally, some iterative methods are used. But the convergence speed of traditional iterative methods is very slow, so appears multigrid method [16] -[18] . It has been proved that multigrid method is an optimal numerical method at least for solving the linear elliptic problems. Its main characteristics is to use the traditional iterative methods to solve the residual equations on different coarse grid levels by gradually transferring the errors to coarser grids until the error is convergent, then to return the corrected results to the finer grid levels by using the interpolation.
Multigrid method is achieved by some circulation algorithms such as V cycle, W cycle or Full Multigrid V cycle (FMV) etc. The whole process has three elements: relaxation operator, projection operator and interpolation operator. The function of relaxation operator (or iteration) is to dump the high frequency components of the errors on the current grid. The function of projection and interpolation operators is to transfer error residuals from finer grids to coarser grids and to return the corrected errors from the coarser grids to the finer grids. The multigrid 


Multigrid method has been used to solve various linear elliptic equations such as Poisson equation [19] -[21] , convection-diffusion equations [22] -[25] and so on. Gupta et al. [19] [22] [24] and Zhang [20] [23] used it to solve the 2D and 3D Poisson equations and the convection diffusion equations discretized by the fourth order compact scheme on uniform grids. Ge and Cao [25] and Ge et al. [21] developed multigrid method on nonuniform grids to solve 2D convection diffusion equation and 3D Poisson equation with boundary layer problems based on the transformation-free HOC difference schemes. In terms of the method of coordinate transformation, Ge and Zhang [13] [14] used it to map the nonuniform grid to a uniform grid, and then employed a fourth order compact difference scheme to the transformed uniform grid and a multigrid method to solve the 2D and 3D convection diffusion equation with boundary layers.
In this paper, we adopt the multigrid V cycle method to solve the linear algebraic system arising from the difference schemes. In order to match the HOC scheme, we choose the full weighting projection operator on uniform grids [18]
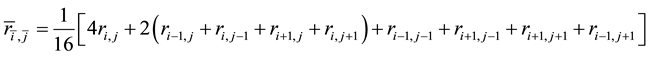
where 



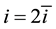
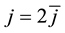
Then, for relaxation operator, we use the alternating direction line Gauss-Seidel relaxations to remove the residuals on each coarse grid.
5. Numerical Experiments
In order to demonstrate the high accuracy and high efficiency of the present method, we use it to solve the following three elliptic problems with Dirichlet boundary conditions. All of the problems have the exact solutions. All computation is started with zero initial guesses and is terminated when the residuals in 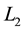
where 
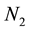

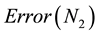
5.1. Problem 1
We consider the following 2D convection diffusion problem [26] :
where
The boundary conditions are:
The exact solution is:
This problem has a steep solution gradient near
where 

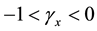





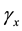
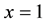

For this problem, we set Re = 1000 and choose 

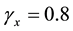

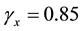





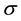

In order to illustrate the computational accuracy in the whole domain, with the grid number 64 × 64, we give the figures about the contours of the exact solution (Figure 1(b)), the computed results on uniform grids (Figure 1(c)) and on nonuniform grids (Figure 1(d)) for 
5.2. Problem 2
Next, we consider an elliptic problem as follows:
where
The boundary conditions are:
Table 1. Maximum absolute errors and the convergence rates for Problem 1, Re = 1000.
Figure 1. (a) Nonuniform grids (


in which
The exact solution is:
For this problem, there are two boundary layers near 

We choose Re = 10, 100 and 1000. From Table 2 we find that when Re = 10, the computation can approximately achieve fourth order convergence on both uniform and nonuniform grids

Table 2. Maximum absolute errors and the convergence rates for Problem 2.

Figure 2, with grid number 64 × 64, gives the contours of exact solution (Figure 2(b)), the computed results on uniform grids (Figure 2(c)) and on nonuniform grids (Figure 2(d)) for Re = 1000. We find that the present HOC scheme produces amazingly satisfying solution on nonuniform grids, while it appears a big computed error near the boundary layers on the uniform grids.
5.3. Problem 3
We consider the following elliptic equation:
The boundary conditions are:
The exact solution is:
There is a boundary layer near
For this problem, the multigrid V(2,2) cycles are used. Table 3 gives the computed results, where 


Figure 2. (a) Nonuniform grids (
Re = 10,000, it just gets the second order accuracy on the uniform grids, the computed errors are dramatically distorted with the increase of Re, and this gives very poor solution. Especially for Re = 10,000, the solution is very bad and unacceptable. Compared with computed results on the uniform grids, it shows that the fourth order accuracy is achieved for all the Re numbers on the nonuniform grids and the computed results are very accurate. So, it demonstrates that the present transformed HOC scheme is effective for solving the boundary layer problems with nonuniform grids in the physical domain. Table 3 also gives the numbers of multigrid V(2,2) iterations and the CPU time in seconds for this problem. We can see that the multigrid algorithm is very effective and the numbers of multigrid V(2,2) cycles are no more than 10 times to get convergence for all cases.
Figure 3 gives the comparison of the exact and the computed solutions with the grid number 64 × 64 while Re = 10,000 and the transformation parameter is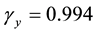
6. Concluding Remarks
The aim of this paper is to build an efficient and high accuracy numerical method for solving 2D elliptic equations with variable coefficients and interior/boundary layers on nonuniform grids. Coordinate transformation
Table 3. Maximum absolute errors and the convergence rates for Problem 3.
Figure 3. (a) Nonuniform grids (
method is employed to transfer nonuniform grids in the physical domain, which concentrates clustered grid points inside the interior/boundary layers, to uniform grids in the computational domain. A high order compact difference scheme is derived for the transformed equation to achieve the purpose of simplified calculation on uniform grids. It needs to be pointed out that when the transformation parameter is zero, the present HOC scheme reduces to the HOC difference scheme on uniform grids in the physical domain. So, it fits computation on both uniform and nonuniform grids. In order to accelerate the convergence of the traditional iterative methods and to reduce computational cost, a multigrid method is employed to solve the linear algebraic system which is arising from the difference scheme. Some numerical experiments with interior or boundary layer problems are conducted to demonstrate the performances of the present method. It indicates that a nonuniform grid is necessary for solving 2D elliptic problems with interior or boundary layers. By coordinate transformation, a certain number of grid points are clustered in the interior or boundary layers to guarantee that the HOC scheme for transformed equation obtains very accurate numerical solution with not so fine grids. Otherwise, the HOC scheme produces very poor approximation solution on uniform grids.
Acknowledgements
The present work was supported by the National Science Foundation of China under Grant 11361045 and 11161036, Fok Ying-Tong Education Foundation of China under Grant 121105.
References
- Lynch, R.E. and Rice, J.R. (1978) High Accuracy Finite Difference Approximation to Solutions of Elliptic Partial Differential Equations. Proceedings of the National Academy of Sciences of the United States of America, 75, 2541-2544. http://dx.doi.org/10.1073/pnas.75.6.2541
- Boisvert, R.F. (1981) Families of High Order Accurate Discretizations of Some Elliptic Problems. SIAM Journal on Scientific and Statistical Computing, 2, 268-284. http://dx.doi.org/10.1137/0902022
- Gupta, M.M., Manohar, R.P. and Stephenson, J.W. (1984) A Single Cell High Order Scheme for the Convection- Diffusion Equation with Variable Coefficients. International Journal for Numerical Methods in Fluids, 4, 641-651. http://dx.doi.org/10.1002/fld.1650040704
- Gupta, M.M., Manohar, R.P. and Stephenson, J.W. (1985) High-Order Difference Scheme for Two Dimensional Elliptic Equations. Numerical Methods for Partial Differential Equations, 1, 71-80. http://dx.doi.org/10.1002/num.1690010108
- Ananthakrishnaiah, U., Manohar, R. and Stephenson, J.W. (1987) High-Order Methods for Elliptic Equations with Variable Coefficients. Numerical Methods for Partial Differential Equations, 3, 219-227. http://dx.doi.org/10.1002/num.1690030306
- Ananthakrishnaiah, U., Manohar, R. and Stephenson, J.W. (1987) Fourth-Order Finite Difference Methods for Three- Dimensional General Linear Elliptic Problems with Variable Coefficients. Numerical Methods for Partial Differential Equations, 3, 229-240. http://dx.doi.org/10.1002/num.1690030307
- Ge, L.X. and Zhang, J. (2002) Symbolic Computation of High Order Compact Difference Schemes for Three Dimensional Linear Elliptic Partial Differential Equations with Variable Coefficients. Journal of Computational and Applied Mathematics, 143, 9-27. http://dx.doi.org/10.1016/S0377-0427(01)00504-0
- Choo, J.Y. (1994) Stable High Order Methods for Elliptic Equations with Large First Order Terms. Computers and Mathematics with Applications, 27, 65-80. http://dx.doi.org/10.1016/0898-1221(94)90006-X
- Karaa, S. (2007) High-Order Difference Scheme for 2D Elliptic and Parabolic Problems with Mixed Derivatives. Numerical Methods for Partial Differential Equations, 23, 366-378. http://dx.doi.org/10.1002/num.20181
- Briane, M. and Diaz, J.C. (2008) Uniform Convergence of Sequences of Solutions of Two-Dimensional Linear Elliptic Equations with Unbounded Coefficients. Journal of Differetial Equations, 245, 2038-2054. http://dx.doi.org/10.1016/j.jde.2008.07.027
- Choo, J.Y. and Schultz, D.H. (1994) A High Order Difference Method of Steady State Navier-Stokes Equation. Computers & Mathematics with Applications, 27, 105-119. http://dx.doi.org/10.1016/0898-1221(94)90101-5
- Spotz, W.F. (1995) High-Order Finite Difference Schemes for Computational Mechanics. Ph.D. Thesis, University of Texas at Austin.
- Ge, L.X. and Zhang, J. (2001) High Accuracy Iterative Solution of Convection Diffusion Equation with Boundary Layers on Nonuniform Grids. Journal of Computational Physics, 171, 560-578. http://dx.doi.org/10.1006/jcph.2001.6794
- Zhang, J., Ge, L.X. and Gupta, M.M. (2001) Fourth Order Compact Difference Scheme for 3D Convection Diffusion Equation with Boundary Layers on Nonuniform Grids. Neural, Parallel and Scientific Computations, 8, 373-392.
- Liu, C. and Liu, Z. (1995) Multigrid Mapping and Box Relaxation for Simulation of the Whole Process of Flow Transition in 3D Boundary Layers. Journal of Computational Physics, 119, 325-341. http://dx.doi.org/10.1006/jcph.1995.1138
- Brandt, A. (1977) Multi-Level Adaptive Solution to Boundary Value Problems. Mathematics of Computation, 31, 333- 390. http://dx.doi.org/10.1090/S0025-5718-1977-0431719-X
- Hackbusch, W. and Trottenberg, U. (1982) Multigrid Methods. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/BFb0069927
- Wesseling, P. (1992) An Introduction to Multigrid Methods. Wiley, Chichester.
- Gupta, M.M., Kouatchou, J. and Zhang, J. (1997) Comparison of Second- and Fourth-Order Discretizations for Multigrid Poisson Solvers. Journal of Computational Physics, 132, 226-232. http://dx.doi.org/10.1006/jcph.1996.5466
- Zhang, J. (1998) Fast and High Accuracy Multigrid Solution of the Three Dimensional Poisson Equation. Journal of Computational Physics, 143, 449-461. http://dx.doi.org/10.1006/jcph.1998.5982
- Ge, Y., Cao, F. and Zhang, J. (2013) A Transformation-Free HOC Scheme and Multigrid Method for Solving the 3D Poisson Equation on Nonuniform Grids. Journal of Computational Physics, 234, 199-216. http://dx.doi.org/10.1016/j.jcp.2012.09.034
- Gupta, M.M., Kouatchou, J. and Zhang, J. (1997) A Compact Multigrid Solver for Convection-Diffusion Equations. Journal of Computational Physics, 132, 123-129. http://dx.doi.org/10.1006/jcph.1996.5627
- Zhang, J. (1997) Accelerated Multigrid High Accuracy Solution of the Convection-Diffusion Equation with High Reynolds Number. Numerical Methods for Partial Differential Equations, 13, 77-92. http://dx.doi.org/10.1002/(SICI)1098-2426(199701)13:1<77::AID-NUM6>3.0.CO;2-J
- Gupta, M.M. and Zhang, J. (2000) High Accuracy Multigrid Solution of the 3D Convection-Diffusion Equation. Applied Mathematics and Computation, 113, 249-274. http://dx.doi.org/10.1016/S0096-3003(99)00085-5
- Ge, Y. and Cao, F. (2011) Multigrid Method Based on the Transformation-Free HOC Scheme on Nonuniform Grids for 2D Convection Diffusion Problems. Journal of Computational Physics, 230, 4051-4070. http://dx.doi.org/10.1016/j.jcp.2011.02.027
- Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Rordan, E. and Shishkin, G.I. (2000) Robust Computational Techniques for Boundary Layers. Chapman & Hall/CRC, Boca Raton.
Appendix
NOTES
*Corresponding author.