Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:58401,9 pages
10.4236/jamp.2015.37111
Reliability Analysis of a Redundant Cascade System by Using Markovian Approach
Nalabolu Swathi, Tallapureddy Sumathi Uma Maheswari
Department of Mathematics, Kakatiya University, Warangal, India
Email: swathinalabolu11@gmail.com, sumathiuma21@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 November 2014; accepted 26 July 2015; published 29 July 2015
ABSTRACT
In the present work, it is assumed that the n-components are arranged in the hierarchial order. The n-cascade system surviving with loss of m components by k number of attacks is studied; the general equation for the reliability is obtained for the above said system; and the system reliability is computed numerically for 6-cascade system for 2-number of attacks.
Keywords:
Cascade System, Redundancy, Reliability, Markov Process, k Attacks

1. Introduction
Reliability of a system is the probability that a system will adequately perform its intended purpose for a given period of time under stated environmental conditions [1] . In some cases system failures occur due to certain type of stresses acting on them. Thus system composed of random strengths will have its strength as random variable and the stress applied on it will also be a random variable. A system fails whenever an applied stress exceeds strength of the system. Probability and reliability were explained by Shooman [2] . The applications of time dependent stress strength models are explained by Schatz R. et al. [3] . Reliability of a n-cascade system with stress attenuation was proposed by Pandit & Sriwastav [4] . Estimation of reliability was explained by William [5] . Raghavachar et al. [6] [7] studied the reliability of a cascade system with normal stress & strength distri- bution and survival function under stress attenuation in cascade reliability. Detailed explanation of mixture distributions is given in [8] . T. S. Uma Maheswari [9] explained reliability of cascade system with normal stress & exponential strength. T. S. Uma Maheswari [10] studied reliability comparison of an n-cascade system with the addition of an n-strength system. T. S. Uma Maheswari [11] explained relaibility of single stress under n- strengths of life distribution. Rekha et al. [12] studied cascade system reliability with rayleigh distribution. In reliability theory, there are lots of real life situations where the concept of mixture distributions can be applied. For example, in life testing experiments, the systems will be failed due to different causes and the times to failure due to different reasons are likely to follow different distributions. Knowledge of these distributions is essential to eliminate cause of failures and thereby to improve the reliability. Maya, T. Nair [13] described the estimation of reliability based on finite mixture of pare to and beta distributions.
Stochastic process is a mathematical model that evolves over time in a probabilistic manner. A special kind of stochastic process is called Markov process, where the outcome of an experiment depends only on the outcome of the previous experiment, i.e., the next state of the system depends only on the present state, not on preceding states. Cascade redundancy is the provision of alternative means or parallel paths in a system for accomplishing a given task such that all means must fail before causing a system failure. The reliability model is being studied here. The probabilities of component failure depend on the relative positions of the particular components along the hierarchy.
It is assumed that the n-components are arranged in the hierarchical order as 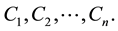 If
If  is the active component during an attack, let
is the active component during an attack, let 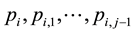 and
and 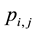 are the probabilities that
are the probabilities that 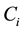 survives,
survives,  fails, but
fails, but 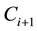 survives etc., and
survives etc., and 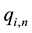 be the probability that the components
be the probability that the components  fail in the same attack. Thus, we have,
fail in the same attack. Thus, we have,  for
for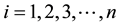 .
.
In the present, probability distribution of the number of attacks required for failure of a n-component hierarchical cascade system, as defined above, is investigated and the probability of the system surviving k attacks, sustained a loss of the first m components, is studied.
2. Notation and Explanations
 : Probability that a n-component system fails in the kth attack.
: Probability that a n-component system fails in the kth attack.
 : The corresponding probability distribution function
: The corresponding probability distribution function 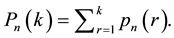
 : The corresponding probability generating function.
: The corresponding probability generating function.
 : The reliability of the n-component system surviving “k” attacks with a loss of “m” components.
: The reliability of the n-component system surviving “k” attacks with a loss of “m” components.




























consists of zeros except for unity at the 












Obviously,
Let a system consist of three components

3. Reliability Evaluation
Reliability of a System for k Attacks
Here consider the probability that the system survives “k” attacks with a loss of the first “m” components. Let 
The Two Component System:
For m = 0, we get
For m = 1, we have the corresponding event
The corresponding probability
here 
It is obvious that when m = 2
The Three Component System:
When m = 0, we get
When m = 1, we have the corresponding event
Hence
here 
When m = 2, the corresponding event
Hence
It is obvious that
The Four Component System:
When m = 0, we get
Similarly, for m = 1
For m = 2
For m = 3
For m = 4
The Five Component System:
For m = 0, we get
For m = 1, the corresponding probability
For m = 2,
For m = 3,
For m = 4,
For m = 5,
The Six Component System:
For m = 0, we get
For m = 1, the corresponding probability
For m = 2,
For m = 3,
For m = 4,
For m = 5,
For m = 6,
The general equation for probability of n-component system fails in the kth attack
The general equation for reliability of n-component system for kth attack
4. Example
Let us consider a transition probability matrix of order 7 for 6-component system
The first element in the ith column matrix represents the probability of failure of the system at the end of ith attack i.e.,
Let us find the reliability of above system in 2 number of attacks
5. Conclusion
The present work deals with the cascade reliability model represented as Markovian model. Reliability of stress strength model is derived with Markovian Approach. In this paper, the reliability of n-cascade system for k attacks with loss of m components has been derived for n > 4 and the general formula for reliability of n cascade system for k number of attacks has been derived. Using above general equation reliability has been calculated numerically for 6-cascade system for 2-number of attacks.
Cite this paper
NalaboluSwathi,Tallapureddy Sumathi UmaMaheswari, (2015) Reliability Analysis of a Redundant Cascade System by Using Markovian Approach. Journal of Applied Mathematics and Physics,03,911-920. doi: 10.4236/jamp.2015.37111
References
- 1. Kapur, K.C. and Lamberson, L.R. (1977) Reliability in Engineering Design. John Wiley and Sons, Inc., New York.
- 2. Shoomans, M.L. (1968) Probabilistic Reliability an Engineering Approach. McGraw-Hill, New York.
- 3. Schatz, R., Shooman, M. and Shaw, L. (1974) Applications of Time-Dependent Stress-Strength Models of Non-Electrical and Electrical Systems. Proceedings of Reliability and Maintainability Symposium, January 1974, 540-547.
- 4. Narahari Pandit, S.N. and Sriwastav, G.L. (1975) Studies in Cascade Reliability—I. IEEE Transactions on Reliability, R-24, 53-57. http://dx.doi.org/10.1109/TR.1975.5215330
- 5. Tadjett, W.J. (1978) Base Estimation of Reliability for Mixture of Life Distribution. SIAM Journal of Applied Mathematics, 34, 692-703. http://dx.doi.org/10.1137/0134058
- 6. Raghavachar, A.C.N. and Pattabhi Ramacharyulu, N.C. (1983) Survival Function under Stress Attenuation in Cascade Reliability. OPSEARCH, 20, 190-207.
- 7. Raghavachar, A.C.N., Kesava Rao, B. and Narahari Pandit, S.N. (1987) The Reliability of a Cascade System with Normal Stress and Strength Distribution. ASR, 2, 49-54.
- 8. Sinha, S.K. (1986) Reliability and Life Testing. Weiley Eastren, New Delhi.
- 9. Uma Maheswari, T.S. (1993) Reliability of Cascade System with Normal Stress and Exponential Strength. Micro Electronics Reliability, 33, 927-936. http://dx.doi.org/10.1016/0026-2714(93)90289-b
- 10. Uma Maheswari, T.S. (1993) Reliability Comparison of an n-Cascade System with the Addition of an n-Strength System. Micro Electronics Reliability, 33, 477-479.
http://dx.doi.org/10.1016/0026-2714(93)90313-N - 11. Uma Maheswari, T.S. (1994) Reliability of Single Stress under n-Strengths of Life Distribution. Micro Electronics Reliability, 34, 569-572. http://dx.doi.org/10.1016/0026-2714(94)90097-3
- 12. Rekha, A. and Chenchu Raju, V.C. (1999) Cascade System Reliability with Rayleigh Distribution. Botswana Journal of Technology, 8, 14-19.
- 13. Maya, T.N. (2007) On a Finite Mixture of Pareto and Beta Distributions. Ph.D. Thesis Submitted to Cochin University of Science and Technology, Kerala.
NOTES
*Corresponding author.







































