Received 4 August 2014; revised 5 September 2014; accepted 18 September 2014

ABSTRACT

The work deals with a mathematical model for real-time acoustic monitoring of material parameters of media in multi-state viscoelastic engineering systems continuously operating in irregular external environments (e.g., wind turbines in cold climate areas, aircrafts, etc.). This monitoring is a high-reliability time-critical task. The work consistently derives a scalar wave PDE of the Stokes type for the non-equilibrium part (NEP) of the average normal stress in a medium. The explicit expression for the NEP of the corresponding pressure and the solution-adequateness condition are also obtained. The derived Stokes-type wave equation includes the stress relaxation time and is applicable to gases, liquids, and solids.

Keywords:

Acoustic Monitoring, Gas, Liquid, or Solid, Acoustic Equation, Visoelastic Media, Stress Relaxation Time, Average Normal Stress, the Stokes-Type Wave Equation

1. Introduction

One of the applications of the acoustic-sensing technology is monitoring of material parameters of engineering systems continuously operating in irregular external environments. This type of the operation indicates that the monitoring must be regular (e.g., periodic) and in the real-time mode. Many problems in this area deal with the systems that are multi-state and viscoelastic in the following sense. A system comprises at least two spatial domains, each of which is occupied with an isotropic medium that is spatially homogeneous at equilibrium and is at one of the three states of matter: gaseous, liquid, or solid. In addition to that, the states of at least two of these spatial components are different, and the components are generally visoelastic.

The features of the considered systems and available mathematical models used for the system material parameter monitoring are further specified and discussed in more detail below.

a) The regular monitoring of material parameters is implemented by the non-invasive sensing of acoustic signals in one or more components of the system. The subsequent identification of the parameters is performed by using the sensed signals and the corresponding medium-specific acoustic models (e.g., [1] [2] ).

b) The regular real-time acoustic monitoring presents the sequence of the sensing cycles started at a series of time points and implemented with one or more sensors in the automatic mode. If, say, 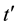and 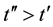are any two consecutive time points, the model-based processing of the sensed data received from all of the sensors must be completed unconditionally (e.g., without human intervention) during the time interval of the length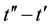. Otherwise, the data sensed in the 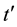-cycle will not be processed and, thus, will not contribute to the material parameter identification.

Moreover, the aforementioned continuous automatic operation presumes zero user intervention. This makes high demands of reliability of the data processing. The above picture indicates that the regular real-time moni- toring is a high-reliability time-critical task.

c) Due to the above multi-state feature of the system, the models mentioned in Point (a) generally include acoustic models for fluids and solids. In each of these cases, they are not formulated for acoustic signals, i.e. non-equilibrium parts of the Cauchy stress matrix entries. The fluid acoustic models are formulated for the entries of the velocity vector, whereas the solid acoustic models are formulated for the entries of the displace- ment vector. This inevitably complicates the entire description necessary for the parameter identification. More- over, the diversity and complexity of the modeling are further contributed by the use of representations for the conjunction of the initial conditions and the boundary conditions at the interfaces between the system com- ponents, which are at different states of matter (see above).

d) Acoustic models for fluids and solids generally include a system of three scalar non-stationary partial differential equations (PDEs) in the three-dimensional physical space.

e) Common fluid mechanics acoustic models natively include not only elastic moduli of the medium but also its viscosities, and thereby they are applicable to the corresponding viscoelastic components of the system. Also, the mentioned models are consistently derived from a more general physical theory, kinetic theory (e.g., [3] ) which, in turn, results form statistical mechanics (e.g., [4] ).

In contrast to that, common solid mechanics acoustic models include elastic moduli but do not include vis- cosities. There is an advanced model for visoelastic solids (e.g., [5] , (6.15)). It is based on the stress expression ( [5] , (6.14)), which is theoretically explained in ( [6] , §34), and includes both volume and shear viscosities of the medium. It appears to be a system of the Stokes-type wave PDEs. The term “Stokes-type” is due to the work of G.G. Stokes [7] .

However, as follows from the discussion in ( [6] , §34] (see also [5] , the text on (6.9), (6.14), and (6.15)), the advanced PDE system is a compound model. It is obtained by means of adding of the viscous stress to the inviscid/elastic stress. Thus, it is not derived consistently from more general physical theories. In this respect, the basis of the model has a significant heuristic content. As opposed to that, the Stokes equation [7] was derived consistently within theory of viscous fluids for the velocity potential.

The features of common acoustic continuum mechanics models listed in Points (c)-(e) are not well suited for the time-critical nature indicated in Point (b). Consequently, a modeling basis for regular real-time acoustic monitoring of material parameters of multi-state engineering systems continuously operating in irregular exter- nal environments remains a research topic. The purpose of the present work is to contribute to this topic. More specifically, the work derives an acoustic PDE for an appropriate scalar component of the Cauchy stress matrix and explains why this PDE is applicable to gases, liquids, and solids, including viscoelastic media.

It should be noted that the idea of PDEs for the entries of the Cauchy stress matrix goes back to at least H. Grad who derives non-stationary spatially non-homogeneous PDE system for these entries ( [3] , (28.19)). (The version of the system in the spatially homogeneous case is [3] , (28.22).) Nowadays, PDEs for the entries of the Cauchy stress matrix (or its other components) in fact form a new area in acoustic modeling because they allow concentrating attention directly on the quantities of the main interest in acoustics, without involvement of inter- mediate variables (such as the displacement vector in the case of solids or the velocity vector in the case of vis- cous fluids). This direction was contributed by other works. For instance, work [8] formulates the acoustic PDEs for all of the aforementioned entries in solids ([8] , the equation in the article “0138”). This feature allows [8] better focusing the models on sharp practical applications.

The work is arranged as follows. Section 2 summarizes the basic facts on the Cauchy stress matrix and the key component of it, scalar and deviatoric stresses. The main result derived in the work is presented in Section 3 that also discusses the novelty of it and its connection to the related results of other authors. Section 4 concludes the work. The detailed derivation of the main result is carried out in Appendix A. It applies selected represent- ations associated with the coupling of Eulerian and Lagrangian coordinates outlined in Appendix B.

2. Preliminaries: Scalar and Deviatoric Stresses

Acoustic signals present the spatiotemporal deviation, 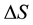, of the non-equilibrium part (NEP) of the Cauchy stress matrix, , of the medium from its equilibrium version,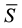

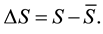(2.1)

The terms denoted with the sign “overline” are specified in the remark below.

Remark 2.1. As is well known, physical quantities at equilibrium are independent of time. The present work considers the media only such that, at equilibrium, they are independent of space as well. Consequently, the equilibrium versions of physical quantities do not depend on space either. These versions are denoted with the sign “overline” applied to the notation of the corresponding quantity (e.g., see (2.1)). ,

One usually represents matrix in the form of two components,

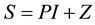(2.2)

where

(2.3)

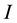is the identity 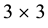-matrix, and 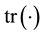is the trace of a matrix. As (2.3) shows, is a scalar variable and, thus, matrix PI in (2.2) presents the scalar stress.

The diagonal and off-diagonal entries of matrix S are known as the scalar normal and shear stresses, re- spectively. Since (2.3) determines P as the arithmetic mean of the total normal stresses, P is called the average normal stress (ANS).

As follows from (2.2) and (2.3), matrix is traceless, i.e. such that. For this reason, matrix

(2.4)

is called the deviatoric stress. Also, this stress is zero at equilibrium, i.e.

. (2.5)

The relaxation of deviatoric stress Z to its equilibrium value (2.5) is usually described in terms of the stress relaxation time, say, θ, and according to asymptotic representation. The stress relaxation exists in any material medium, in gases, liquids, and solids, no matter if the medium is spatially non-homogeneous or spatially homogeneous (e.g., see both [3] , (28.19) and [3] , (28.22) for the case of fluids).

In an isotropic medium, deviatoric stress explicitly depends on shear modulus of the medium, no matter if the latter is a solid (e.g., [5] , (1.43)) or a fluid (e.g., [9] , [10] , p. 655). In the case of a fluid, this depen- dence is presented implicitly, by means of the explicit dependence on shear viscosity of the medium.

For the sake of simplicity, we also use θ in the expression for volume viscosity where is the bulk modulus of the medium. Deviatoric stress does not depend on bulk modulus. The equilibrium versions of the mentioned equality is

(2.6)

Value and the equilibrium value of the mass density of the medium determine parameter

(2.7)

This parameter is sometimes called the speed of bulk waves.

We note that ANS P completely determines not only scalar stress PI but also the entire stress S at equilibrium with expression

(2.8)

that follows from (2.2) and (2.5). In view of of (2.2), (2.8), and (2.5), Expression (2.1) is equaivalent to

(2.9)

where

(2.10)

Remark 2.2. If the medium is close to the equilibrium state sufficiently in order to neglect deviatoric stress in (2.2), then (2.2) and (2.9) are reduced to and

(2.11)

respectively. ,

Some of the above relations are used in the derivation of the main result of the present work (see Appendix A).

3. The Stokes-Type Wave PDE for the Non-Equilibrium Part of the Average Normal Stress

As is shown in Appendix A, under the assumptions listed in Table 1, a closed description for the NEP of ANS is PDE

(3.1)

The derivation of (3.1) also provides the corresponding description for the NEP of pressure (see (A.1.11)), which is any of the following two relations

(3.2)

(3.3)

Equation (3.1) and any of (3.2) and (3.3) are linear. The corresponding solution-adequateness condition is (A.3.7) (see Proposition A.3.1).

In comparison with common wave PDE, PDE (3.1) includes an extra term, the one with stress relaxation time. This is a damping term. It, however, does not result from the choice of one or another damping model. On the contrary, it is consistently derived from the basic laws for continuum media (see Appendix A). The damping term represents the internal, viscous friction in the medium.

Remark 3.1. The derivation of model (3.1)-(3.3) follows theory of viscous fluids but admits the terms native

in theory of inviscid solids (see Remarks A.1.1 and A.2.1). Thus, the derived model is suitable for gases, liquids, and solids. ,

We also note a connection of PDE (3.1) to a special wave equation that was introduced in 1845. Formally, PDE (3.1) for NEP of ANS is identical to the Stokes wave PDE [7] for the velocity potential in a viscous fluid. Thus, (3.1) is one of the Stokes-type wave PDEs.

The Stokes-type wave PDEs for different variables are used in acoustic of viscoelastic solids since long ago. For example, Section 1 discusses the well-known Stokes-type wave PDE system for the displacement vector in a solid. Paper [11] analyzes propagation of plane and spherical waves in viscoelastic solids with the help of the normalized Stokes-type wave PDE, which is mathematically equivalent to (3.1). Book [12] discusses transient waves in gases, liquids, and solids in connection with applications to viscoelastic-solid acoustics in seismology. The entire modeling in this book is based on the Stokes wave PDE but treats its variable in a broader sense, as a generating function (e.g., [12] , (31) on p. 36). The in-depth discussion in ( [12] , the chapter “Epilogue”) em- phasizes a number of the advantages of the Stokes-type models.

4. Concluding Remarks

The present work considers material media, which are isothermal, spatially homogeneous and isotropic at equili- brium, with elastic properties treatable in terms of linear elasticity, and can be gaseous, liquid, or solid. The che- mical reactions and body forces in the media are neglected.

Under the assumptions listed in Table 1, the work consistently derives a scalar wave PDE (3.1) for the NEP of the ANS in the medium. Normal stress in any medium turns up in almost all situations, dynamic or not. Equation (3.1) appears to be a wave PDE of the Stokes type. It is endowed with the explicit expression for the NEP of the pressure, namely any of (3.2) and (3.3), and the solution-adequateness condition (A.3.7). This condition enables to check the adequateness of solutions of PDE (3.1). The derived model is applicable to media at different states of matter: gaseous, liquid, or solid (see Remark 3.1).

Application of the derived equation allows to overcome the difficulties emphasized in Points (c)-(e) in Section 1 and thereby meet requirements resulting from the high-reliability and time-critical nature formulated in Point (b) in the mentioned section.

Acknowledgements

The authors express their gratitude to the Swedish Energy Agency Project 37286-1 for a partial support of the present work. The authors also thank Anders Boström, the Head of the Division of Dynamics, Department of Applied Mechanics, Chalmers University of Technology, Gothenburg, Sweden, for a stimulating discussion.

References

Appendix A. Derivation of a Scalar PDE for the Non-Equilibrium Part of the Average Normal Stress

The purpose of this section is derivation of a description for the stress NEP (see (2.1) or (2.9)), which would include stress relaxation time. The derivation follows the line formulated in Section 1 and, therefore, is implemented in terms of viscous-fluid mechanics.

There are two approaches in continuum mechanics to modeling the space-time phenomena, Lagrangian and Eulerian (e.g., [13] , Sections 2.1 and 2.2). They are formally different but equivalent in the sense of mechanics. Eulerian coordinates are t and spatial vector x. Lagrangian coordinates are t and spatial vector y discussed in Appendix B.

Models for linear inviscid solids are based on Lagrangian approach (e.g., [14] , Section 1.8 on p. 142-143). They include both equilibrium elastic moduli and but do not include stress relaxation time.

Models for viscous fluids are based on Eulerian approach. They include volume and shear viscosities and, and, thus (see Section 2), not only both elastic moduli K and G but also stress relaxation time. Therefore, the derivation applies Eulerian approach.

According to Eulerian approach, a spatial point moving along a determinate trajectory is described with ODE

(A.1)

where is the time, , is the vector of the point position, and the vector of the point velocity depends not only on but also on,

(A.2)

The total time derivative of a scalar variable, which depends on time and space, is, in view of (A.1), expressed as follows

(A.3)

where column vector

(A.4)

is the gradient with respect to the entries of vector. Consequntly, is the corresponding divergence. Note the last term on the right-hand side of (A.3) is because of the -dependence in (A.2).

In view of Assumption 3 in Table 1, relation (2.9) is reduced to (2.11) that switches attention from to. The equation for the latter is derived below.

In view of Assumption 4 in Table 1, we confine ourselves with the equations for the laws of conservation of mass and momentum in the medium. They are formulated in terms of and the (volumetric) density of the momentum vector. Under Assumptions 2-6 in Table 1, the equations are of the following form (e.g., [13] , (3.1.3), (3.2.2); see also Remark 2.2)

(A.5)

(A.6)

We consider the quasi-equilibrium versions of these equations. These are the topics of Appendixes A.1 and A.2, respectively. In each of the two cases, the related inviscid/elastic-solid representations are indicated.

A.1. Quasi-Equilibrium Version of the Mass Conservation Law

The present section derives the quasi-equilibrium version of the mass conservation law (A.5). Quantity

(A.1.1)

is the NEP of. If

(A.1.2)

then (A.5) is reduced to its linearized version

(A.1.3)

The rest of this section concentrates on the terms and conditions, which assure inequality (A.1.2).

The equation of state for a viscous fluid is usually available in the following form

(A.1.4)

where and is the pressure and absolute temperature in the medium, respectively. As is well known, a fluid is an ideal gas if and only if is a linear function of at any fixed. Also, note that the equations of state in the form (A.1.4) are available for many solids. Two examples are the Birch equation and the Murnaghan equation. Equations of state are useful in describing the properties of fluids, mixtures of fluids, and solids. The case when the equation of state is not available for a solid is discussed in Remark A.1.1 below.

Assumption 4 in Table 1 allows to replace (A.1.4) with relation

(A.1.5)

Note that the derivative of this function with respect to is usually non-negative, i.e., determines the isothermal bulk modulus of the medium,

(A.1.6)

and, thus (see (2.7)), the isothermal version of,

(A.1.7)

We also note that, , and are determined as follows (cf., (A.1.5)-(A.1.7))

(A.1.8)

(A.1.9)

(A.1.10)

Equality (A.1.9) specifies (2.7) in terms of the equation of state (A.1.4).

The NEP of pressure,

(A.1.11)

is, due to (A.1.5) and (A.1.9), coupled with (A.1.1) as shown

(A.1.12)

By virtue of (A.1.12) and (A.1.10), inequality (A.1.2) is equivalent to

(A.1.13)

Since (A.1.13) holds because of Assumption 7 in Table 1, inequality (A.1.2) also holds. In view of this, non- equilibrium equation (A.5) is replaced with its linearized version (A.1.3).

Multiplying (A.1.3) by and taking into account (A.1.12) and (A.1.10), one obtains the following equi- valent form Equation (A.1.3)

(A.1.14)

Remark A.1.1. If the equation of state is unavailable for a solid, then representations (A.1.5)-(A.1.9) and (A.1.12) cannot be used. In this case, one can show that (A.1.13) is still valid (cf., Assumption 7 in Table 1) and derive (A.1.14) with the help of the well-known relation of theory of inviscid solids (e.g., [5] , (1.38))

(A.1.15)

where is the -vector counterpart of (A.4) (see (B.2) for vector). Indeed, application of operation (B.5) to (A.1.15) and substitution of (B.4) into the resulting equality leads to (A.1.14). Moreover, it follows from (A.1.15) and inequality (B.7) that inequality (A.1.13) holds. ,

We also note that Equation (A.1.14) can be rewritten as the expression for,

(A.1.16)

This equation is the quasi-equilibrium version of Equation (A.5), which is used below.

A.2. Quasi-Equilibrium Version of the Momentum Conservation Law

The present section derives the quasi-equilibrium version of the momentum conservation law (A.6). Owing to (A.5), equation (A.6) can be rewritten as or, equivalently, as

(A.2.1)

where is determined with (2.10).

Under Assumption 7 in Table 1, the momentum conservation law (A.6) is equivalent to its quasi-equilibrium version

(A.2.2)

Indeed, it is shown in Section A.1, that inequalities (A.1.13) and (A.1.2) are equivalent. Since, due to the aforementioned assumption, (A.1.13) is valid and inequality (A.1.2) is also valid. The latter fact and relation (A.1.1) enable one to replace in (A.2.1) with thereby resulting in (A.2.2).

Remark A.2.1. Quasi-equilibrium viscous-fluid equation (A.2.2) is equivalent to the well-known equation of inviscid solid mechanics (e.g., [5] , (1.15)) that, in the scalar-stress case (2.11), is of the following form

(A.2.3)

By virtue of (B.4) and (B.5), equation (A.2.2) can be transformed into

(A.2.4)

In view of (B.3) and (B.7),. Applying this equality to (A.2.3), one obtains (A.2.4). ,

Equation (A.2.2) is the quasi-equilibrium version of Equation (A.5), which is used below.

A.3. Derivation of the PDE

Equations (A.1.16) and (A.2.2) includes terms and, respectively. These terms are mutually coupled because of the well-known Stokes relation introduced 170 years ago (e.g., [14] , (12) on p. 140, [15] )

(A.3.1)

More specifically, due to (2.10), (A.1.11), and the fact that the equilibrium value of velocity is zero, (A.3.1) is specified to

(A.3.2)

Assumption 8 in Table 1 allows to replace this relation with a simpler one, namely

(A.3.3)

Applying (A.1.16) to (A.3.3) and taking into account expression in (2.6), one obtains

(A.3.4)

Application of operation to (A.1.16), substitution of (A.2.2) into the resulting equality, and allowing for (A.1.10) leads to

(A.3.5)

where. The latter, in view of (A.4), means that is the Laplace differential expression.

Assumption 9 in Table 1 enables one to simplify Equations (A.3.5) and (A.3.4) to

(A.3.6)

and (3.2).

Proposition A.3.1. Let vector, at which function is defined, be arbitrary fixed, be a time

interval, , and.

Then inequality (A.1.13) is valid at the above and uniformly in if

(A.3.7)

Proof. The proof is based on inequality, which follows from the hypothesis of the proposition, and the representation

(A.3.8)

for the solution of ODE (3.2) with initial value. ,

Since, as shown in Appendix A.1, (A.1.13) is equivalent (A.1.2) and the latter allows to reduce non-linear Equation (A.5) to its linearized version (A.1.3), the lenearization-enabling inequality (A.3.7) is in fact the solution-adequateness condition.

The obtained description for consists of equation system (3.2) and (A.3.6) for and . If solu- tion is available, then, according to Proposition A.3.1, it is adequate if the solution-adequateness condition (A.3.7) holds.

It is possible to transform system (3.2), (A.3.6) into the explicit expression for in terms of and the closed equation for. Indeed, as follows from (3.2), and hence

. Substitution of the latter equality into (A.3.6) transforms it into PDE (3.3) for. However, (3.3) is not a closed description for because it includes .

The closure is achieved in the following way. Applying (3.2) to (3.3), differentiating the resulting equality with respect to, and combining the outcome with (A.3.6), one obtains PDE (3.1) which is a closed description for.

As follows from the above derivation, Equations (3.2) and (3.3) are equivalent. Thus, they present the same equation in two different forms. Consequently, equation system (3.2), (A.3.6) is equivalently reduced to the following two relations: closed PDE (3.1) for and any of relations (3.2) and (3.3), which describe in terms of.

Appendix B. Auxiliary Summary on the Interrelation of Eulerian and Lagrangian Coordinates

As noted in Appendix A, the position of a spatial point in Eulerian coordinates is described with ODE (see (A.1), (A.2))

(B.1)

Let the spatial point at time be, i.e.

(B.2)

Then the displacement of the point at time and position is

(B.3)

where is the solution of ODE (B.1) under initial condition (B.2). Consequently,

(B.4)

Time t and position y constitute Lagrangian coordinates. Since y is independent of t (see (B.2)), Lagrangian version of Eulerian representation (A.3) is

(B.5)

In Lagrangian coordinates, the strain matrix is determined as follows

(B.6)

Note that

, in linear solids (B.7).

The rate of strain (B.6) is

that, after substitution of (B.4) into the right-hand side, becomes

(B.8)

In view of (B.7), relation (B.8) results in or, equivalently (see (B.6))

(B.9)

The Lagrangian-coordinate expressions for the time derivative, displacement, strain, rate of displacement, and rate of strain are (B.5), (B.3), (B.6), (B.4), and (B.9), respectively.

NOTES

^*Corresponding author.