Journal of Applied Mathematics and Physics
Vol.02 No.08(2014), Article ID:47579,11 pages
10.4236/jamp.2014.28086
Uniform Exponential Attractors for Non-Autonomous Strongly Damped Wave Equations
Hongyan Li
College of Management, Shanghai University of Engineering Science, Shanghai, China
Email: lihongyan580@sohu.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 May 2014; revised 3 June 2014; accepted 15 June 2014
ABSTRACT
In this paper, we study the existence of exponential attractors for strongly damped wave equations with a time-dependent driving force. To this end, the uniform Hölder continuity is established to the variation of the process in the phase apace. In a certain parameter region, the exponential attractor is a uniformly exponentially attracting time-dependent set in the phase apace, and is finite-dimensional no matter how complex the dependence of the external forces on time is. On this basis, we also obtain the existence of the infinite-dimensional uniform exponential attrac- tor for the system.
Keywords:
Exponential Attractor, Uniform Attractor, Strongly Damped Wave Equation

1. Introduction
In this paper, we study the following non-autonomous strongly damped wave equation on a bounded domain 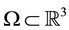 with smooth boundary
with smooth boundary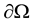 :
:
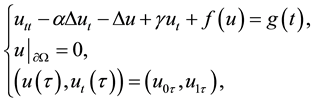 (1.1)
(1.1)
where 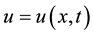 is a real-valued function on
is a real-valued function on 
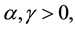
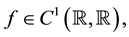

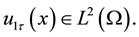 Let
Let 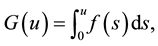 we make the following assumptions on functions
we make the following assumptions on functions 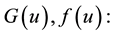
 (1.2)
(1.2)
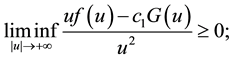 (1.3)
(1.3)
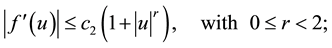 (1.4)
(1.4)
where 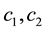 are positive constants. And we assume that the external force
are positive constants. And we assume that the external force 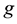 belongs to the space
belongs to the space 

for some given (possibly large) constant
Wave equations, describing a great variety of wave phenomena, occur in the extensive applications of mathe- matical physics. Equation (1.1) can be regarded as a perturbed equation of a continuous Josephson junction where



Recently, motivated by [6] , the authors have given a new explicit algorithm allowing to construct the expo- nential attractor, and this method makes it possible to consider more general processes in applications [10] [11] .
An exponential attractor 





In the present article, we study exponential attractors of the system (1.1) based on the concept of a non-au- tonomous (pullback) attractor. Thus, in the approach, an exponential attractor is also time-dependent. To be more precise, a family 

1) The fractal dimension of all the sets 
2) There exist a positive constant 





We emphasize that the convergence in (1.6) is uniform with respect to 
This article is organized as follows. In Section 2, we first provide some basic settings and show the absorbing and continuous properties in proper function space about Equation (1.1). In Section 3 and Section 4, we prove the existence of the uniform attractor and exponential attractor of Equation (1.1), respectively. Finally, we prove the existence of infinite-dimensional exponential attractor, and compare it with the non-autonomous exponential attractor in Section 5.
2. Preliminaries
We will use the following notations as that in Pata and Squassina [15] . Let 


and consider the family of Hilbert spaces 

Then we have
and the compact, dense injections
In particular, naming 

We recall the continuous embedding
and the interpolation results: given 


and let
Equation (1.1) is equivalent to the following initial value problem in the Hilbert space E

where 

It is well known (see, e.g., [3] , [9] ) that, under the above assumptions, Equation (2.1) possesses, for every 





Define a new weighted inner product and norm in 
for any
where 

Obviously, the norm 


Let
where 

and then the system (1.1) can be written as

where
Lemma 2.1 For any 
where

Proof. Since 


By (2.4) and (2.6), elementary computation shows
The proof is completed. ,
Lemma 2.2 Let assumptions (1.2)-(1.5) be satisfied. For any initial data


where 



Proof. Write 

value 



By (1.2), (1.3) and Poincaré inequality, there exist two positive constants 


By (2.4) and (2.6), 


where 
By Gronwall’s inequality, we have an absorbing property:
This completes the proof. ,
Theorem 2.1 Given any 


for some
The proof is similar to Theorem 2 in [15] . ,
Theorem 2.2 For the solutions of (2.5) with different external forces 



where 


The proof is similar to Lemma 4 in [5] .
3. Existence of the Uniform Attractor
The dissipativity property obtained in Lemma 2.2 yields the existence of an absorbing set for the process 



Theorem 3.1 The process 

Proof. We consider 

and we introduce the splitting 




and 

We now define the families of maps 


First step: We prove that 



where

Similar to Lemma 2.1, we have
where 


Similar to Lemma 2.2, applying (3.7) and Young, Poincaré, Gronwall inequalities, we obtain
Now we multiply (3.5) by 


with
Then from (3.8) we have
i.e.,

for the first term on the right-hand side of (3.9), we have

By (3.9), (3.10), and Lemma 2.2, there is 

let 

By (1.2), (1.3) and (2.8), (2.9), from (3.12), we obtain

Lemma 2.2 and (3.13) imply that 

Second step: Let


Multiply (3.3) by
due to Gronwall and Poincaré inequalities, then

Since the embedding 


Lemma 3.1 (see [16] ) Let 


with 




Third step: Let

Then from (3.15), Lemma 2.2, and the compactness of

It is easy to see that the process
defined by (2.5) has the following relation with

where 
Since the process 



4. Existence of Exponential Attractors
The main result of this section is the following theorem.
Theorem 4.1 Let the function f and the external force g satisfy the above assumptions. Then, for every ex- ternal force g enjoying (1.5), there exists an exponential attractor 
1) The sets 


where 

2) They satisfy a uniform exponential attraction property as follows: there exist a positive constant 





3) The sets 

where the constant 


4) The map 

where the positive constants 






where 



Proof. Firstly, we construct a family of exponential attractors for the discrete dynamical processes associated with Equation (2.5). According to Lemma 2.2, it only remains to construct the required exponential attractors for initial data belonging to the ball
where 








Lemma 4.1 Let the above assumptions on Equation (1.1) hold. Then, for every 

where the constant 




where 




Proof. Note that there is a 
and 


where all the constants depend on


Now, we can define the exponential attractors for continuous time by the following formula
with respect to 



for all



for a given



5. Infinite-Dimensional (Uniform) Exponential Attractor and Non-Autonomous Exponential Attractor
Finally, we compare the non-autonomous exponential attractor 
Let 



where 



Using the standard skew product flow in [4] and [5] , for every external forces 



It is known that 


It is also known that the uniform attractor 




Proposition 5.1 Let the above assumptions hold and the hull 





for some positive constants 


Definition 5.1 [11] [13] A set 
1) Entropy estimate: 



2) Semi-invariance: for every 


3) Uniform exponential attraction property: there exists a positive constant 




[13] points out that a uniform exponential attractor 

Theorem 5.1 Let the assumptions of Theorem 4.1 hold and let, in addition, the hull 

Remark 1 When



Equation (1.1) reduces to the damped wave equation modeling the Josephson junction in superconduction which was studied by many authors (see [1] [6] [17] ). We assume that the function 
Remark 2 When
if we assume that the function 
Acknowledgements
This work is supported by the National Natural Science Foundation of China (11101265) and Shanghai Edu- cation Research and Innovation Key Project of China (14ZZ157).
References
- Landahl, P.S., Soerensen, O.H. and Christiansen, P.L. (1982) Soliton Excitations in Josephson Tunnel Junctions. Phy- sical Review B, 25, 5337-5348.
- Dell’Oro, F. and Pata, V. (2012) Strongly Damped Wave Equations with Critical Nonlinearities. Nonlinear Analytical TMA, 75, 5723-5735. http://dx.doi.org/10.1137/0522057
- Ghidaglia, J.M. and Marzocchi, A. (1991) Longtime Behavior of Strongly Damped Nonlinear Wave Equations, Global Attractors and Their Dimension. SIAM Journal on Mathematical Analysis, 22, 879-895. http://dx.doi.org/10.1137/0522057
- Li, H. and Zhou, S. (2012) Kolmogorov ε-Entropy of Attractor for a Non-Autonomous Strongly Damped Wave Equation. Communications in Nonlinear Science and Numerical Simulation, 17, 3579-3586. http://dx.doi.org/10.1016/j.cnsns.2012.01.025
- Li, H. and Zhou, S. (2008) On Non-Autonomous Strongly Damped Wave Equations with a Uniform Attractor and Some Averaging. Journal of Mathematical Analysis and Applications, 341, 791-802. http://dx.doi.org/10.1016/j.jmaa.2007.10.051
- Prizzi, M. (2009) Regularity of Invariant Sets in Semilinear Damped Wave Equations. Journal of Differential Equations, 247, 3315-3337. http://dx.doi.org/10.1016/j.jde.2009.08.011
- Sun, C. (2010) Asymptotic Regularity for Some Dissipative Equations. Journal of Differential Equations, 248, 342- 362. http://dx.doi.org/10.1016/j.jde.2009.08.007
- Yang, M. and Sun, C. (2009) Dynamics of Strongly Damped Wave Equations in Locally Uniform Spaces: Attractors and Asymptotic Regularity. Transactions of the American Mathematical Society, 361, 1069-1101. http://dx.doi.org/10.1090/S0002-9947-08-04680-1
- Zhou, S. (1999) Global Attractor for Strongly Damped Nonlinear Wave Equations. Functional Difference Equations, 6, 451-470.
- Eden, A., Foias, C., Nicolaenko, B. and Temam, R. (1994) Exponential Attractors for Dissipative Evolution Equations. Research in Applied Mathematics, 37, John-Wiley, New York.
- Efendiev, M., Miranville, A. and Zelik, S. (2003) Infinite Dimensional Attractors for a Non-Autonomous Reaction- Diffusion System. Mathematische Nachrichten, 248-249, 72-96. http://dx.doi.org/10.1002/mana.200310004
- Chepyzhov, V.V. and Vishik, M.I. (2002) Attractors for Equations of Mathematical Physics. AMS College Publication, Providence.
- Efendiev, M., Zelik, S. and Miranville, A. (2005) Exponential Attractors and Finite-Dimensional Reduction for Nonautonomous Dynamical Systems. Proceedings of the Royal Society of Edinburg Sectection A, 135, 703-730.
- Miranville, A. (1998) Exponential Attractors for Non-Autonomous Evolution Equations. Applied Mathematical Letters, 11, 19-22. http://dx.doi.org/10.1016/S0893-9659(98)00004-4
- Pata, V. and Squassina, M. (2005) On the Strongly Damped Wave Equation. Communications in Mathematical Physics, 253, 511-533. http://dx.doi.org/10.1007/s00220-004-1233-1
- Atlas, A. (2005) Regularity of the Attractor for Symmetric Regularized Wave Equation. Communications on Pure and Applied Analysis (CPAA), 4, 695-704. http://dx.doi.org/10.3934/cpaa.2005.4.695
- Ogawa, T. and Takeda, H. (2011) Large Time Behavior of Solutions for a System of Nonlinear Damped Wave Equations. Journal of Differential Equations, 251, 3090-3113. http://dx.doi.org/10.1016/j.jde.2011.07.034
- Pata, V. and Zelik, S. (2006) Smooth Attractors for Strongly Damped Wave Equations. Nonlinearity, 19, 1495-1506. http://dx.doi.org/10.1088/0951-7715/19/7/001





















































