Journal of Applied Mathematics and Physics
Vol.2 No.4(2014), Article ID:43971,5 pages DOI:10.4236/jamp.2014.24006
Classification of All Single Traveling Wave Solutions to (3 + 1)-Dimensional Breaking Soliton Equation
Yang Li
Department of Mathematics, Northeast Petroleum University, Daqing, China
Email: liyang120918@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 February 2014; revised 10 March 2014; accepted 17 March 2014
ABSTRACT
In order to get the exact traveling wave solutions to nonlinear partial differential equation, the complete discrimination system for polynomial and direct integral method are applied to the considered equation. All single traveling wave solutions to the equation can be obtained. As an example, we give the solutions to (3 + 1)-dimensional breaking soliton equation.
Keywords
The Nonlinear Partial Differential Equation; Complete Discrimination System for Polynomial; Direct Integral Method; Traveling Wave Transform; (3 + 1)-Dimensional Breaking Soliton Equation

1. Introduction
For the past decades, to deal with nonlinear partial differential equations (PDEs), many methods have been developed. These methods have been widely applied to many PDEs to obtain the exact solutions. Recently, a method named the complete discrimination system for polynomial method has been proposed by Liu [1] -[5] . By Liu’s method, we can obtain the classification of single traveling wave solutions to some PDEs. For the PDE being considered, we take the traveling wave transformation and integrate it. The PDE can be directly reduced to ordinary differential equation (ODE) which can be turned into the integral form as follows:
 (1)
(1)
where 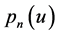 is a n-th order polynomial. By Liu’s method, we can obtain the classification of all solutions to the Equation (1).
is a n-th order polynomial. By Liu’s method, we can obtain the classification of all solutions to the Equation (1).
In this paper, we take into account (3 + 1)-dimensional breaking soliton equation, and it reads as
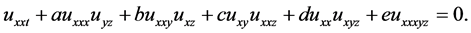 (2)
(2)
where a, b, c, d and e are arbitrary constants.
Equation (2) was originally proposed by Lin [6] to study the Virasoro-type symmetry algebra. Li [7] got some solitary wave solutions and periodic wave solutions of Equation (2) by using a simple transformation relation and solving the ordinary differential equation. Shi [8] gave some exact solutions of Equation (2) by turning it into KdV equation though introducing a simple transformation, and so on.
2. Classification
For Equation (2), we take the traveling wave transformation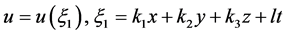 , and can obtain the corresponding reduced ODE as follow
, and can obtain the corresponding reduced ODE as follow
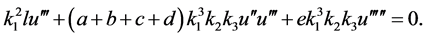 (3)
(3)
Integrating Equation (3) with respect to 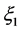 once , we simplify it and yield
once , we simplify it and yield
 (4)
(4)
where ![]() is an integral constant.
is an integral constant.
Let
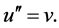 (5)
(5)
Then we have
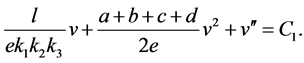 (6)
(6)
Or equivalently
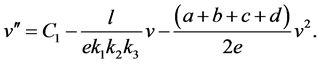 (7)
(7)
Integrating the Equation (7) once with respect to , we get
, we get
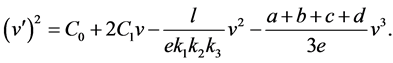 (8)
(8)
where 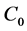 is an integral constant. For purpose of use the complete discrimination system for the third order polynomial, we have the following solving process.
is an integral constant. For purpose of use the complete discrimination system for the third order polynomial, we have the following solving process.
Let
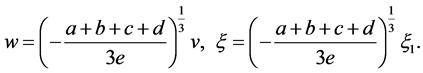 (9)
(9)
Then Equation (8) becomes
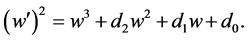 (10)
(10)
where ,
,  ,
, 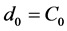 and
and 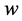 is a function of
is a function of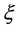 . The integral form of Equation (8) is
. The integral form of Equation (8) is
 (11)
(11)
Denote
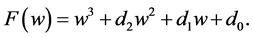 (12)
(12)
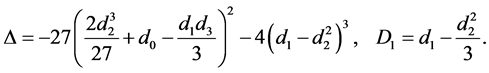 (13)
(13)
According to the complete discrimination system, we give the corresponding single traveling wave solutions to Equation (2).
Case 1.  has a double real root and a simple real root. Then we have
has a double real root and a simple real root. Then we have
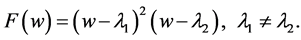 (14)
(14)
When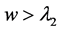 , the solutions to Equation (8) are as follows
, the solutions to Equation (8) are as follows
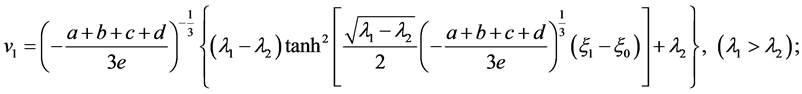 (15)
(15)
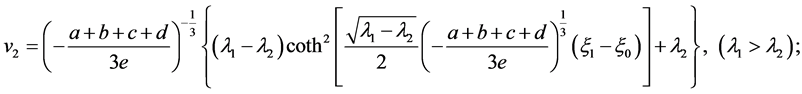 (16)
(16)
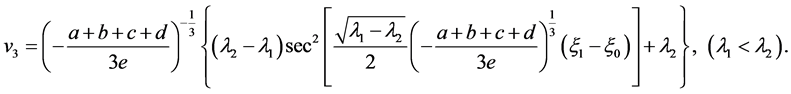 (17)
(17)
The corresponding solutions to Equation (2) are
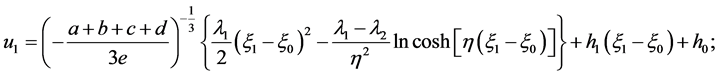 (18)
(18)
 (19)
(19)
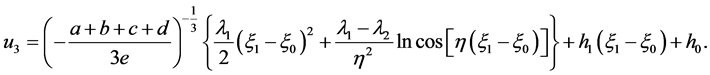 (20)
(20)
Case 2. 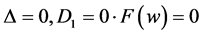 has a triple root. Then we have
has a triple root. Then we have
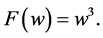 (21)
(21)
The corresponding solution to Equation (2) is
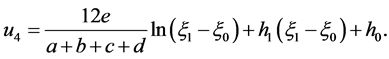 (22)
(22)
Case 3. 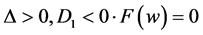 has three different real roots. Then we have
has three different real roots. Then we have
 (23)
(23)
When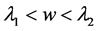 , the corresponding solutions to Equation (2) is
, the corresponding solutions to Equation (2) is
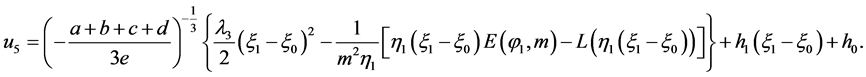 (24)
(24)
When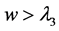 , the corresponding solutions to Equation (2) is
, the corresponding solutions to Equation (2) is
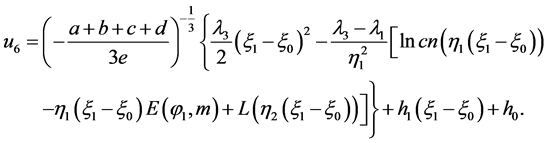 (25)
(25)
where .
.
Case 4. 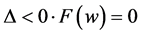 has only a real root. Then we have
has only a real root. Then we have
 (26)
(26)
When , the corresponding solutions to Equation (2) is
, the corresponding solutions to Equation (2) is
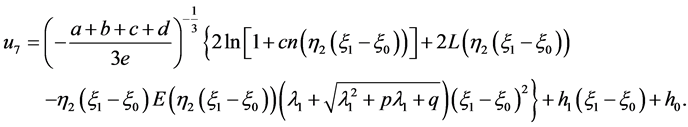 (27)
(27)
where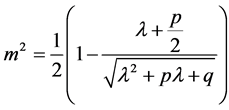 ,
, 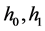 are integral constants in Equations (18)-(20), (22), (24), (25) and (27).
are integral constants in Equations (18)-(20), (22), (24), (25) and (27).
In Equations (24) (25) and (27), we give the expression of some signals as follow
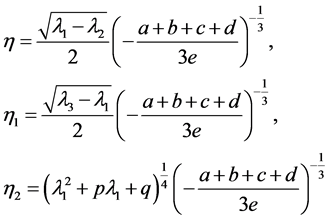 (28)
(28)
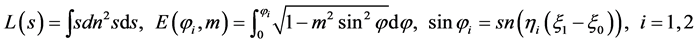 (29)
(29)
The solutions 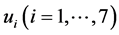 are all possible exact traveling wave solutions to Equation (2). We can see it is easy to write the corresponding solutions to (3 + 1)-dimensional breaking soliton equation.
are all possible exact traveling wave solutions to Equation (2). We can see it is easy to write the corresponding solutions to (3 + 1)-dimensional breaking soliton equation.
3. Conclusion
From the descriptions above, we use the complete discrimination system for polynomial and direct integral method to obtain all possible traveling wave solutions to (3 + 1)-dimensional breaking soliton equation. This method is direct and effective. With the same method, some of other equations can be dealt with.
Acknowledgements
I would like to thank the referees for their valuable suggestions.
References
- Liu, C.S. (2007) Classification of All Single Travelling Wave Solutions to Calogero-Degasperis-Focas Equation. Communications in Theoretical Physics, 48, 601-604. http://dx.doi.org/10.1088/0253-6102/48/4/004
- Liu, C.S. (2010) Applications of Complete Discrimination System for Polynomial for Classifications of Traveling Wave Solutions to Nonlinear Differential Equations. Computer Physics Communications, 181, 317-324. http://dx.doi.org/10.1016/j.cpc.2009.10.006
- Liu, C.S. (2008) Solution of ODE
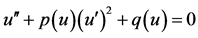 and Applications to Classifications of All Single Travelling Wave Solutions to Some Nonlinear Mathematical Physics Equations. Communications in Theoretical Physics, 49, 291-296. http://dx.doi.org/10.1088/0253-6102/49/2/07
and Applications to Classifications of All Single Travelling Wave Solutions to Some Nonlinear Mathematical Physics Equations. Communications in Theoretical Physics, 49, 291-296. http://dx.doi.org/10.1088/0253-6102/49/2/07 - Liu, C.S. (2006) All Single Traveling Wave Solutions to (3+1)Dimensional Nizhnok-Novikov-Veselov Equation. Communications in Theoretical Physics, 45, 991-992. http://dx.doi.org/10.1088/0253-6102/45/6/006
- Liu, C.S. (2008) Representations and Classification of Traveling Wave Solutions to Sinh-Gördon Equation. Communications in Theoretical Physics, 49, 153-158. http://dx.doi.org/10.1088/0253-6102/49/1/33
- Lin, J., Lou, S.-Y. and Wang, K. (2001) High-Dimensional Virasoro Integrable Models and Exact Solution. Physics Letters A, 287, 257-267. http://dx.doi.org/10.1016/S0375-9601(01)00488-1
- Li, H.-M. and Lou, S.-Y. (2002) The Analytical Solutions of (3 + 1)-Dimensional Breaking Soliton Model. Journal of Liaoning Nomal University (Natural Science Edition), 25, 23-26.
- Shi, Y.-R., Duan, W.-S., Lv, K.-P. and Yang, H.-J. (2004) Exact Solutions of (3 + 1)-Dimensional Breaking Soliton Equation. Journal of Liaoning Normal University (Natural Science Edition), 27, 155-157.

