Open Journal of Modern Hydrology
Vol.06 No.02(2016), Article ID:66183,13 pages
10.4236/ojmh.2016.62010
Spatio-Temporal Variation Analysis of Precipitation during 1960-2008 in the Poyang Lake Basin, China
Lifeng Yuan1,2,3, Guishan Yang3, Hengpeng Li3*, Zengxin Zhang4
1College of Geography & Biological Information, Nanjing University of Posts and Telecommunications, Nanjing, China
2USDA ARS, National Soil Erosion Research Laboratory, West Lafayette, IN, United States
3Key Laboratory of Watershed Geographic Sciences, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing, China
4Jiangsu Key Laboratory of Forestry Ecological Engineering, Nanjing Forestry University, Nanjing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
Long-term monthly precipitation data from 1960 to 2008 at 17 rain stations are analyzed to explore spatio-temporal variation of the seasonal and annual precipitation in the Poyang Lake basin, China, using anomaly analysis, simple linear regressive technique, Mann-Kendall trend test and Continuous Wavelet Transform. The results indicate that: (1) increasing precipitation trend is observed in summer and winter, while decreasing precipitation trend is identified in spring and autumn, and the above mentioned precipitation trends are not statistically significant; (2) changing trend of the areal average annual precipitation is non-significantly increasing, and increasing trend happens in almost the whole basin except in western and south-eastern small parts; (3) the spatial distribution of the seasonal and annual precipitation anomalies between 1991-2008 and 1960-2008 is similar to that of seasonal and annual precipitation trend during 1960-2008; (4) three main time-frequency distributions are observed in annual precipitation series during 1960- 2008, and they are 18 - 26 years, 8 - 14 years and 2 - 8 years, respectively; accordingly, there are three main periods in annual precipitation series, and they are 11-year, 22-year and 5-year respectively. This result will be helpful for further research on availability, scientific management and assessment of the water resources of the Poyang Lake basin.
Keywords:
Precipitation, Poyang Lake Basin, Mann-Kendall Trend Test, Continuous Wavelet Transform

1. Introduction
Precipitation estimation is an important and challenging task in hydrology because of high variability and changing climate [1] . In all factors of climatic and hydrological domain, the change of precipitation with increasing and decreasing trends has attracted more attention because the changing climate has caused catastrophic flood and drought events which have already caused disasters around the world to both nature and human beings [2] - [4] . Under the background of global warming, the change trend of the average annual precipitation in China is not much obvious, but the fluctuation in regional precipitation is pretty large [5] . Therefore, it can accurately reveal the influence of climate change on regional water resources through study of the regional precipitation, especially focusing on variation patterns and spatio-temporal distribution of precipitation at basin scale [6] [7] .
Poyang Lake (28˚22' - 29˚45'N, 115˚47' - 116˚45'E) is the largest freshwater lake in China, located at the middle reaches and southern bank of Yangtze River. The total drainage area of the water systems of the Poyang Lake basin is 1.62 × 105 km2, accounting for 9% of the drainage area of the Yangtze River basin and nearly 96.85% of the land area of Jiangxi Province [8] . The amount of areal average annual precipitation is above 1600 mm and is the richest area of precipitation in the Yangtze River basin. Monthly total precipitation of the Poyang Lake basin increases rapidly from January to June and then decreases sharply [9] . In the past half-century, due to intensive human activity and climate change, ecological environment and hydro-climate processes in the Poyang Lake basin have significantly changed, such as reservoir construction in five major rivers upstream [10] - [14] , levee construction surrounding lake area and land use and land cover change [15] [16] . Furthermore, with the increase of extreme weather events in recent years, it caused flood and drought disasters which occurred alternatively and frequently [11] [16] [17] . Hence, it is significantly important to identify and understand the variability characteristics and spatio-temporal distribution of precipitation in the Poyang Lake basin to protect regional resources and environment and keep the harmonious development of the economy and society.
In fact, there have been many studies focusing on the variation characteristic analysis of precipitation in the Poyang Lake basin. Guo et al. [18] analyzed trends and jumps of climate change in this basin based on observation data on temperature, precipitation and evaporation from 14 rain gauge stations from 1961 to 2003. Peng et al. [19] used time series anomaly analysis with rescaled range analysis which was based on fractal theory to discover the variation process of precipitation in this basin during the period of 1959-2005. Wang et al. [6] explored the change tendency of the total annual precipitation, rainfall days and rainstorm days by using liner regression and Mann-Kendall method. Huo et al. [20] analyzed long-term trends and persistence of precipitation based on the daily precipitation data of 10 meteorological stations in the Poyang Lake basin since 1950s. Zhang et al. [21] indicated precipitation and hydrological variations and related associations with large-scale circulation in this basin. Li et al. [22] identified the temporal variability of the past 60-year precipitation based on 3 rain gauge stations in this basin by using wavelet analysis. Zhang et al. [13] revealed changing properties, causes and topography-based spatial patterns of precipitation extremes in the Poyang Lake basin.
However, some problems still remain unanswered, e.g. what are the changing trends and spatial patterns of the seasonal and annual precipitation? what is possible the primary period and time-frequency variability distribution of the annual precipitation during the nearly 50 years? Because of the close correlation between precipitation and stream flow in the Poyang Lake basin, further research on seasonal and annual precipitation variability will be helpful for better understanding of the availability, scientific management and assessment of the water resources of the Poyang Lake basin.
The objectives of this paper are: (1) to detect the possible trends and the statistical significance of seasonal and annual precipitation data series in the Poyang Lake basin; (2) to explore the time-frequency distribution and the primary period of annual precipitation and identify the time turning point of a long-term annual precipitation series; and (3) to analyze the spatio-temporal distribution of seasonal and annual precipitation changes in the Poyang Lake basin during 1960-2008.
2. Data and Methods
2.1. Data
Long-term monthly precipitation data covering 1960 to 2008 at 17 rain gauge stations in the Poyang Lake basin are analyzed. Data were provided by the China Meteorological Data Sharing Service System (http://data.cma.cn/). The locations of the study area and the precipitation stations are shown in Figure 1.
Poyang Lake basin belongs to the subtropical monsoon climate zone, and precipitation exhibits distinct seasonality. For reflecting the variation trend of each seasonal precipitation separately, a year is divided into four seasons by the traditional climate division method, i.e. spring (March-May), summer (June-August), autumn (September-November), and winter (December-February). The areal average precipitation is calculated by the method of arithmetic average and 12 monthly precipitation data are summed to obtain the amount of precipitation for the year.
Data consistency check. There are a few missing data (1999-2006) for only the Ninggang station among 17 stations in monthly precipitation dataset. The missing precipitation data was filled in by the arithmetic average method, i.e. using the average value of its neighboring rain gauge stations. We consider that the gap filling method will have no influence on the long-term temporal trend. Finally, the total precipitation data for 49 years (1960-2008) in the Poyang Lake basin has been checked by the cumulative deviation method, and all data go through a 95% confidence level test (details see [23] ). Hence, it can be considered that time series of precipitation data are consistent before the Mann-Kendall trend test and the wavelet analysis.
2.2. Method
Four methods, namely, anomaly analysis, simple linear regression, Mann-Kendall (MK) trend test and Continuous Wavelet Transform (CWT), are used in the study to detect trends and variations of the seasonal and annual precipitation series in the Poyang Lake basin. Anomaly analysis method is applied to precipitation data pre-processing, and its results are used as input data in MK and CWT analysis. The simple linear regression is used to fit the seasonal and annual precipitation time series, a ten times slope of the fitting line denote the climate trend rate, which roughly indicate the variation value of precipitation over 10 years. This method is a parametric t-test method, which consists of two steps, fitting a linear simple regression equation with the time t as an independent variable (in this case monthly precipitation), Y, as a dependent variable, and testing the statistical significance of the slope of the regression equation. The parametric t-test requires that the data to be tested be normally distributed. The normality of the precipitation series is first tested in the study by applying the Kolmogorov-Smirnov test. The method first compares the specified theoretical cumulative distribution function (in our case normal distribution) with the sample cumulative density function based on observations, then calculates the maximum deviation, D. If, for the chosen significance level, the observed value of D is greater than or equal to the critical tabulated value of the Kolmogorov-Smirnov statistic, the hypothesis of normal distribution is rejected [4] [7] [24] . The MK test and simple linear regression is applied to detect the changing trend of precipitation
Figure 1. Location of the study area and precipitation gauging stations.
time series during 1960-2008 in Poyang Lake basin. In addition, The CWT analysis is used to distinguish periodicity properties of the precipitation time series during 1960-2008.
Mann-Kendall test. The rank-based Mann-Kendall method [25] [26] is a non-parametric and commonly used to assess the significance of monotonic trends in a hydro-meteorological time series [4] [21] [24] . The MK test considers only the relative values of all terms in the series 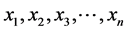 to be analyzed. For each term
to be analyzed. For each term 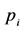 was computed as the number of later terms in the series whose value exceeds
was computed as the number of later terms in the series whose value exceeds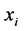 . Then the MK rank statistic
. Then the MK rank statistic 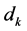 was given by:
was given by:
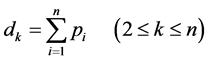 . (1)
. (1)
Under the null hypothesis of no trend, the statistic 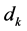 is distributed as a normal distribution with the expected value of
is distributed as a normal distribution with the expected value of 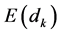 and the variance
and the variance 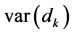 as follows:
as follows:
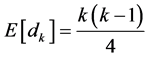 (2)
(2)
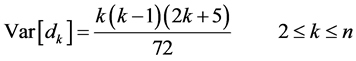 . (3)
. (3)
Under the above assumption, the definition of the statistic index 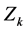 is calculated as:
is calculated as:
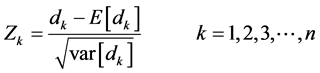 . (4)
. (4)
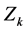 follows the standard normal distribution (here, we call it
follows the standard normal distribution (here, we call it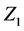 , and later we will get another
, and later we will get another











again following the procedure showed in Equations (1)-(4), then 



The results of the MK test are heavily affected by serial correlation of the time series [7] [24] . To eliminate the effect of serial correlation (if it is significant) on MK results, prewhitening has been applied to the MK test in the trend-detection studies of hydrological time series [29] .
Wavelet analysis. Wavelet analysis has recently been paid more attention to as a useful method and is widely applied in multi-scale analysis of the climate and hydrological research [30] - [33] . It can analyze multiple timescale characteristics of the signal sequence by scaling and translation of mathematic functions, and reflect local variations characteristics in a time series, and has the ability to diagnose the turning point. Compared to the Fourier transform, the wavelet transform analysis is considered to be more effective in studying non-stationary time series, such as climate and hydrological data time series.
Wavelet function is defined as [30] : assuming 



Then, 


For any function

where, a is scale factor, 

In this paper, the Morlet wavelet was used to identify the primary period of average annual precipitation in the Poyang Lake basin. Its basic form is given as follow:

where 
Wavelet variance. Taking an integral of the square of wavelet coefficients in the time domain could get the wavelet variance:

The process of wavelet variance with scale 
3. Results and Discussion
The results of the Kolmogorov-Smirnov test and the serial correlation analysis (not shown) reveal that the seasonal and annual precipitation series at the 17 stations in the Poyang Lake basin are mostly normally distributed. The precipitation series of a non-normal distribution are transformed to satisfy the normal distribution, such as log mathematic transformation. This means that the use of the MK trend test and wavelet analysis is warranted.
3.1. MK Trend Test of Precipitation Changes
The values calculated by the MK test algorithm are shown respectively by the solid point line and hollow point line in Figure 2. If the solid point line or hollow point line passes over the dashed line, it means there is a statistically significant trend of increasing or decreasing.
Spring precipitation changes. Figure 2(a) demonstrates the results of the MK trend analysis of spring precipitation with the Poyang Lake basin. The value of MK test of the spring data series is −0.81, which is not significantly decreasing. An increasing trend of the spring precipitation occurred during 1975-2004. After 2004, the spring precipitation shows a slightly decreasing trend, but far from being significant. The result of simple linear regression indicates a slightly downward trend (p > 0.05, not significant at >95% confidence level) for the spring precipitation series. Climate change trend rate of spring is −11.03 mm/10a.
Summer precipitation changes. The MK trend of summer precipitation is shown in Figure 2(b). The value of MK test of the summer precipitation series is 1.51, which is not significantly increasing. It is seen that 1969-1985 and 1994-2008 are featured by increasing trend of summer precipitation; 1963-1968 and 1986-1993 are dominated by decreasing trend of summer precipitation. The result of simple linear regression show an upward trend, but it is not significant (p > 0.05 not significant at >95% confidence level). The slope of fitting regression line is 2.512, which means climate trend rate of summer is 25.12mm/10a.
Autumn precipitation changes. Figure 2(c) show the MK trend of autumn precipitation. The value of the MK test of the autumn precipitation series is −0.97. Since 1963, the autumn precipitation shows a decreasing trend, but the value of MK test is less than −1.96 only at 1968. In general, the decreasing trend of autumn is not significant. The t-test result of the simple linear regression is 0.66 (p > 0.05 not significant at >95% confidence level), which indicates a slightly decreasing trend and also confirm the result of MK test. Climate trend rate of autumn is −4.16 mm/10a.



Figure 2. Mann-Kendall trend and simple linear regression analysis (parametric t-test) during 1960-2008 in spring ((a): March-May), summer ((b): June-August), autumn ((c): September-November), winter ((d): December-February) and the annual precipitation (e) of the Poyang Lake basin precipitation. The two horizontal dashed lines correspond to the confidence limits at the 5%-significance level (±1.96).
Winter precipitation changes. The MK trend of winter precipitation is plotted in Figure 2(d). The value of MK test of the winter precipitation series is 1.42, which is not significantly increasing. It is seen that the years 1964-2008 are dominated by the increasing trend of winter precipitation. The value of the MK test is greater than 1.96 only at 1975. As mentioned above, these changing trends are not significant. The result of simple linear regression indicates an upward trend (p > 0.05, not significant at >95% confidence level) for the spring precipitation series. Climate change trend rate of winter is 11.85 mm/10a.
Annual precipitation changes. Figure 2(e) shows the result of MK test for annual precipitation during 1960-2008. The value of MK test for annual precipitation series is 0.91, which denote not significantly increasing. It is seen that the years 1969-2008 is dominated by an increasing trend, especially 1998-2003 precipitation increasing trend is significant (MK value passes over the 95% confidence level line), and 1963-1968 is featured by a decreasing trend for annual precipitation. The result of the simple linear regression shows an upward trend, but it is not significant (p > 0.05 not significant at >95% confidence level). The slope of fitting regression line is 2.179, which denotes the climate trend rate of annual precipitation is 21.79 mm/10a.
As mentioned above, the results that an increasing precipitation trend is observed in summer, winter and per year, while decreasing precipitation trend identified in spring and autumn is consistent with precipitation change trend of the Yangtze river basin. Moreover, previous studies demonstrate that the Poyang Lake basin is the area where both precipitations in summer and extreme precipitation events most significantly increased in the Yangtze River basin in the past half century.
3.2. Continue Wavelet Analysis of Precipitation Changes
The continuous Morlet wavelet analysis is applied to a multiple timescale analysis of average annual precipitation of the Poyang Lake basin. The preprocessing of data is carried out by anomaly for filtering a one-year natural cycle of precipitation series before the wavelet transform. In addition, to eliminate the edge effect of wavelet analysis, precipitation series are extended toward both sides by the method of symmetric (whole-point) signal extend mode in Matlab software; after wavelet transformation, the extend part of wavelet coefficient are deleted to regain original wavelet coefficient.
The multiple time scale of annual precipitation. Multiple time scale characteristics of precipitation means that the change period of precipitation is different at the different time scales, which generally represent the small timescale cycle period and are often nested into the large timescale cycle period of precipitation. There are multiple levels of timescale structure and local variation features in time domain within precipitation changes over time.
Figure 3 shows the fluctuation characteristics of the real part time-frequency of the wavelet transform coefficients, which reflect an alternative variation of precipitation in the Poyang Lake basin. Positive wavelet coefficient corresponds to a more-than-normal period of precipitation; negative wavelet coefficient corresponds to a less-than-normal period of precipitation; wavelet coefficient is equal to zero which corresponds to the possible turning point of precipitation. Larger absolute value of a real part of the wavelet coefficient responds a more significant variation of timescale.
The fluctuation of timescale for 18 - 26 years, 8 - 14 years and 2 - 8 years are distinctly shown in Figure 3 in which positive and negative phases happened with an alternating pattern. In 18 - 26 years timescales, annual precipitation experiences 2.5 less-more cycle than normal alternative cycle; in 8 - 14 years timescales, annual precipitation experiences 4 more-less than normal alternative cycle; in 2 - 8 years timescales, annual precipitation experiences smaller alternative cycle. In addition, Figure 3 indicates that the maximum value of wavelet coefficient occurs at 1975 with the timescale of 22, 7, and 3 years, 1998 with the timescale of 22 years, and 2002 with the timescale of 4 years, demonstrating that the strongest fluctuation in annual precipitation is in 1975, 1998 and 2002. The same results can be observed from an annual precipitation of simple linear trend (Figure 2(e)). In fact, catastrophic floods disaster happened in 1975, 1998 and 2002 because of extreme precipitation events. In an intergeneration perspective, the 1960s, 1980s, and 2000-2008 are in the period of less than normal precipitation, the 1970s and 1990s are in the period of more than normal precipitation; and the contour of negative wavelet transformation coefficient doesn’t close yet at 2008, which denotes annual precipitation in the Poyang Lake basin will continue to decrease in the few years after 2008.
Figure 4 shows the modulus square time-frequency distribution under the 2 ~ 25 years timescale through the Morlet wavelet transformation, which represents the signal strength of characteristic timescales. There are three
Figure 3. Morlet wavelet real part of annual precipitation anomaly time series during 1960-2008. The warm color represents the positive phase (precipitation increasing) which means the coefficients of real part is greater or equal to 0.0; and the cold color indicates a negative phase (precipitation decreasing) which means coefficients of real part is less than 0.0.
Figure 4. Modulus square time-frequency distribution from Morlet wavelet transform coefficients.
primary timescales of fluctuation variation giving impact on annual precipitation. The timescale of 2 - 8 years and 18 - 26 years exhibit the strong signal whose oscillation center is respectively at 1972 (5-year timescale) and 1978 (22-year timescale), and happened before 1980 and 1985, respectively. The timescale of 8 - 14 years which primarily happened after 1985, and its oscillation center is at 2002 (11-year timescale).
The primary period of annual precipitation. The wavelet variance is applied to confirm the primary periods of annual precipitation series. The wavelet coefficients calculated are substituted into Equation (9) to calculate the wavelet variance of the annual precipitation anomaly series. The plot of wavelet transformation variance is drawn by 2 - 25 years timescale in Figure 5. The wavelet transformation variance reflects the energy of fluctuations with the distribution of timescale, those with stronger energy (peaks in Figure 5) are called the primary periods. Three peaks of the wavelet variance are marked in Figure5 whose values are located at the scale of 5- year, 11-year and 22-year. The apex value of wavelet variance of scale is 11-year which means the strong oscillation appears in an 11-year period. In addition, the second and third periods are 22-year and 5-year, respectively.
The turning point of annual precipitation change. From Figure 3 and Figure 4, it is seen that annual precipitation enters into a new oscillation cycle under either 22-year timescale or 11-year timescale in the beginning of 1990s, and annual precipitation exhibits an increasing trend. Meanwhile, wavelet coefficient value is equal to zero which denotes that turning point appears in that time. It can also be seen from Figure 2(e), while the MK value is positive and continues increasing from 1991 to 2002. To clearly illustrate the turning point of annual precipitation, cumulative annual precipitation anomaly is plotted in Figure 6, where cumulative anomaly started to increase from the beginning of 1991 to the end of 2002, and turned from a negative to positive value. Therefore, it can be deduced that the turning point of annual precipitation happened in about 1991.
3.3. Spatial Distribution of Seasonal and Annual Precipitation Changes
Figure 7 demonstrates the spatial distribution of the seasonal and annual precipitation in the Poyang Lake basin. In spring, the Poyang Lake basin is dominated by decreasing precipitation. Although a significant decreasing precipitation occurred in the western part of the Poyang Lake basin, the remainder of the Poyang Lake basin is dominated by a decreasing precipitation trend. Only four stations show an increasing trend. These were located in the south-western and northern parts (Figure 7(a)), but they are not significant.
The precipitation in summer shows an increasing trend (Figure 7(b)). In general, the middle and northern parts of the Poyang Lake basin show a significantly increasing trend and the remainder of the Poyang Lake basin is dominated by increasing precipitation trend. Only the south-eastern corner of the basin shows a decreasing trend.
Figure 5. Morlet wavelet transformation variance.
Figure 6. Cumulative annual precipitation anomaly during 1960-2008 in Poyang Lake basin.
Figure 7(c) indicates that the Poyang Lake basin is dominated by decreasing precipitation in autumn. The middle and northern part of the Poyang Lake basin show an increasing trend and the remainder of the Poyang Lake basin features a decreasing trend.
The precipitation changes in winter have similar patterns with those in summer. In winter, the Poyang Lake basin is totally dominated by an increasing precipitation trend (Figure 7(d)), the north, north-western and south- western parts are dominated by a significant increasing trend, and the remainder is dominated by an increasing precipitation trend.
For the annual precipitation changes (Figure 7(e)), the spatial distribution pattern of annual precipitation changes reflects a combined effect of the seasonal precipitation. The Poyang Lake basin is dominated by non- significantly increasing precipitation in most area of the basin, and the northern part show a significant increasing trend. Only the western and south-eastern two stations show a decreasing precipitation trend.
To demonstrate the precipitation changes between 1991-2008 and 1960-1990, precipitation anomalies of


Figure 7. Simple linear trend analysis of monthly precipitation during 1960-2008 in spring (a); summer (b); autumn (c); winter (d) and the annual precipitation (e) of the Poyang Lake basin precipitation.
1991-2008 and the last 30 years (1960-1990) were computed. Figure 8 demonstrates the precipitation anomalies between 1991-2008 and 1960-1990 (the difference of mean precipitation between 1991-2008 and 1960-1990). Figure 8(a) indicates that in spring the Poyang Lake basin is dominated by a negative precipitation anomaly, showing that less precipitation occurred during 1991-2008 compared to that during 1960-1990, although the north-western small part of the Poyang Lake basin shows an increasing trend of precipitation. Precipitation anomaly in summer (Figure 8(b)) shows that the Poyang Lake basin is totally dominated by a positive precipitation change in the season, which shows more precipitation occurred during 1991-2008 compared to that during 1960-1990. For the precipitation anomaly in autumn (Figure 8(c)), the Poyang Lake basin is dominated by negative precipitation changes in the almost the whole basin, showing a precipitation decreasing trend in the season during 1991-2008. In winter (Figure 8(d)), the Poyang Lake basin is dominated by a positive precipitation anomaly, especially in the north-western and south-western parts. The spatial distribution of precipitation anomalies between 1991-2008 and 1960-1990 shows that there is an obvious increasing in the northern and south- western part of Poyang Lake basin. The amount of precipitation during 1991-2008 is more than that during 1960-1990, although the general precipitation trend of the autumn and spring is decreasing which mainly happened at the south-eastern part of the basin. This phenomenon is similar to that obtained from simple linear trend analysis (Figure 2) and (Figure 7). The Poyang Lake basin is dominated by a positive precipitation anomaly


Figure 8. Precipitation anomaly between 1991-2008 and 1960-1990 in spring (a); summer (b); autumn (c); winter (d) and the annual precipitation (e).
(Figure 8(e)). The larger positive precipitation anomaly occurred mainly in the middle, northern and south- western part of the Poyang Lake basin.
4. Conclusions
Spatio-temporal variability and trends of the seasonal and annual precipitation of the Poyang Lake basin were studied with the method of the Mann-Kendall trend test, Continuous Wavelet Transform, simple linear regression and anomaly analysis. Some interesting conclusions are:
(1) Seasonal precipitation changes show that increasing trend mainly occurs in summer and winter; the precipitation in spring and autumn is dominated by decreasing trends in the Poyang Lake basin. The change trends of the seasonal precipitation are not significant in statistics. Furthermore, the increasing precipitation in summer and winter is found in the almost basin, and both summer and winter are similar patterns of the spatial distribution; the decreasing precipitation in spring is found in most of the area of the Poyang Lake basin except the south-western part and northern corner; in autumn, the decreasing precipitation is mainly found in the middle and northern Poyang Lake basin. The spatial distribution of the seasonal precipitation anomalies between 1991-2008 and 1960-2008 is similar to that of the seasonal precipitation trend. Positive precipitation anomaly happened in summer and winter in which larger positive precipitation mainly happened in the south-western and northern parts. A negative precipitation anomaly happened in spring and autumn in which a lesser negative precipitation anomaly mainly happened in the south-eastern parts.
(2) The spatio-temporal distribution of precipitation is very uneven because of the influence of climate abnormality and contour microclimate [18] . The changing trend of the average annual precipitation of the Poyang Lake basin is increasing, but it is not significant; the increasing trend happens in almost the whole basin except small parts of the western and south-eastern areas. The spatial distribution of the annual precipitation anomalies between 1991-2008 and 1960-2008 shows an increasing trend in the middle, northern and south-western parts and a decreasing trend in the south-eastern corner, which is similar to that of the average annual precipitation trend. The time-frequency analysis by Continuous Wavelet Transform indicates that there are three main time-frequencies in annual precipitation series during 1960-2008, and they are respectively for 18 - 26 years, 8 - 14 years and 2 - 8 years. Furthermore, three primary periods control the cycle alternation of the annual precipitation, and they are 11-year (first main period), 22-year (second main period) and 5-year (third main period), respectively. In addition, the turning point of annual precipitation series during 1960-2008 is at about 1991. With global warming, the hydrological cycle of the Poyang Lake basin will continue to accelerate, and spatio-tem- poral distribution of precipitation in the basin will become more uneven. The increase of precipitation in summer will cause a greater risk of floods disaster in the Poyang Lake basin in the future.
In this study, we have realized that it will produce more valuable results if we can collect longer precipitation data time series. In the future work, we will continue to collect longer precipitation series at this region to analyze precipitation period variation at longer time scale.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No.: 41001158, 41171020, 41271500), the National Basic Research Program of China (Grant No.: 2012CB417006), and by the Jiangsu Overseas Research & Training Program for University Prominent Young & Middle-aged Teachers and Presidents project.
Cite this paper
Lifeng Yuan,Guishan Yang,Hengpeng Li,Zengxin Zhang,1 1,1 1, (2016) Spatio-Temporal Variation Analysis of Precipitation during 1960-2008 in the Poyang Lake Basin, China. Open Journal of Modern Hydrology,06,115-127. doi: 10.4236/ojmh.2016.62010
References
- 1. Kalra, A. and Ahmad, S. (2011) Evaluating Changes and Estimating Seasonal Precipitation for Colorado River Basin Using Stochastic Nonparametric Disaggregation Technique. Water Resources Research, 47, 1-26.
http://dx.doi.org/10.1029/2010WR009118 - 2. Li, M., Xia, J., Chen, Z., Meng, D. and Xu, C. (2012) Variation Analysis of Precipitation during Past 286 Years in Beijing Area, China, Using Non-Parametric Test and Wavelet Analysis. Hydrological Processes, 27, 2934-2943.
http://dx.doi.org/10.1002/hyp.9388 - 3. Zhang, Q., Sun, P., Jiang, T., Tu, X. and Chen, X. (2011) Spatio-Temporal Patterns of Hydrological Processes and Their Responses to Human Activities in the Poyang Lake Basin, China. Hydrological Sciences Journal, 56, 305-318.
http://dx.doi.org/10.1080/02626667.2011.553615 - 4. Zhang, Z., Zhang, Q. and Jiang, T. (2007) Changing Features of Extreme Precipitation in the Yangtze River Basin during 1961-2002. Journal of Geographical Sciences, 17, 33-42.
http://dx.doi.org/10.1007/s11442-007-0033-x - 5. Ren, G., Guo J., Xu M., Chu Z., Zhang L., Zou X., et al. (2005) Climate Changes of China’s Mainland over the Past Half Century. Acta Meteorologica Sinica, 63, 942-955.
- 6. Wang, H., Zhao, G., Peng, J. and Hu, J. (2009) Precipitation Characteristics over Five Major River System of Poyang Drainage Area in Recent 50 Years. Resources and Environment in the Yangtze Basin, 18, 615-619.
- 7. Zhang, Q., Liu, C., Xu, C.Y., Xu, Y. and Jiang, T. (2006) Observed Trends of Annual Maximum Water Level and Streamflow during Past 130 Years in the Yangtze River Basin, China. Journal of Hydrology, 324, 255-265.
http://dx.doi.org/10.1016/j.jhydrol.2005.09.023 - 8. Sun, S., Chen, H., Ju, W., Yu, M, Hua, W. and Yin, Y. (2014) On the Attribution of the Changing Hydrological Cycle in Poyang Lake Basin, China. Journal of Hydrology, 514, 214-225.
http://dx.doi.org/10.1016/j.jhydrol.2014.04.013 - 9. Yuan, L., Yang, G., Li, H. and Zhang, Z. (2014) Rainfall Multiple Time Scale Variation Rule of Poyang Lake Basin in the Past 50 Years. Resources and Environment in the Yangtze Basin, 23, 434-440.
- 10. Guo, H., Su, B., Wang, Y. and Jiang, T. (2007) Runoff Coefficients Change and the Analysis of the Relationship between Climate Factors and Runoff Coefficients in Poyang Lake Basin (China): 1955-2202. Journal of Lake Science, 19, 163-169.
http://dx.doi.org/10.18307/2007.0209 - 11. Shu, X., Liu, Y. and Xiong, X. (2001) Ecological Environment Factors of Flooding Disasters and Countermeasures of Reducing Disasters in Poyang Lake Region. Journal of Jiangxi Normal University, 25, 181-185.
- 12. Ye, X., Zhang, Q., Bai, L. and Hu, Q. (2010) A Modeling Study of Catchment Discharge to Poyang Lake under Future Climate in China. Quaternary International, 244, 221-229.
http://dx.doi.org/10.1016/j.quaint.2010.07.004 - 13. Zhang, Q., Xiao, M., Li, J., Singh, V.P. and Wang, Z. (2014) Topography-Based Spatial Patterns of Precipitation Extremes in the Poyang Lake Basin, China: Changing Properties and Causes. Journal of Hydrology, 512, 229-239.
http://dx.doi.org/10.1016/j.jhydrol.2014.03.010 - 14. Guo, H., Hu, Q. and Jiang, T. (2008) Annual and Seasonal Streamflow Responses to Climate and Land-Cover Changes in the Poyang Lake Basin, China. Journal of Hydrology, 355, 106-122.
http://dx.doi.org/10.1016/j.jhydrol.2008.03.020 - 15. Shankman, D. and Liang, Q. (2003) Landscape Changes and Increasing Flood Frequency in China’s Poyang Lake Region. The Professional Geographer, 55, 434-445.
http://dx.doi.org/10.1111/0033-0124.5504003 - 16. Liu, J., Zhang, Q., Xu, C. and Zhang, Z. (2009) Characteristics of Runoff Variation of Poyang Lake Watershed in the Past 50 Years. Tropical Geography, 29, 213-218.
- 17. Shankman, D., Keim, B.D. and Song, J. (2006) Flood Frequency in China’s Poyang Lake Region: Trends and Teleconnections. International Journal of Climatology, 26, 1255-1266.
http://dx.doi.org/10.1002/joc.1307 - 18. Guo, H., Jiang, T., Wang, G., Su, B. and Wang, Y. (2006) Observed Trends and Jumps of Climate Change over Lake Poyang Basin, China: 1961-2003. Journal of Lake Science, 18, 443-451.
http://dx.doi.org/10.18307/2006.0501 - 19. Peng, R., Huang, H. and Zheng, L. (2009) The Persistence of Precipitation Series at Different Time Scales in Poyang Lake Region and Effective Measures to Reduce Socio-Economic Loss. Resources Science, 31, 731-742.
- 20. Huo, Y., Wang, L., Chen, X. and Meng, H. (2011) Long-Term Trend and Persistence of Precipitation over Lake Poyang Basin since 1950s. Journal of Lake Sciences, 23, 454-462.
http://dx.doi.org/10.18307/2011.0320 - 21. Zhang, Q., Liu, Y., Yang, G. and Zhang, Z. (2011) Precipitation and Hydrological Variations and Related Associations with Large-Scale Circulation in the Poyang Lake Basin, China. Hydrological Processes, 25, 740-751.
http://dx.doi.org/10.1002/hyp.7863 - 22. Li, R., Wang, P. and Wu, D. (2012) Wavelet Analysis of Annual Precipitation Series in Poyang Lake Basin. Journal of China Hydrology, 32, 29-31, 79.
- 23. Yuan, L., Zhang, Z., Liu, X. and Jiang, Z. (2013) Rainfall Sequence Consistency Test and Analysis of Poyang Lake Basin in Past 49 Years. Journal of Anhui Agricultural Sciences, 41, 732-735.
- 24. Chen, Y.D., Zhang, Q., Lu, X., Zhang, S. and Zhang, Z. (2011) Precipitation Variability (1956-2002) in the Dongjiang River (Zhujiang River Basin, China) and Associated Large-Scale Circulation. Quaternary International, 244, 130-137.
http://dx.doi.org/10.1016/j.quaint.2010.08.013 - 25. Kendall, M.G. (1975) Rank Correlation Methods. Oxford University Press, Oxford.
- 26. Mann, H.B. (1945) Nonparametric Tests against Trend. Econometrica, 13, 245-259.
http://dx.doi.org/10.2307/1907187 - 27. Ye, X., Zhang, Q., Liu, J., Li, L. and Guo, H. (2009) Impacts of Climate Change and Human Activities on Runoff of Poyang Lake Catchment. Journal of Glaciology and Geocryology, 31, 835-841.
- 28. Zhang, Q., Sun, P., Chen, X. and Jiang, T. (2011) Hydrological Extremes in the Poyang Lake Basin, China: Changing Properties, Causes and Impacts. Hydrological Processes, 25, 3121-3130.
- 29. Haan, C.T. (2002) Statistical Methods in Hydrology. Second Version, Iowa State Press, Iowa City.
- 30. Torrence, C. and Compo, G.P. (1998) A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, 79, 61-78.
http://dx.doi.org/10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 - 31. Labat, D. (2010) Cross Wavelet Analyses of Annual Continental Freshwater Discharge and Selected Climate Indices. Journal of Hydrology, 385, 269-278.
http://dx.doi.org/10.1016/j.jhydrol.2010.02.029 - 32. Nakken, M. (1999) Wavelet Analysis of Rainfall-Runoff Variability Isolating Climatic from Anthropogenic Patterns. Environmental Modelling & Software, 14, 283-295.
http://dx.doi.org/10.1016/S1364-8152(98)00080-2 - 33. Niu, J. and Sivakumar, B. (2013) Scale-Dependent Synthetic Streamflow Generation Using a Continuous Wavelet Transform. Journal of Hydrology, 496, 71-78.
http://dx.doi.org/10.1016/j.jhydrol.2013.05.025 - 34. Farge, M. (1992) Wavelet Transforms and Their Applications to Turbulence. Annual Review of Fluid Mechanics, 24, 395-457.
http://dx.doi.org/10.1146/annurev.fl.24.010192.002143 - 35. Li, M., Xia, J. and Meng, D. (2012) Long-Term Trend Analysis of Seasonal Precipitation for Beijing, China. Journal of Resources and Ecology, 3, 64-72.
NOTES
*Corresponding author.









