World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:61011,6 pages
10.4236/wjet.2015.34021
Model of Maintenance Planning Based on Trend of Machines Failures with Two Priorities
Erik Prada1, Alena Pešková2, Michael Valášek3
1Vehicle Center of Sustainable Mobility, Faculty of Mechanical Engineering, Czech Technical University in Prague, Prague, Czech Republic
2Department of Production Systems, Faculty of Mechanical Engineering, Technical University of Košice, Košice, Slovakia
3Faculty of Mechanical Engineering, Czech Technical University in Prague, Prague, Czech Republic

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 13 August 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT
In this article we are discussing the suggestion of planning maintenance in such situation that we have failures in database of failures and maintenance registered also according to type of failure― priority or non-priority. We are assuming that maintenance must be mainly oriented on avoiding major failures of machines. The effect of maintenance manifests with delay and is dependent on development of failures. We express this problem as linear programming task that is solvable with Solver-extension of application Excel. We demonstrate the suggested solution on example of failures of machines between years 2010 and 2012.
Keywords:
Microsoft Excel, Supplement Solver, Maintenance Planning, Priority and Non-Priority Failures, Linear Programming

1. Introduction
In the paper [1] we discussed the possibility of using a linear model of maintenance planning, which was based on the trend of failures. This model was designed and solved in Excel. Computer experiments showed that there was a need to deal with planned preventive maintenance and also priority of failure. We often register failures on the basis of character―priority resp. non-priority failure in the database of failures. We assume that maintenance must be oriented mainly to prevent priority failures of machines. Effect of maintenance manifests with a delay and it is dependent on trend of development failure in the last two periods.
Excel and its supplement Solver present also suitable tools for solving our problem in this case. Range of the problem allows its solution in real time. We will demonstrate our solution on illustrated example with these following parameters: we have 285 records of machine failures, of which 203 records are records about the way of machine failure. We need triplet of data (YEAR, MONTH, and LOSS) to create the input data, similarly as in the model [1] . Moreover, we need to specify whether the records deal with failure (priority, non-priority) or maintenance.
But specifying priority of failures may be a problem. One of the possibilities is to create a frequency table from failure code list, which represents the number of occurrences of the considered failure in watched period. Then we can sort this table in descending order and declare the first x failures as a priority. This approach has a logical reasoning as we preferably try to look after those machines that show increased rate of failure [2] [3] .
We’ve created a table of frequencies of failures in single months and in years 2010-2012 and based on it we have created graphs of the development of priority failures (Figure 1) and non-priority failures (Figure 2) and of development of preventive maintenance (Figure 3) that is realized.
By summarizing the above mentioned frequencies we get a table that allows us to determine the exact number of maintenance which is done in each month and their impacts on the identified priority and non-priority failures. We have part of the data in table (Table 1).
More informative than the table is the following chart of development of failures and maintenance. We see that preventive maintenance avoids failures relatively poorly and certainly not prioritized ones (Figure 4).
Figure 1. Development of priority failures.
Figure 2. Development of non-priority failures.
Figure 3. Development of maintenance.
Figure 4. Graphs of total number of failures and maintenance schedules.
2. Linear Programming Model
The following model tries to remove the above present disadvantage. Let pi1 priority failures and pi0 non- priority failure be identified during n-periods and it ui maintenance schedules (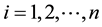 ) was realized. It is assumed that the period consists of t cycles i.e. n = r × t.
) was realized. It is assumed that the period consists of t cycles i.e. n = r × t.
We are looking for such plan of maintenance schedules xi, where the sum of coefficient of efficiency from maintenance priority machines yi and coefficient of efficiency from maintenance from non-priority machines is maximal [4] -[6] .
Variables are integer values xi in this model, that indicate the number of planned maintenance in the i-th period, which reflects preference of maintenance cause of priority failure. Coefficient of maintenance efficiency y1 can be interpreted as a percentage from the number of failures, that have to be covered by priority mainten- ance in that same month.
We are getting to the following task of linear programming:
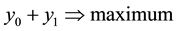 (1)
(1)
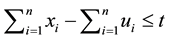 (2)
(2)
Table 1. Total number of failures and maintenance schedules.
 (3)
(3)
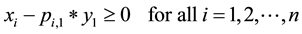 (4)
(4)
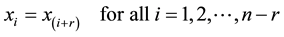 (5)
(5)
 (6)
(6)
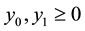 (7)
(7)
The target function “Equation (1)” maximizes total coefficient of maintenance efficiency. Restrictive condition “Equation (2)” ensures that the number of preventive maintenance in the cycle is greater than the number of already performed maintenance. Restriction “Equation (3)” ensures that the number of non-priority failures in the current period will be covered by efficiency taken from preventive maintenance in the previous and current periods. Restriction “Equation (4)” provides the same coverage of non-priority failures only at the current period. Cycles in periods are formulated by restriction “Equation (5)” Conditions “Equation (6)” and “Equation (7)”are forced by character of variables [7] -[9] .
Before using the Excel Solver it is necessary to define the cells of the worksheet on the basis of conditions “Equation (1)”-“Equation (7)”of the model (Table 2).
Results of this solution are shown in (Figure 5).
We are getting y0 = 0.31 and y1 = 0.50 which leads to an overall average efficiency of 40.62%.
3. Summary
Computer experiment with the presented model “Equation (1)”-“Equation (7)” has shown its applicability to real data. Solver of linear programming in Excel allows optimal scheduling of preventive maintenance that will be used for the benefit of preventing the priority failures as much as possible. Moreover it offers also a quantita-
Figure 5. Graph after optimization.
Table 2. Optimization in excel.
tive computing the effectiveness of these maintenances. We believe that if we will know also other parameters, for example average expense for maintenance, removal priority resp. non-priority failures or total financial source we will be able to generalize this more in the economic aspect. We will see limitations of the presented model in larger size of data that Excel can no longer process. Then it is appropriate to use other software to optimize, for example Gurobi optimization. For practical use of our proposed model it is necessary to determine more priorities.
Acknowledgements
This publication was supported by the European social fund within the framework of realizing the project “Support of inter-sectoral mobility and quality enhancement of research teams at Czech Technical University in Prague”, CZ.1.07/2.3.00/30.0034 and the contribution has been elaborated within the task solution: “E-learning of robotics with the implementation of virtual laboratory with remote control of real facilities on based Internet”.
Cite this paper
ErikPrada,AlenaPešková,MichaelValášek, (2015) Model of Maintenance Planning Based on Trend of Machines Failures with Two Priorities. World Journal of Engineering and Technology,03,205-210. doi: 10.4236/wjet.2015.34021
References
- 1. Pesková, A. (2013) Linear Model of Maintenance Planning Based on Failure Trend of Equipments in Excel. Trends and Innovative Approaches in Business Processes: 16. International Scientific Conference, Technical University of Kosice, Kosice, 7-8 November 2013, 1-6.
- 2. Harmon, M. (2013) Step-By-Step Optimization with Excel Solver—The Excel Statistical Master. Excel Master Series, Kindle Edition, Amazon Digital Services.
- 3. Ragsdale, T.C. (2011) Spreadsheet Modeling and Decision Analysis. 6th Edition, Cengage Learning, South-Western.
- 4. Dantzig, G.B. (1963) Linear Programming and Extensions. Princeton University Press, Princeton.
- 5. Chandrakantha, L. (2012) Using Excel Solver In Optimization Problems. John Jay College of Criminal Justice of CUNY, New York.
- 6. Meissner, J. and Nguyen, T. (2008) An Introduction to Spreadsheet Optimization Using Excel Solver. Lancaster University, Lancaster.
- 7. Gmiterko, A., Prada, E., Virgala, I., Surovec, R. and Vacková, M. (2011) Comparison of Neural Networks Learning Algorithms for Simulation of Rectilinear Snake Locomotion. Modelling of Mechanical and Mechatronic Systems 2011.
- 8. Prada, E., Virgala, I., Granosik, G., Gmiterko, A. and Mrkva, S. (2014) Simulation Analysis of Pneumatic Rubber Bellows for Segment of Hyper-Redundant Robotic Mechanism. Applied Mechanics and Materials, 611, 10-21.
- 9. Lipták, T., Gmiterko, A., Kelemen, M., Virgala, I., Prada, E. and Menda, F. (2014) The Use of Geometric Mechanics Concept at Kinematic Modeling in Mobile Robotics. Procedia Engineering, 96, 273-280.
http://dx.doi.org/10.1016/j.proeng.2014.12.154







