World Journal of Engineering and Technology
Vol.02 No.04(2014), Article ID:51565,6 pages
10.4236/wjet.2014.24031
A Proposed Exercise to Reinforce Abstract Thinking for Upper-Division Computer and Electrical Engineering Students: Modeling a High-Speed Inverter Using Cognitive Representations and Abstract Algebra
Robert Melendy
School of Engineering and Computational Sciences, Liberty University, Lynchburg, USA
Email: rfmelendy@liberty.edu
Academic Editor: Abdullah M. Al-Shaalan, Electrical Engineering Department, College of Engineering, King Saud University, KSA
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; revised 11 October 2014; accepted 12 November 2014
ABSTRACT
In mathematics, physics, and engineering, abstract concepts are an indispensable foundation for the study and comprehension of concrete models. As concepts within these fields become increas- ingly detached from physical entities and more associated with mental events, thinking shifts from analytical to conceptual-abstract. Fundamental topics taken from the abstract algebra (aka: mod- ern algebra) are unquestionably abstract. Historically, fundamental concepts taught from the ab- stract algebra are detached from physical reality with one exception: Boolean operations. Even so, many abstract algebra texts present Boolean operations from a purely mathematical operator perspective that is detached from physical entities. Some texts on the abstract algebra introduce logic gate circuits, but treat them as perceptual symbols. For majors of pure or applied mathemat- ics, detachments from physical entities is not relevant. For students of Computer and Electrical Engineering (CpE/EE), mental associations of Boolean operations are essential, and one might argue that studying pure Boolean axioms are unnecessary mental abstractions. But by its nature, the CpE/EE field tends to be more mentally abstract than the other engineering disciplines. The depth of the mathematical abstractions that we teach to upper-division CpE/EE majors is certainly up for questioning.
Keywords:
Abstract thinking, sensorimotor Reenactment, Neurocognition, microelectronics, Boolean Algebra

1. Introduction
In traditional computer and electrical engineering curricula, juniors must complete a course sequence in micro- electronic devices and circuits (often referred to as microelectronics or electronic circuits). Depending on the academic institution, this sequence is typically two semesters or three trimesters in duration. Classic textbooks may include [1] -[4] .
One of the successions of topics covered in this sequence is digital circuits, which includes a meticulous study of the dynamic switching characteristics of a basic metal-oxide semiconductor field-effect transistor (MOSFET) inverter. Prior to this juncture, students have to spend several weeks learning about the comprehensive physical structure and current-voltage characteristics of these devices, followed by how MOSFETs are biased to operate as linear amplifiers. Preceding the microelectronics sequence, CpE/EE majors traditionally complete a course in digital logic design. This is where the student learns about fundamental binary and hexadecimal arithmetic opera- tions, the basic logic gates as mathematical operators, the various transistor-transistor logic (TTL) gate IC fami- lies, their combinational and sequential switching architectures, hardware reduction techniques, and hardware description language (e.g., VHDL, [5] ).
When CpE/EE juniors are ready to study digital circuit configurations in microelectronics, they first should learn how an inverter circuit is formed using discrete components. This is initially introduced as resistor-transis- tor logic (RTL), followed by the complementary MOS (CMOS) configuration. It’s here where students’ know- ledge of 1) transistor i-v characteristic curves; 2) TTL logic gates, gets unified. Students learn that a MOSFET must be operated in either the cutoff or triode regions if it’s to function as a logic inverter. Rather than using theoretical “1 s” and “0 s” to represent logic states, students acknowledge that these binary representations are distinctive [6] objects: dc voltages measured at the gate and drain terminals of a CMOS pair. Concurrently, stu- dents establish that these voltages are restricted to the extreme and ideal limits of zero (e.g., VOL) or some “full” amount (e.g., VOH), and that these voltages represent MOSFET operation in the cutoff and triode regions, respec- tively. What’s more, the student learns that the switching transition from VOL to VOH (and vice versa) is not instantaneous, and that there are tangible energy consequences for such an ideality. It’s at this critical juncture that the student experiences sensorimotor reenactment [7] [8] and an elaboration of abstract concepts [9] [10] .
Simultaneously, students learn that familiar MOSFET parameters (e.g., electron mobility µn and SiO2 capa- citance Cox) factor into the modeling of lumped drain-source dynamic resistance and inverter switching speed. Hence, it’s here where the CpE/EE begins to understand the very real switching characteristics of a discrete transis- tor and particularly, switching time and power dissipation consequences. These distinctives [6] are in stark contrast with what students previously assumed to be a logic-function building block embedded in an integrated circuit.
If the CpE/EE student chooses to pursue more advanced courses in the areas of digital electronic circuits or digital logic operations, they have a variety of advanced-undergraduate courses to choose from [11] - [17] . Tradi- tionally, these courses are structured to teach 1) the analysis and design of CMOS integrated circuits; 2) archi- tectures and implementations of data converters; 3) energy-efficient VLSI design; 4) the development of hard- ware for embedded microcontroller systems. As practical as these courses are to the development of computing architectures, rigorous and abstract mathematical concepts relating to the explicit physical switching dynamics of digital circuits are not covered.
Hence, the CpE/EE intent on establishing a rigorous, mathematical description of switched electronic systems might consider courses in Switching Systems and Automata, Switching Theory and Logic Design, or just Switch- ing Theory. Texts examined on these topics tend to be presented from a rigorous, algebraic treatment [18] - [22] or from a CpE/EE or a computer science context with an introductory chapter on pure algebraic fundamentals [23] - [26] . Some exceptions are [27] - [29] . Those authors present a fairly rigorous mathematical treatment of Boo- lean operations and switching devices in early chapters, followed by classic and practical applications of the theory to the design of combinational and sequential architectures in later chapters.
Regardless of the presentation, the texts examined are traditionally presented to advanced graduate-level stu- dents in computer engineering, computer science, pure, or applied mathematics. It’s not characteristic for un- dergraduate CpE/EE’s to learn how to take pure or abstract mathematical concepts and conceptualize these ab- stractions into something tangible (e.g., a physical digital circuit). Consequently, undergraduate CpE/EE’s are not likely to cross-correlate Boolean switching abstractions with the physical properties of a transistor. The au- thor sees the benefit of such a unified exposure at a level that is appropriate for junior CpE/EE’s.
2. Conceptual Framework
Conceptual-abstract thinking consists of one’s ability to effectively find connections or patterns between abstract ideas. The subsequent task is to then piece ideas together to form a coherent picture [30] . The latter portion of this sentence “… piece ideas together to form a coherent picture” inherently involves other forms of thinking (e.g., analytical and inductive thinking). Thus, when presented with generalized non-physical mathematical con- cepts, how effectively would a traditional CpE/EE junior form a conceptual discernment of such abstractions in the context of familiar logic structures and transistor devices?
From a classical cognitive viewpoint [31] mental abstractions are represented by a set of defining features. For instance, how does a junior CpE/EE learn to differentiate between a MOSFET and a bipolar-junction tran- sistor (BJT)? From a black-box perspective (the abstract), both are three-terminal semiconductor devices and both can be biased to operate as a linear amplifier or as a digital switch (less abstract). In cognition research, men- tal perceptions of this type (e.g., digital switch) are referred to as structured representations. Without a com- prehensive understanding of specific defining features like 1) device physical operation; 2) device i-v characte- ristics, the MOSFET and BJT would remain pure abstractions.
The MOSFET has many very specific defining features such as enhancement of a current flow channel via the application of an electric field E, a threshold voltage Vt, an oxide capacitance Cox, and an aspect ratio W/L. These features are essential for describing the concept of “MOSFET” and distinguishing it as a unique three-terminal device. The feature of a new abstract stimulus [32] - [34] ―for instance, introduction to the BJT―is assessed by the student against the features of the concreteness of the MOSFET in order to determine if the BJT is an exam- ple of that category. When being introduced to the abstraction “BJT”, the student might ask a series of questions, for instance: “Does the BJT have a pn-structure similar to that of a MOSFET? Does the BJT operate on the same principle as the MOSFET? Are BJT i-v characteristics similar to those of a MOSFET? Can the BJT be biased to operate linearly like a MOSFET?”―and so forth. The student might conclude subsequently that the BJT can be made to function like a MOSFET in amplifying signals. However, students learn that the BJT doesn’t operate on the same principle as a MOSFET. Hence, the latter might come to be understood as a characteristic feature of a MOSFET but not necessarily a defining feature of a transistor. In other words, students come to understand the MOSFET is uniquely characteristic in its operation, but that it’s not necessary for a transistor to operate on this principle for it to function as a linear amplifier or a digital inverter.
What about a case where there are no defining features of a device abstraction but characteristic features only? For instance, a truth table might have the characteristic features of a three-input NAND gate. But in the absence of defining features, how can one make a concrete determination that it’s data from a 74LVC1G10 [35] ? It could very well be three discrete CMOS inverters being fed into a 74LVC1G332three input OR gate [36] . Hence, one can conclude that abstractions may either be represented by a set of features which are characteristic, or proba- ble of familiar examples [32] ―for instance, the truth table is probably that of a three-input NAND gate. This viewpoint can be extended to mathematical abstractions. For instance, mathematical abstractions are generally presented with precise definitions, corollaries, or lemmas.
3. Purpose
An exercise is proposed to promote the association of the physical characteristics of dynamic switching in a CMOS inverter with concepts taken from the abstract algebra. The objective is to present the CpE/EE junior with a basic algebraic abstraction and through a series of fundamental steps, engage the students’ abstract and inductive thinking into realizing the abstraction into the physical switching characteristics of a CMOS inverter. CMOS technology was chosen because inverter switching-speeds and steady-state response times approximate a hypothetical switch.
4. The Proposed Exercise
Consider the algebraic symbol x as being a number of the set S, such that x Î S. The task is to manipulate the symbol x of the set S using a binary operation.
DEFINITION I: A binary operation on a set S is a rule that associates with each ordered pair of elements in S a unique element of S. It’s a mapping which sends elements of the Cartesian product S ´ S → S. Because the re- sult of performing the operation on a pair of elements of S is again an element of S, the operation is called a closed binary operation on S.
DEFINITION II: Given an element x in S, if there exists and element y Î S such that x Ú y = 1 and x Ù y = 0, then y is called a complement of x.
From these definitions perform the following tasks:
a) Arrange the following objects into a representation of the operation f: S →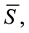 labeling which object is f. The arrows along with the other scattered shapes ought to be nicely arranged. Label the input(s) and output(s) using a variable of your choice.
labeling which object is f. The arrows along with the other scattered shapes ought to be nicely arranged. Label the input(s) and output(s) using a variable of your choice.

b) Construct a complete truth table for the operation in a.
c) Use the following Boolean theorems to prove complementation:
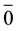 = 1;
= 1;
 = 0
= 0
Theorem 1: 0 Ù x = 0; 1 Ú x = 1
Theorem 2: x Ù (x Ú y) = x = x Ú (x Ù y)

As a CpE/EE major you’re aware that real-life electronic circuits can perform complementation (e.g., a TTL 7404 NOT gate). Likewise, you’re aware that TTL circuitry doesn’t act alone; the output of one logic gate ulti- mately feeds into the input of another. Consequently, there are parasitic capacitances that realistically affect the speed of the complementation operation. As a result of this capacitance, Vin is not complemented instantaneously but involves a propagation delay tp as illustrated in Figure 1. For instance, the operation
 = 0 involves the de- lay tpHL, where the subscript “pHL” represents the propagation time it takes a complementation circuit to switch (map) a 1 (HIGH) to a 0 (LOW).
= 0 involves the de- lay tpHL, where the subscript “pHL” represents the propagation time it takes a complementation circuit to switch (map) a 1 (HIGH) to a 0 (LOW).
Consider now the complementation model (Figure 2), representing one of two possible states of the CMOS inverter of Figure 1:
where RP(ON) is the drain-to-source resistance of QP during its on state, and C represents the lumped-loading parasitic capacitance.
Figure 1. CMOS inverter performing the Boolean operation
 = 1 and
= 1 and
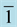 = 0 (where 1 = VDD). The time delays
= 0 (where 1 = VDD). The time delays
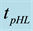 and
and
 brings about the notion that the switching is not instan- taneous.
brings about the notion that the switching is not instan- taneous.
Figure 2. One possibe state of Figure 1.

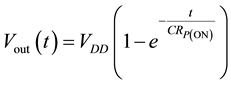
e) Discuss under what condition this seemingly continuous-time solution in d. approximates the Boolean ab- straction S→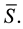

where Vt is the threshold voltage of transistor QP. Discuss in detail how hole mobility µp (cm2/V∙s) and the SiO2 capacitance Cox (Farads/meter2 or Amp-second/Volt∙meter2) affect the speed of complementation and therefore, how these two parameters limit the instantaneous complementation of the abstraction S →
5. Conclusions
An exercise has been proposed for the purpose of engaging students’ thinking into realizing an algebraic ab- straction into the physical switching characteristics of a basic CMOS inverter circuit. This exercise is meant to be used in a clinical setting with advanced-junior CpE/EE majors.
The intellectual merit of this exercise is that it promotes conceptual-abstract and deductive thinking in the CpE/EE junior via a non-traditional presentation of complementation, where mental abstractions that are nor- mally presented in a pure and theoretical manner are represented by a set of defining features congruent with a CpE/EE’s assumed knowledge level in microelectronics.
The broader impact is that of advancing the clinician’s understanding of how a small and unique group of un- dergraduates practice abstract and deductive thinking in the process of making familiar mental associations (i.e., structured representations) when presented with a pure mathematical abstraction. This work bridges cognitive theories of object concepts [6] , concept elaboration [9] [10] and [31] , abstract stimuli [33] , and sensorimotor re- enactment [7] [8] and [34] with upper-level computer and electrical engineering education.
The subsequent research ambitions of the author are to establish the validity and reliability of this exercise as an abstract reasoning assessment in a clinical setting. The objective is to dispense this exercise between the pre- and post-test administration of an established abstract and/or intelligence test battery, e.g., [37] - [40] .
References
- Razavi, B. (2008) Fundamentals of Microelectronics. John Wiley & Sons, New York.
- Neamen, D. (2008) Microelectronic Circuit Analysis and Design. McGraw-Hill, New York.
- Jaeger, R. and Blalock, T. (2010) Microelectronic Circuit Design. McGraw-Hill, New York.
- Sedra, A. and Smith, K. (2010) Microelectronic Circuits. Oxford University Press, New York, Oxford.
- IEEE Standard 1076-2008 (2009) VHDL Language Reference Manual. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4772740
- Martin, A. (2007) The Representation of Object Concepts in the Brain. Annual Review of Psychology, 58, 25-45. http://dx.doi.org/10.1146/annurev.psych.57.102904.190143
- Damasio, R. (1989) Time-Locked Multiregional Retro-Activation: A Systems Level Proposal for the Neural Substrates of Recall and Recognition. Cognition, 33, 25-62. http://dx.doi.org/10.1016/0010-0277(89)90005-X
- Simmons, K. and Barsalou, W. (2003) The Similarity-in-Topography Principle: Reconciling Theories of Conceptual Deficits and the Organization of Conceptual Knowledge in the Brain: Neuropsychological and Neuroimaging Perspec- tives. Cognitive Neuropsychology, 20, 451-486. http://dx.doi.org/10.1080/02643290342000032
- Barsalou, L. (1999) Perceptual Symbol Systems. Behavioral and Brain Sciences, 22, 577-609.
- Simon, A., Tzur, R., Heinz, K. and Kinzel, M. (2004) Explicating a Mechanism for Conceptual Learning: Elaborating the Construct of Reflective Abstraction. Journal for Research in Mathematics Education, 35, 305-329. http://dx.doi.org/10.2307/30034818
- Georgia Tech (2014) In 2014-2015 School of Electrical and Computer Engineering Projected Schedule of Graduate Courses. ECE Course Information. http://www.ece.gatech.edu/academics/graduate/course_schedule.pdf
- Oregon State University (2014) ECE Graduate Courses. In 2014-2015 General Catalog and Schedule of Classes. http://catalog.oregonstate.edu/CourseList.aspx?subjectcode=ECE&level=grad&campus=corvallis
- Penn State (2014) In 2014-2015 Department of Electrical Engineering, Graduate 500-Level Courses. http://www.ee.psu.edu/Undergraduate/CourseDescriptions.aspx#Grad500
- Purdue (2014) ECE Graduate Level Courses. In 2014-2015 Course Information: School of Electrical and Computer Engineering. https://engineering.purdue.edu/ECE/Academics/Undergraduates/UGO/CourseInfo/coursesGrad
- Stanford University (2014) Explore Courses. In 2014-2015 Stanford Bulletin. https://explorecourses.stanford.edu/search?q=EE&view=catalog&page=0&academicYear=&filter-term-Autumn=on&filter-term-Winter=on&filter-term-Spring=on&collapse=&filter-coursestatus-Active=on&filter-departmentcode-EE=on&filter-catalognumber-EE=on
- Texas A&M University (2014) In 2014-2015 Course Descriptions―Graduate Courses, Electrical & Computer Engineering. http://engineering.tamu.edu/electrical/academics/courses/descriptions#graduate
- University of Washington (2014) Course Descriptions. In 2014-2015 University of Washington Electrical Engineering. http://www.ee.washington.edu/academics/course_descriptions.html
- Lidl, R. and Pilz, G. (1998) Applied Abstract Algebra. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-2941-2
- Durbin, J. (2005) Modern Algebra: An Introduction. John Wiley & Sons, Hoboken.
- Roberts, F. and Tesman, B. (2008) Applied Combinatorics. CRC Press, Boca Raton.
- Even, G. and Medina, M. (2012) Digital Logic Design: A Rigorous Approach. Cambridge University Press, Cambridge, New York, Melbourne. http://dx.doi.org/10.1017/CBO9781139226455
- Judson, T. (2013) Abstract Algebra: Theory and Applications. Orthogonal Publishing, Ann Arbor.
- Rao, V. (1989) Switch-Level Timing Simulation of MOS VLSI Circuits. Kluwer Academic Publishers, Norwell.
- Fabricius, E. (1992) Modern Digital Design and Switching Theory. CRC Press, Boca Raton.
- Epstein, G. (1993) Multiple-Valued Logic Design. IOP Publishing, England.
- Kohavi, Z. and Jha, N. (2010) Switching and Finite Automata Theory. Cambridge University Press, Cambridge, New York, Melbourne.
- Hill, F. and Peterson, G. (1981) Introduction to Switching Theory & Logical. John Wiley & Sons, New York.
- Sasao, T. (1999) Switching Theory for Logic Synthesis. Kluwer Academic Publishers, Norwell. http://dx.doi.org/10.1007/978-1-4615-5139-3
- Astola, J. and Stankovic, R. (2006) Fundamentals of Switching Theory and Logic Design: A Hand on Approach. Springer, Berlin.
- Ojose, B. (2008) Applying Piaget’s Theory of Cognitive Development to Mathematics Instruction. The Mathematics Educator, 18, 26-30.
- Hershkowitz, R., Schwarz, B. and Dreyfus, T. (2001) Abstraction in Context: Epistemic Actions. Journal for Research in Mathematics Education, 32, 195-222. http://dx.doi.org/10.2307/749673
- Tervaniemi, M., Maury, S. and Näätänen, R. (1994) Neural Representations of Abstract Stimulus Features in the Hu- man Brain as Reflected by the Mismatch Negativity. Neuroreport, 5, 844-846. http://dx.doi.org/10.1097/00001756-199403000-00027
- McGuire, P., Paulesu, E., Frackowiak, R. and Frith, C.D. (1996) Brain Activity during Stimulus Independent Thought. Neuroreport, 7, 2095-2099.
- Kandel, E., Schwartz, J. and Jessell, T. (2000) Principles of Neural Science. McGraw-Hill Health Professions Division, Upper Saddle River, New York, San Francisco, London.
- NXP Semiconductor (2014) 74LVC1G10 Single 3-Input NAND Gate Product Data Sheet. http://www.nxp.com/documents/data_sheet/74LVC1G10.pdf
- NXP Semiconductor (2014) 74LVC1G332 Single 3-Input OR Gate Product Data Sheet. http://www.nxp.com/documents/data_sheet/74LVC1G10.pdf
- Wechsler, D. (1958) The Measurement and Appraisal of Adult Intelligence. The Williams & Wilkins Company, Baltimore. http://dx.doi.org/10.1037/11167-000
- Wechsler, D. (2008) Wechsler Adult Intelligence Scale, Fourth Edition (WAIS-IV). Pearson PsychCorp., San Antonio.
- ACER (2014) Test of Abstract Reasoning Manual. https://www.psychometrics.com/docs/tar-manual.pdf
- Australian Council for Educational Research (ACER) (2014) Clinical Assessments. http://www.acer.edu.au/assessment/all-clinical-assessments






