World Journal of Engineering and Technology
Vol.02 No.03(2014), Article ID:48696,10 pages
10.4236/wjet.2014.23023
Implicit and Explicit Analysis of the Response of Blast Loaded Reinforced Concrete Slabs
Kamel S. Kandil1, Mouhamad T. Nemir1, Ehab A. Ellobody2, Ramy I. Shahin1*
1Department of Civil Engineering, Faculty of Engineering, Menoufiya University, Shibin El Kom, Egypt
2Department of Structural Engineering, Faculty of Engineering, Tanta University, Tanta, Egypt
Email: *Ramy.Shahin@Gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2014; revised 21 July 2014; accepted 3 August 2014
ABSTRACT
Implicit and explicit analyses were examined with experimental work done by Razaqpur et al. In the experiment work, two 1000 × 1000 × 70 mm reinforced concrete slabs were constructed. The slabs were subjected to blast loads generated by the detonation of either 22.4 kg or 33.4 kg of ANFO located at a 3.0 m standoff. Blast wave characteristics, including incident and reflected pressures and reflected impulses were measured. The slabs were modeled by implicit and explicit analysis to study their behavior under blast load to compare their predicted and observed behavior. The post-blast damage and mode of failure of each slab were observed. It was concluded that explicit analysis provides better modeling than implicit analysis.
Keywords:
Implicit Analysis, Explicit Analysis, Strain Rate, Blast Load, Ansys, Ls-Dyna, Scaled Distance

1. Introduction
Since testing of structures under the effect of real explosives requires complex instrumentation and a safe test range, it is not always feasible to carry out a large number of such tests. Therefore, to gain deeper insight into the detailed behavior and performance of structures under blast loads, one must resort to analytical and advanced numerical techniques. However, the results of the analysis must be confirmed by some amount of testing to ensure the validity of the assumptions and procedures used in the analysis.
The basic equation of motion solved by a transient dynamic analysis is:
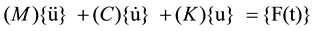 (1)
(1)
where
(M) = mass matrix
(C) = damping matrix
(K) = stiffness matrix
{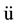 } = nodal acceleration vector
} = nodal acceleration vector
{ } = nodal velocity vector
} = nodal velocity vector
{u} = nodal displacement vector
{F(t)} = load vector
There are two methods which can be employed for the solution of Equation (1): the forward difference time integration method and the Newmark time integration method. The Newmark method is used for implicit transient analyses by ANSYS program. The forward difference method is used for explicit transient analyses by Ls-Dyna program.
Implicit FEM analysis does the incremental procedure and after each increment, the analysis does Newton- Raphson iterations to enforce equilibrium of the internal structure forces with the externally applied loads. At the end of each increment, the stiffness matrix based on geometry changes and material changes (if applicable) is updated. The equilibrium is usually enforced to some user specified tolerance.
Explicit FEM analysis applies incremental procedure for load (or displacement), and at the end of each increment, it updates the stiffness matrix based on geometry changes and material changes (if applicable). Then a new stiffness matrix is constructed, and the next increment of load (or displacement) is applied to the system. This method does not enforce equilibrium of the internal structure forces with the externally applied loads. Therefore, the hope is that if the increments are small enough, the results will be accurate.
The forward difference time integration method and the Newmark time integration method can be used to simulate structures under blast load. Researchers use one of these methods in modeling. But it is not clear which method provides better presentation for blast load. Blast load is an example of impulsive loading where loading is applied in a very short duration.
The first objective of this paper is to propose two models to simulate reinforced concrete panels under blast load: the first model is based on implicit analysis by ANSYS program and the second model is based on explicit analysis by Ls-Dyna program. The second objective is to compare the observed behavior of reinforced concrete panels, subjected to nominally similar blast loads, namely maximum central deflection and observed damage in test slabs, with their predicted behavior using ANSYS for implicit analysis and Ls-Dyna for explicit analysis. This comparison helps to find out the best simulation method for reinforced concrete elements under blast load.
2. Experimental Work
Seven 1000 × 1000 × 70 mm reinforced concrete slabs (Figure 1) were identically doubly reinforced with welded steel mesh of bar cross-sectional area of 25.8 mm2, and center-to-center spacing of 152 mm in each direction, mass per unit area of 2.91 kg/m2, yield stress of 480 MPa and ultimate strength of 600 MPa. The concrete had an average 28 day compressive strength of 40 MPa [1] .
The slabs designated CS2 to CS4 were as-built while other panels were retrofitted on each face with two sheets of GFRP [1] . This study focused on as-built panels.
The free field incident pressure was measured by at least two transducers located, at 3.2 and 5.9 m from the center of each test slab. Reflected pressure was measured 3.1 m from the charge center by four transducers located at the mid-length of the four sides of the slab. An LVDT was used to measure the slab central displacement [1] .
To commence the test, the tripod holding the charge was centered above the center of the panel and the charge was hung with a wire. The distance from the center of the charge to the center of the test panel was 3.0 m for all panels. The explosive used was ANFO, comprising 5.7% fuel oil and 94.3% ammonium nitrate, shaped into an approximately spherical form. The explosive energy of ANFO is 3717 kJ/kg, which is 82% of the energy of one kilogram of TNT [1] . Figure 2 shows a test specimen in place and the tripod holding the charge.
It should be noted that specimen CS4 was subjected to the pressure produced by a 22.4 kg charge while the remaining specimens were exposed to the load caused by the detonation of a 33.4 kg charge. In this study, the results of specimens CS2 and CS3 are considered in the comparison with their counterpart of the predicted
Figure 1. Test specimen geometry and reinforcement details. (All dimensions in mm).
Figure 2. Test specimen with the tripod holding the explosive charge.
explicit analysis, as the post-blast observed damage in the un-retrofitted test panels was available for CS2 and CS3.
In both models, the slab support was assumed to be hinged.
3. Implicit Analysis
In this model, the time history curve based on TM5-1300 [2] was used in conjunction with SOLID65 element in ANSYS program. The time history curve was based on Chengqing Wu and Hong Hao [3] [4] empirical attenuation relations which is based on TM5-1300 [2] .
The reflected pressure generated by the detonation of 33.4 kg of ANFO and 3.0 m distance from the center of the charge to the center of the test panel was equal to 4.94 MPa according to TM5-1300 [1] [2] . The time history curve for reflected pressure in the positive phase is shown in Figure 3.
The most important aspect of SOLID65 element is the treatment of nonlinear material properties. Multilinear isotropic material was used for concrete. Stress strain curve is shown in Figure 4 [5] .
Multilinear isotropic material is capable of cracking (in three orthogonal directions), crushing, plastic deformation, and creep. The two input strength parameters―i.e., ultimate uniaxial tensile and compressive strengths? are needed to define a failure surface for the concrete. After cracking, the elastic modulus of the concrete element is set to zero in the direction parallel to the principal tensile stress direction. 3D model is shown in Figure 5. Crushing occurs when all principal stresses are compressive and lie outside the failure surface; subsequently, the elastic modulus is set to zero in all directions [6] [7] .
The rebar are capable of tension and compression, but not shear. They are also capable of plastic deformation [6] . Reinforcement representation in this model was smeared reinforcement in solid elements. Rebar properties are input as real constants, The material number is chosen for rebar Material, the volume ratio is estimated, and the orientation angles is taken 0 and 90 in the x-y plane to represent the reinforcement in X and Y directions.
The finite element slab models fail prematurely. Crushing of the concrete started to develop in elements located directly under the loads. Subsequently, adjacent concrete elements crushed within several load steps as well, significantly reducing the local stiffness.
Finally, the model showed a large displacement, and the solution diverged. So, in nonlinear analysis, the total load applied to a finite element model is divided into a series of load increments called load steps. At the completion of each incremental solution, the stiffness matrix of the model is adjusted to reflect nonlinear changes in structural stiffness before proceeding to the next load increment using Newton-Raphson equilibrium iterations for updating the model stiffness. The static load is added as steps until the plate reach the total failure where the
Figure 3. Time history curve for reflected pressure in the positive phase.
Figure 4. Stress-strain curve for concrete material.
Figure 5. 3D model by ANSYS program.
analysis is terminated due to convergence problems. The latest converged step is used to read the results just before total failure. Maximum displacement was at the center of plate, and it was equal to 36.5 mm as shown in Figure 6. The analytical displacement is larger than maximum measured central displacement, and this may refer to the strain rate effect. When the loading rate is high, the mechanical response of a material is generally different from that at a low loading rate.
Typically, all damaged panels had full depth inverted 45˚ shear cracks near their supports and on all four sides. These cracks were rather wide and in some cases greater than 4 mm [1] .
Experimentally, it was also observed on the bottom surface of most panels an array of 500 mm long cracks formed a square shape centered on the panel center and propagated diagonally towards the corners of the panel, also cracks inside the square were noted (see Figure 17(a)). This is agreeing with the combination of first plane cracks and second phase cracks in Figure 7 and Figure 8, respectively.
These cracks are similar to the yield line pattern for a statically applied central patch load.
On the bottom surface, additional minor cracks, which typically followed the reinforcement layout, were also observed in experimental and analytical model where in plane cracks were observed, which means that the bond between concrete and steel are demolished.
On the compression face, the cracks do not extend to the center of plate. In addition, some cracks are propagated perpendicular to the diagonal cracks, which is also assigned in the 1st and 2nd phase cracks shown in Figure 9. However, observed diagonal cracks in the plates extend to the center of plate more than analytical results (see Figure 16(a)). This may refer to the fact that the analytical work does not solve the model to the full load step. It is possible to note that the cracks happened in several phases that indicate total failure for the plate. This agrees with experimental results. This is also explaining why the solution is not complete to the maximum pressure value.
4. Explicit Analysis
In Ls-Dyna Program, Piecewise Linear Isotropic Plasticity material is used. This material includes strain rate effects [8] . Concrete exhibits an enigmatic phenomenon of increased resistance when it is loaded at a very high rate [9] [10] . To account for strain rate, the stress strain curve for static strain rate “equal to 3.0E−05” is plotted [5] . Then, the Dynamic Increase Factor (DIF), i.e. the ratio of the dynamic to static strength, is calculated using CEB formula for compression [11] - [13] . Erosion is added as a way of including failure in these models. In this model, the concrete material fails under principal strain for concrete material. See Figure 10 for stress strain curve for concrete material under different strain rates.
Elastic plastic with kinematic hardening material is used for reinforcement bars (see Figure 11). Strain rate is accounted for using the Cowper and Symonds [8] model which scales the yield stress by a strain rate dependent factor. See Figure 12 for the meshing of concrete panel.
Figure 6. Displacement contour at last converged step.
Figure 7. Cracking & crushing at tension plane “first crack phase”.
Figure 8. Cracking & crushing at tension plane “second crack phase”.
Figure 9. Cracking & crushing at compression face.
Figure 10. Stress-strain curve for piecewise linear isotropic plasticity concrete material under different strain rates.
Blast loading was calculated using the empirical blast loading functions implemented in the CONWEP code based on TM5-1300 technical manual [2] . Free air detonation of 33.4 kg spherical charge was used. In Ls-Dyna program, this function is available in Blast Load Command [8] .
Experimentally, it was observed on the bottom surface of most panels an array of 500 mm long cracks formed a square shape centered on the panel center and propagated diagonally towards the corners of the panel. Also, cracks inside the square were noted. These cracks are similar to the yield line pattern for a statically applied central patch load. On the bottom surface, additional minor cracks, which typically followed the reinforcement layout, were also observed in experimental model.
Analytically, in the bottom “tension” face, cracks are propagates in center and extend to the edges in the same time (see Figure 13(b)). Then, cracks size increased particularly at center and corners of panel (see Figure 13(c) and Figure 13(d)).
In the top “compression” face, diagonal cracks are propagates (see Figure 14(b)). The size and location of cracks remain unchanged at the end of blast load (see Figure 14(c) and Figure 14(d)).
In Ls-Dyna model, the size of square shape array is 550 mm long and the damage in yield line region extend to the 50% of the plate thickness. Addition damages are also noted at support boundary (see Figure 13 and Figure 14).
The maximum experimental central deflection for the two identical plates was 13.12 mm for panel CS2 and 9.53 mm for panel CS3, with an average deflection of 11.33 mm. Maximum central deflection in explicit Ls- Dyna model was 11.66 mm as seen in Figure 15 which agree very well with experimental work.
Damage pattern in Ls-Dyna model is more close to experimental work as seen in Figure 16 and Figure 17.
This means that the material behavior under high strain rates play an important role in the analytical work.
Figure 11. Front view for in the Ls-Dyna model showing reinforcement bar.
Figure 12. Plan for the Ls-Dyna model showing meshing for experiment.
Figure 13. Cracking & crushing propagation at tension face of Ls- Dyna model.
Figure 14. Cracking & crushing propagation at compression face of Ls-Dyna model.
Figure 15. Central time-displacement curve for Ls-Dyna model in (m).

Figure 16. Predicted Ls-Dyna model and field observed damage in a typical test slab [top face]. (a) Observed damage; (b) Predicted damage.

Figure 17. Predicted Ls-Dyna model and field observed damage in a typical test slab [bottom face]. (a) Observed damage; (b) Predicted damage.
5. Conclusions
The comparison between the field test results for the slabs subjected to a 33.4 kg shot was compared well with the results of the explicit analysis using Ls-Dyna. Explicit analysis using Ls-Dyna model provides much better presentation than implicit analysis using ANSYS model for the following reasons:
1. In implicit analysis, analysis is terminated due to convergence problems before reaching the peak blast reflected pressure. In explicit analysis, the analysis continues to the end of blast load.
2. The maximum deflection at the center of plate for explicit analysis is much closer to experiment measurements than implicit analysis.
3. Predicted damage patterns in Ls-Dyna model are closer to experimental work than ANSYS model.
In addition, strain rate effect is vital to get good presentation for blast load. It is important to account for dynamic increase factor for concrete and steel material for high strain rate loads such as blast and impact.
References
- Ghani Razaqpur, A., Tolba, A. and Contestabile, E. (2007) Blast Loading Response of Reinforced Concrete Panels Reinforced with Externally Bonded GFRP Laminates. Elsevier Journal of the Composites: Part B, 38, 535-546. http://dx.doi.org/10.1016/j.compositesb.2006.06.016
- TM-5-1300 (1990) Design of Structures to Resist the Effects of Accidental Explosions. Technical Manual, US Department of the Army, Washington DC.
- Wu, C.Q. and Hao, H. (2005) Modeling of simultaneous Ground Shock and Airblast Pressure on Nearby Structures from Surface Explosions. Elsevier International Journal of Impact Engineering, 31, 699-717. http://dx.doi.org/10.1016/j.ijimpeng.2004.03.002
- Wua, C.Q. and Hao, H. (2007) Numerical Simulation of Structural Response and Damage to Simultaneous Ground Shock and Airblast Loads. Elsevier International Journal of Impact Engineering, 34, 556-572. http://dx.doi.org/10.1016/j.ijimpeng.2005.11.003
- Ellobody, E. and Bailey, C.G. (2008) Behaviour of Unbonded Post-Tensioned One-Way Concrete Slabs. Reprinted from Advances in Structural Engineering, 11, 117-120.
- ANSYS, ANSYS User’s Manual, Version 11.0, ANSYS, Inc.
- Kachlakev, D. and Miller, T. (2001) Finite Element Modeling of Reinforced Concrete Structures Strengthened With FRP Laminates. SPR 316, Oregon Department of Transportation Research Group & Federal Highway Administration, Washington DC.
- Livermore Software Technology Corporation (2003) Ls-Dyna Theoretical Manual. Livermore Software Technology Corporation, California.
- Faust, B. (2002) Evaluation of the Residual Load-Bearing Capacity of Civil Structures Using Fuzzy-Logic & Decision Analysis. Universität Der Bundeswehr, Neubiberg.
- Lu, Y. and Xu, K. (2004) Modeling of Dynamic Behaviour of Concrete Materials under Blast Loading. International Journal of Solids and Structures, 41, 131-143. http://dx.doi.org/10.1016/j.ijsolstr.2003.09.019
- Javier Malvar, L. and Crawford, J.E. (1998) Dynamic Increase Factors for Concrete. Twenty-Eighth DDESB Seminar, Orlando, August 1998.
- Moon, N. (2009) Prediction of Blast Loading and Its Impact on Buildings. Master of Technology in Civil Engineering Thesis, Department of Civil Engineering, National Institute of Technology, Rourkela.
- Ngo, T., Mendis, P., Gupta, A. and Ramsay, J. (2007) Blast Loading and Blast Effects on Structures―An Overview. Electronic Journal of Structural Engineering, EJSE Special Issue: Loading on Structures, 76-91.
NOTES
*Corresponding author.



















