Advances in Materials Physics and Chemistry
Vol.07 No.05(2017), Article ID:76286,11 pages
10.4236/ampc.2017.75017
Metal-Insulator Transition of Peierls Type in Quasi-One-Dimensional Crystals of TTT2I3
Silvia Andronic, Anatolie Casian
Department of Computers, Informatics and Microelectronics, Technical University of Moldova, Chisinau, Moldova

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 31, 2017; Accepted: May 19, 2017; Published: May 22, 2017
ABSTRACT
We investigate the metal-insulator transition in quasi-one-dimensional organic crystals of tetrathiotetracene-iodide, TTT2I3, in the 2D model. A crystal physical model is applied which takes into account two the most important hole-phonon interaction mechanisms. One is similar to that of deformation potential and the other is of polaron type. The scattering on defects is also considered and it is crucial for the explanation of the transition. The phonon polarization operator and the renormalized phonon spectrum are calculated in the random phase approximation for different temperatures applying the method of Green functions. We show that the transition is of Peierls type. The effect of lattice distortion on the dispersion of renormalized acoustic phonons is analyzed.
Keywords:
Quasi-One-Dimensional Organic Crystals, TTT2I3, Polarization Operator, Metal-Insulator Transition, Peierls Transition, Interchain Interaction, Renormalized Phonons

1. Introduction
Quasi-one-dimensional (Q1D) organic crystals of tetrathiotetracene-iodide, TTT2I3, were synthesized independently and nearly simultaneously [1] [2] [3] [4] with the aim to find superconductivity in a low dimensional conductor. However, these crystals with rather high electrical conductivity near room temperature, at low temperature showed a transition into a dielectric state. Such transition has firstly observed in the Q1D charge transfer compound TTF-TCNQ (tetrathiafulvalene-tetracyanoquinodimethane) [5] [6] and was the first experimental confirmation of the structural transition, predicted earlier by Peierls [7] in 1D conductors.
TTT2I3 is also a charge transfer compound. The orthorhombic crystal structure consists of segregated chains or stacks of plane TTT molecules and of iodine chains. The lattice constants are a = 18.40 Å, b = 4.96 Å and c =18.32 Å, which demonstrates a very pronounced crystal quasi-one-dimensionality. The highly conducting direction is along b. The compound is of mixed valence. Two molecules of TTT give one electron to iodine chain formed of 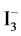 ions that play the role of acceptors. Only TTT chains are conductive and the carriers are holes. The electrons on iodine ions are in a rather localized states and do not participate in the transport. In the crystals grown by sublimation of TTT and iodine in an inert gas flow [3] the room electrical conductivity σ along b direction achieves (103 - 104) Ω−1∙cm−1, but in those grown from solution [1] [2] σ ~ (800 - 103) Ω−1∙cm−1. Such variation in σ of crystals, grown in different laboratories, shows that the conductivity properties of TTT stacks are highly sensitive to defects and impurities. It is caused by the purity of initial materials and the conditions of crystal growth. In all crystals, with the lowering of temperature the conductivity firstly grows, reaches a maximum after that falls. The temperature of the maximum, Tmax, and the value of the ratio σmax/σ300 depends on the iodine content. Crystals with a surplus of iodine, TTT2I3.1, have Tmax ~ (34 - 35) K and very sharp fall of σ(T) after the maximum.
ions that play the role of acceptors. Only TTT chains are conductive and the carriers are holes. The electrons on iodine ions are in a rather localized states and do not participate in the transport. In the crystals grown by sublimation of TTT and iodine in an inert gas flow [3] the room electrical conductivity σ along b direction achieves (103 - 104) Ω−1∙cm−1, but in those grown from solution [1] [2] σ ~ (800 - 103) Ω−1∙cm−1. Such variation in σ of crystals, grown in different laboratories, shows that the conductivity properties of TTT stacks are highly sensitive to defects and impurities. It is caused by the purity of initial materials and the conditions of crystal growth. In all crystals, with the lowering of temperature the conductivity firstly grows, reaches a maximum after that falls. The temperature of the maximum, Tmax, and the value of the ratio σmax/σ300 depends on the iodine content. Crystals with a surplus of iodine, TTT2I3.1, have Tmax ~ (34 - 35) K and very sharp fall of σ(T) after the maximum.
The aim of present paper is to demonstrate that this sharp decrease of σ(T) is determined by the Peierls structural transition in the TTT chains. At our knowledge, the Peierls transition in TTT2I3 was not studied neither theoretically, nor experimentally. It is known that the Peierls structural transition is connected by the competition of two processes that take place, when the temperature is decreased. From one side, it is favorable that the lattice distorts because this diminishes the electronic energy of the crystal, lowering the Fermi energy. However, this distortion increases the lattice elastic energy. At some temperature, named the Peierls critical temperature Tp, when the first process prevails over the second one, a Peierls structural transition takes place.
The Peierls structural transition has been studied in many Q1D crystals [8] - [14] . In TTF-TCNQ crystals, the transition takes place at 54 K into TCNQ stacks and at 38 K into TTF stacks with the opening of respective band gaps in the electronic spectrum above the Fermi energy and a strong diminution of electrical conductivity. We have also studied the transition at 54 K in a more complete physical model [15] [16] . With the lowering temperature, some modifications in the phonon spectrum take place [17] [18] , and at some temperature, the renormalized phonon frequency becomes equal to zero for a given value of the phonon wave vector. At this temperature the Peierls transition occurs.
Note that earlier the crystals of TTT2I3 have been investigated as good candidates for thermoelectric applications [19] [20] . It was predicted [21] [22] that after optimization of the carrier concentration in such crystals values of dimensionless thermoelectric figure of merit~4 could be realized. However, not all parameters of these crystals are determined experimentally. Other aim of present paper is to use the investigation of the Peierls transition in order to determine more precisely some parameters of TTT2I3.
We will apply a more complete crystal model [23] [24] , which takes into account two the most important hole-phonon interactions. The first interaction is similar to that of deformation potential and is determined by the variation of the transfer energy of a carrier from one molecule to the nearest one, caused by acoustic lattice vibrations. Other interaction is of polaron type and is determined by the variation of the polarization energy of molecules surrounding the conduction electron caused by the same acoustic vibrations. The scattering on structural defects is also taken into account. We show that the Peierls structural transition explains the sharp decrease of electrical conductivity in TTT2I3 at low temperature. The dispersion of renormalized phonons and the Peierls critical temperature are determined. For the simplicity, we consider the 2D physical model.
2. The Physical Model
We apply the two-dimensional physical model described in [16] for TTF-TCNQ crystals, considering the interchain interaction in the plane of TTT stacks small. The Hamiltonian of the crystal in the tight binding and nearest neighbor approximations has the form:
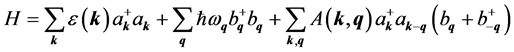 (1)
(1)
where the first term is the energy operator of free holes in the periodic field of the lattice, 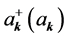 are the creation and annihilation operators of such hole with a two-dimensional wave vector k and projections (kx, ky). The energy of the hole
are the creation and annihilation operators of such hole with a two-dimensional wave vector k and projections (kx, ky). The energy of the hole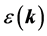 , measured from the top of conduction band, has the form:
, measured from the top of conduction band, has the form:
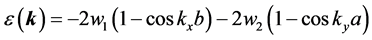 (2)
(2)
Here 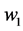 and
and 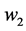 are the transfer energies of a hole from one molecule to another along the chain (x direction) and in perpendicular direction (y direction). In Equation (1)
are the transfer energies of a hole from one molecule to another along the chain (x direction) and in perpendicular direction (y direction). In Equation (1) 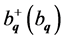 are creation and annihilation operators of an acoustic phonon with two-dimensional wave vector q and frequency
are creation and annihilation operators of an acoustic phonon with two-dimensional wave vector q and frequency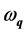 . The second term in the Equation (1) is the energy operator of longitudinal acoustic phonons,
. The second term in the Equation (1) is the energy operator of longitudinal acoustic phonons,
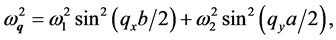 (3)
(3)
where 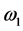 and
and 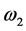 are limit frequencies for oscillations in x and y directions. The third term in Equation (1) represents the hole-phonon interactions. As it was mentioned above, two interaction mechanisms are considered: the first is similar to that of deformation potential and the second is of polaron type. The coupling constants of the first interaction are proportional to the derivatives
are limit frequencies for oscillations in x and y directions. The third term in Equation (1) represents the hole-phonon interactions. As it was mentioned above, two interaction mechanisms are considered: the first is similar to that of deformation potential and the second is of polaron type. The coupling constants of the first interaction are proportional to the derivatives 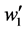 and
and 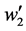 of
of 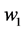 and
and 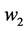 with respect to the intermolecular distances. The coupling constant of second interaction is proportional to the average polarizability of the molecule
with respect to the intermolecular distances. The coupling constant of second interaction is proportional to the average polarizability of the molecule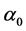 . This interaction is important for crystals composed of large molecules as TTT, so as
. This interaction is important for crystals composed of large molecules as TTT, so as 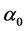 is roughly proportional to the volume of molecule.
is roughly proportional to the volume of molecule.
The square module of matrix element 

where M is the mass of the TTT molecule, N is the number of molecules in the basic region of the crystal, 


The analysis shows that the Hamiltonian from the Equation (1) can not explain the sharp decrease of electrical conductivity for temperatures lower than Tmax = 35 K, even, when we vary the crystal parameters and consider only the first interaction mechanism. It is necessary to take into account also the dynamical interaction of carriers with the defects. The static interaction will give contribution to the renormalization of hole spectrum. The defects in TTT2I3 crystals are created due to different coefficients of dilatation of TTT and iodine chains. The Hamiltonian of this interaction 

Here 


the derivative with respect to intermolecular distance from the energy of interaction of a carrier with a defect, 
where the constant D = 1.05 and determines the intensity of hole interaction with a defect.
In order to investigate the Peierls transition, the method of temperature dependent retarded Green functions is applied [25] . The retarded Green functions
for lattice displacements 

where 






The equation of motion for the operator uq is deduced as follows:

On the base of Equation (8), one can obtain the first equation for the Green function

Further, one can obtain the equation of motion for the new Green function

tions. In order to cut up the chain, let’s consider that the hole-phonon interaction is weak and express the three-particle Green function through the one-par- ticle Green function as follows

Thus, a closed equation for the function 
Now it is conveniently to pass to Fourier transformation of the function 


As a result, it follows:

where

From Equations (12) and (13) it results the expression for the Fourier transformation of the lattice displacement Green function

In order to distinguish the retarded Green function it is needed to put, 

aginary part of the renormalized lattice frequency.

The real part of Equation (15) will determine the renormalized lattice frequency Ω(q), as the solution of the transcendent equation

where the principal value of the dimensionless polarization operator takes the form:

Here, 

trix elements of the hole-phonon interaction from Equation (4), and of hole interaction with defects from Equation (6), the 
3. Results and Discussions
Computer simulations are performed for the following parameters [20] : M = 6.5 ´ 105 me (me is the mass of the free electron), w1 = 0.16 eV, 
Figures 1-4 present the dependences of renormalized phonon frequencies Ω(qx) as functions of qx for different temperatures and different values of qy . In the same graphs, the dependences for initial phonon frequency ω(qx) are presented too. It is seen that the values of Ω(qx) are diminished in comparison with those of frequency ω(qx) in the absence of hole-phonon interaction. This means that the hole-phonon interaction and structural defects diminish the values of lattice elastic constants. Also, one can observe that with a decrease of temperature T the curves change their form, and in dependencies Ω(qx) a minimum appears. This minimum becomes more pronounced at lower temperatures.
Figure 1 shows the case, when qy = 0. In this case the interaction between TTT chains is neglected. The Peierls transition begins at T = 35 K. At this temperature, the electrical conductivity is strongly diminished, so as a gap in the carrier spectrum is fully opened just above the Fermi energy. In addition, it is
Figure 1. Renormalized phonon spectrum Ω(qx) for γ1 = 1.7 and different temperatures. The dashed line is for the spectrum of free phonons. In this case qy = 0.
Figure 2. Renormalized phonon spectrum Ω(qx) for γ1 = 1.7 and different temperatures. The dashed line is for the spectrum of free phonons. The case of qy = π/4.
Figure 3. Renormalized phonon spectrum Ω(qx) for γ1 = 1.7 and different temperatures. The dashed line is for the spectrum of free phonons. The case of qy = 2kF.
Figure 4. Renormalized phonon spectrum Ω(qx) for γ1 = 1.7 and different temperatures. The dashed line is for the spectrum of free phonons. The case of qy = π.
seen that the slope of Ω(qx) at small qx is diminished in comparison with that of ω(qx). This means that the hole-phonon interaction and structural defects have reduced also the sound velocity in a large temperature interval. When the interaction between transversal chains is taken into account (qy ≠ 0), the temperature when Ω(qx) = 0 is diminished.
Figure 2 shows Ω(qx) for qy = π/4 and different temperatures. One can see that Ω(qx) attains zero at T ~ 30 K. Figures 2-4 correspond to the 2D physical model, qy ≠ 0.
When qy = 2kF (Figure 3), the temperature, when Ω(qx) = 0, decreases additionally and has the value of T = 21 K.
Figure 4 shows the dependences of Ω(qx) on qx for qy = π and different temperatures. It is observed that the temperature, when Ω(qx) = 0, decreases still more and equals T = 19 K, thus, our calculations show that at this temperature the Peierls transition is finished. A new superstructure must appear. Unfortunately, at our knowledge, such experiments were not realized. It would be interesting to verify experimentally our conclusions. As it is seen from [3] , at T = 19 K, the electrical conductivity is strongly reduced, but achieves zero at T = 10 K. This can be explained by further increase of the gap above the Fermi level, when the temperature decreases from 19 K to 10 K. The existence of an energy gap above the Fermi energy at temperatures higher than that of phase transition have been observed in crystals of tetramethyl tetrathiafulvalene [26] , which have similar to TTT2I3 temperature dependence of electrical conductivity.
Figure 5 and Figure 6 show the dependencies of the real part of dimensionless polarization operator 
In Figure 6 it is presented the same dependence of polarization operator as function of qx, but for qy = π. From this graph it is observed that, when the interaction between TTT chains is taken into account, the Peierls critical temperature decreases and transition is finished at T = 19 K.
4. Conclusion
We have investigated the behavior of phonons near Peierls structural transition in quasi-one-dimensional organic crystals of TTT2I3 (tetrathiotetracene iodide)
Figure 5. Polarization operator as function of qx for qy = 0 and T = 35 K.
Figure 6. Polarization operator as function of qx for qy = π and T = 19 K.
type in 2D approximation. A more complete crystal model is applied which takes into account two the most important hole-phonon interactions. One interaction is of deformation potential type and the other is similar to that of polaron. The ratios of amplitudes of second hole-phonon interaction to the first one along chains and in transversal direction are noted by γ1 and γ2, respectively. The interaction of holes with the structural defects in direction of TTT chains is taken into account too. Analytical expression for the polarization operator was obtained in random phase approximation. The method of retarded temperature dependent Green function is applied. The numerical calculations for renormalized phonon spectrum, Ω(qx), for different temperatures are presented in two cases: 1) when qy = 0 and the interaction between transversal chains is neglected and 2) when qy ≠ 0 and interactions between the adjacent chains are considered. It has been established that Peierls transition begins at T ~ 35 K in TTT chains and reduces considerably the electrical conductivity. Due to interchain interaction the transition is finished at T ~ 19 K. It is demonstrated that the hole-phonon interaction and the interactions with the structural defects diminish Ω(qx) and reduce the sound velocity in a large temperature interval.
Cite this paper
Andronic, S. and Casian, A. (2017) Metal-Insulator Transition of Peierls Type in Quasi-One-Dimen- sional Crystals of TTT2I3. Advances in Ma- terials Physics and Chemistry, 7, 212-222. https://doi.org/10.4236/ampc.2017.75017
References
- 1. Buravov, I.I., Zvereva, G.I., Kaminskii, V.F., et al. (1976) New Organic “Metals”: Naphthaceno[5,6-cd:11,12-c’d’]bis[1,2]dithiolium Iodides. Journal of the Chemical Society, Chemical Communications, No. 18, 720-721.
https://doi.org/10.1039/c39760000720 - 2. Kaminskii, V.F., Khidekel, M.L., Lyubovskii, R.B., et al. (1977) Metal-Insulator Phase Transition in TTT2I3 Affected by Iodine Concentration. Physica Status Solidi A, 44, 77-82.
https://doi.org/10.1002/pssa.2210440107 - 3. Hilti, B. and Mayer, C.W. (1978) Electrical Properties of the Organic Metallic Compound Bis(Tetrathiotetracene)-Triiodide, (TTT)2-I3. Helvetica Chimica Acta, 61, 501-511.
https://doi.org/10.1002/hlca.19780610143 - 4. Isset, L.G. and Perz-Albuerene, E.A. (1977) Low Temperature Metallic Conductivity in Bis(Tetrathiotetracene) Triiodide, a New Organic Metal. Solid State Communications, 21, 433-435.
- 5. Ferraris, J., Cowan, D.O., Walatka, W. and Perlstein, J.H. (1973) Electron Transfer in a New Highly Conducting Donor-Acceptor Complex. Journal of the American Chemical Society, 95, 948-949.
https://doi.org/10.1021/ja00784a066 - 6. Coleman, L.B., Cohen, M.J., Sandman, D.J., Yamagishi, F.G., Garito, A.F. and Heeger, A.J. (1973) Superconducting Fluctuations and the Peierls Instability in an Organic Solid. Solid State Communications, 12, 1125-1132.
- 7. Peierls, R. (1955) Quantum Theory of Solids. Oxford University Press, London.
- 8. Jerome, D. (2004) Organic Conductors: From Charge Density Wave TTF-TCNQ to Superconducting (TMTSF)2PF6. Chemical Reviews, 104, 5565-5592.
https://doi.org/10.1021/cr030652g - 9. Jerome, D. (2012) Organic Superconductors: When Correlations and Magnetism Walk in. Journal of Superconductivity and Novel Magnetism, 25, 633-655.
- 10. Pouget, J.P. (2012) Bond and Charge Ordering in Low-Dimensional Organic Conductors. Physica B: Condensed Matter, 407, 1762-1770.
- 11. Pouget, J.P. (2016) The Peierls Instability and Charge Density Wave in One-Dimensional Electronic Conductors. Comptes Rendus Physique, 17, 332-356.
https://doi.org/10.1016/j.crhy.2015.11.008 - 12. Streltsov, S.V. and Khomskii, D.I. (2014) Orbital-Dependent Singlet Dimers and Orbital-Selective Peierls Transitions in Transition-Metal Compounds. Physical Review B, 89, Article ID: 161112.
https://doi.org/10.1103/physrevb.89.161112 - 13. Chernenkaya, A., et al. (2015) Nature of the Empty States and Signature of the Charge Density Wave Instability and Upper Peierls Transition of TTF-TCNQ by Temperature-Dependent NEXAFS Spectroscopy. The European Physical Journal B, 88, 13.
https://doi.org/10.1140/epjb/e2014-50481-9 - 14. Khanna, S.K., Pouget, J.P., Comes, R., Garito, A.F. and Heeger, A.J. (1977) X-Ray Studies of 2kF and 4kF Anomalies in Tetrathiafulvalene-Tetracyanoquinodimethane (TTF-TCNQ). Physical Review B, 16, 1468.
https://doi.org/10.1103/PhysRevB.16.1468 - 15. Andronic, S., Casian, A. and Dusciac, V. (2015) Peierls Structural Transition in Q1D Crystals of TTF-TCNQ Type for Different Values of Carrier Concentration. Materials Today: Proceedings, 2, 3829-3835.
- 16. Andronic, S. and Casian, A. (2016) Phonons near Peierls Structural Transition in Quasi-One-Dimensional in organic crystals of TTF-TCNQ. Advances in Materials Physics and Chemistry, 6, 98-104.
https://doi.org/10.4236/ampc.2016.64010 - 17. Reitschel, H. (1973) The Giant Kohn Anomaly in a Peierls Semiconductor. Solid State Communications, 13, 1859.
- 18. Bulaevskii, L.N. (1975) Peierls Structure Transition in Quasi-One-Dimensional Crystals. Soviet Physics Uspekhi, 18, 131.
https://doi.org/10.1070/PU1975v018n02ABEH001950 - 19. Casian, A. (2006) Thermoelectric Properties of Electrically Conducting Organic Materials. In: Rowe, D.M., Ed., Thermoelectric Handbook, Macro to Nano, Chap. 36, CRC Press, Boca Raton.
- 20. Casian, A. and Sanduleac, I. (2014) Thermoelectric Properties of Tetrathiotetracene Iodide Crystals: Modeling and Experiment. Journal of Electronic Materials, 43, 3740-3745.
https://doi.org/10.1007/s11664-014-3105-6 - 21. Casian, A.I., Pflaum, J. and Sanduleac, I.I. (2015) Prospects of Low Dimensional Organic Materials for Thermoelectric Applications. Journal of Thermoelectricity, 1, 16.
- 22. Casian, A. and Sanduleac, I. (2015) Thermoelectric Properties of Nanostructured Tetrathiotetracene Iodide Crystals: 3D Modeling. Materials Today: Proceedings, 2, 504-509.
- 23. Casian, A., Dusciac, V. and Coropceanu, Iu. (2002) Huge Carrier Mobilities Expected in Quasi-One-Dimensional Organic Crystals. Physical Review B, 66, Article ID: 165404.
https://doi.org/10.1103/PhysRevB.66.165404 - 24. Casian, A. (2010) Violation of Wiedemann-Franz Law in Quasi-One-Dimensional Organic Crystals. Physical Review B, 81, Article ID: 155415.
https://doi.org/10.1103/physrevb.81.155415 - 25. Zubarev, D.N. (1960) Two-Dimensional Green Functions in Statistical Physics. Soviet Physics Uspekhi, 3, 320-362.
https://doi.org/10.1070/PU1960v003n03ABEH003275 - 26. Mortensen, K., Fabre, J.M. and Conwell, E.M. (1983) Thermopower Studies of a Series of Salts of Tetramethyltetrathiafulvalene [(TMTTF)2X, X = Br, ClO4, NO3, SCN, BF4, AsF6, and PF6. Physical Review B, 28, 5856.
https://doi.org/10.1103/PhysRevB.28.5856








