Advances in Materials Physics and Chemistry
Vol.05 No.08(2015), Article ID:58955,11 pages
10.4236/ampc.2015.58032
Minimum Amounts of Extracting Solvent of (A1A2∙∙∙At−1)/(A2A3∙∙∙At) Countercurrent Extraction Separation
Fu-Xiang Cheng1, Sheng Wu1,2, Song-Ling Wang1, Bo Zhang1, Yan Liu1, Chun-Sheng Liao1,2*, Chun-Hua Yan2
1China Minmetals (Beijing) Research Institute of RE Co., Ltd., Beijing, China
2Beijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, PKU-HKU Joint Lab on Rare Earth Materials and Bioinorganic Chemistry, Peking University, Beijing, China
Email: *cfx@cre-ol.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 July 2015; accepted 18 August 2015; published 21 August 2015
ABSTRACT
Minimum amounts of extracting solvent and scrubbing agent solution (denoted as Smin and Wmin respectively) mean the theoretical minimal requirements for chemicals to achieve a specified separation duty, and therefore attract more concerns in the process design of countercurrent extraction separation. Over the past decade, hyperlink extraction technology has been widely used in rare earth separation industry in China with the target to decrease chemical consumption as well as pollution discharges. However, the equations of Smin and Wmin derived in the earlier version of the theory of countercurrent extraction can only be correctly applied to two-component separation and become invalid for hyperlink processes. It is significant to develop new aspects of the theory for design of the hyperlink processes. The separation of (A1A2∙∙∙At−1)/(A2A3∙∙∙At) is the basic configuration in the hyperlink processes differently from in conventional processes, where A1, A2, ∙∙∙, At represent different kinds of rare earth ions with the same number of valence. The separations of two and three components have been discussed and the equations of Smin and Wmin are derived in our previous works. Nevertheless, it is still significant, especially for rare earth separations, to investigate the separations with more components. The present article will therefore focus on developing new expressions for Smin and Wmin applied to the (A1A2∙∙∙At−1)/(A2A3∙∙∙At) separation. Also a five-component separation case is simulated according to the derived equations. This work is an essential part of the new theory to design the hyperlink extraction processes.
Keywords:
Theory of Countercurrent Extraction, Minimum Amount of Extracting Solvent, Countercurrent Extraction, Hyperlink Process, Multi-Component Separation

1. Introduction
Rare earth separation processes of solvent extraction may involve as many as fifteen components. As the rare earths are all so close to each other in terms of extraction chemistry, the techniques by countercurrent extraction and scrubbing of the extract have been proved essential for the production of pure rare earth products [1] - [3] . Various methods such as McCabe-Thiele method [3] - [6] , chemical thermodynamics analysis [7] [8] , and mathematical empirical methods [9] [10] , have been developed to carry out the calculation and optimization of countercurrent extraction processes of rare earths. The remarkably rapid progress on separation processes of rare earths was created by the Theory of Countercurrent Extraction (called hereafter as “the theory” for simplicity unless otherwise specified) established by Xu et al. [11] [12] in 1970s. The theory derived a number of new algebra equations as well as flexible calculation approaches for process optimization. In particular, the theory facilitated the advent of one-step scale-up technique [13] , as a result of which the world rare earth industry encountered “China Impact” [14] .
Currently due to the increasing environmental concerns, the separation techniques of solvent extraction are tending to reduce both consumption and emission of chemicals [15] - [17] . Acidic extractants are commonly used to separate rare earths [1] [18] [19] , and saponification by basic substances is usually necessary for the purpose of increasing and stabilizing the extraction capacity of the acidic extractants. Meanwhile, inorganic acids are demanded for both scrubbing and stripping. Thus acids and bases are the main consumed chemicals, and the resulted salts are the main pollution during rare earth separation processes. To determine the theoretical minimum requirement of the base for saponification and the acid for scrubbing, the terms of minimum amounts of extracting solvent and scrubbing agent solution (denoted hereafter as Smin and Wmin respectively) are introduced respectively.
Hyperlink extraction technique has been developed and widely used in Chinese rare earth separation industry due to its virtue in reducing both consumptions and emissions since the early of last decades [14] [20] . By arranging two separation cascade units to offer each other with the extracting solvent or the scrubbing agent solution containing rare earths, the technique can decrease the consumption of acid or base for both of the two units. So far, the optimized parameters of a hyperlink process are determined by screening a great deal of simulation results [21] - [23] . However, the simulation cannot exactly tell the theoretical minimum values of parameters, and also the simulation task is too technical for common technicians. Therefore we are exploring to develop new aspects of the theory available for design of the hyperlink processes. Differently from the configuration of (A1A2∙∙∙Ak)/(Ak+1Ak+2∙∙∙At) (1 < k < t) commonly seen in conventional processes, (A1A2∙∙∙At−1)/(A2A3∙∙∙At) is the basic separation configuration in hyperlink processes [20] , where t ( ≥ 3) represents the number of components. The values of Smin and Wmin are the primary concerns for a given separation duty, and therefore in our previous works [24] - [27] , we discussed the separations with two or three components and derived the equations of Smin and Wmin. Nevertheless, rare earth separations involve more than 3 components in most cases, and thus in this article we will derive the equations of Smin and Wmin for multi-component separations with the (A1A2∙∙∙At−1)/ (A2A3∙∙∙At) configuration.
2. Description of the Separation System
Figure 1 displays a typical countercurrent extraction cascade unit with the separation configuration of (A1A2∙∙∙At−1)/(A2A3∙∙∙At), where t ( ≥ 3) means the number of components and A1, A2, ∙∙∙, At represents t kinds of trivalent rare earth ions in the feed with a prior extractable sequence of A1 > A2 > ∙∙∙ > At. The feed flowrates of the t components are f1, f2,∙∙∙, and ft (hereafter in mole per unit time) respectively all the time, where f1 + f2 + ∙∙∙ + ft = f. The separation factor of the neighboring Ai/Ai+1 (t > i ≥ 1) pair is denoted as βi/i+1; the separation factor of Ai/Ai+j pair (t > i ≥ 1; t - i ≥ j ≥ 1), βi/i+j, can be calculated according to:
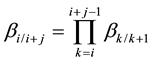 (1)
(1)
Figure 1. Schematic diagram for the countercurrent extraction cascade of hyperlink processes.
The separation cascade couples n extraction stages and m scrubbing stages. The partly saponified barren solvent with the flowrate S and hydrochloric acid with the flowrate W enter at opposite ends of the cascade, serving as extracting solvent and scrubbing agent solution respectively. Here for brevity the term “extracting solvent” is used to include solvent mixtures. The feed stream enters either stage n or stage (n + 1) depending on its phase type, as shown in Figure 1. The final raffinate and the final extract, which can behave as the feed in subsequent countercurrent units for further separation, contain no A1 or no At respectively as required.
It is assumed that the extracting solvent and the aqueous solution are immiscible and remain so at all cases of the operation. It is assumed that each stage is an equilibrium stage, and therefore all the flowrates are out of each stage in equilibrium. It is also assumed that only the saponified extractant has the extraction capacity with a single cation-exchange mechanism. The saponified extracting solvent is assumed to be always saturated with components when leaving all stages except (n + m)th stage. All the H + ion in the starting scrubbing acid is supposed to immediately exchange and migrate towards the organic phase after entering the cascade, and therefore the scrubbing agent solution has contained no acid since leaving (n + m)th stage. And also as all the components has a same number of valence, the mixed extraction factor which denotes the ratio of the total mole amount of all the components in the organic phase to that in the aqueous phase will keep constant either through extraction stages except stage 1 or through scrubbing stages except stage (n + m).
3. Expressions of Adjacent Stage Impurity
To derive the equation of Smin and Wmin, we need to introduce a term Adjacent Stage Impurity Ratio (briefly as ASIR) for the case of multi-component separation [24] as we did before [25] - [27] . The separation goal can be achieved by stepwise impurity removal in the countercurrent extraction cascade, and ASIR is then defined as Equation (2) which can evaluate the purification efficiency of a certain stage.
 (2)
(2)
where g denotes ASIR. The subscripts i and k represent an impurity and a stage, respectively. The gi,k then means ASIR of impurity Ai at stage k, and so hereafter.
In the extraction stages in Figure 1, the extracting solvent should withdraw component A1 stage by stage to obtain the final raffinate with no A1, and therefore component A1 is regarded as the impurity of the aqueous phase in the extraction section. Instead, component At behaves as the impurity in the organic phase to be removed by scrubbing agent solution in the scrubbing stages. Figure 2 shows the equilibrium flows of a continuous three stages, where x and y denote the flowrates of a component in the aqueous and the organic phases respectively. The subscripts i and k represent a component and a stage again, respectively. The xi,k then represent the flowrates of component Ai in the aqueous phase, and so hereafter. If 1 < k < n, which means that the three stages locate in extraction section, extraction equilibrium and mass balance in view of kth and (k + 1)th stages give the relations of Equations (3), (4) and (5).
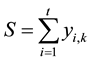 (3)
(3)
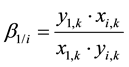
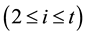 (4)
(4)
Figure 2. Mass flows in a continuous three stages.
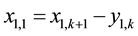 (5)
(5)
where x1,1 means the flowrates of A1 in the final raffinate, which should be approximate to zero according to the separation goal. From Equations (3) and (4), we have Equation (6).
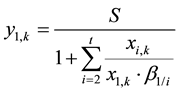 (6)
(6)
Substituting the expression for y1,k as in Equation (6) into Equation (5) gives Equation (7).
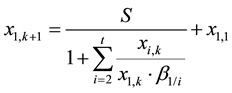 (7)
(7)
Thus the ASIR of component A1 at stage k of the extraction section, denoted by g1,k, can be expressed as the following equation:
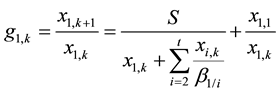 (8)
(8)
As the total aqueous flowrate,
 , should have an unchanged value through the extraction stages with the
, should have an unchanged value through the extraction stages with the
exception of stage 1 according to the constant-mixed-extraction-factor assumption mentioned before, and also the cation exchange reaction takes place always between a more extractable ion in the aqueous phase and a less extractable ion in the organic phase,
 as well as x1,k will decrease with stage from the central feed stage
as well as x1,k will decrease with stage from the central feed stage
towards the left end of the cascade, and consequently the ASIR of impurity A1 will exhibit an increasing tendency towards this direction.
In the scrubbing stages, the same analysis can give the expression for ASIR of impurity At as Equation (9) on the basis of extraction equilibrium and mass balance in view of (k − 1)th stage and kth stage where (n + 1) < k ≤ (n + m) in Figure 2.
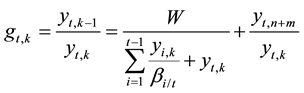 (9)
(9)
in which yt,n+m represents the flowrate of impurity At leaving the organic outlet in stage (n + m). From the same consideration as above, ASIR of impurity At should also present an increasing tendency with stage from the feed stage to stage (n + m) according to Equation (9).
ASIR presents an intuitive view of the status to remove an impurity in a separation cascade. Generally ASIR should have a value larger than 1 in order to perform purification stage by stage. Nevertheless when the extracting solvent or scrubbing agent solution loses their concentration driving force to withdraw the impurity from the opposite liquid phase at a certain stage, the value of ASIR will drop to 1 there. However, ASIR is always not smaller than 1.
4. Derivation of the Equations of Smin and Wmin
4.1. Principle Procedures of Deviation
For more accessible, the derivation procedures are outlined as the following before the details are presented.
Firstly, we need to know the conditions where both S and W have their theoretical minimum values to achieve a specified separation duty as shown in Figure 1. ASIR analysis can help to find out such conditions. When an S lower than Smin is given to the cascade, the two following events will occur in extraction section if this section is long enough: (i) more impurity A1 than required exists in the final raffinate; (ii) ASIR at some continuous extraction stages next to scrubbing section drops to 1. In this case, adding more extraction stages cannot decrease A1 in the raffinate any longer. Then if S is gradually increased, impurity A1 will become less and less in the final raffinate, while the event (ii) will remain until impurity A1 completely disappears in the final raffinate. Therefore it can be addressed that Smin should correspond to the S causing impurity A1 in the final raffinate just removed to the required level while the lowest value of ASIR in the extraction section still remaining at 1. Similarly, Wmin should be the W that can just reduce impurity At in final extract to the required level, and meanwhile there are some continuous stages with ASIR of 1 next to extraction section.
Secondly based on the above conditions, flowrate analysis is taken on the extraction and the scrubbing sections separately. We can deduct the expressions for both the aqueous and the organic flowrates of all components leaving stage n except for impurity A1. The flowrates of each intermediate component are temporarily expressed with its flowrate in final raffinate which still remains unknown now. Similarly we will also deduct the expressions for both the aqueous and organic flowrates of each component leaving stage (n + 1) except for impurity At, and the flowrate expressions of each intermediate component here involve its unknown flowrate in the final extract.
In the third step, we will consider the mass balance between stage n and stage (n + 1) which connect the extraction and the scrubbing sections. As a result, we can obtain the quantitative relationships between the two flowrate expressions of each intermediate component leaving stage n and stage (n + 1) as well as the ratio of the flowrates of each intermediate component leaving the two opposite ends consequently. Taking the mass balance of each component in the two ends into account, the exiting flowrates of each component in the two ends can then become known.
Finally the equations of Smin and Wmin can be derived according to Equations (8) and (9) with the use of the flowrate expressions obtained in the steps above.
4.2. Conditions of Smin and Wmin
Mass balance of the (A1A2∙∙∙At−1)/(A2A3∙∙∙At) separation duty suggests the quantitative relations as the following expressions.
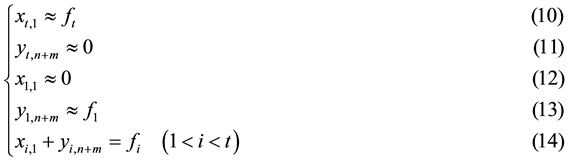
where xi,1 and yi,n+m represent two exiting flowrates of Ai (1 ≤ i ≤ t) in the aqueous and the organic streams, respectively. If stage k is an extraction stage and has the ASIR value of 1, according to the definition of ASIR, we know that
 (15)
(15)
And taking the mass balance of A1 represented by Equation (16) into account, we can obtain Equation (17).


Equation (17) reveals that the aqueous and the organic flowrates of impurity A1 leaving one equilibrium extraction stage with ASIR of 1 should be equal to each other. In this case the extraction equilibrium relations between A1 and the other components in the kth stage can be reduced as

Moreover according to the constant-mixed-extraction-factor assumption, when an aqueous stream is used as feed, the overall flowrates of all components in the aqueous and the organic phases should always be (f + W) and S respectively when leaving an extraction stage with the exception of 1st stage. If it is also assumed that the extraction section of the cascade is long enough and there are at least (t − 2) continuous extraction stages including the feed stage (stage n) with the same ASIR value of 1, a series of relationships can be noted as below in view of mass balance within these stages.
where u = n - t + 3; expressions (20) and (21) are two collectives of (t - 2) and (t2 - 4t + 3) equations respectively, and therefore expressions (19), (20) and (21) consist of a system involving (t2 - 3t + 2) independent equations. Then we analyze the number of the unknowns involved in this equation system. As all of these (t - 2) stages have ASIR value of 1, the aqueous flowrates of impurity A1 leaving these stages (i.e., x1,u+j) remain unvaried, and thus y1,u+j is also unvaried as it always equals x1,u+j in these (t - 2) stages. Moreover, the aqueous exiting flowrates of each component, xi,1 (1 ≤ i ≤ t), will not change with time as the cascade is in a steady state, and they can therefore be treated as constant terms. Thus in the equation system, only yi,u+j (2 ≤ i ≤ t; 0 ≤ j ≤ t-3) are regarded as unknown quantities, with the number of (t2 − 3t + 2) which is just same as that of the independent equations. Solving the equation system enables us to express all yi,u+j with the involved constant terms W, S, β1/i (2 ≤ i ≤ t ), xi,1(2 ≤ i ≤ t) and y1,n. Furthermore, when more continuous extraction stages than (t − 2) have ASIR of 1, any continuous (t - 2) extraction stages among them should have a same group of solutions. To satisfy this condition, it is necessary for the organic flowrate of each component to have the same value when leaving any extraction stage involved in these stages with ASIR of 1, and accordingly the aqueous flowrate of each component also remains constant when leaving these stages, which means yi,n = yi,n−1 = ∙∙∙ = yi,u−1 and xi,n = xi,n−1 = ∙∙∙ = xi,u−1 (1 ≤ i ≤ t). Working the case using an organic stream as starting feed in the same manner, we can address the same conclusion.
4.3. Separate Analysis of Extraction and Scrubbing Sections
Figure 3 displays the material flows of four continuous stages, where the aqueous or the organic feed will flow into nth stage or (n + 1)th stage in Figure 3, respectively. According to the theory of countercurrent extraction [12] , the stage receiving an aqueous feed is generally treated as an extraction stage, whereas the stage that an organic feed enters is regarded as a scrubbing stage instead, as illustrated in Figure 1.
When there are (t − 1) or more extraction stages with ASIR of 1 next to scrubbing section, the mass balance on Interface I between (n − 1)th and nth stages in Figure 3 can be expressed as the following three equations.
Considering that xi,n and yi,n in Equation (23) as well as xt,n and yt,n in Equation (24) should satisfy Equation (18) by letting k = n, we can obtain (t − 1) equation systems, and each of them involves two unknowns xi,n and yi,n (2 ≤ i ≤ t) as well as two independent equations. Solving these equation systems gives the expressions of the aqueous and the organic flowrates of A2, A3, ∙∙∙, At leaving stage n as follows.
Figure 3. Mass flows near feed stage.
Equations (25) and (26) specify the lowest requirement on the aqueous flowrate of each component leaving the feed stage in order to reach its exiting aqueous flowrate as required respectively by Equations (23) or (24).
To derive the equation of Smin from Equation (8), we should turn to analyze the scrubbing section to obtain the expressions for the flowrates of A1 as well as xi,1 (2 ≤ i ≤ t - 1). In scrubbing section, when there are more stages than (t - 2) involving stage (n + 1) with ASIR of 1, the analysis in exactly the same manner as in extraction section can reveal that the aqueous and the organic flowrates of each component do not vary with stage in these stages. Therefore the mass balance on interface III in Figure 3 can provide the relations below, similarly to Equations (22)-(24).
The expressions of extraction equilibrium between At and other components according to Equation (31) can be simplified to result in

Furthermore, by constructing and then solving (t − 1) equation systems involving two independent equations and two unknowns xi,n+1, yi,n+1 (1 ≤ i ≤ t − 1) respectively according to Equations (29), (30) and (32), we can obtain the expressions for the aqueous and the organic flowrates of A1, A2, ∙∙∙, At−1 leaving (n + 1)th stage as presented in Equations (33)-(36), similarly to Equations (25)-(28).
4.4. Combining Analysis of Extraction and Scrubbing Sections
The relations of Equations (22)-(36) can apply to the cases of using either the aqueous feed or the organic feed. Nevertheless, the different mass balance of all components on interface II in Figure 3 will occur if different feed is used, as expressed in Equations (37)-(39) for aqueous feed and Equations (40)-(42) for organic feed, where 2 ≤ i ≤ t − 1.
In the case of using an aqueous stream as feed, the comparison of Equation (30) and Equation (38) gives

and thus by substituting Equation (27) for yi,n as well as Equation (36) for yi,n+1 and rearrangement, we have

Equation (44), termed by us as optimal flowrate ratio equation of intermediate components, gives the optimal ratio between its flowrates leaving two opposite outlets when both of Smin and Wmin are applied to the (A1∙∙∙At−1)/(A2∙∙∙At) separation system using an aqueous feed. It can be found from Equation (44) that the optimal flowrate ratio of an intermediate component, such as Ai, is determined only by β1/i and βi/t (Note: β1/t = β1/I × βi/t), but independent of the separation factors of other pairs as well as the composition of the initial feed.
Further, by combining Equation (14) with Equation (44) and simultaneously solving them, we can immediately obtain the optimal flowrate equations of intermediate components as expressed by Equations (45) and (46). The equations permit us to calculate the exiting flowrates of each intermediate component when both Smin and Wmin are given to the specified separation cascade.
From Equations (17) and (43), the relations x1,n = y1,n = y1,n+1 can be easily found when using the aqueous feed, and then taking Equation (35) into account can lead to Equation (47); introduction of the expression for xi,1 as in Equation (45) into Equation (25) results in Equation (48); and for the convenience of comparison, Equation (26) is listed after Equation (48) as below. It is worthwhile to notice from Equations (47), (48) and (26) that the aqueous stream leaving the feed stage has a composition exactly the same as the initial aqueous feed.
The analysis in the same manner will be applied when an organic feed is used. The combination of Equation (23) with Equation (41) leads to

Then the optimal flowrate ratio equation as well as the optimal flowrate equations for the separation system using organic feed can be derived respectively as Equation (50) and Equations (51), (52) respectively, and the organic flowrates of all components leaving the feed stage can be obtained and summarized as Equations (35), (53), (54).

Equations (35), (53) and (54) clearly indicate that the composition of the organic stream leaving the feed stage is exactly the same as that of the initial organic feed.
4.5. Derivation of Smin and Wmin Equations
The equation of Smin for the (A1A2∙∙∙Ak)/(Ak+1Ak+2∙∙∙At) separation using aqueous feed can be derived as Equation (55) by introducing Equations (47), (48), (26) into Equation (8) and using the conditions of g1,n = 1 and x1,1 = 0.

Then taking the mass balance in the organic outlet as given by Equation (56) into account, we will have the expression for Wmin as in Equation (57) by replacing Smin and yi,n+m in Equation (56) with Equation (55) and Equation (46) respectively and rearranging it, if the total feed flowrate is unity, that is, f = f1 + f2 + ∙∙∙ + ft = 1.


Also, Equation (57) can be derived by introducing the organic flowrates of all components leaving feed stage, as expressed by Equation (35), (53) and (54) into Equation (9) and making gt,n+1 = 1 as well as neglecting the second item. Similarly the expressions of Smin and Wmin for organic feed system can be derived as follows:


5. Case Study
Calculation of Parameters
The results above were used to design a separation of an aqueous solution containing Ho, Er, Tm, Yb and Lu with the (HoErTmYb)/(ErTmYbLu) separation configuration. Equal volumes of HEH(EHP) and refined kerosene, partly saponified by NaOH, consists of the starting organic phase, and 4.0 mol∙L−1 hydrochloric acid is used as a starting scrubbing agent solution, as the common cases in industry. The separation factors [12] [19] between the neighboring components involved in the feed together with their feeding flowrates are listed in Table 1. The exiting aqueous flowrate of Lu and organic flowrate of Ho, xLu,1 and yHo,n+m, were determined on the basis of the total required purity (99.99%) of (HoErTmYb) in the exiting aqueous stream and that of (ErTmYbLu) in the exiting organic stream, respectively. The exiting flowrates of all intermediate components could then be calculated according to Equations (45) and (46) with the use of the data in Table 1 and summarized in Table 2. Then Smin and Wmin could be calculated as 0.2639 and 0.0176 according to Equation (55) and Equation (57), respectively.
Self-developed software [22] [23] was used to conduct static simulation of the five-component separation described above. Based on mass balance and extraction equilibrium, the calculation was started from two opposite ends stagewise towards centre simultaneously until there were enough stages where ASIR dropped to 1 for each side. Figure 4 displays the varied compositions of the aqueous and organic streams in addition to ASIR with stage through the cascade according to the calculation results. It can be seen from Figure 4(c) that ASIR in some stages on both sides of the feed stage (95th stage) has approached to 1 and accordingly the flowrates of all components do not change within these stages as shown in both Figure 4(a) and Figure 4(b), which implies that the driving force of both extracting solvent and scrubbing agent solution for separation has been used up here. Moreover also from Figure 4(a) the rare earth composition in the aqueous stream near the feed stage is exactly same as that in the initial aqueous feed, which is also in accordance with the conclusion deducted earlier in the present article.
6. Conclusions
As the basic separation configuration of hyperlink extraction process, (A1A2∙∙∙At−1)/(A2A3∙∙∙At) separation was
Figure 4. Variations with stage of (1) composition in aqueous phase; (2) composition in organic phase; (3) ASIR.
Table 1. Parameters for a five-component separation.
Table 2. Calculated exiting flowrates of all components.
discussed with regard to the determination of the minimum amounts of extracting solvent and scrubbing agent solution (Smin and Wmin), and some conclusions had been drawn as follows:
(1) Both Smin in the case of using an aqueous feed and Wmin in the case of using an organic feed can be expressed by feed composition together with the separation factors between the components involved, whereas both Wmin and Smin in the corresponding cases are only determined by the separation factor between the most and the least extractable components, but independent of either separation factors of other pairs or feed composition.
(2) For any intermediate component, when Smin and Wmin are applied to the cascade with enough stages, the ratio of its flowrates leaving two opposite outlets is decided by an optimal flowrate ratio equation. This ratio can be expressed only in terms of the separation factors between the intermediate component and the two end components, and do not involve separation factors of other pairs as well as the feed composition, in spite of the different forms when different kinds of feed are used.
(3) Whichever kind of feed is used, when Smin and Wmin are applied to a cascade with enough stages, the stream of same kind as feed should have the same composition as the initial feed when leaving the feed stage, which provides a proof for the feed-stage-composition assumption proposed in the early version of the theory of countercurrent extraction.
Acknowledgements
This research was supported by the National Basic Research Program of China (973) (2012CBA01200).
Cite this paper
Fu-XiangCheng,ShengWu,Song-LingWang,BoZhang,YanLiu,Chun-ShengLiao,Chun-HuaYan, (2015) Minimum Amounts of Extracting Solvent of (A1A2···At-1)/(A2A3···At) Countercurrent Extraction Separation. Advances in Materials Physics and Chemistry,05,325-336. doi: 10.4236/ampc.2015.58032
References
- 1. Brown, C.G. and Sherrington, L.G. (1979) Solvent Extraction Used in Industrial Separation of Rare Earths. Journal of Chemical Technology and Biotechnology, 29, 193-209.
http://dx.doi.org/10.1002/jctb.503290402 - 2. Thakur, N.V. (2000) Separation of Rare Earths by Solvent Extraction. Mineral Processing and Extractive Metallurgy Review, 21, 277-306.
http://dx.doi.org/10.1080/08827500008914171 - 3. Xie, F., Zhang, T.A., Dreisinger, D. and Doyle, F. (2014) A Critical Review on Solvent Extraction of Rare Earths from Aqueous Solutions. Minerals Engineering, 56, 10-28.
http://dx.doi.org/10.1016/j.mineng.2013.10.021 - 4. Zhu, T. (1991) Solvent Extraction in China. Hydro-metallurgy, 27, 231-245.
http://dx.doi.org/10.1016/0304-386X(91)90069-X - 5. Rydberg, J., Cox, M., Musikas, C. and Choppin, G.R. (2004) Solvent Extraction Principles and Practice. 2nd Edition, CRC Press, Florida.
http://dx.doi.org/10.1201/9780203021460 - 6. Radhika, S., Kumar, B.N., Kantam, M.L. and Reddy, R.B. (2011) Solvent Extraction and Separation of Rare-Earths from Phosphoric Acid Solutions with TOPS 99. Hydrometallurgy, 110, 50-55.
http://dx.doi.org/10.1016/j.hydromet.2011.08.004 - 7. Hoh, Y.-C. and Bautista, R.G., (1979) Liquid-Liquid Extraction Equilibrium Models for Binary and Ternary Lanthanides-HDEHP Systems. Industrial and Engineering Chemistry Process Design and Development, 18, 446-453.
http://dx.doi.org/10.1021/i260071a017 - 8. Ryu, K.H., Lee, C.K., Lee, G.-G., Jo, S.K. and Sung, S.W. (2013) Modeling and Simulation of Solvent Extraction Processes for Purifying Rare Earth Metals with PC88A. Korean Journal of Chemical Engineering, 30, 1946-1953.
http://dx.doi.org/10.1007/s11814-013-0135-3 - 9. Giles, A.E., Aldrich, C. and Van Deventer, J.S.J. (1996) Modeling of Rare Earth Solvent Extraction with Artificial Neural Nets. Hydrometallurgy, 43, 241-255.
http://dx.doi.org/10.1016/0304-386X(95)00098-2 - 10. Anitha, M. and Singh, H. (2008) Artificial Neural Network Simulation of Rare Earths Solvent Extraction Equilibrium Data. Desalination, 232, 59-70.
http://dx.doi.org/10.1016/j.desal.2007.10.037 - 11. Xu, G.X., Li, B.G., Yan, C.H., Zhang, L.P. and Hao, H.M. (1985) Theory of Countercurrent Extraction and Its Applications in Rare Earth Extraction Industry. In: Xu, G.X., Ed., New Frontiers in Rare Earth Science and Applications, Science Press, Beijing, 429-437.
- 12. Xu, G.X. (1995) Chapter 8: Rare Earths. Metallurgical Industry Press, Beijing. (In Chinese)
- 13. Yan, C.H. (1988) One-Step Scale-Up of Rare Earth Extraction Separation Process. Doctoral Dissertation, Peking University, Beijing. (In Chinese)
- 14. Yan, C.H., Jia, J.J., Liao, C.S., Wu, S. and Xu, G.X. (2006) Rare Earth Separation in China. Tsinghua Science & Technology, 11, 241-247.
http://dx.doi.org/10.1016/S1007-0214(06)70183-3 - 15. Feng, Z.Y., Huang, X.W., Liu, H.J., Wang, M., Long, Z.Q., Yu, Y. and Wang, C.M. (2012) Study on Preparation and Application of Novel Saponification Agent for Organic Phase of Rare Earths Extraction. Journal of Rare Earths, 30, 903-908.
http://dx.doi.org/10.1016/S1002-0721(12)60152-5 - 16. Han, Q.Y. (2013) Technical and Economical Evaluation on Separation Process of Light Rare Earth. Journal of the Chinese Society of Rare Earths, 31, 399-404. (In Chinese)
- 17. Xiao, Y.F., Long, Z.Q., Huang, X.W., Feng, Z.Y., Cui, D.L. and Wang, L.S. (2013) Study on Non-Saponification Extraction Process for Rare Earth Separation. Journal of Rare Earths, 31, 512-516.
http://dx.doi.org/10.1016/S1002-0721(12)60311-1 - 18. Moeller, T., Martin, D.F., Thompson, L.C., Ferrus, R., Feistel, G.R. and Randall, W.J. (1965) The Coordination Chemistry of Yttrium and the Rare Earth Metal Ions. Chemical Reviews, 65, 1-50. http://dx.doi.org/10.1021/cr60233a001
- 19. Sato, T. (1989) Liquid-Liquid Extraction of Rare-Earth Elements from Aqueous Acid Solutions by Acid Organophosphorus Compounds. Hydrometallurgy, 22, 121-140.
http://dx.doi.org/10.1016/0304-386X(89)90045-5 - 20. Liao, C.S., Wu, S., Cheng, F.X., Wang, S.L., Liu, Y., Zhang, B. and Yan, C.H. (2013) Clean Separation Technologies of Rare Earth Resources in China. Journal of Rare Earths, 31, 331-336.
http://dx.doi.org/10.1016/S1002-0721(12)60281-6 - 21. Wu, S., Liao, C.S. and Jia, J.T. (2003) Chinese Software Registration. Register No. 2003SR4279.
- 22. Wu, S., Liao, C.S., Jia, J.T. and Yan, C.H. (2004) Static Design for Multiple Components and Multiple Outlets Rare Earth Countercurrent Extraction (I): Algorithm of Static Design. Journal of the Chinese Society of Rare Earths, 22, 17-21. (In Chinese)
- 23. Wu, S., Liao, C.S., Jia, J.T. and Yan, C.H. (2004) Static Design for Multi-Component and Multi-Outlet Rare Earth Countercurrent Extraction (II): Static Design and Its Verification. Journal of the Chinese Society of Rare Earths, 22, 171-176. (In Chinese)
- 24. Cheng, F.X., Wu, S., Liao, C.S. and Yan, C.H. (2013) Adjacent Stage Impurity Ratio in Rare Earth Countercurrent Extraction Process. Journal of Rare Earths, 31, 169-173.
http://dx.doi.org/10.1016/S1002-0721(12)60253-1 - 25. Cheng, F.X., Wu, S., Liu, Y., Wang, S.L., Zhang, B., Liao, C.S. and Yan, C.H. (2014) Minimum Amount of Extracting Solvent for AB/BC Countercurrent Separation Using Aqueous Feed. Separation and Purification Technology, 131, 8-13.
http://dx.doi.org/10.1016/j.seppur.2014.04.031 - 26. Cheng, F.X., Wu, S., Zhang, B., Liu, Y., Wang, S.L., Liao, C.S. and Yan, C.H. (2014) Minimum Amount of Extracting Solvent of AB/BC Countercurrent Extraction Separation Using Organic Feed. Journal of Rare Earths, 32, 439-444.
http://dx.doi.org/10.1016/S1002-0721(14)60091-0 - 27. Cheng, F.X., Wu, S., Liu, Y., Wang, S.L., Zhang, B., Liao, C.S. and Yan, C.H. (2014) Minimum Amount of Extracting Solvent of a Separation of Two Rare Earth Components. Advances in Materials Physics and Chemistry, 4, 275-283.
http://dx.doi.org/10.4236/ampc.2014.412030
NOTES
*Corresponding author.


















