ABSTRACT

This paper discusses the theoretical validity of Thomas Piketty’s fundamental laws about income distribution in the context of a standard neoclassical growth model. We take Uzawa’s two-sector growth model as the platform of our analysis, as it allows us to make a distinction between the technological elasticity of factor substitution of the production function and the aggregate distributive elasticity of substitution. We examine the properties of the non-steady growth path through both analytical and numerical investigations. We conclude that some of the numerical simulations corroborate Piketty’s theory without assuming that the economy is on a steady growth path. However, if the elasticities of factor substitution in the individual sectors are less than one as many empirical studies show, then the economy approaches the state where all products are completely distributed to workers. This contradicts Piketty’s diagnosis about the current distributional inequality. In addition, the aggregate income distribution is stable for a relatively long time, and differences in the initial conditions are preserved during this period. This means that the comparative statics of the steady states might not present an adequate description of the economy’s behavior in a period of time that is practical. Our final evaluation of Piketty’s proposition is that it is better understood as a theory inferred from historical data and not one necessarily deduced from standard neoclassical growth theory.

Keywords:

Income Distribution, Two-Sector Growth Model, Technological Progress, Inequality, Factor Substitution

1. Introduction

This paper uses Uzawa’s two-sector model¹ with non-neutral technological progress to examine Thomas Piketty’s fundamental laws of capitalism proposed in his book Capital in the Twenty-First Century². His argument derived from the laws is that economic inequality will be accelerated when the growth rate of income decreases and the capital/output ratio increases. Although Piketty’s theory encompasses not only functional income distribution but also distribution of wealth and both of them are inseparably interwoven to explain the current distributional inequality in his book, we will restrict our scope of the argument to the long-run trend of functional distribution of income. Aggregate distribution of income between wages and profits is closely related to the macroeconomic investment―savings balance, and we will exclusively focus on this distributional mechanism. Given the present unequal distribution of wealth, however, “anything that increases between-inequality ... is very likely to increase overall inequality’’³.

We use a neoclassical model because Piketty himself employs some terms of neoclassical theory, such as the steady state, the elasticity of factor substitution and the production function, to demonstrate that economic inequalities do arise even in the framework of a standard neoclassical growth model. In fact, his second fundamental law of capitalism can be directly deduced from the Solow-type growth model⁴. We employ the two-sector model, because Piketty believes “the right model to think about rising capital-income ratios and capital shares in recent decades is a multi-sector model of capital accumulation, with substantial movements in relative prices, and with important variations in bargaining power over time’’⁵.

Although Piketty’s “sector’’ in this context encompasses a much wider variety of sectors, such as labor unions, than that of the neoclassical two-sector model, Uzawa’s formulation is, at least from a theoretical point of view, a natural extension toward a more general approach, because Piketty thinks that the difference in capital intensities among industries is important to understand the behavior of the aggregate capital/output ratio⁶. The two-sector model has only one kind of capital goods; however, the behaviors of the capital/output ratio and of the aggregate profit share, both of which constitute Piketty’s fundamental laws, are determined by technological conditions in the two sectors.

The two-sector model also enables us to make a distinction between the technological elasticities of factor substitution of the production function in the individual sectors and the aggregate distributive elasticities of substitution. These two kinds of elasticities are often confused with one another. The latter is simply another expression of the behavior of the aggregate distributive shares and is not determined solely by the technological elasticities of individual industries. Therefore, we believe that this is a necessary step toward a more general discussion of the functional distribution of aggregate income.

As well known, the one-sector version of the neoclassical growth model has the steady state, or the balanced growth path, if Inada’s derivative condition is satisfied, and the equilibrium is stable under the ordinary set of assumptions. However, if we introduce technological changes into the model, then the only type of technological progress that generally assures the existence of the steady state is Harrod neutral, unless the production function is a Cobb―Douglas type. Although we have abundant literature on induced technological progress, beginning with [7] , it is still difficult to conclude that every technological progress is always Harrod neutral. As Acemoglu demonstrated, the type of the technological progress is purely labor augmenting in the long run, but, on a trajectory to the steady growth path, it is typically capital augmenting. Therefore, purely Harrod neutral technological progress is only a long run phenomenon⁷. In addition, non-neutral technological progress has literally non-neutral effects on income distribution. Given these reasons, we need to analyze the economy with non-neutral technological progress and on a non-steady growth path. In this paper, we analyze the dynamic behavior of the economy under the assumption of non-neutral technological progress to verify Piketty’s theory for more general states of the economy that have no inner equilibrium⁸. Lacking any comparable equilibrium state within the finite space, we have to examine the dynamic process itself directly.

Using mainly comparative statics in his book, Piketty has to assume the steady growth rate of income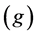, the average rate of savings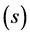, and the rate of return on capital 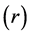as parameters so that he can argue that increasing the capital/output ratio 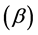will cause the profit share to increase according to his fundamental laws. However, in the real world, is closely connected to, which directly influences income distribution. This income distribution, in turn, is one of the major determinants of. Therefore, we treat them as endogenous variables in our dynamic analysis⁹.

Since we mainly focus on the state that has no inner equilibrium in the following argument, we have to investigate the properties of the dynamic trajectories directly. In the standard approach to analyze the dynamical property of the neoclassical growth models, we reduce all equations of the model to a single dynamic equation of the capital/labor ratio,. However, is defined in the right half-open interval of, and it converges on the origin or diverges to infinity when the model has no steady equilibrium within the space. In this case, it is rather difficult to discern the meaningful properties of the trajectories. Hence, we do not follow this standard procedure in this paper.

Instead, we reorganize the model by using the wage shares of each sector, because they stay in the closed interval of by definition, so that we can observe the behavior of trajectories infinitely in the finite quadratic space. Following this approach, we observe the dynamic behavior of the major variables such as the capital/output ratio, the aggregate elasticity of factor substitution, and so on and compare them with Piketty’s argument by using some numerical simulations. Our aim is not to trace the behavior of some real economy quantitatively but to perform qualitative comparisons of trajectories of the theoretical model. Therefore, we do not place much importance on the calibration of the parameters and the initial conditions.

2. Specification of the Model

We make Uzawa’s two-sector growth model with non-neutral technological progress the starting point of our analysis. The asymptotic trajectories of the neoclassical one- sector growth model with non-neutral technological progress are discussed in [10] [11] and [12] ¹⁰. As for the two-sector version of the asymptotic approach, only [13] and [14] are available to our knowledge. Lapan assumes a constant proportional savings rate and analyzes trajectories with Hicks neutral technological progress only in the investment goods sector first, and then with Harrod neutral technological progress in both sectors. He then analyzes the asymptotic behavior of the economy for those two cases. Our model is different in three respects from that of Lapan. First, we treat the aggregate savings rate as a variable. Second, we assume non-neutral exogenous technological progress in both sectors. Third, we directly observe the dynamic trajectories, but not the asymptotic ones. Our model is basically the same as that of [14] , but we mainly focus on the non-steady growth path and perform some numerical simulations to evaluate Piketty’s theory¹¹.

Since Uzawa’s model assumes the classical savings function, it is easy to manipulate the equations. However, there is more to this assumption; it allows us to treat the savings rate as an endogenous variable¹². If the savings rate from profits is larger than that from wages, the economy must distribute more income to capital owners to generate more savings when capital accumulation accelerates. This is the fundamental mechanism of macroeconomic income distribution¹³. We believe that any dynamic model of aggregate income distribution must incorporate this property of the economy.

Our model consists of 11 variables and five parameters as given below.

: Product of goods of the sector,

: Total labor force of the economy

: Labor input of the sector,

: Total capital stock of the economy

: Capital input of the sector,

: Rate of profit

: Price of consumption goods as evaluated by investment goods

: Real wage rate as evaluated by consumption goods

: Growth rate of the labor force*

: Rate of capital-augmenting technological progress in the sector, *

: Rate of labor-augmenting technological progress in the sector, *

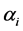
(Subscript 1 denotes the investment goods sector, and subscript 2 denotes the consumption goods sector. Parameters are marked with an asterisk in the above list. We assume all the parameters take a non-negative value.)

We assume that all markets in the economy are perfectly competitive and both the rate of profit and the real wage rate are completely arbitrated between the sectors. There is no idle capacity and no unemployed labor force in the economy.

is produced by using and in each sector under the given technology represented by the well-behaved production function with constant returns to scale¹⁴.

(1)

According to the marginal productivity theory, and are determined by the following equations.

(2)

(3)

Full utilization of capital equipment and full employment of the labor force are expressed as follows.

(4)

(5)

Since we assume the classical savings function, all profits are saved and all wages are consumed.

(6)

In the above two equations in (6), if either the left or the right one holds, the other is automatically satisfied, because the model follows Walras’ law, which suggests that the existence of excess supply in one market must be matched by excess demand in another so that it balances out. All products produced in the investment goods sector are devoted to capital formation of the economy, and the labor force grows at the rate of exogenously. Therefore, we have

(7)

and

(8)

Since the 11 equations given above contain 11 variables in total, our model is mathematically complete.

3. Existence and Stability of the Steady Growth Pathl

In this section, we derive conditions that satisfy Kaldor’s stylized facts before analyzing the case of non-steady growth. The stylized facts basically consist of the following four conditions.

a. Constant rate of profit.

b. Constant capital/output ratio.

c. Capital grows faster than the labor force.

d. Constant growth rate of labor productivity.

To determine the conditions under which the Kaldorian steady state exists, we integrate all the equations into the following three differential equations¹⁵.

(9)

(10)

and

(11)

where is the rate of capital growth; is the wage share of the sector; and is the elasticity of factor substitution of the sector. The elasticities of factor substitution and the other three symbols-, and -are defined as follows.

(12)¹⁶

(13)

(14)

(15)

where. As indicated in (15), the elasticity of

factor substitution is generally an endogenous variable. However, we have to specify the sign of the third derivative of the production function to define its dynamic behavior, but that seems to have no practical meaning in terms of economic theory. Therefore, we assume here that the elasticity of factor substitution in each sector is constant over time. This means that we implicitly assume a CES type production functions. If we consider as a constant, then the dynamic system defined by (9), (10) and (11) contains just three variables, and, and their dynamic behaviors are determined by the three equations.

For our model to have a growth path corresponding to Kaldor’s stylized fact, the value of (11) should be zero. Then, since equals under the assumption of the classical savings function, the above conditions a and c are satisfied. However, the steady growth rate for this case is

(16)

Since the right-hand side of this equation is a function of and, the growth rate of capital is constant through time only when the wage shares of both sectors are constant except for the case where they satisfy a specific relationship to keep the right-hand side of (16) zero over time.

Therefore, for the steady growth path to exist, the following three conditions should be satisfied:

(17)

(18)

and

(19)

under the following constraints for the solution to be an inner equilibrium.

It is evident from (17) that either or should be satisfied for to hold. We investigate conditions for the equilibrium of the other two variables according to each of these two cases.

(and)

Substituting into (18), we have

(20)

Therefore, for to satisfy, and/or must hold. When either of these two conditions holds, the equilibrium rate of growth, , which is equal to the equilibrium rate of profit, is. (and)

Following the same process as in the above case, we have

(21)

If either of these two conditions is satisfied, then, from (19), the growth rate becomes

(22)

As for the case of, is constant over time and we can treat it as a parameter. When the second condition of (21) holds, the right-hand side of (22) is also expressed by

(23)

Now, we have the following four cases for the existence of a steady-growth path. The first two conditions were derived by [19] . The first one implies that technological progress in the investment goods sector should be Harrod neutral and, if, the technological progress of the consumption goods sector should be Hicks neutral. The second one implies that technological progress in the investment goods sector should be Harrod neutral and the consumption goods sector should be characterized by the Cobb―Douglas production function, which keeps the distributive share of that sector constant. The third condition is self-evident. It means that both sectors should be characterized by the Cobb―Douglas production function. The last condition was derived by [14] . Even if technological progress is Harrod neutral in both sectors, i.e., , that is not sufficient to ensure the existence of a steady state. That is, should be satisfied.

Case a:

Case b:

Case c:

Case d:

Next, we look into the dynamic behavior of when either of these four conditions is satisfied. It is given by the following four equations for each case.

For Case a:

(24)

For Case b:

(25)

For Case c:

(26)

For Case d:

(27)

These four differential equations contain either or and. Since and must be subject to the condition that, the stability property of the positive equilibrium value of is determined solely by the last factor of the right-hand side of (24)-(27), , for all cases. For cases b, c, and d, is stable without any additional assumption, because the signs of the other factors are all positive. For case a, the dynamic property depends on the sign of. Let us substitute with in (12), where is the ratio of factor prices,. We then have the following relationship;

(28)

Since the denominator of this equation is obviously positive, we look into the sign of the numerator.

(29)

Therefore, if either of the following two conditions,

(30)

are satisfied, holds. These two sufficient conditions for stability are formally the same as those derived from Uzawa’s original model, which assumes no technological progress.

Figure 1 shows the dynamic process of. As shown in the figure, is unstable and is stable and economically meaningful.

The behavior of the capital/output ratio is determined by the following equation, where is the aggregate output of products expressed by the amount of investment goods, and is the capital/labor ratio for the economy as a whole.

(31)

From the above equation, it is evident that is constant over time when is constant on the equilibrium growth path, because is constant at. The behavior of is given by

(32)

Inputting the above four conditions of cases a, b, c, and d into (32), respectively, its value becomes zero for all cases, and that means is constant on the equilibrium

growth path.

Since, the behavior of output per capita is given by the following equation.

(33)

Therefore, it grows at the rate of.

For cases a and b, should be satisfied, and for the other two cases, should be satisfied so that capital grows faster than labor force.

If one of these four conditions is satisfied, we have a growth path corresponding to Kaldor’s stylized facts. However, in actual economies, there seems to be no need for every type of technological progress and the values of elasticity of factor substitution to satisfy always these strict conditions. Next, we investigate what behavior an economy exhibits in the case of non-steady growth.

4. Behavior of Non-Steady Growth Path

As evident from the forms of Equations ((9) and (10)), there are two additional cases of corner equilibria, even if the system has no inner equilibrium. If are given at either (1, 1) or (1, 0), they are stationary. It is also evident from the forms of these two equations that both and are not influenced by the behavior of in the vicinity of those two singular points, and that and behave independently of each other Therefore, we first assume that and are at one of those two points, and investigate the stability of. Then, we investigate the stability of the system as a whole.

The dynamic system for the two singular points is given by the following equations respectively.

Therefore, if a positive equilibrium exists, it is stable in the vicinity of or.

Case 1.

Let and in (19), the stable equilibrium value of is given by the following equation:

(34)

Therefore, we assume the parameters in (34) take values that satisfy to guarantee the existence of a positive equilibrium growth path.

The Jacobian of the system given by (9), (10), and (11) evaluated at is as follows.

(35)

It is evident from the array of elements in this matrix that the trajectories of and are, as we have already mentioned above, independent of in the vicinity of. The sectoral wage shares, and, also behave independently of each other. Therefore, the characteristic equation of (35) is simply given as

(36)

The characteristic roots are as follows.

(37)

Therefore, when is positive and is lesser than one, all the characteristic roots are negative and the equilibrium is a stable node, if and only if holds. In this case, the trajectory of is to converge to asymptotically. For the case where holds, the second characteristic root has a positive sign and the equilibrium is a saddle point. In this case, approaches to one, and moves toward zero and gradually dominates the movement of the trajectory. From the above analysis, we have the following proposition.

Proposition 1.

If and are satisfied, there exists a stable equilibrium. In the vicinity of the equilibrium, the wage shares of both sectors approach one, and the growth rate of the economy converges to .

The two broken lines in Figure 2 reflect the typical trajectories in the vicinity of. Any in the vicinity approaches on the horizontal plane, and moves along the corresponding trajectory of in the three dimensional space toward. As approaches, the velocity to the equilibrium gradually falls to zero. Therefore, the system needs an infinitely long time to converge on the equilibrium.

Let us consider the behavior of other variables in the vicinity. Let be in (32). Then:

(38)

Therefore,

(39)

This means that increases at the rate of. As and takes a constant value on the equilibrium path, the real wage rate also increases at the same rate,. Differentiating the aggregate share of wage with respect to time, we have

(40)

because the wage share is fixed at one at the equilibrium. Therefore, grows at the rate of. Differentiating with respect to time,

(41)

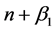
and we see that the capital/output ratio decreases. Since converges to the constant value, the capital/output ratio should infinitely approach zero as the profit share must be zero at. As a result, the economy produces only consumption goods and all of the products are distributed to workers. However, this does not necessarily mean that the capitalistic system vanishes on the way to, because the rate of profit remains positive over time¹⁷.

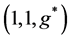
Case 2.

The stable equilibrium value of is and the Jacobian is as follows in this case.

(42)

The characteristic equation of (42) is

(43)

Therefore, the characteristic roots are

(44)

From the above conditions, we see that approaches one, if and hold. If is negative, approaches zero; otherwise it moves in the opposite direction, i.e., the system eventually converts to the case of. Following the same process as in the above case, we can confirm that grows at the rate of, and at. stays at a certain constant value.

In the final state of the economy that the trajectories approach toward, must hold and the aggregate wage share is 0.5, because the income generated in the investment goods sector is entirely distributed to the workers of the sector who spend all their wages on consumption goods, whereas all income generated in the consumption goods sector is entirely distributed to the capital owners of the sector who spend all their profits on investment goods. This can happen by infinitely increasing labor productivity in the consumption goods sector, or by a sufficiently high elasticity of factor substitution in the same sector such that workers are replaced with capital quite elastically. On the trajectories in the vicinity, rises at the rate of. This means that the workers in the consumption goods sector are constantly replaced with capital and this causes the wage share of this sector to shrink to zero.

Proposition 2.

If, and are satisfied, then there exists a stable equilibrium. In the vicinity of the equilibrium, the wage share of the investment goods sector approaches one, and that of the consumption goods sector approaches zero. The growth rate of the economy converges to. The aggregate share of wage income approaches 0.5.

Case 3. The other unstable cases

In the above cases, we examined only stable equilibria, but there also exist unstable trajectories that have no convergence point. For these cases, since any dynamic path of should stay in the compact quadratic space and the system has no complex characteristic roots, the trajectories must diverge to infinity along the g-axis. The two broken lines in Figure 3 represent typical trajectories around ¹⁸, when is greater than one and that of is lesser than one. Such a case can also be observed at, if the elasticities of factor substitution in both sectors are greater than one. We ignore these cases in the next section for the numerical simulations.

From the above three cases, we have the following proposition.

Proposition 3.

If the system has no inner equilibrium, and and, then there exist two possible corner equilibria, and. Since one of these two equilibria is a stable node and the other one is a saddle point, the system has only one stable equilibrium. If and, the system has no equilibrium and diverges to infinity.

5. Numerical Simulation: Validity of Piketty’s Proposition

We convert the differential system given by (9), (10), and (11) to the corresponding difference system by the fourth-order Runge-Kutta method with to see the

dynamic behavior of the system when it is not on the steady growth path¹⁹. As for the initial values of, and, they must be subject to the market clearing condition²⁰. To determine the initial equilibrium conditions, we assume that the CES production functions with constant returns to scale at are as follows²¹.

(45)

where, , and for and 2.

The two variables that are given the time derivatives explicitly in the original system, and, are historically given at the beginning of every period and determines, because the causality condition, which states that should be a monotonic function of so that the inverse function exists, is satisfied in Uzawa’s two-sector model²². The causality condition implies equilibrium in the factor markets and the profit maximization of firms. The other variables are then determined at their equilibrium values by the following three equations. The last one assures equilibrium in the goods markets.

(46)

(47)

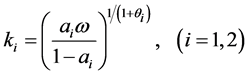
Therefore, there are five parameters,. Since holds, and are determined by the elasticities of factor substitution in each sector, to which we give some values in each simulation below. Therefore, we have three degrees of freedom to determine, and, and it is possible to arbitrarily choose their initial values, implicitly assuming a specific set of parameters of the production functions²³. We set at 0.7, at 0.75, and at 0.1 in the simulations below²⁴. We also suppose that to exclude any case where.

We set the growth rate of the labor force at 1.0%, which is presumably close to the average annual rate of population growth in the majority of developed countries. For the parameters of technological progress, we assume, according to the finding of Pol Antràs, that the rates of labor-augmenting technological progress of both sectors exceed the rates of capital-augmenting technological progress²⁵. We also assume, and as annual rates. Therefore, we equate six periods in the simulations to one year.

Case 1.

The results for the main variables are summarized in Panel 1(a), where “time’’ represents of a year. In the upper-right chart of the panel, the wage share, , consistently increases and eventually converges to one, and the aggregate elasticity of factor substitution remains lesser than one²⁶. It is also interesting that the wage share increases while the capital/output ratio (the inverse of) increases during the first 915 periods―almost 150 years―along with the decreases in the growth rate of income, ²⁷. This is caused by the relatively high initial value of for which the equilibrium value is 0.041. Therefore, the system must decelerate the rate of capital growth toward the equilibrium value. The negative effect of decreases in on the profit share exceeds the positive effect of increases in, and the wage share increases. Although we are discussing a process on the non-steady growth path, this result is at odds with Piketty’s argument that the wage share tends to rise when the economy slows down and (the capital/ output ratio in Piketty’s terminology) increases.

Piketty’s argument includes the comparative statics of the steady state in addition to analyses of the dynamic process. Since our system has no inner steady state, we have to rely on the comparative dynamics, which compares one particular trajectory with some other trajectories. Panel 1(b) shows the result of our comparative dynamics. We assume two economies, both of which share the same set of parameters except for the growth rate of the labor force

In this case, is set at either 0.01 or 0.005²⁸. A smaller value of increases the relative scarcity of workers to capital, and increases the marginal productivity of labor. This causes the wage rate to increase faster than the profit rate. This is reflected the upward shift of the growth rate of the ratio of factor prices in the lower-left chart in the panel. Since the elasticities of factor substitution in both sectors are lesser than one, the wage share increases as the result of the faster increase in regardless of the increase in the capital/output ratio caused by the decrease in the growth rate of income. This opposes the prediction forwarded by Piketty’s theory.

Panel 1(c) is the outcome from a comparative dynamics with two different initial values of, 0.05 and 0.025, and s are set at the equilibrium value at the initial period. These two economies have the same technological conditions, but they seem to be totally different economies. The economy with the lower rate of capital growth can be seen as a developed country, where both the capital/output ratio and the factor price ratio are high²⁹. Because of capital deepening, the marginal productivity of capital is low,

(a)

(b)

(c)

Panel 1. (a) Simulated Trajectories toward; (b) Comparative Dynamics for; (c) Comparative Dynamics for.

whereas that of labor is high, and this causes a high wage share. The other economy exhibits typical properties of developing countries. Capital is accumulating much faster than that of the other economy, and therefore, the profit rate is high, whereas the wage share is low to generate enough savings to finance such a faster capital accumulation. Therefore, this kind of comparative dynamics must be interpreted as a comparison between two different economies, and it is better not to take the result as what could be observed in a single economy. In any case, the result of this case also contradicts Piketty’s theory.

Figure 4 is the phase-diagram in the quadratic space of, where four trajectories start from different initial values³⁰. The trajectories cover a wide range of the domain, and the system exhibits its global stability. All of the trajectories converge to. We examined only the local stability in the above section, but the system also exhibits globally stable properties. In this case, all trajectories tend to converge on the right-upper corner equilibrium as the effects of initial conditions become weaker over time, and the wage shares of both sectors constantly increase in the long-run.

Although the final state is unrealistic, it is possible to suppose that the economy would approach such a state over hundreds of years. Therefore, it is arguable that such

an economy shows a steady upward trend of the wage share in the long run, and if this is the case, it is difficult to explain the recent incorrigible declines of the labor share in many countries as long-run phenomena. Rather, these declines should be considered as an ephemeral transit phase in terms of the economic process. Therefore, some institutional explanation, such as retrenchment in a welfare state and/or globalization of the economies³¹, might offer a better explanation.

Case 2.

Panel 2(a) is a typical outcome of the simulation with the same parameter values and initial conditions as case 1 barring the elasticity of factor substitution of the consumption goods sector: is 1.2 in this case. As shown in the panel, the trajectories are relatively stable in this case too. The growth rate of capital, , and the growth rate of income, , approach the steady growth rate of. We do not present the behavior of relative prices here, but our numerical experiment shows that the growth rate of the real wage rate approaches 0.04, which is equal to the growth rate of the labor productivity of the investment goods sector³².

In our simulation, the economy must constantly decrease the rate of capital accumulation. Therefore, a temporary excess supply of investment goods always appears and the price of investment goods falls so that the market equilibrium is maintained. This

(a)

(b)

Panel 2. (a) Simulated Trajectories toward; (b) Comparative Dynamics for.

decline of the price of investment goods means a rise in the real wage rate in terms of investment goods. Consequently, the firms of this sector reduce the number of workers and replace some of them with capital. Since the elasticity of factor substitution of this sector is less than one, the production of investment goods decreases, and the wage share in this sector increases. However, since the elasticity of factor substitution in the consumption goods sector is greater than one, the wage share of this sector decreases as firms employ more workers. The total effect of this process is a decline in the aggregate wage share.

The wage share decreases toward a fixed value―0.5 in this case―which implies that the aggregate elasticity of factor substitution tends to be nearly one in the long-run. In other words, the Cobb―Douglas function is an appropriate form of the aggregate production function in the long run, whereas each sector has a CES-type function³³. This holds good for any cases with a stable equilibrium.

In the two charts of Panel 2(a), and are constantly decreasing. Accordingly, the wage share decreases and the aggregate elasticity of factor substitution stays consistently in the upper area of the horizontal line at one for the entire period. So far, our results here conform to Piketty’s argument.

Let us look into the results of the comparative dynamics for this case, which is summarized in Panel 2(b). We set at two different values―0.01 and 0.005―again in this case. Owing to a decrease in the growth rate of the labor force, the trajectory of the income growth rate shifts downward as shown in the upper-right chart of the panel. In addition, in this case, the labor force is relatively scarce and rises more rapidly. This accelerates factor substitution from labor to capital and rises. Since the elasticity of factor substitution in the consumption goods sector is greater than one, the decrease in the wage share of this sector outweighs that of the investment sector and the aggregate wage share falls slightly.

If we increase the value of from 1.2 to 1.6, which Piketty believes is a plausible estimation of the actual rate of substitution, the slope of the curve in the upper-left chart of Panel 2(b) becomes steeper, but the gap between the two curves is widened only slightly. The gap of the wage share after 200 years changes only from 0.001 points for the case of to 0.002 points for the case of. This subtle difference is caused by the fact that both economies must slow down in accordance with a change in the growth rate of the labor force from 0.01 to 0.005. Therefore, since a higher profit share means a higher growth rate of capital, the economy should not increase the profit share excessively to keep the markets in equilibrium. Such a minor difference as in this case, is practically negligible. Therefore, the result obtained here barely conforms to Piketty’s argument³⁴.

Figure 5 is the phase-diagram in the quadratic space of, where four trajec-

tories start from different initial values. The trajectories cover a wide range of the domain, and the system exhibits its globally stable property in this case as well. All of the trajectories converge on the lower-right corner equilibrium. The elasticity of the investment goods sector is less than one, and the wage share of this sector increases constantly over time, whereas the elasticity of substitution of the consumption goods sector is greater than one and the wage share of this sector constantly decreases.

It should be noted here that the aggregate income distribution is remarkably stable for a considerable length of time as we have seen in the first case above. The wage share needs about 200 years in case 2 to decrease from 0.737 to 0.697 as shown in the upper-right chart of Panel 2(a)³⁵. It is less than the per annum³⁶. Therefore, it can be argued that the widely recognized stability of the functional distribution is theoretically observable even when the economy is not on the steady growth path.

Case 3. The saddle point

Panel 3(a) summarizes a simulated result for another set of parameters, where all parameter values are the same as in case 1, except for the rate of labor-augmenting technological progress in both sectors to analyze a saddle case: is here set at 0.01 and at 0.04. The equilibrium is a saddle point at and a stable node at for this case. The trajectory eventually approaches to.

As indicated in the panel, the aggregate elasticity of factor substitution, , is lesser than one in the initial phase and passes over the horizontal line at one from below around the 2510th period. This is reflected in the behavior of the wage share shown in the upper-right chart. It reaches to the maximum value at almost the same period and starts to decrease toward 0.5. This case shows that the aggregate elasticity can be greater than one for a long time, even if the elasticities of individual industries are lesser than one³⁷. However, it should converge to one eventually, because the wage share approaches the fixed value. This is because the aggregate elasticity of factor substitution is just another expression of the behavior of the aggregate income shares, and it is meaningless to say that either one of them causes the other³⁸.

As shown in the lower-right chart of Panel 3(b), the capital/output ratio rises steadily. However, the wage share rises until around the 2510th period. This is caused by rapid decreases in the rate of profit, because the initial rate of capital growth of 0.1 is much higher than the steady state level of 0.02, and the economy must distribute more income to workers to lower the rate of capital growth. The volume effect does not outweigh the price effect in this situation.

This result contradicts Piketty’s inference³⁹. There can be a case where his proposition derived from the assumption of the steady state economy contradicts the dynamic behavior of the economy that is not on the steady growth path, especially when its growth rate slows down. If such a situation continues for a considerable length of time in the real world, like more than 400 years in this case, his theory loses explanatory power. After this early stage, the trajectories in Panel 3(a) are consistent with Piketty’s theory, although that can happen only in the very distant future⁴⁰.

As for the comparative dynamics of this case, the trajectory of the wage share with the lower growth rate of labor force is consistently higher than that of the other case with the faster growth rate as shown in the upper-left chart of the Panel 3(b). This is because the elasticities of both sectors are lesser than one and a faster rate of increase in the ratio of factor prices are favorable to workers. The result of the comparative dynamics for the case 2 also contradicts Piketty’s theory.

Figure 6 is the two dimensional phase-diagram for this case⁴¹ that depicts the trajec-

(a)(b)Panel 3. (a) Simulated trajectories of the saddle Case; (b) Comparative dynamics for.

tories approach in the early stage, but is a saddle point and the trajectories turn toward eventually. A case like this is often ignored as merely an “unstable case’’ in dynamic analyses except in the literature on the dynamic optimal growth models, but these trajectories exhibit interesting behaviors as shown in Panel 3(a) and Panel 3(b). Therefore, such a behavior deserves to be paid much attention for a more precise understanding of the dynamic behavior of the economy that does not have any inner steady growth path.

Case 4. The inner equilibrium

Panel 4 shows the case where the system has an inner equilibrium so it can be compared with the other three cases. In this case, we assume and, and the system has an inner equilibrium at. The aggregate wage share converges to 0.624, and the aggregate elasticity of factor substitution to one. Although we do not show the results of comparative dynamics for, they are essentially the same as those for case 1.

As observed in the upper chart of the panel, it takes a long time for the system to reach the vicinity of the inner equilibrium. For example, starting from 0.516, the wage share needs about 850 years to increase by 0.1 points and reach 0.616. During such a long period, other institutional and/or political factors are far more important to explain the trend of income distribution than the purely economic process.

Figure 7 shows four trajectories with different initial conditions for the first 1200 periods. In this case, it is necessary to calculate the equilibrium values of and explicitly for each case to let all trajectories be generated exactly from the

Panel 4. Simulated trajectories toward the steady state.

same production functions. We set, and for this case. Any equilibrium initial point of should be given somewhere on the equilibrium locus in the lower-right diagram of Panel 4.

We set four different values on to determine the four sets of equilibrium initial conditions. As shown in Figure 7, the trajectories converge to the steady state very slowly, and the residual effects of differences among the initial conditions are still significant even after 1200 periods. This implies that changes in the initial conditions might have substantial effects on the current distribution of income.

6. Discussion

These results of our simulation are summarized in the table below, and Piketty’s argument appears to be verified in some cases. However, since the results of numerical simulations are generally affected by the relative magnitudes of the parameters, we should not derive any decisive conclusion from our limited numerical experiments. Most importantly, the location of the initial state relative to the equilibrium point is crucial, especially in the case of the saddle point.

The remarkable stability of aggregate income distribution over time was distinctly observed in our simulations. This is true, even when the corner equilibrium is a saddle point or when the system has no inner equilibrium. This stability is mainly brought about by the mechanism of factor substitution. If the capital/output ratio stays at the same level when the growth rate and the profit rate fall, then the profit share decreases. However, a decrease in the profit rate causes the ratio of factor prices to be increased. This causes more of the labor force to be replaced with capital and the capital/output ratio to increase. Therefore, the effect of a decrease in the profit rate on income distribution is partly offset by the increase in the capital/output ratio. In the case where the aggregate elasticity of factor substitution is one, this mechanism works perfectly, and the aggregate income distribution naturally stays at the same level. The sectoral composition of outputs also contributes to the stability of income distribution through an adjustment of relative prices in the case of multi-sector models.

Therefore, we may argue that it is difficult to explain a major change in the trend of income distribution as a purely economic process. Rather, the standard neoclassical theory verifies the robust stability of income distribution regardless of the existence or non-existence of the inner steady state. This result also suggests that the stylized stability of income distribution can be explained without assuming a Cobb―Douglas type production function and/or Harrod-neutral technological progress even in the long run. In contrast, external shocks that reset the initial conditions, such a change in the tax regime, might have far more important effects on the trend of income distribution⁴².

7. Conclusions

The most crucial point of our analysis in this paper is to determine the case that offers the most appropriate description of the real economy. As Robert Rowthorn notes in his

critical paper on Piketty’s work ( [28] ), there are numerous studies that estimate the aggregate elasticities of factor substitution to be significantly lesser than one. This is also true of studies on individual industries. For example, Pol Antràs reports that the elasticity of substitution is likely to be considerably below one under biased technological change ( [20] ), and Robert Chirinko and Debdulal Mallick estimate that the aggregate elasticity is only 0.406 for the U.S. ( [29] ). In addition, as Antràs found, labor-aug- menting technology grew faster than capital-augmenting technology. If we rely on their estimations, then our model suggests that case 1 is the most probable, and the wage share must demonstrate a steady upward trend over time. Although the aggregate elasticity of factor substitution can be greater than one even when the elasticities of the individual industries are lesser than one, our model proves that such an economy generally tends to converge to the state where all incomes are distributed to workers as long as the stability condition is satisfied. For workers in such a state, “when the storm is long past, the ocean is flat again’’ ( [30] , p. 65). Consequently, Piketty’s diagnosis about recent economic inequality is, as far as the functional distribution is concerned, at odds with the theoretical explanation of Uzawa’s type of the neoclassical growth theory.

Therefore, if the recent incorrigible declines of wage shares in many countries should not be considered as short-run phenomena, we should pay more attention to institutional and/or political aspects of the problem than to the technological factors. In this regard, Piketty’s theory is better understood as a theory based on historical data and not one deducible from standard neoclassical growth theory, and his second fundamental law, which plays a crucially important role in his theoretical explanation, can be taken as a “bridge’’ that we, economists, cross for historical and socioeconomic studies on the subject. In this sense, the conclusion of the present paper endorses his statement that “The history of the distribution of wealth has always been deeply political, and it cannot be reduced to purely economic mechanism’’ ( [2] , p. 20).

However, our results are obtained solely by using Uzawa’s two-sector model with the classical savings function as well as by using limited numerical simulations. Further investigations with a more general framework and numerical simulations with various settings of the parameters are indispensable to confirm our conclusions.

Acknowledgements

The author expresses his grateful appreciation to Takehiro Nagaoka for helpful suggestions on the numerical simulation in the present paper.

Cite this paper

Morita, M. (2016) Non-Neutral Technological Progress and In- come Distribution―Piketty’s Fundamental Laws in a Neoclassical Two-Sector Model. Theoretical Economics Letters, 6, 1267-1298. http://dx.doi.org/10.4236/tel.2016.66119

References

Appendix: Derivation of (9)-(11)

Since we assume the production functions are homogenous of degree one,

(A.1)

where,. and. Using (A.1), we have the ratio of factor prices, which we denote as:

(A.2)

From (1)-(5), and (A.1),

(A.3)

where. Substituting this into (A.2), we have

(A.4)

Differentiating this equation by time, , we have the following equation.

(A.5)

where. Substituting this equation into (15), and solving it with respect to,

(A.6)

Next, differentiating (A.4) by,

(A.7)

Since, substituting this into the above equation, we have,

(A.8)

Substituting (A.6) into (A.8), we have

(A.9)

Differentiating the wage shares by, we have

(A.10)

Substituting (A.6) and (A.9) into this equation, we have the next equation as follows.

(A.11)

Substituting into the above equation, we have (9) and (10).

Next, differentiating by,

(A.12)

Substituting (15) and

into (A.12), we have,

(A.13)

Substituting (A.6) and (A.9) into (A.13), we have

Substituting and into this equation, we have (11).

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact tel@scirp.org

NOTES

¹ [1] .

² [2] .

³ [3] , p. 30.

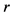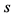⁴Piketty’s first fundamental law is a definition of the aggregate profit share;, where is the rate of return on capital and is the capita/income ratio. His second fundamental law, which states that, where is the savings rate and 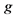is the steady growth rate of income, can be derived from the condition of the steady state. When the economy is in a steady state, 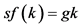holds, where 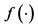is the production function and is the capital/labor ratio. This is nothing other than the second law.

⁵ [4] , p. 52.

⁶In an interview, Piketty states more precisely that “the real world is better described by a multidimensional capital model, where at the same time we have a real estate sector, energy sector, many different sectors with different capital intensities” ( [5] ). See also Section 3.3 of [6] , where they refer to the relative price of capital and consumption goods.

⁷ [8] , p. 4. The empirical study reported in [9] reached the same conclusion.

⁸By “inner equilibrium,” we mean a steady state where the wage shares of all production sectors in the economy are positive but less than one.

⁹In this regard, Jones states that “the theoretical analysis behind Piketty’s prediction of rising wealth inequality often includes a key simplification in the relationships between variables: for example assuming that changes in the growth rate 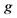will not be mirrored by changes in the rate of return, or that the saving rate net of depreciation won’t change over time. If these theoretical simplifications do not hold ... then the predictions of a rising concentration of wealth are mitigated” ( [3] , p. 45).

¹⁰“Asymptotic trajectory” means a growth path continuously sifted by non-neutral technological progress over time, toward which the actual trajectories gravitate.

¹¹If we extend our bibliographic scope to models with agents’ intertemporal optimization, there are a number of papers―such as by [15] [16] and [17] , to name a few contemporary examples―that analyze the effect of technological progress in a multi-sector model. However, these studies are based on the assumption of maximizing behavior of the representative consumer who takes all products of the economy as wages and profits; even undistributed corporate savings ultimately belong to him/her. Although their investigations offer very interesting insights, inequality in functional income distribution does not seem to cause any social problem within such a framework, because such an inequality would be the consequence of his/her behavior that optimizes intertemporal allocation of lifetime’s personal income. Piketty himself refers explicitly to this point. See [2] , p. 581, note 18.

¹²With the classical savings function, we do not have to deal with the problem posed by [18] . If we assume that savings come from wage income, then, we must include the capital income of workers in the model, which would make our analysis far more complex.

¹³Although corporate savings are only a part of profits, the classical saving function implies that corporate savings will increase as the wage share decreases when firms preserve a part of their profits as internal savings, and this is empirically corroborated in [17] .

¹⁴We include only reproducible physical capital in K.

¹⁵See the Appendix for their derivation procedure.

¹⁶The right-hand side of (12) can be zero, but we exclude any possibility for and satisfying such a specific relationship.

¹⁷This result should be slightly modified if we take depreciation of capital into account. In that case, the economy must produce some investment goods for the replacement, and the profit share must take a certain positive value to keep the gross savings positive.

¹⁸For these cases, is zero only at the point where, because the dynamic behavior of is given by when is in the vicinity of or.

¹⁹At least qualitatively, different values of do not alter the result.

²⁰We abbreviate the time argument “(0)” for simplicity of the expressions below.

²¹At, the parameters of technological progress do not appear in the production functions.

²²See [1] .

²³Since and determine the value of, is positive and lesser than one for any determined by and arbitrarily chosen values of and.

²⁴We assume to determine the equilibrium value of, because we do not give the initial value of explicitly.

²⁵He found that “labor-augmenting efficiency grew about 3% faster than capital-augmenting efficiency” in the U.S. private sector. See [20] , p. 25.

²⁶According to Robert Lawrence, many empirical studies report that labor-augmenting technological progress is relatively rapid and that the aggregate rate of factor substitution is much lower than one ( [21] ).

²⁷Since represents the growth rate of capital, which is always equal to the rate of profit under the assumption of the classical savings function, we use to represent henceforth. However, Piketty defines as the steady state value, whereas here, is the actual value.

²⁸The parameters of technological progress are alternatives for comparative dynamics, but some of them disturb the stability condition.

²⁹In this case, the factor price ratio of the economy with the growth rate of 0.05 is one, whereas that of the other economy with the growth rate of 0.025 is 3.6759023.

³⁰We set the initial conditions arbitrarily in the phase-diagram, and this implies that we give a different parameter set to the production function for each case.

³¹See [22] [23] and [24] .

³²If we take the nominal wage rate as the numeraire, a rise in the real wage rate implies that the price of consumption goods rises faster than that of investment goods. [17] reached the same conclusion by using the comparative statics of steady states, which was that the lower price of investment goods explains roughly half of the decline in the labor share.

³³This has also been empirically corroborated. For example, Tipper reports, “The data suggest a Cobb― Douglas form of the constant elasticity production function is appropriate at the aggregate level in New Zealand in the long run. At the industry-level, the evidence suggests a constant elasticity production function with varying elasticities across industries is appropriate” ( [25] , p. 31).

³⁴We will not state any result of comparative dynamics for differences in the initial conditions because the outcomes of those simulations are, at least qualitatively, the same as those of Panel 1(c) except for.

³⁵This decreasing rate is far lower than the statistical estimations for several countries. According to Angel Estrada and Eva Valdeolivas, the labor share of the U.S. fell from 64.24% in 1980 to 59.79% in 2010. If this decreasing rate continues, the labor share will decrease to 14.8 points in 100 years. See [26] , p. 13.

³⁶Even if we set at a very high step-resolution, say, the wage share after 20,000 periods―equiva- lent to 200 years―starting from the first period is still. Therefore, the step-resolution does not matter greatly to our conclusion.

³⁷Since) holds in our model, is affected by the sectoral composition of the output. Therefore, becomes greater than one regardless of the factor substitution of the individual sectors when the economy boosts the production of investment goods relatively to accelerate capital accumulation. In this case, holds after around the 2510th period, whereas for the entire period.

³⁸The aggregate elasticity of substitution should be one at the steady state, because the income shares are fixed there. In this sense, it is difficult to understand why Piketty estimates the elasticity of substitution around 1.3 - 1.6, whereas he employs comparative statics of the steady state. See [2] , p. 221.

³⁹See [2] , p. 221. Although the shapes of these trajectories greatly depend on the values set for the initial conditions, their qualitative property is maintained.

⁴⁰If we set at a value greater than one in this case, then the corner equilibrium of becomes a saddle point and the simulation result is completely reversed.

⁴¹Since we set the initial conditions arbitrarily, each trajectory has a different production function. Moreover, since we curtail the -axis in the figure, the trajectories may intersect with each other at some points in the quadratic space.

⁴²See also [27] .