Theoretical Economics Letters
Vol.06 No.05(2016), Article ID:70508,10 pages
10.4236/tel.2016.65093
Empirical Reserve Price in Forestry: Application to US Forest Service
Francis Didier Tatoutchoup
École des Hautes Études Publiques (HEP), Université de Moncton, Moncton, Canada

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 25, 2016; Accepted: September 9, 2016; Published: September 12, 2016
ABSTRACT
This article exploits data from ascending auctions from the US Forest Service to estimate an optimal reservation price in forestry when prices are uncertain and when the forest owner endogenizes the cutting age of trees. The results suggest that there is a huge gain in terms of the forest owner profit to use the estimated optimal reservation price rather the well-known reservation price proposed by Laffont and Maskin’s and Riley and Samuelson’s which is suboptimal in the forestry context. Finally, the results also confirm that the reservation price set by the US government agency is too low.
Keywords:
Reserve Price, Auctions, Estimation, Forestry, Autoregressive Process

1. Introduction
In forestry, auction mechanism is commonly used to sale trees. For example, the US government agency, the United States Forest Service (USFS) uses auctions for the sale of standing timber. Optimal auction often involved the setting of an optimal reserva- tion price to maximize the forest owner’s surplus. Over the past decades, empirical works have derived the reservation in forestry under various assumptions using the well known result of [1] [2] . However, in a recent theoretical paper, [3] showed that this result is not suitable for the forest management problem to estimate an optimal reservation in forestry because it ignores the harvesting decision. Therefore, he proposed an optimal reservation price that endogenizes the harvesting decision by assuming that bidders’ valuations depend on the optimal harvest time of trees namely, the optimal rotation which is the central problem in the management of forest resources. Following [3] , this article aims to estimate an optimal reservation in forestry when stumpage price are uncertain and then to analyse to what extent the result differs from that of [1] [2] in term of the forest owner’s profit.
This is not the first article to derive empirically an estimate of the optimal reserve price in auctions. In a pioneering work, [4] used data from the Forest Service of British Columbia to derive the optimal reserve price in ascending auctions. Later [5] derived a semi-parametric estimator of the optimal reserve price in the first price sealed-bid auctions, and [6] derived an estimate of the optimal reservation price under affiliated private value in ascending auction. All of these papers assumed the stumpage market price to be deterministic; they also ignored the forest management problem. This article estimates the optimal reservation price by assuming that bidders’ valuations are inde- pendent and identically distributed (the IPV paradigm) in order to tackle the forest management problem. It contributes empirically to the literature of forest auctions by extending the results of Laffont and Maskin as well as Riley and Samuelson in the con- text of forestry management.
The article is organized as follows. Section 2 presents the theoretical model. Section 3 provides an empirical application of the model to the US Forest Service (USFS). The econometric specification of the model, the identification, and the estimation of para- meters, as well as the calculation of the optimal reservation price and its implications are discussed. Finally, Section 4 concludes the paper.
2. The Model
In this paper, I consider the bidding behavior in an ascending auction. Following [3] , I assume that there are N potentials risk neutral firms that compete at each period t for the possession of an homogeneous stand of trees of same age 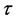 which is the time interval between planting and harvesting. Let
which is the time interval between planting and harvesting. Let 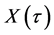 denote the total volume of timber to be harvested. I will focus on symmetric equilibria with increasing bids. At period t, firms
denote the total volume of timber to be harvested. I will focus on symmetric equilibria with increasing bids. At period t, firms 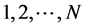 submit bids
submit bids  that depend on their average cost (the exploiting cost per unit of timber harvested) according to a decreasing function
that depend on their average cost (the exploiting cost per unit of timber harvested) according to a decreasing function  so that
so that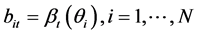 . The random variable
. The random variable  is the private information of firm
is the private information of firm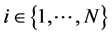 . Assume that each
. Assume that each 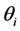 is drawn independently from the same distribution with the cumulative distribution function
is drawn independently from the same distribution with the cumulative distribution function 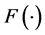 and the density function
and the density function 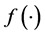 on the interval
on the interval . The valuation per unit of volume of timber of firm i at period t is given by:
. The valuation per unit of volume of timber of firm i at period t is given by: 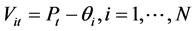 where
where 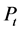 is the stumpage price of the timber which is assumed to follow an
is the stumpage price of the timber which is assumed to follow an  (autoregressive process of order q) process that is stationary and described by
(autoregressive process of order q) process that is stationary and described by
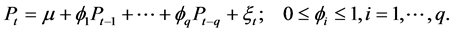 (1)
(1)
The stochastic term 



It is shown in [3] that the expected revenue from auction in period t is
where

The problem of the forest owner is to choose the optimal rotation age 







The solution of the problem will be compared with that provided by [1] [2] which satisfies Equation (5) below.

3. Econometric Specification and Estimation
To estimate the optimal reservation price, I will use a structural model by estimating respectively the distribution function of the costs 


3.1. Timber Auction Data
To compute an estimate of the optimal reserve price, I use auctions data provided by the USFS, a US government agency that manages public forests and organizes the sale of standing timber. The sales are conducted using either first price sealed-bid auctions or ascending auctions2. Each auction involves the selling of trees in a specific track. A track of forest may consist of trees of different species. When there is more than one species, the reserve price is set for each species. However, the transaction bid depends on the total amount bid for all species. This raises an additional difficulty for the computation of the optimal reserve price that must take into account the allocation of the total amount among species as such information is not available. Therefore, I restrict my attention to auctions with only one species. I focus on auctions organized from 1973 through 1993. I selected two representative species namely, Douglas fir and Lodgepole pine among 71 species sold during these periods. This choice stemmed three reasons. First, both species represent one-third (33.79%) of the total volume of timber sold during the considered period. Second, in terms of the volume of trade, they represent 10.7% of the total number of sales during the considered period, with 5.9% for the Douglas fir and 4.8% for the Lodgepole pine. Finally, the availability of data for a homogeneous stand is a factor. The data come from the six regions of the western half of the United States, labelled as 1 through 6, and consist of 1532 sales that received at least two bids3. Finally, after cleaning the data and removing missing data, 1304 data remained of which 1094 in ascending auctions. These 1094 auctions will be used for estimation. This sample data consists of 754 for Douglas fir and and 340 for Lodgepole pine. Table 1 summarises the statistics of variables in the sample of auctions studied. All dollar figures are converted to constant 1982 dollars per MBF (thousand board-feet) of timber.
Table 1 shows that, in terms of the quality of timber, Douglas fir is more valuable than Lodgepole pine as the stumpage price of Douglas fir is approximately six times higher than that of Lodgepole pine.
3.2. Estimation
To estimate the distribution of costs, I follow [4] by assuming that the distribution of cost follows a Weibull distribution with scale 





Table 1. Summary statistics.
L refers to the total.

In each lth auction, the standing timber is characterized by a vector of variables
The estimation of parameters of the distribution functions is summarized in Table 2. Before interpreting the estimate parameters that are statistically significant, let’s highlight that bids are increasing in the scale parameter (


Before going on to calibrate the optimal reservation price, I first model the diffusion process of the stumpage prices using Equation (1). Table 3 shows that both Douglas fir and Lodgepole pine follow a first-order autoregressive model that is stationary around a deterministic trend (constant term)6. Observations include annual data from 1950
Table 2. Estimation results.
Table 3. Autoregressive models.

through 2005 for Douglas fir and from 1965 to 2010 for Lodgepole pine7. Prices are in constant 1982 dollars per MBF. Price series are from the USFS Department of United States of Agriculture ( [13] ) and from [14] .
Finally, I rely on the yield tables of Douglas fir and Lodgepole pine for the estimates of growth functions (for the yield table of Douglas fir, see [15] [16] ; for the yield table for managed stands of Lodgepole pine, see [17] ). Because it is more convenient to work with continuous formula, I assumed the following exponential growth function specified as

3.3. Calibration Results
Using Equation (3)-(5) with preceding estimates, I calculated the model optimal reservation price (Model), Laffont and Maskin’s and Riley and Samuelson’s reservation price (LMRS) used in previous empirical studies, and the reservation price set by the USFS for Lodgepole pine and Douglas fir, respectively, when the interest is 3%. The results are summarized in Table 4. For Lodgepole pine and Douglas fir, the optimal reservation price is on average 91% and 117.9% respectively, higher than that set by the USFS. Table 4 also confirms the theoretical results of [3] that the model optimal reserve price derived is higher than that of LMRS. The difference in percentage for Lodgepole pine and Douglas fir is on average 13.1% and 10.9% respectively.
I also quantified the gain of the forest owner by using the model optimal reservation price rather than reservation price of LMRS. The results are summarized in Table 5, which shows the profits per acre and the gains in percentage by using the optimal reservation price rather the LMRS reservation price8. The gain in moving from a LMRS
Table 4. Reserve Prices, r = 3%.
Table 5. Expected profits, r = 3%.
reservation price to the model optimal reservation is considerable. For Douglas fir, it is on average equals 7770$ per acre, or 10%. That gives an average total gain of 1,081,350.9$ (the average number of acres of Douglas fir is 139.17). For Lodgepole pine, the gain derived from moving from LMRS to the optimal contract is 18.2%. This represent a gain of 487,461.48$ (the average number of acres is 620.18). The results obtained when the interest rate is 3% are corroborated with the results summarized in Table 6, showing the expected gains when using the model reservation price rather than the LMRS for additional interest rates of 4% and 5%. For example, when the interest rate is 5%, the gain is 9.2% for Douglas fir and 53.2% for Lodgepole pine.
4. Conclusion
This article combined auctions and the forest management problem to estimate the optimal reservation price in forestry when prices are uncertain and follow an auto- regressive model. Exploiting data in ascending auctions provided by the USFS, I esti- mated the optimal reserve price for the selling of the Douglas fir and Lodgepole pine which are two representative species traded by the USFS. Both stumpage prices follow a first order autoregressive process that is stationary around a drift term. First, the opti- mal reservation price is 91% and 31.5% for Lodgepole pine and Douglas fir respectively higher than the reserve price set by the USFS thereby confirming what is well accepted among economists namely, that the reservation price set by the US government agency is too low. Second, compared to Laffont and Maskin’s and Riley and Samuelson’s re- servation price used in previous studies, the optimal reservation price is on average 13.1% and 10.9% higher respectively, for Lodgepole pine and Douglas fir. Finally, there is a considerable gain in expected profit up to 53.2% and 10.0% respectively, for Lodgepole pine and Douglas-fir indicating that the forest owner should use the opti- mal reservation price that take into account the harvesting decision derived by Tato- utchoup ( [3] ) rather than Laffont and Maskin’s and Riley and Samuelson’s reservation price.
Table 6. Average expected profits and interest rate.
Acknowledgements
We thank the Editor and the referee for their comments.
Cite this paper
Tatoutchoup, F.D. (2016) Empirical Reserve Price in Forestry: Application to US Forest Service. Theoretical Economics Letters, 6, 897-906. http://dx.doi.org/10.4236/tel.2016.65093
References
- 1. Laffont, J.J. and Maskin, E. (1980) Optimal Reservation Price in the Vickrey Auction. Economics Letters, 6, 309-313.
http://dx.doi.org/10.1016/0165-1765(80)90002-6 - 2. Riley, J.G. and Samuelson, W.F. (1981) Optimal Auctions. The American Economic Review, 71, 381-392.
- 3. Tatoutchoup, F.D. (2016) Theoretical Reserve Price in Forestry. Theoretical Economics Letters, 6, 761-767.
http://dx.doi.org/10.4236/tel.2016.64080 - 4. Paarsch, H.J. (1997) Deriving an Estimate of the Optimal Reserve Price: An Application to British Columbia Timbers Sale. Journal of Econometrics, 78, 333-357.
http://dx.doi.org/10.1016/S0304-4076(97)80016-4 - 5. Li, T. and Perrigne, I. (2003) Timber Sale Auctions with Random Reserve Prices. Review of Economics and Statistics, 85, 189-200.
- 6. Aradillas-Lopez, A., Gandhi, A. and Quint, D. (2013) Identification and Inference in Ascending Auctions with Correlated Private Values. Econometrica, 81, 489-534.
http://dx.doi.org/10.3982/ECTA9431 - 7. Baldwin, L. (1995) Risk Averse Bidders at Oral Ascending-Bid Forest Service Timber Sales. Working Paper, RAND Corporation.
- 8. Baldwin, L., Marshall, L.R. and Richard, J.F. (1997) Bidder Collusion at Forest Service Timber Sales. Journal of Political Economy, 105, 657-699.
http://dx.doi.org/10.1086/262089 - 9. Athey, S. and Levin, J. (2001) Information and Competition in U.S. Forest Service Timber Auctions. Journal of Political Economy, 109, 375-417.
http://dx.doi.org/10.1086/319558 - 10. Haile, P. (2001) Auctions with Resale Markets: An Application to U.S. Forest Service Timber Sales. American Economic Review, 91, 399-427.
http://dx.doi.org/10.1257/aer.91.3.399 - 11. Haile, P. and Tamer, E. (2003) Inference with an Incomplete Model of English Auctions. Journal of Political Economy, 111, 1-51.
http://dx.doi.org/10.1086/344801 - 12. Athey, S., Levin, S.J. and Seira, E. (2011) Comparing Open and Sealed Bid Auctions: Evidence from Timber Auctions. The Quarterly Journal of Economics, 126, 207-257.
http://dx.doi.org/10.1093/qje/qjq001 - 13. United States Department of Agriculture, Forest Service. Pacific Northwest Research Station, General Technical Report PNW-GTR-857, 2011.
- 14. Ulrich, A.H. (1988) U.S. Timber Production, Trade, Consumption and Price Statistics. 1950-86. USDA For. Serv. Misc. Publ. No. 1460. 81.
- 15. McCArdle, R. (1949) The Yield of Douglas-Fir in the Pacific Northwest. USDA Tech. Bull. No. 201.
- 16. United States Department of Agriculture (1929) Volume, Yield, and Stand Tables for Second Growth Southern Pines. USDA Misc. Publ. No. 50.
- 17. Myers and Clifford, A. (1920) Rocky Mountain Forest and Range Experiment Station. Fort Collins, Colo. Published 1967.
- 18. Athey, S. and Haile, P. (2002) Identification of Standard Auction Models. Econometrica, 70, 2107-2140.
http://dx.doi.org/10.1111/1468-0262.00371
Appendix
Estimation in Ascending Auctions
9


The observation in the ascending auction is












Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
1The reservation price ,
, 


2For detailed descriptions of different auctions and contracts between the USFS and the loggers and contractors, see [7] - [11] .
3A total of 2085 sales satisfy all my criteria; however, I dropped 553 sales, representing 26.52% of the initial sample, that received less than two bids.
4



5Additional estimation of 
6I use both Dickey-Fuller and Phillips Perron stationary tests. The null assumption of a unit root is rejected at the 5% level.
7The fact that stumpage prices go beyond 1993 is not problematic when the price process is stationary, as it is the case in this article. Just the length of data is relevant; starting time and ending time are not important.
8Because the planting cost is too small compared to the total revenue, I have assumed that it is zero.







