Theoretical Economics Letters
Vol.05 No.06(2015), Article ID:61831,5 pages
10.4236/tel.2015.56084
Ramsey’s Belief and the Plausibility of Keynesian Economics
Masayuki Otaki
The Institute of Social Sciences, University of Tokyo, Tokyo, Japan

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 16 November 2015; accepted 7 December 2015; published 10 December 2015

ABSTRACT
Using Ramsey’s formulation of the probability theory, this study considers the plausibility of alternative monetary theories―Keynesian and monetarism, which is defined by the people’s confidence in such theories. It is naturally assumed that the more complicated theory entails a dearer cost to understand. Keynesian equilibrium is supported only through belief in the stable intrinsic value of money. Conversely, monetarism requires that laypeople have special and difficult knowledge so as to be confident about its assertion; namely, the linear relationship between nominal money supply and price; the actual value of Marshallian k and the volume of nominal money supply. As such, the Keynesian belief is far more prevalent in the actual economy.
Keywords:
Ramsey’s Belief, Keynesian Economics, Monetarism, Plausibility, Equilibrium Selection

1. Introduction
Not only the familiar probability theory, which is established by Kolmogrov relying on the measure theory, but also Ramsey’s [1] theory depends on the frequency theory of probability. The measure theoretic approach is ultimately meaningless without the law of large numbers (i.e. ergodic property) because the exact shapes of the density function and/or cumulative distribution function are unknowable.
Ramsey discards the law of large numbers because everyday samples are usually small in size. Instead, he constructs his theory by relying only on the subjective mathematical expectation, which, of course, does not relate to the law of large numbers at all. The subjective probability, p, is defined the ratio of the subjectively expected number of occurrences, m, from the total number of incidences, n. That is,
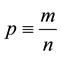 . (1)
. (1)
The most prominent feature of his theory is that he connects the subjective probability with one’s action towards the proposition in question. He assumes that one can know whether the proposition is right if one pays some investigation cost,  , where d denotes the difficulty of knowing the true causality. In addition, he also assumes that whenever one acts in accordance with the belief that the proposition in question is true, his expected subjective gain from such behavior must be equal to the gain obtained by knowing the truth. Unless such a relationship upholds, he surely ceases to act charted by the belief (i.e. subjective probability), and instead, ascertains the true causality at the cost
, where d denotes the difficulty of knowing the true causality. In addition, he also assumes that whenever one acts in accordance with the belief that the proposition in question is true, his expected subjective gain from such behavior must be equal to the gain obtained by knowing the truth. Unless such a relationship upholds, he surely ceases to act charted by the belief (i.e. subjective probability), and instead, ascertains the true causality at the cost 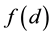 when having decided on the action. It is natural to assume that f is an increase function of d.
when having decided on the action. It is natural to assume that f is an increase function of d.
Let the benefit obtained when the proposition is true be denoted as a and as b when it is false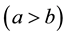 . The subjectively expected gain from the n times trials,
. The subjectively expected gain from the n times trials,  , is
, is
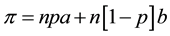 . (2)
. (2)
If one, otherwise, accesses the true causality in each trial, gain,  , becomes
, becomes
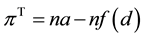 . (3)
. (3)
It is assumed that Equation (2) is equalized to (3); then, taking Equation (1) into consideration, we obtain the subjective probability (i.e. the belief on the validity of the proposition), p, as
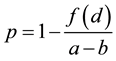 . (4)
. (4)
Equation (4) implies a serious meaning. Along with an increase in the difficulty of understanding and checking the proposition in question, individuals become less confident to it. The reason is that the more complex the proposition becomes, the more costs are incurred for examining its truthfulness. Such kind of tendency is quite prevalent in everyday life.
In relation to economic theory, there is acute difference on the difficultness necessary for understanding between Keynesian theory and monetarism. As Otaki ([3] and [4] ) shows, Keynesian theory upholds when people merely believe that the value of money, which is defined by the inverse of the price index, is not affected by a change in nominal money supply. In other words, as long as people rationally believe the intrinsic value of money, money becomes non-neutral.
In contrast to such a simple structure of Keynesian economics, as Otaki [4] shows, monetarism requires much information and complex processing to understand and believe it; every individual is incessantly concerned about the movement of nominal money supply and all must investigate whether the price level increases proportionately to nominal money supply; and they all must exactly know the value of Marshallian k. To summarize, the value, d, of monetarism can be deemed to be much larger than that of the Keynesian thesis.
This implies that, ceteris paribus, Keynesian economics becomes more confident among laypeople than monetarism. As such, if people behave in accordance with their confidence in a theory, the economy in reality becomes to possess the properties of Keynesian economics.
The rest of this paper is organized as follows. Section 2 constructs a model based on Otaki [2] [3] , and [4] with Ramsey’s [1] concept of belief and shows the plausibility of Keynesian economics being superior to monetarism. Section 3 is the brief concluding remarks.
2. Plausibility of Keynesian Economics
2.1. Two Alternative Models
A two-period overlapping-generations model with infinite time horizon is considered, as in Otaki [2] and [4] . There is no population growth and every individual has an identical utility function:
 , (5)
, (5)
where 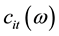 is the consumption level of good
is the consumption level of good 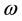 of an individual, who is born at the beginning of period t, during his i-th stage of life.
of an individual, who is born at the beginning of period t, during his i-th stage of life. 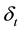 is a definition function the value of which takes unity when the individual is employed and zero when unemployed.
is a definition function the value of which takes unity when the individual is employed and zero when unemployed. 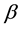 is the disutility of labor supply.
is the disutility of labor supply.
For simplicity, it is assumed that the marginal productivity of labor is unity and that there is no fixed cost. All firms are price takers, and thus, earned profits become zero in equilibrium. In addition, this model assumes that the labor market is in interior equilibrium where some individuals are always unemployed, and the equilibrium nominal wage stacks at the nominal reservation wage. These assumptions yield the following equation:
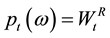 , (6)
, (6)
where 



Combining Equations (6) and (7), the equilibrium inflation rate, 



where 

where 
Equation (9) is the real total expenditure of the old generation, 

and hence the monetary authority keeps the real money supply constant. That is, the growth rate of money is fixed at
Equation (9) contains two undetermined endogenous variables; real GDP


On the other hand, when people believe that the value of money is not absolute but relative, the monetarist assertion to close the model is summarized by the following equilibrium price function:

One must note both resulting equilibria are self-fulfilling. From Equations (10) and (11), it is clear that the equilibrium GDP earned under Keynesian proposition, 





2.2. Ramsey’s Belief and Keynesian Economics
This subsection applies the Ramsey’s formula (4) to examine which of the two above mentioned macroeconomic theses is plausible. Before undertaking the analysis, one must clarify what kind of knowledge is needed for a layperson in economics to understand each theory.
1) For the Keynesian theory, the layperson must be able to confirm that the current price level, 
2) For monetarism a) the layperson must be able to confirm that the current price level changes proportionately with the nominal supply as in Equation (11), b) he must be conversant with the linear function to understand the relationship in a), and c) he must know the value of the proportional constant 

As such, it is evident that the monetarist thesis is far more difficult and laborious to understand than the Keynesian theory. Accordingly the value of d in Equation (4) is thought to be much larger in the case of monetarism.
In addition, whenever the true proposition is the Keynesian thesis, it is assumed that the subjective distribution when the proposition is false is uniform within the interval
in Equation (4), is
tion of such proposition being false is uniform within

Hence, the denominators in Equation (4) are the same value independent of whether the true proposition is Keynesian or monetarism2. This implies, therefore, that the belief in Keynesian thesis, 

3. Concluding Remarks
This study develops the concept of plausibility in alternative monetary theories with the key concept being Ramsey’s [1] belief. While Keynesian economics is upheld only by the belief in the stable value of money in terms of goods, monetarism is not sustained until laypeople in economics understand not only the exact linear relationship between the nominal money supply and the price index but also macroeconomic statistics with which they are almost unconcerned in everyday life. Consequently, the cost for knowing the truth is much cheaper in the Keynesian thesis. This implies that Keynesian economics is more plausible than monetarism although both theories possess the self-fulfilling property. In this sense, Ramsey’s theory can be regarded as an effective equilibrium selection procedure.
Acknowledgements
The author is grateful for the incisive comments of reviewers, and he also appreciates Professor Susumu Cato and Doctor Masaoki Tamura for encouraging discussion. The basic research of this paper is funded by MEXT/ JSPS KAKENHI Grant Number 60183761.
Cite this paper
MasayukiOtaki, (2015) Ramsey’s Belief and the Plausibility of Keynesian Economics. Theoretical Economics Letters,05,725-729. doi: 10.4236/tel.2015.56084
References
- 1. Ramsey, F.P. (1926) Truth and Probability. In: Mellor, D.H., Ed., Philosophical Papers, Cambridge University Press, Cambridge, 52-109.
- 2. Otaki, M. (2007) The Dynamically Extended Keynesian Cross and the Welfare-Improving Fiscal Policy. Economics Letters, 96, 23-29. http://dx.doi.org/10.1016/j.econlet.2006.12.005
- 3. Otaki, M. (2011) A Pure Theory of Aggregate Price Determination. Theoretical Economics Letters, 1, 122-128. http://dx.doi.org/10.4236/tel.2011.13026
- 4. Otaki, M. (2015) Keynesian Economics and Price Theory: Re-Orientation of a Theory of Monetary Economics. Springer, Tokyo. http://dx.doi.org/10.1007/978-4-431-55345-8
- 5. Keynes, J.M. (1933) Essays in Biography. In the Collected Writings of John Maynard Keynes, Vol. 10, Cambridge University Press, Cambridge.
NOTES
1Note that knowing the resulting benefits empirically does not necessarily mean that all individuals are informed of the whole structure of the economy.
2Note that there is no economic surplus in this simplified setting. However, as Otaki [2] and [4] shows, if the equilibrium concept of goods markets is interchanged with monopolistic competition instead of perfect competition, there emerges an economic surplus that is proportional to the real GDP.
3Ramsey [1] proves the existence of more general type of belief based on an axiomatic approach, which includes the availed belief in this paper as a special case. In this sense, there is a certain limit in this paper. Ramsey [1] begins with defining the proposition the probability of which is 1/2. Subsequently, by using the assumption of some kind of rationality, he succeeds in achieving to allot the degree of belief to all general propositions. About the rationality, he denotes
“I propose to take as a basis a general psychological theory, which is now universally discarded, but nevertheless comes. I think fairly close to the truth in the sort of cases with which we are most concerned. I mean the theory that we act in the way so that a person’s actions are completely determined by his desire and opinions.” (p. 69)
This is quite akin to the concept of the economic rationality despite his aversion to utilitarianism. In addition, it is necessary for more fruitful analysis on the concept of plausibility to explore how human cognition progresses. In my model, this problem closely connects with how we should determine the value of d, although I still remain in assuming that d is an increasing function of the number of knowledge.
Keynes [5] prophets
“Thus he [Ramsey] was led to consider `human logic’ as distinguished from ‘formal logic’. Formal logic is concerned with nothing but the rules of consistent thought. But in addition to this we have certain ‘useful mental habits’ for handling the material with which we are supplied by our perceptions and by our memory and perhaps in other way, and so arriving at or towards truth; and the analysis of such habit is also a sort of logic. The application of these ideas to the logic of probability is very fruitful.” (p. 338)




