Received 23 July 2014; revised 20 August 2014; accepted 15 September 2014

ABSTRACT

Industrial development in Japan is accompanied by massive migration from agricultural to industrial areas. In a modified Harrod-Domar model, this paper compares two steady states, the first and the second, which emerge before and after the termination of such migration, respectively. Then, the paper shows that employment rates must be lower in the second steady state. Further, by examining the effects of fiscal policy, the paper shows that the balanced budget multiplier exceeds unity, and fiscal policy raises households’ disposable income and consumption.

Keywords:

Industrial Development, Migration, Employment

1. Introduction

As indicated in Figure 1, massive migration from agricultural to industrial areas terminates in the early 1970s in Japan. This termination of migration coincides with the end of that country’s rapid economic growth. Unemployment rates also increase after the termination of migration. The first aim of this paper is to provide a simple framework that is consistent with these phenomena.

The framework that we present is a modified Harrod-Domar model. Although this model might be regarded as an elementary framework in old textbooks, this paper demonstrates that it still gives insights into dynamic economies. In his seminal paper, Harrod [1] argues that the warranted growth rate does not coincide with the natural rate of growth¹. Even though the warranted rate exceeds the natural rate, an industrial economy can grow at the warranted rate so long as large numbers of migrants flow into the industrial areas. However, once this migration terminates, a discrepancy between the warranted rate and the natural rate inevitably emerges as an actual

disparity requiring resolution². The current paper suggests that in these circumstances, a fall in the employment rate may play a central role in adjusting the warranted rate of growth.

Using a model with fixed coefficients, Kaldor [2] proposes an adjustment mechanism through income distribution. He argues that the rate of savings is higher out of profits than out of wages; as a result, the average saving rate positively relates to the profit share in income. If the profit share moves adequately, the warranted rate becomes equal to the natural rate through a change in the average savings rate. The adjustment mechanism proposed by the current paper is similar to Kaldor’s to the extent that the savings rate is variable. However, profit share is constant in our model. We emphasize that the consumption of individual households is not proportional to their income. Accordingly, the average savings rate of the whole economy decreases with a fall in income per household, which depends on the employment rate. Thus, a fall in employment rate can reduce the savings rate, and thereby adjust the warranted rate to the natural rate.

The second aim of the paper is to investigate the multiplier effect of government spending in the circumstance of underemployment. Ono [3] provides a clear explanation of the balanced budget multiplier, which is unity in the short run. Our comparative statics show that the balanced budget multiplier exceeds unity, and accordingly, government spending enhances households’ disposable income and consumption.

2. The Model

Let us consider a simple model consisting of two economies: an agricultural economy and an industrial economy. Suppose that each economy is self-sufficient and has no connection to the other except with regard to possible migration. Our focus is upon economic growth in the industrial economy where a market economy prevails. For the agricultural economy, we assume that local communities guarantee individual households a living standard that slightly exceeds the subsistence level. When jobs are available in the industrial economy and the wage rates are more satisfactory than the earnings in the agricultural economy, migration occurs from the agricultural to the industrial economy. We also assume that one household has 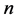successors in both economies; consequently, the total population grows at the gross rate of.

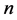2.1. Households in the Industrial Economy

Let us specify the behaviour of households living in the industrial economy. Each household lives for one period. A household indexed by 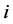maximizes the following utility:

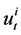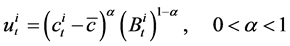
where 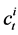denotes consumption at perio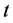d and 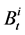denotes a transfer from household 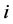to its successors. Constant 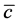reflects the minimum level of consumption. Each household is endowed with one unit of labor. In real terms, the budget constraint is given by

,

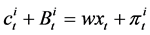where 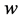denotes the real wage rate; 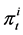denotes the asset income that is proportional to the share of own asset; 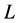denotes the number of households located in the industrial economy; and 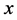denotes the employment

rate. When the quantity of employed labor is denoted by, the employment rate is given by ³.

As a result of maximization, the consumption becomes

, (1)

Note that owing to, individual consumption given by (1) is not proportional to income⁴.

2.2. Firms

Let us adopt a familiar monopolistic competition model. Industrial firm maximizes its profit

at period, subject to the demand function and the labor input function, where

denotes the price of good; the quantity of produced good; the nominal wage rate; the employed labor for producing good; the price index; the aggregate demand; and the labor input coefficient⁵. The firm uses capital, which is determined by investment at period. At period, therefore, the capital cost is regarded as a sunk-cost. As a result of profit maximization, the price of good

becomes. In a symmetric equilibrium, (and). Thus, we obtain the real

wage rate in the industrial economy:

(2)

where implies labor share in income⁶.

Furthermore, let us assume that investment is planned exactly for realizing the above profit, i.e.

, where v denotes the capital coefficient. It is assumed that capital depreciates completely in one

period.

Lastly, let us assume that firms distribute the whole profit to households, and therefore,

. (3)

3. First Steady State with Migration

Now, consider the first stage of industrial development, when an abundant supply of labor is available through migration from the agricultural economy. We assume that

(4)

Wage rate given by (2) is higher than reservation wage that is based on earnings in the agriculture

economy. Then, equilibrium employment rate would be determined by the well-known Har-

ris-Todaro mechanism⁷:

(5)

Taking (1), (3), and (5) into account, aggregate consumption is given by

(6)

Note that the aggregate consumption is proportional to aggregate income, while the individual consumption

given by (1) involves a positive constant.

Now, let us investigate the warranted rate of growth. The goods market equilibrium is given by. Then, using (6), we have

, (7)

where denotes the saving rate:. Then, from (7) and, we obtain the

warranted growth rate:

(8)

Following Harrod, let us assume that this warranted rate is higher than the natural rate of growth. Since we ignore technical progress, it implies that, i.e.,

(9)

Even if this inequality holds, the industrial economy can grow at the rate of as long as the inflow of migrants continues.

4. Second Steady State without Migration

Since, the industrial economy growing at the rate of will completely absorb agricultural labor sooner or later. After the agricultural economy disappears, the industrial economy can grow at the rate of in the long run. Now, let us examine how the warranted growth rate can be adjusted to natural rate.

Let denote the employment rate in the second steady state without migration. Aggregate consumption can be indicated by

(10)

Accordingly, the equilibrium output becomes

(11)

where. Then, from (11) and, the warranted rate of growth is

. However, the growth rate in the steady state is bound to be, and therefore it must hold that

. This means that has to be

(12)

Comparing (5) and (12) under condition (9), we obtain the following proposition.

Proposition 1: The employment rate in the second steady state is lower than the employment rate in the first steady state:.

This examination reveals that the warranted growth rate can be adjusted toward the natural growth rate by a

decrease in the employment rate. A fall in output raises consumption rate, and

thereby reduces the saving rate. Further, the fall in decreases employment. Hence, a particular employment rate exists under which. Note that there is a paradoxical aspect: the higher the growth rate of

population, the higher the employment rate:.

5. Fiscal Policy in the Second Steady State

Now we investigate how government spending affects macroeconomic performance. Let denote per capita government spending. Aggregate spending is given by, and the goods market equilibrium is indicated by. We examine a simple balanced budget policy, i.e. the government levies a lump-sum tax on each household. Then, instead of (10), aggregate consumption is

. (13)

Taking (13) into account, we can derive the following employment rate in the second steady state:

(14)

which means that government spending raises the employment rate through its demand-expansion effect.

Per capita output is given by

. (15)

Note that: the balanced budget multiplier exceeds unity. This is because

government spending enhances investment as well as consumption in the steady state. Defining per capita dis-

posable income as, we have. Thus, the following proposition is obtained.

Proposition 2: The balanced budget multiplier is greater than unity. Accordingly, government spending increases households’ disposable income and consumption.

6. Conclusion

By taking into account individual consumption that is not proportional to income, the current paper examines two steady states: one is characterized by a high employment rate accompanied by rapid economic growth with migration; the other is characterized by a lower employment rate accompanied by slower economic growth without migration⁸. Since insufficient demand for goods restricts the economy in the second steady state, it might not be surprising that Keynesian fiscal policy improves the situation. However, it would be worth noting that the balanced budget multiplier exceeds unity in the second steady state.

Acknowledgments

I wish to thank Makoto Mori, Hideki Nakamura, and Friday Seminar participants at Osaka City University for their valuable comments on an early version of this paper. I would like to thank an anonymous referee for his/her useful suggestions.

References

NOTES

¹The former is the rate that warrants the full utilization of capital, and the latter is the sum of the growth rates of the working population and labor productivity.

²Although one of Harrod’s points of emphasis is premised on the instability of warranted growth, the current paper focuses on another issue: the discrepancy between the warranted rate and the natural rate of growth. Domar’s [4] main interest seems to be in characterizing the warranted rate rather than the discrepancy between the warranted rate and the natural rate of growth.

³To simplify the analysis, we assume underemployment instead of unemployment.

⁴The transfer implies savings, and owing to, the saving function becomes convex with respect to income. Recently, Moav [5] , Galor and Moav [6] , and Nakajima and Nakamura [7] adopt similar saving functions.

⁵The derivation of the demand function is roughly explained as follows. Let denote the consumption index of household, which is given by. Then, from optimization, the demand for good, , is derived as, where. In a similar way, let denote the investment index of firm, which is given by. Then, the demand for good , is derived as. Aggregating these results, we obtain demand function. For instance, see Blanchard and Kiyotaki [8] .

⁶The level of nominal wages does not influence our arguments hereafter.

⁷See Harris and Todaro [9] .

⁸We only compare two steady states in which capital is fully utilized. The actual process of transition may include trial and error in investment. Then, excessive holdings of capital will occur temporarily. However, if a representative firm decides on investment with perfect foresight, the economy would quickly attain the second steady state.