ABSTRACT

We are interested in incentivizing experimental subjects to report their beliefs truthfully, without imposing assumptions on their risk preferences. We prove that if subjects are not risk neutral, it is not possible to elicit subjective probabilities or the mean of a subjective probability distribution truthfully using deterministic payments schemes, which are predominant in the literature. We present a simple randomization trick that transforms deterministic rewards into randomized rewards, such that agents with arbitrary risk preferences report as if they were risk neutral. Using this trick, we show how to elicit probabilities, means, medians, variances and covariances of the underlying distribution without assuming risk neutrality.

1. Introduction

The economic literature on the elicitation of an expert’s subjective beliefs has focused on so-called proper scoring rules. These mechanisms, which are used in many economic experiments, reward the expert on the basis of post-elicitation events such that it is in the expert’s interest to report her true beliefs if she is risk neutral. The quadratic scoring rule (QSR) [1] is the most popular rule, used to elicit the probability of an event or the mean of a random variable. In the absence of risk neutrality, there is an incentive to report conservative beliefs in order to avoid large losses [2]. This is a problem, since risk neutrality is shown to be widely violated in experimental studies [e.g. 3]. Indeed, Armantier and Treich [4] show experimentally that consistent with risk aversion, elicitation with the quadratic scoring rule leads to conservative bias in reported beliefs.

There are different ways to get around this problem. Offerman et al. [5] propose a way to correct for deviations of risk neutrality and expected utility, by quantifying the size of deviations for each individual. Alternatively, an earlier literature starting with Smith [6]¹ shows how one can induce risk neutrality by rewarding subjects using binary lottery tickets. This idea has been used to show how to elicit the subjective probability of an event [e.g. 10,11] in a way similar to the elicitation of a reservation price [12].

We extend this literature in several ways. First, we prove that deterministic schemes are not adequate if one does not know the risk preferences of the expert. Second, we combine the literature on scoring rules for risk neutral preferences with the literature on incentivizing with lottery tickets to show that one can elicit a median or any quantile without making assumptions on risk preferences. We also present an alternative way to elicit a probability or mean based on the randomized quadratic scoring rule. Third, we present a new deterministic rule, and its randomized counterpart, to elicit variances and covariances when two independent observations are available.

2. Preliminaries

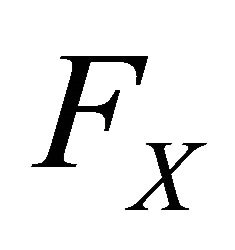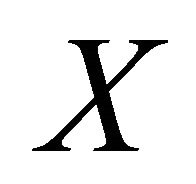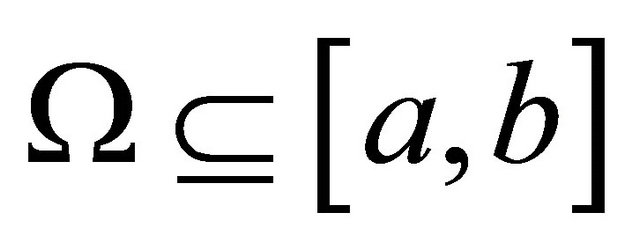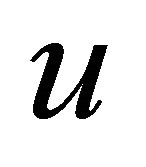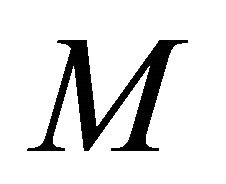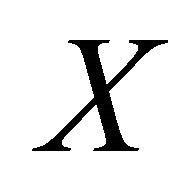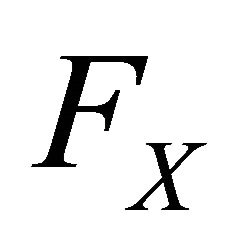We consider two people, an expert and an elicitor. The expert has subjective beliefs about the distribution of a bounded random variable that yields outcomes belonging to with. The expert maximizes expected utility for some utility function on such that for some. The elicitor only knows that yields outcomes belonging to, and would like to learn some parameter of the distribution. We consider the use of a reward system or scoring rule which rewards the expert on the basis of her report 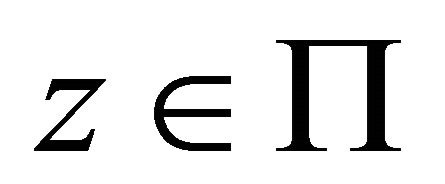and a single random realization of. Here, is a distribution over the rewards which includes a deterministic reward as a special case. In the literature, is called strictly proper for 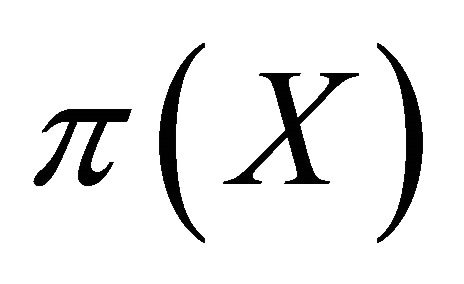if

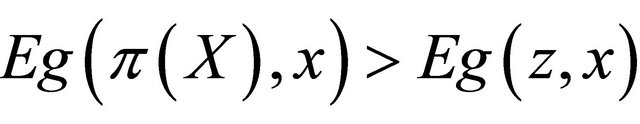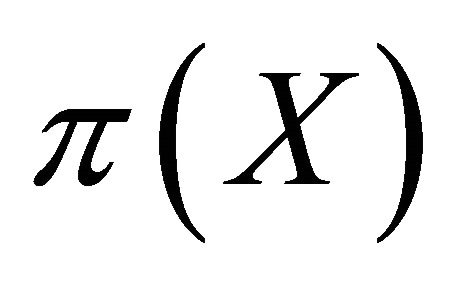for all. We say that a rule elicits if 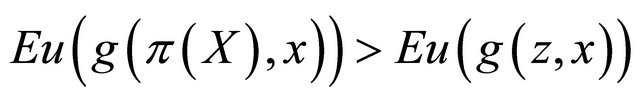for all 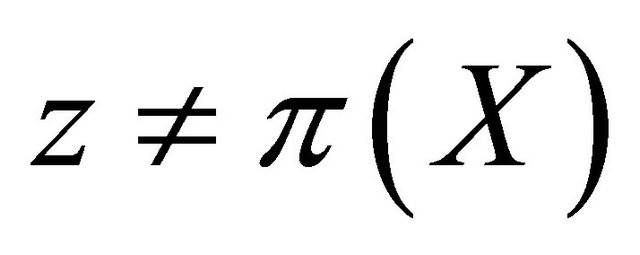and all with.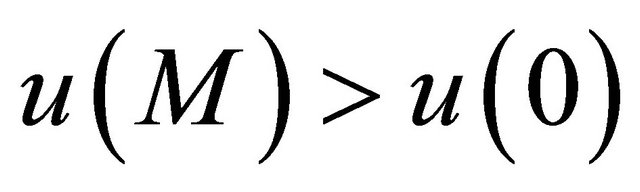

3. Limitations of Deterministic Rewards

Consider an elicitor who wishes either to learn about the mean of some random variable with support in, or about probability of some event. We obtain the following result.

Proposition 1. A scoring rule with a deterministic reward cannot elicit the probability or the mean.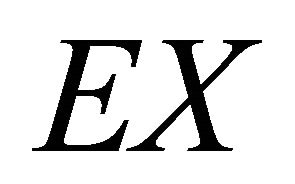

The proof is in the Appendix. The intuition is simple. The elicitor has only one parameter, the realization, to incentivize the expert to tell the truth. On the other hand, there are two dimensions of uncertainty as the elicitor does not know 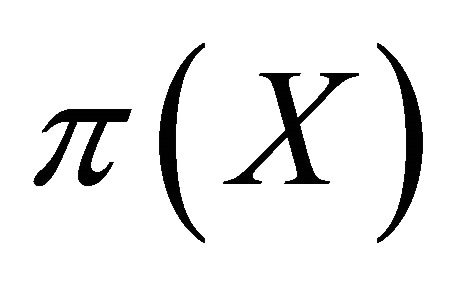and

4. Probabilistic Elicitation

We now consider elicitation using probabilistic or randomized reward functions. The idea, first elaborated by Smith [6], is that one pays the experts in lottery tickets rather than money. The size of the prize is given by the probability of winning the lottery. Hence where 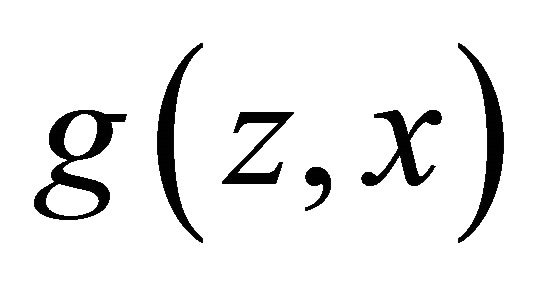is now the payoff distribution awarded conditional on. Using this idea, we show how to elicit probabilities, means, different quantiles, and variances and covariances.

4.1. Randomization Trick

We use the following “randomization trick” to transform deterministic into probabilistic payoffs. First, given a deterministic reward function, determine and

such that 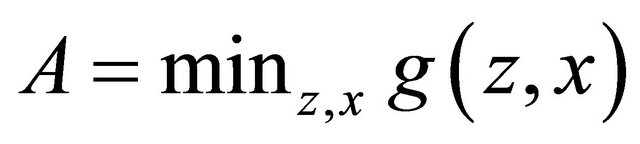and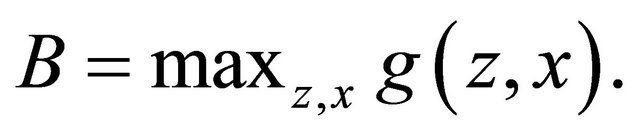

Second, draw a realization 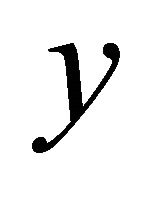from a uniform distribution on and then pay if and pay 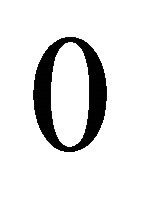if

Formally, we replace the deterministic reward 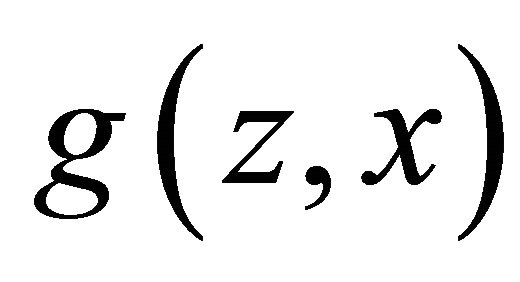by the randomized reward

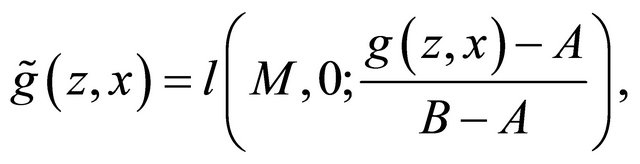
where 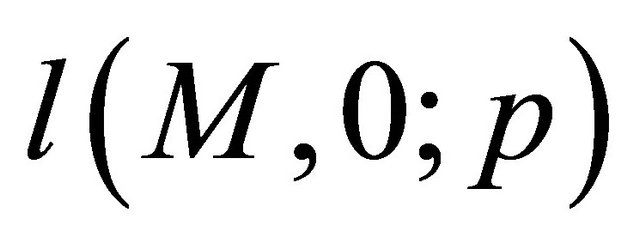is a lottery that pays 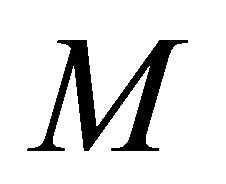with probality 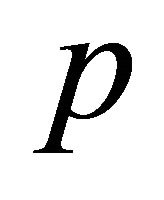and 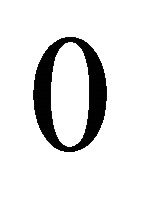with probability 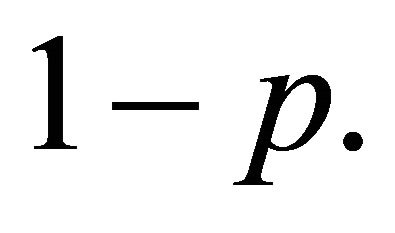Consequently,

The expected utility of the expert equals an affine transformation of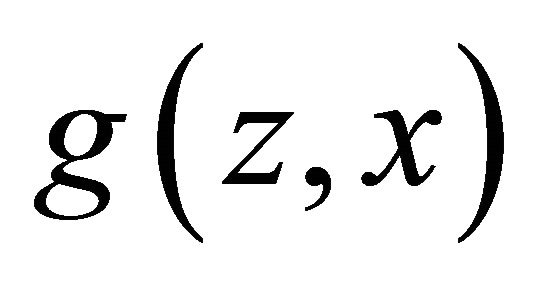. Thus, a report that maximizes her expected utility is a report that maximizes the utility of a risk neutral expert and vice versa. In particular, elicits iff 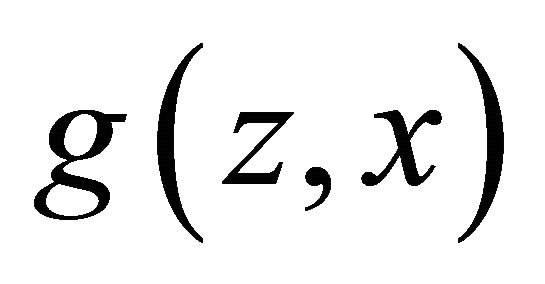is strictly proper for.²

4.2. Eliciting Probabilities

Randomized rewards for the elicitation of probabilities have received quite some attention. Grether [10] (see also Holt [15, ch. 30] and Karni [16]) presents a simple reward function where a prize is rewarded with some probability that depends on the draw of two uniformly distributed random variables. Allen [11] presents an alternative rule that relies on a draw of a random variable that has a more complex probability distribution. Mclvey and Page [17] uses a randomized version of the quadratic scoring rule in an experimental application, which is similar to the rule we present below.

The QSR (for the event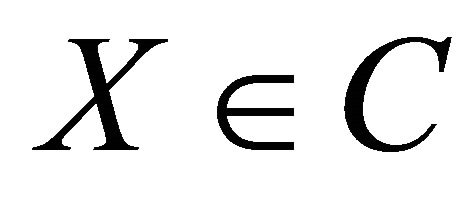) is given by

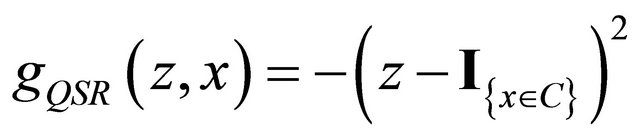
and is strictly proper for [1]. The randomized quadratic scoring rule (for the event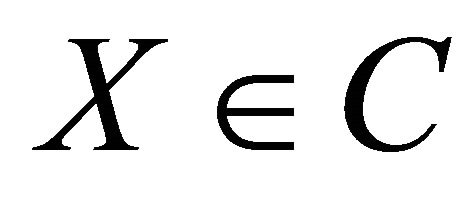), short rQSR, is defined by

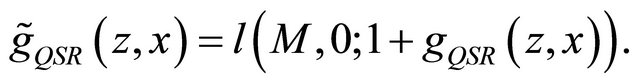The following result obtains:

Proposition 2. The randomized quadratic scoring rule elicits.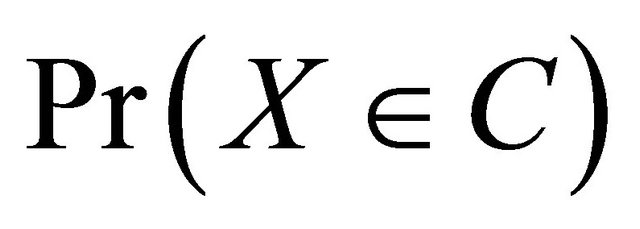

Note that the expected payoffs under rQSR are identical to those under the rules of Allen [11] and McKelvey and Page [17] when.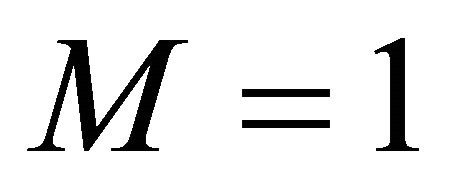

4.3. Eliciting the Mean

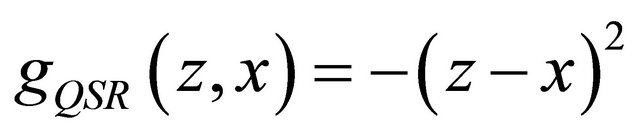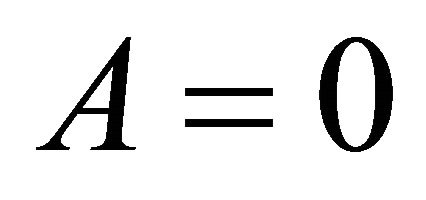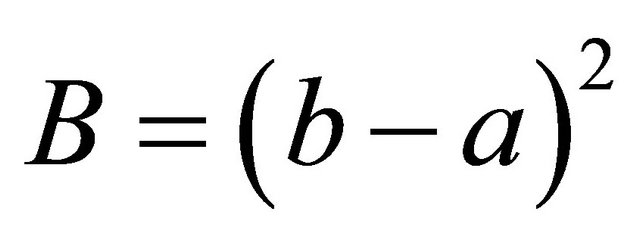To elicit the mean, we combine the randomization trick with the fact that the QSR is a strictly proper scoring rule for the mean (for risk neutral experts). Given and we obtain the randomized quadratic scoring rule as defined by

Proposition 3. The randomized quadratic scoring rule elicits.

4.4. Median and Quantiles

The quantile scoring rule, due to Cervera and Munoz [18] is a strictly proper scoring rule for the quantile 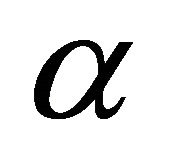of the distribution 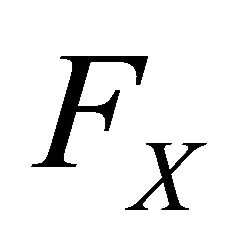of for any given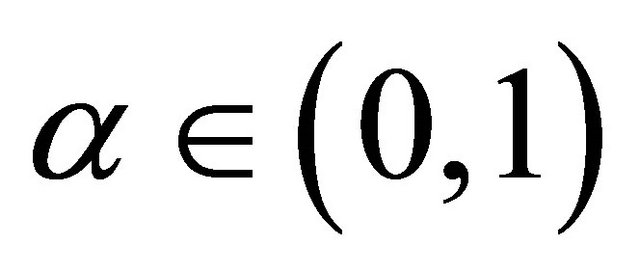. Its reward function is given by The randomized quantile scoring rule is hence given by 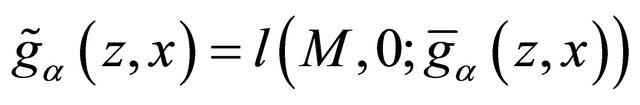where

Proposition 4. The randomized quantile scoring rule elicits the quantile.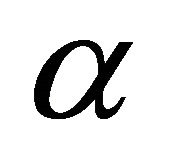

In particular, Proposition 4 shows how to elicit the median by setting.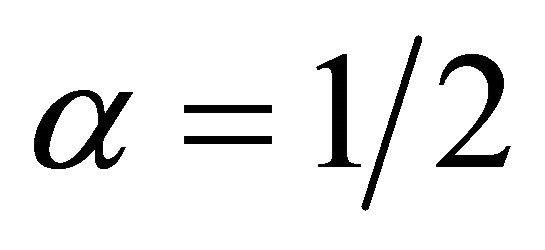

4.5. Variance and Covariance

In order to elicit the variance of we assume the elicitor can condition on two independent realizations 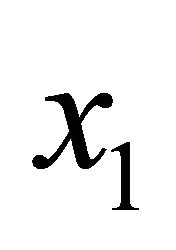and of 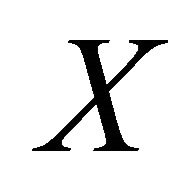when rewarding the expert. So we conder a reward function 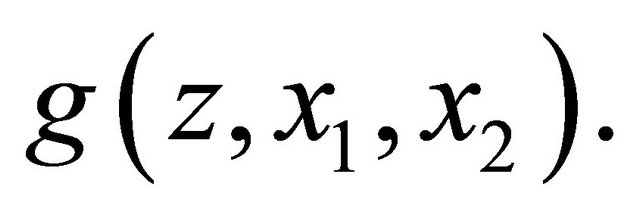We first construct a strictly proper scoring rule. Following Walsh (1962),

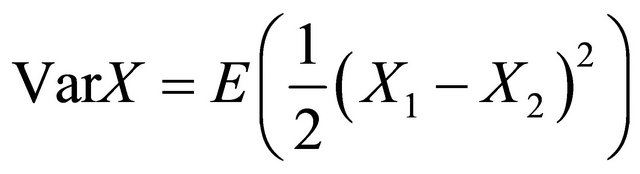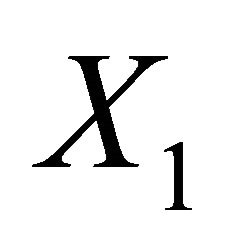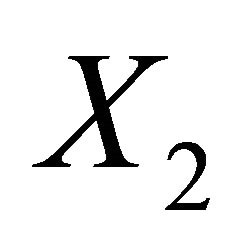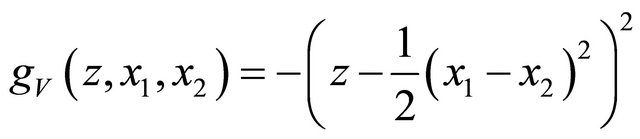where and are indendent copies of We combine this with the quadratic scoring rule to obtain that the variance scoring rule that is strictly proper for Given

we obtain the randomized variance scoring rule by

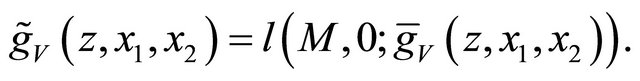
Proposition 5. The randomized variance scoring rule elicits the variance of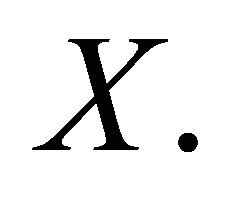

Similarly we can elicit the covariance given two ranm variables 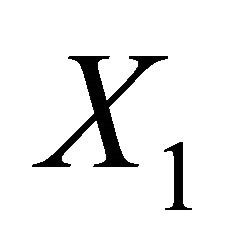and 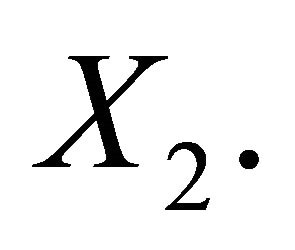We assume that

for 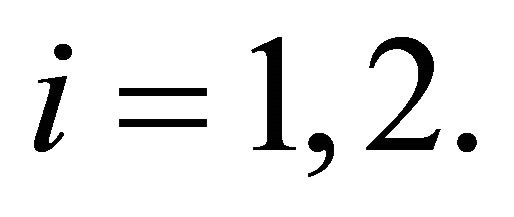Here we condition on a realization 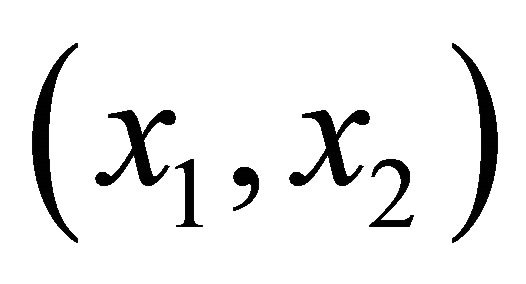drawn from 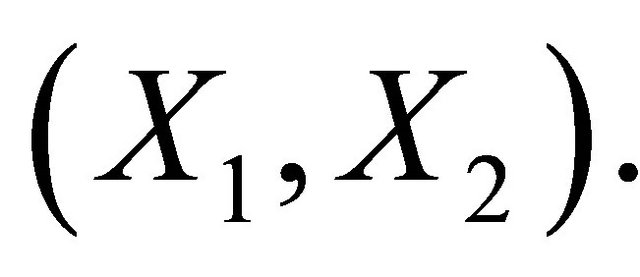Again following Walsh (1962)we use the fact that

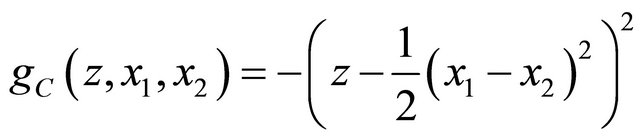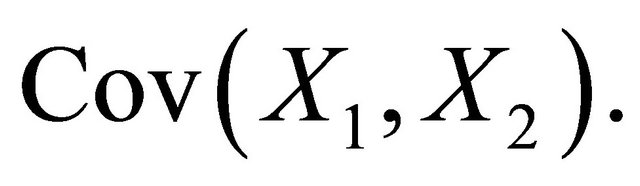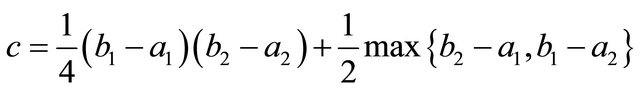and then use the QSR to define the covariance scoring rule that is strictly proper for Given and

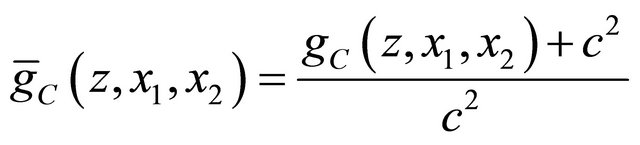
we obtain the randomized covariance scoring rule by

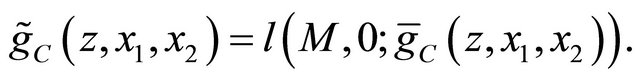
Proposition 6. The randomized covariance scoring rule elicits the covariance of and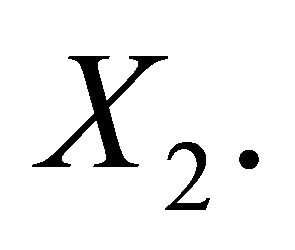

5. Conclusions

We have rigorously shown the limits of deterministic scoring rules for belief elicitation. To overcome those limitations, we applied the idea of paying in lottery tickets to transform known deterministic scoring rules for belief elicitation, such as the well-known QSR, into randomized rules. These rules provide agents with incentives to truthfully report parameters of a subjective probability distribution for all risk preferences, and can be used in experimental applications.

This paper has considered the theoretical side. On the empirical side, it is an open question whether these rules have the desired properties in actual applications, and how they are best presented to subjects. Selten et al. [19, see also review therein] raises doubt whether subjects rewarded using lotteries behave as if risk neutral in experiments. More recently, Harrison et al. [14,20], and Hossain and Okui [13] provide evidence that the produre can induce subjects to behave more in line with risk neutrality.

REFERENCES

Appendix

Proof of Proposition 1. If one can elicit the mean of a random variable for all distributions in then one can also elicit the probability of an event as 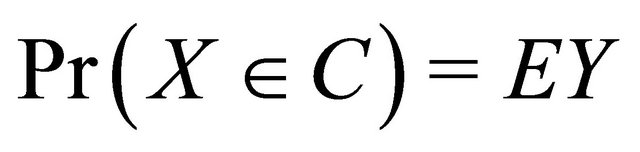if is the Bernoulli random variable such that 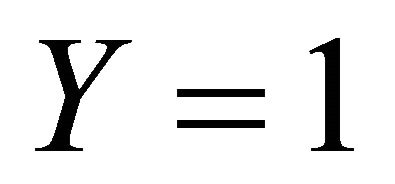if and only if Hence it is enough to show that one cannot elicit 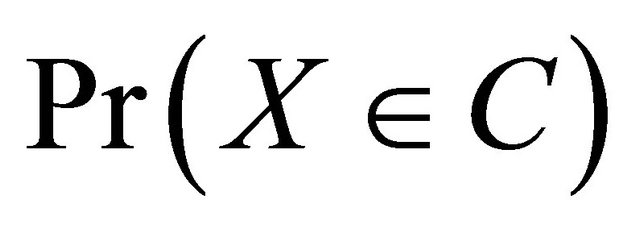to prove that one cannot elicit

We first show that 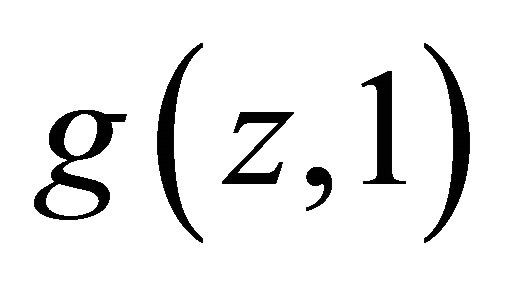and are differentiable almost everywhere. Once this is established the first order conditions reveal the impossibility.

Consider 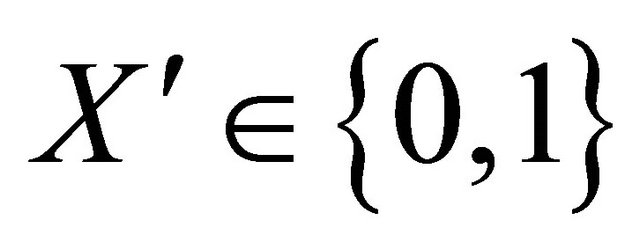where So

Let

Assume that elicits for all concave. Then we have for all

For 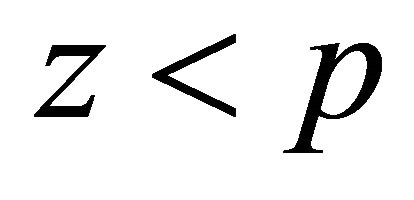and 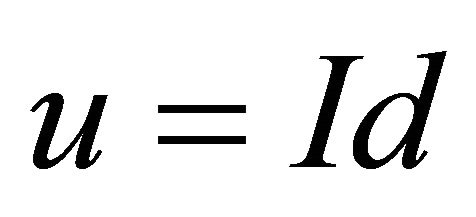we have

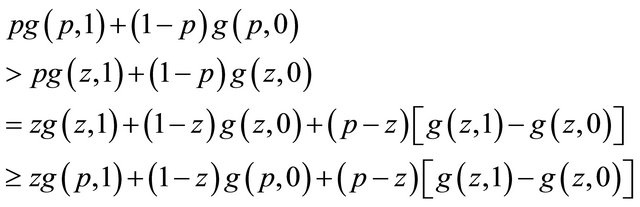
so

so

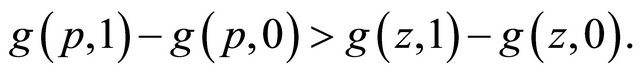
Hence we have shown that 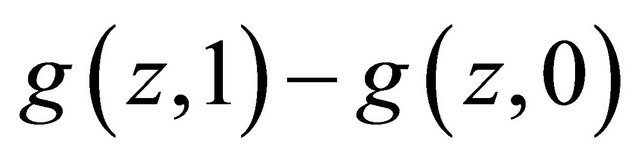is strictly increasing in

Similarly, for 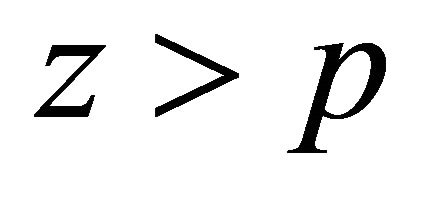we have

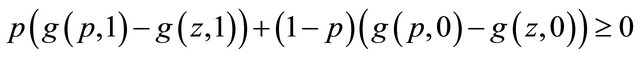
and since

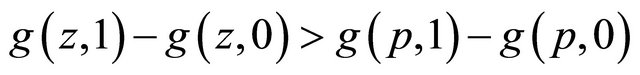
it follows that 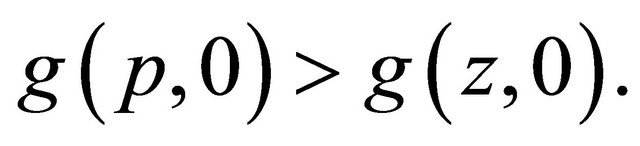So 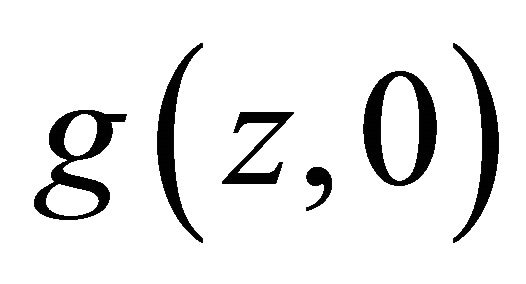strictly decreasing in and hence is strictly increasing.

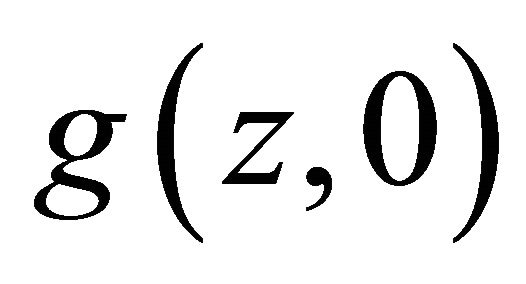From the above two strict monotonicity statements we obtain that and are differentiable almost everywhere. Let 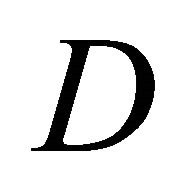be the set where they are differentiable.

For 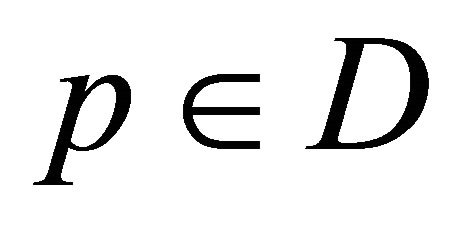and differentiable 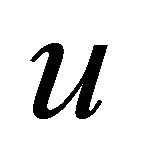we can calculate

and infer that

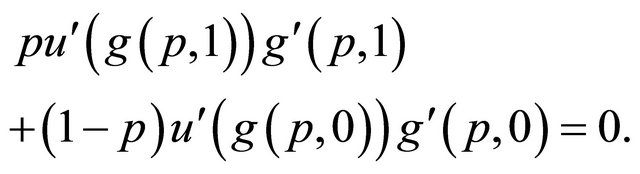(1)

It is easy to argue with generalized version of the intermediate value theorem that there is such that Consider 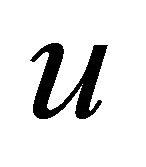that is differentiable with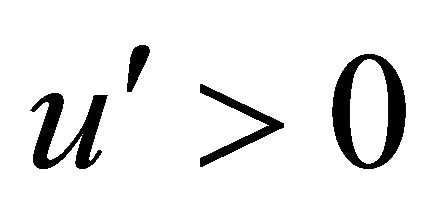. Then rewrite (1) as:

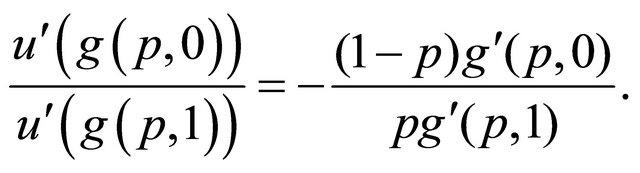(2)

Since 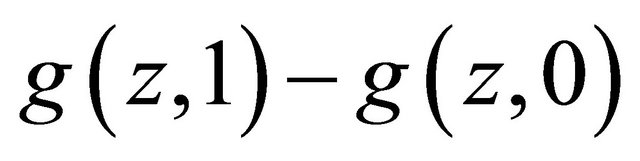is strictly increasing in there is some 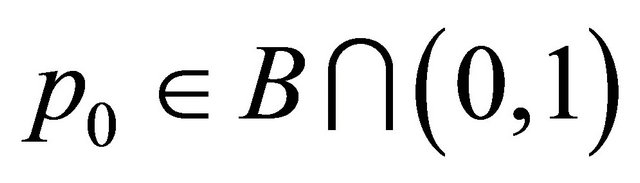such that

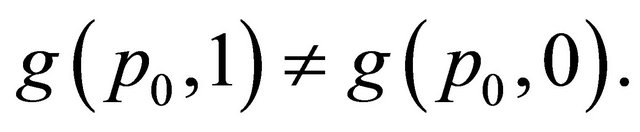So when the left hand side of (2) depends on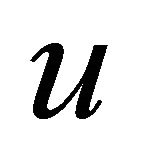. Therefore, (2) cannot hold for all.

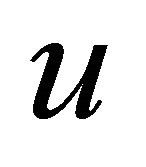NOTES

¹Smith [6, p. 13] writes that the idea is “adapted from Savage [7]”. However, Savage [8, p. 785] 1971 clearly attributes the idea to Smith [6]. Roth and Malouf [9] were the first to induce risk neutrality in this way in an experiment.

²Other authors have independently worked on similar mechanisms. Hossain and Okui [13] presents a randomized mechanism for eliciting the mean of a symmetric distribution, allowing for unbounded support with some additional restrictions. Harrison et al. [14] considers a version of the rQSR (see below), which they call the Binary Lottery Procedure. Both papers also consider non-expected utility theory.