Theoretical Economics Letters
Vol. 2 No. 1 (2012) , Article ID: 17353 , 9 pages DOI:10.4236/tel.2012.21006
Two-Part Tariff Lottery: A Means to Provide Public Good at the Social Optimum
1School of Development Economics, National Institute of Development Administration, Bangkok, Thailand
2Department of Economics, University of Ottawa, Ontario, Canada
Email: amornrat.a@nida.ac.th, vbarham@uottawa.ca
Received November 2, 2011; revised December 14, 2011; accepted December 20, 2011
Keywords: Non-Profit Firms; Lottery; Public Goods; Two-Part Tariff
ABSTRACT
Pure public goods provided by charitable organizations may be provided at the first-best level when the provision is financed by an appropriately designed lottery. If lottery tickets are sold using a two-part tariff, the level of provision of the public good is greater than when fees are not charged to participate in the lottery. Unlike [13] who asymptotically approach the first-best level of provision with an arbitrarily large prize, a Pareto efficient level of the public good is produced when participation fees for the lottery are set appropriately.
1. Introduction
When [1] first presented formal conditions for the efficient provision of pure public goods, he identified two questions that have been at the heart of the research agenda in public economics ever since; namely, how can (and should) public goods be financed, and how can citizens be induced to voluntarily reveal their tastes for these goods. Efforts to address the first issue—the appropriate distribution of the fiscal burden associated with the provision of public goods—have of course inspired much of modern taxation theory (and debates over the virtues of such concerns as horizontal and vertical equity, considerable thoughtful reflection by economist-philosophers (e.g., [2]), and of course the extensive literature on the theory of pricing of public sector services, including that which deals directly with [3] (or benefit-principle) pricing. Finding means to induce citizens to reveal their demand for public goods has also proven to be a considerable challenge, with work on the Clarke-Groves-Vickery mechanisms [4] and, more recently, the serial cost sharing mechanism [5] being merely two examples of the different approaches that have been taken to addressing this issue.
While some public goods—such as national defense —are typically provided by the public sector, others— such as much medical research—are often provided on a voluntary basis by the private sector. Thus a third fecund line of research has been the analysis of the voluntary provision of public goods, which was first studied by [6]. The key issues of interest have been whether or not voluntary mechanisms will generate efficient levels of provision of the public good, and whether or not public policy instruments may be used to influence the equilibrium outcomes. A classic analysis is that of [7], who apply the tools of non-cooperative game theory to the analysis of a subscription game: in a setting of complete information, each consumer is required to decide how much income to voluntarily contribute to financing the provision of the public good. All participants move simultaneously, and it is shown that at the Nash equilibrium of this game an inefficiently low level of the public good is provided. Essentially, this is because any individual contributor perceives himself as the marginal financier, bearing the entirety of the burden of any increase in the level of provision of the public good. It will typically be the case that, at equilibrium, only a subset of citizens will contribute to financing the provision of the public good, and the others free ride.
Considerable effort has subsequently been devoted to identifying ways of improving the performance of the subscription mechanism. Not surprisingly, much work (see, for example, [8,9]) has focused on the usefulness of appropriate public policy instruments. Their conclusions are mixed, as the effectiveness of particular measures is generally affected by whether or not citizens fully understand the public sector budget constraint. The design of the voluntary contributions game has also been considered in detail—researchers have examined whether the results are affected if citizens make contributions sequentially rather than simultaneously, or over time rather than in a static context [10-12].
A particularly interesting recent extension to the [7] model is that of [13], who combines the standard voluntary contributions model with a lottery. He proves that when the opportunity to win a fixed-prize raffle is offered to the contributors to the subscription game, it is possible to obtain a level of provision of the public good that is superior to the level provided at the equilibrium of the classic voluntary contribution game. Furthermore, the level of provision can come very close to the first-best outcome if the prize amount is sufficiently large, but the level of provision cannot reach the social optimum. In this study, we extend Morgan’s approach by introducing a lottery mechanism that is set up as a two part tariff. Consumers who participate in the lottery (and thus help to finance the provision of the public good) must first purchase a ticket giving them the right to participate. We examine the design of the lottery in different informational environments. In particular, we consider an environment in which the Lottery Corporation has full information about the aggregate distribution of preferences, but the tastes of individual consumers are unknown—that is, there is a sorting problem. We prove that when the revenue generated from the fixed fee is used to finance the prize pool, the level of the public good provided by a two-part lottery game is higher than by Morgan’s fixedprize raffle. It thus is possible using a two-part tariff for the sale of lottery tickets to exactly achieve the first-best outcome with a finite prize pool. Moreover, even when consumers are reluctant gamblers, we show that the twopart tariff model (weakly) dominates the traditional lottery model studied by Morgan. We argue that efficiency gains could be obtained by implementing a non-linear pricing system for charitable and government lotteries.
2. The Model
Following [13] we consider a N-consumer economy where each individual has an endowment ωi of a private good which can be used either directly for the purposes of private consumption or to purchase lottery tickets. The funds collected through the sale of lottery tickets are used to finance both the production of a public good G and the fixed prize R which is awarded to the winner of the lottery. The level of production of the public good is thus equal to total spending on lottery tickets, less whatever is set aside to fund the fixed prize. Denoting lottery tickets bought by consumer i by xi where 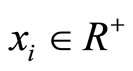 and x (N) is the total amount wagered, we thus have
and x (N) is the total amount wagered, we thus have
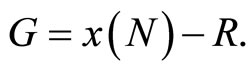 (1)
(1)
Notice that the fixed prize R is selected by the Lottery Corporation and is independent of the number of tickets sold. Unlike [13] we also require that participants pay a (possibly personalized) participation fee of Ti to acquire the right to purchase tickets, in addition to the per-ticket fee. We assume that all of the fixed fees collected are used to fund the prize pool. The total prize pool P is thus defined as:
 (2)
(2)
where T(N) is the total amount of fixed fee collected. The optimal fee structure is determined endogenously at equilibrium by analyzing the decision problem of the Lottery Corporation which may decide to charge a uniform fixed fee, i.e., Ti = T where 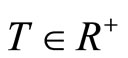 if xi > 0, or a personalized fee
if xi > 0, or a personalized fee . However, when Ti = 0, ∀i, the two-part tariff model is identical to Morgan’s fixed-prize raffle model.
. However, when Ti = 0, ∀i, the two-part tariff model is identical to Morgan’s fixed-prize raffle model.
The prize pool of the lottery is entirely allocated to the winner. Each ticket purchased by a lottery participant is associated with an entry in the lottery, one of which is drawn at random in the final stage of the game. A participant’s likelihood of winning the lottery is therefore equal to the number of tickets s/he holds as a proportion of the total number of tickets sold, that is
 (3)
(3)
where x−i denotes the number of tickets purchased by consumers other than i. Notice that the probability π(•) that a given lottery participant actually wins depends only on the number of tickets that they purchase relative to the total number of tickets purchased, and does not depend directly on the total number of participants in the lottery. As in [13] we assume that consumers have quasilinear utility functions defined over consumption of both the private and the public goods1. Consumers are differentiated both with respect to income, and with respect to their “taste” for the public good, hi(G) A particular individual’s welfare can be expressed as
 (4)
(4)
where we assume that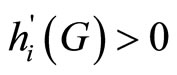 ,and
,and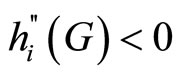 . The optimal level of provision of the public good, G∗, is such that
. The optimal level of provision of the public good, G∗, is such that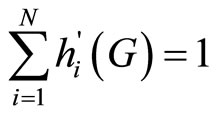 . That is, the social marginal benefit of an additional unit of the provision of public good is equal to the social marginal cost, which in this case is equal to one unit of forgone private consumption.
. That is, the social marginal benefit of an additional unit of the provision of public good is equal to the social marginal cost, which in this case is equal to one unit of forgone private consumption.
We use the tools of non-cooperative game theory to analyze individual behavior in this model. Specifically, we assume that in the first stage, the Lottery Corporation can design the rules of the lottery and then, in the second stage, consumers choose whether or not to participate in lottery and how many tickets to purchase. Subsequently, the public good is produced (using the net proceeds from the lottery), and the winner is determined2. The solution concept is that of sub-game perfect Nash equilibrium, and so the game is solved using backward induction.
2.1. Stage Two: The Consumer’s Problem
We first examine the decision problem faced by consumers in stage two of the game, once the Lottery Corporation has determined the participation fee and the fixedprize. The problem faced by consumers is to allocate their endowment, ωi, between purchasing lottery tickets and private consumption. Whereas expenditure on the private good generates certain benefits, the benefits associated with the purchase of lottery tickets are uncertain, because the purchaser does not know whether or not s/he will win the lottery. Consumer i’s decision problem can thus be expressed as:
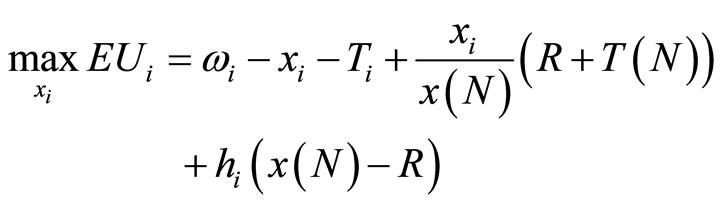 (5)
(5)
The first-order condition for consumer i’s maximizing problem thus becomes:
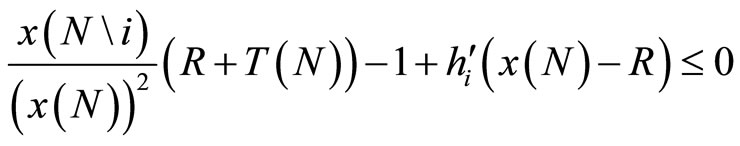 (6)
(6)
We shall define 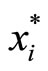 (R, T(N), x(N\i)) to be the solution to the above program. Notice that if T(N) = 0, that is without the fixed fee, Equation (6) would be the first-order condition of the fixed prize raffle in [13]. In addition, if both R and T(N) are zero, there is no lottery game; Equation (6) is the first-order condition of the standard voluntary provision model as presented by [7]. The introduction of the lottery scheme therefore influences the consumer’s decision to support the provision of the public good. The first term of Equation (6),
(R, T(N), x(N\i)) to be the solution to the above program. Notice that if T(N) = 0, that is without the fixed fee, Equation (6) would be the first-order condition of the fixed prize raffle in [13]. In addition, if both R and T(N) are zero, there is no lottery game; Equation (6) is the first-order condition of the standard voluntary provision model as presented by [7]. The introduction of the lottery scheme therefore influences the consumer’s decision to support the provision of the public good. The first term of Equation (6),
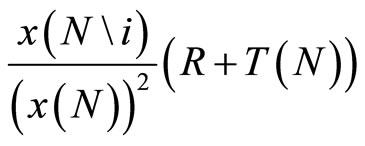
is consumer i’s marginal chance to win the prize pool if s/he purchases an additional ticket. It is, therefore, consumer i’s expected income from winning the lottery. Importantly, the addition of the lottery mechanism affects the comparative statics of the consumer’s donation decision. Whereas in the standard model the consumer perceives the marginal cost of an additional unit of the public good as being equal to $1 (one unit of the private consumption forgone), the integration of the lottery element lowers the marginal cost of contributions by an amount equal to the expected income if consumer i wins lottery. This means that more consumers are now willing to participate in financing the provision of public good. Notice also that, due to the assumed quasi-linearity of the utility function, 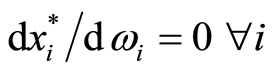 that is, ticket purchasers with the same taste for the public good but different incomes will acquire the same number of tickets.
that is, ticket purchasers with the same taste for the public good but different incomes will acquire the same number of tickets.
As noted earlier, as compared to [13] the key innovation of the approach taken here is that we consider a lottery mechanism that is designed as a two-part tariff. Whereas Morgan funds the prize pool entirely out of ticket sales, in this paper the prize pool is funded firstly from participation fees, and may then be “topped up” out of ticket sales. In fact, it is straightforward to show that funding the prize pool out of revenue generated through collecting participation fees is preferable to skimming off some proportion of total ticket sales.
Proposition 1: The increase in the level of provision of the public good resulting from an incremental increase in Ti is greater than the increase in the level of provision of the public good resulting from an equal incremental increase in R.
Proof. Suppose that only n′ consumers, where n′ ≤ N, choose to bet a positive amount on the lottery. The first order condition for the n′ bettors can be written as:
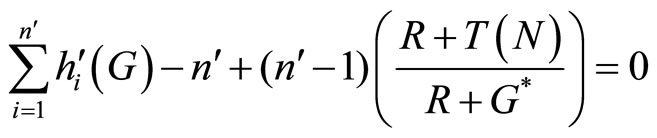 (7)
(7)
Recall that G∗ = x (N) − R. Totally differentiating this expression with respect to G∗, R and Ti yields the following expressions:
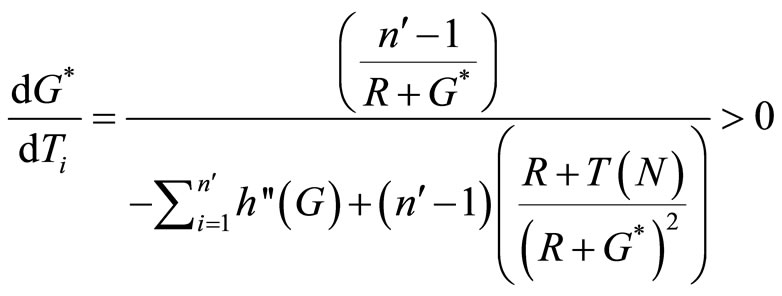 (8)
(8)
 (9)
(9)
and it is immediate from comparing these two inequalities that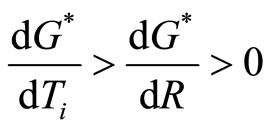 .
.
Proposition 1 show that to increase the level of provision of the public good it is more effective to increase the jackpot via an increase in the participation fee rather than to divert equivalent funds from total spending on lottery tickets to the prize pool. This will be of relevance in identifying the optimal policy for the Lottery Corporation. It is also interesting to observe that
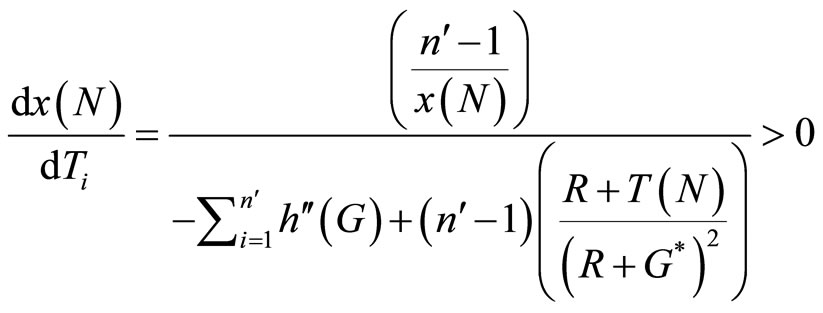 (10)
(10)
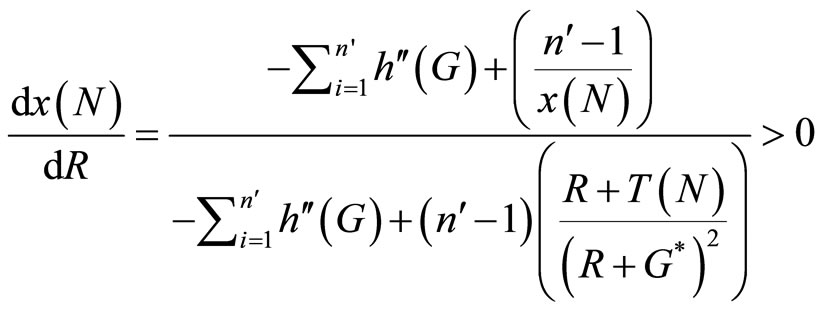 (11)
(11)
and therefore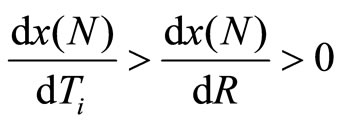 . That is, a $1 increase in the fixed-prize will increase the total amount wagered by less than a $1 increase in participation fee. This is because ceteris paribus an increase in R decreases the level of provision of the public good, whereas an increase in Ti has no direct impact on the level of G∗, it turns out that the level of provision of the public good actually rise more when incremental increases in the prize pool are funded out of the increased participation fees rather than by diverting a larger proportion of ticket revenue to the prize pool. Notice also that since the fixed fee is a better instrument than the fixed-prize, Proposition 1 implies that the provision of public good by the twopart tariff lottery mechanism is a Pareto improvement as compare to the provision of public good by the simple fixed-prize raffle mechanism.
. That is, a $1 increase in the fixed-prize will increase the total amount wagered by less than a $1 increase in participation fee. This is because ceteris paribus an increase in R decreases the level of provision of the public good, whereas an increase in Ti has no direct impact on the level of G∗, it turns out that the level of provision of the public good actually rise more when incremental increases in the prize pool are funded out of the increased participation fees rather than by diverting a larger proportion of ticket revenue to the prize pool. Notice also that since the fixed fee is a better instrument than the fixed-prize, Proposition 1 implies that the provision of public good by the twopart tariff lottery mechanism is a Pareto improvement as compare to the provision of public good by the simple fixed-prize raffle mechanism.
Corollary 1: Introducing a small and positive amount of entry fee into Morgan’s fixed-prize raffle mechanism can help to increase the level of public good provided.
Proof. When (6) is zero, this implies that if consumer i is a bettor in the fixed-prize raffle game, s/he would be a bettor in the two-part tariff lottery game, as long as the entrance fee is relatively a small proportion of i’ s wealth. And Proposition 1 shows that as long as the total amount of the participation fees is used to financed the prize pool, the level of the public good provided will increase by more than it would were the Lottery Corporation to increase the size of the fixed-prize by the same amount. Both Proposition 1 and Corollary 1 are consistent with Theorem 2 of [13] which shows that the level of the public good provided under the fixed-prize raffle will grow as the fixed-prize amount R increases. He also proves that society would be better off if the marginal donation were used to increase the prize pool rather than the provision of the public good directly. This is the effective consequence of introducing a two-part tariff lottery, because all the participation fees are used to finance the prize pool. With quasi-linear preferences an optimallydetermined fixed-fee can lead to the first-best level of the provision of public good. However, when the fixed fee becomes larger, we need to ensure that the participation constraint is satisfied3.
Proposition 2. When the participation constraint is satisfied, the level of the public good financed by the twopart tariff lottery is Pareto efficient when T(N) = G∗.
Proof. Recall that when the public good is provided at the first-best level, . Combining this condition with the first-order condition of all n′ bettors in (7), we have
. Combining this condition with the first-order condition of all n′ bettors in (7), we have
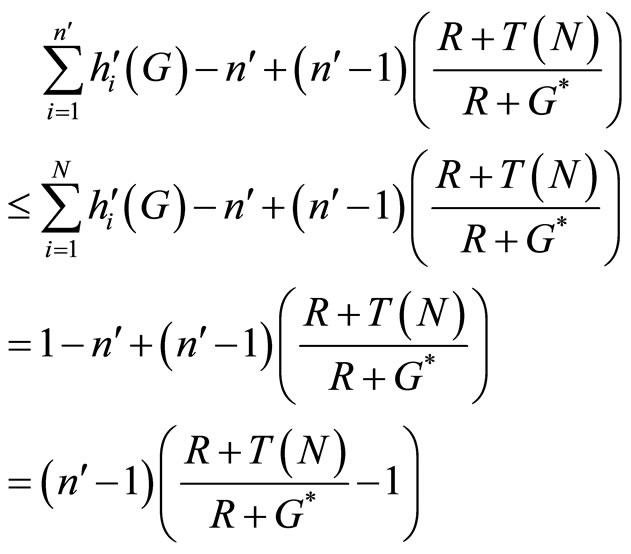 (12)
(12)
Now set T (N) = G∗. Then the right-hand side of Equation (12) equals zero. This implies that the level of public good provided by n′ bettors voluntarily choosing to participate in the two-part tariff lottery game is at the firstbest level.
Corollary 2: When the participation constraint is satisfied and T(N) = G∗, only those who benefit from the public good will choose to participate in the lottery. Those who choose not to participate have zero benefit.
Proof. From the above proposition, we show that
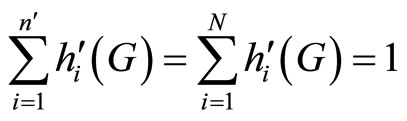 , for the
, for the  bettors. This implies that
bettors. This implies that  given that
given that  is the number of non-bettors, and
is the number of non-bettors, and 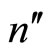 = N –
= N –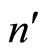 . Note that for
. Note that for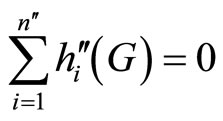 it must be true that
it must be true that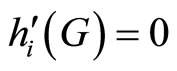 , for all i in the set of nonbettors for the marginal benefit from the consumption of public good cannot be negative.
, for all i in the set of nonbettors for the marginal benefit from the consumption of public good cannot be negative.
The above results (and those of [13]) are of course critically dependent on the assumed risk neutrality of consumers. This feature of the utility function means that the individual consumer’s decision with respect to the number of lottery tickets to purchase depends only on two factors: the private marginal benefit of an additional unit of the public good and the marginal impact on the individual’s chance of winning the prize pool. Increasing the prize pool by charging a participation fee thus increases the purchase of lottery tickets, as it increases the benefits of winning4. If consumers were risk averse, it cannot be assumed that the increased expected benefits of winning would compensate for the increase in the variability of income.
Notice that the optimal amount of G∗ that the Lottery Corporation uses to set up the fixed-fee requires only that the Lottery Corporation know the distribution of preferences in the population—rather than knowing what individual preferences are. In other words, the Lottery Corporation needs to know only that there are, say, 1500 high demanders and 2500 low demanders for the public good—but does not need to know which individuals are high demanders, and which individuals are low demanders. It is also worth underscoring that the Lottery mechanism is available to non-profit organizations which do not have any taxing powers.
2.2. Stage One: The Lottery Corporation’s Problem
We next consider the problem faced by the Lottery Corporation in stage one. We assume that the Lottery Corporation wishes to design the lottery to maximize social welfare; this assumption is appropriate if it assumed that the Corporation is publicly owned, but is less compelling if the lottery is operated by a private charity. In designing the lottery, the two instruments available to the Corporation are Ti, the participation fee to be paid by consumer i, and R, the amount of ticket revenue to be siphoned off to fund the prize pool rather than the provision of the public good. We assume that, as in models of adverse selection, the Corporation has complete information about the distribution of aggregate preferences, but does not know the type of a particular consumer. We assume a Benthamite social welfare function SWF, and so the Lottery Corporation’s problem can be expressed as:
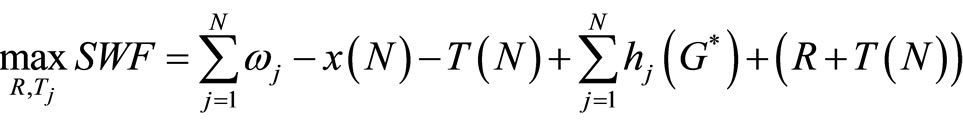 Subject to
Subject to 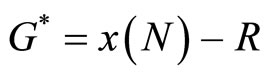 (13)
(13)
Recall that the number of tickets purchased by i depends on 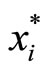 (R, T (N), x(N\i)). The first-order necessary conditions for the Corporation are:
(R, T (N), x(N\i)). The first-order necessary conditions for the Corporation are:
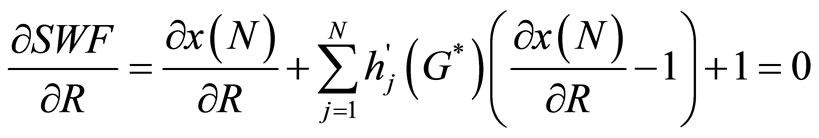 (14)
(14)
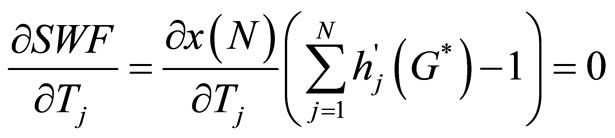 (15)
(15)
Rewriting Equation (14), we see that when R is chosen optimally, it must be true that
 (16)
(16)
If the public good is provided optimally, we know that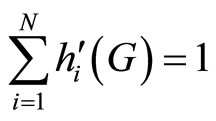 . So (16) thus implies either that the optimal level of the public good must be provided in equilibrium, or
. So (16) thus implies either that the optimal level of the public good must be provided in equilibrium, or , or both conditions must be true simultaneously. If an inefficient level of the public good were to be provided (as is the case with Morgan’s model) it must be true that, at the margin, all additional funds collected are diverted to funding the prize pool and there is no net increase in the level of provision of the public good. This observation explains Morgan’s result that the fixed-prize raffle cannot be used to implement the first-best level of provision of the public good, since in his model the prize pool must be funded out of ticket revenue, and there is no possibility of using participation fees to cover some portion of the total cost of the prize pool.
, or both conditions must be true simultaneously. If an inefficient level of the public good were to be provided (as is the case with Morgan’s model) it must be true that, at the margin, all additional funds collected are diverted to funding the prize pool and there is no net increase in the level of provision of the public good. This observation explains Morgan’s result that the fixed-prize raffle cannot be used to implement the first-best level of provision of the public good, since in his model the prize pool must be funded out of ticket revenue, and there is no possibility of using participation fees to cover some portion of the total cost of the prize pool.
Turning to Equation (15), and recall from (10) that
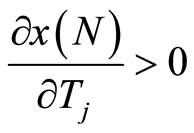 , we note that (15) cannot be satisfied unless the optimal level of the public good is provided. In other words, as long as the outcome of stage two is such that consumers spend too little on lottery tickets, resulting in under provision of the public good, the Lottery Corporation can increase social welfare by cranking up the participation fee, and by so doing will increase the aggregate level of provision of the public good. Notice, however, that if (15) is satisfied, then (14) is satisfied for any fixed prize amount. That is, social welfare is now independent of R. The Corporation’s solution thus is consistent with consumers’ solution: as long as the total amount collected from participation fees is equal to the optimal level of public good, and when the participation constraint is satisfied all those who have positive benefit on the public good will participate in lottery. And so we shall restrict ourselves to the case where the prize pool is entirely financed out of the participation fees, and all spending on lottery tickets is used to fund the provision of the public good.
, we note that (15) cannot be satisfied unless the optimal level of the public good is provided. In other words, as long as the outcome of stage two is such that consumers spend too little on lottery tickets, resulting in under provision of the public good, the Lottery Corporation can increase social welfare by cranking up the participation fee, and by so doing will increase the aggregate level of provision of the public good. Notice, however, that if (15) is satisfied, then (14) is satisfied for any fixed prize amount. That is, social welfare is now independent of R. The Corporation’s solution thus is consistent with consumers’ solution: as long as the total amount collected from participation fees is equal to the optimal level of public good, and when the participation constraint is satisfied all those who have positive benefit on the public good will participate in lottery. And so we shall restrict ourselves to the case where the prize pool is entirely financed out of the participation fees, and all spending on lottery tickets is used to fund the provision of the public good.
Proposition 3. When the consumer participation constraint is satisfied, and the prize pool is funded entirely out of participation fees, then at a sub-game perfect Nash equilibrium the Lottery Corporation sets participation fees such that T(N) = G∗.
Proof. From corollary 2 we shows that
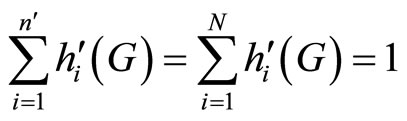 , therefore, at any sub-game perfect equilibrium (15) must be satisfied, and a first-best level of the public good must be provided. Given R = 0, then (7) is immediately evident that T(N) = G*.
, therefore, at any sub-game perfect equilibrium (15) must be satisfied, and a first-best level of the public good must be provided. Given R = 0, then (7) is immediately evident that T(N) = G*.
Proposition 4. When the Lottery Corporation sets Ti = T = G∗/N, the optimal level of the public good is provided at the sub-game perfect Nash equilibrium of the Lottery Game, and when the participation constraint is satisfied, all bettors pay their Lindahl price for consumption of the public good.
Proof. By construction, T(N) = G*, R = 0 implies G∗ = x(N). From consumer’s first-order condition in (6) we have that
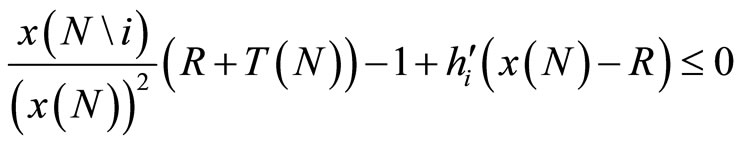 (17)
(17)
Notice that at the sub-game perfect Nash, x∗(N\i) = x(N) − , and substitute T(N) = G∗ = x(N), when R = 0 we obtain
, and substitute T(N) = G∗ = x(N), when R = 0 we obtain
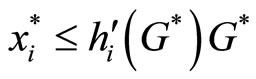 (18)
(18)
however, if i is the bettor, the first-order condition of utility maximizing in (6) must be satisfied with equality, i.e., 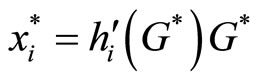 , that is bettor i buys lottery tickets exactly equal to his Lindahl price. On the contrary, since the corollary 2 shows that if i is a non-bettor,
, that is bettor i buys lottery tickets exactly equal to his Lindahl price. On the contrary, since the corollary 2 shows that if i is a non-bettor, 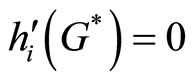 , therefore,
, therefore, 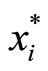 = 0 for all non-bettors.
= 0 for all non-bettors.
What the above proposition establishes, therefore, is that even when the Lottery Corporation is faced with a problem of adverse selection, citizens will choose to reveal their demands for the public good by expending on the purchase of tickets an amount equal to their Lindahl price, as long as the aggregate value of participation fees levied is equal to total expenditure on the public good. Notice that the Corporation does not know how many people are bettors and how many are non-bettors. The Corporation simple set the participation fee at the level of public good provision per capita. When the participation constraint is satisfied, all consumers choose to reveal their true preference for the public good.
Our results rely heavily on the assumption that the participation constraint is satisfied—consumers who have positive benefit from the public good must be willing to purchase lottery tickets. But it is always the case in models of the voluntary provision of public goods that citizen have the option of “playing the lottery”, or freeriding. A particular consumer will choose to participate if and only if their expected utility when they participate exceeds their expected utility were they to free-ride. In particular, we observe that if all other participants choose 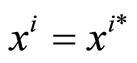 then EUi (participates) ≥ EUi (not participates)
then EUi (participates) ≥ EUi (not participates)
If and only if:
 (19)
(19)
Note that we can restrict attention to xi = 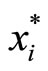 since, if individual i participates in the lottery game, their contribution level will be determined by (6). Using the equilibrium conditions for the Lottery Corporations’ decision, we can rewrite (19) as EUi (participates) ≥ EUi (not participates)
since, if individual i participates in the lottery game, their contribution level will be determined by (6). Using the equilibrium conditions for the Lottery Corporations’ decision, we can rewrite (19) as EUi (participates) ≥ EUi (not participates)
If and only if:
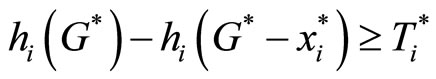 (20)
(20)
To summarize the results of the above analysis: for all consumers whose marginal benefit from the provision of public good is positive, even under an imperfect information about individual preferences, the Lottery Corporation can implement a first-best outcome in which all citizens pay their Lindahl price for the public good by charging a uniform participation fee equal to the per capita level of provision of the public good. Citizens whose condition (20) is satisfied will participate, and will purchase a quantity of lottery tickets of a total value equal to their Lindahl price for the public good. Notice that with a uniform entry fee, the participation constraint (20) will generally be satisfied if the population N is big enough, or if all individuals have a high demand for the public good.
3. The Optimal Provision When Some Consumers Are Reluctant Gamblers
If the participation constraint (20) is not verified for T = , and the Lottery Corporation does not have the power to tax citizens, then the Corporation would need to re-design the lottery pot. In essence, the participation constraint fails to hold when the benefits associated with the lottery are not big enough: they are reluctant to gamble unless the gains associated with winning are really big. This means that the Lottery Corporation will have to find other means of “sweetening the pot”, and the most obvious route to doing so is to divert some proportion of ticket sale revenue to funding the prize pool, rather than relying exclusively on participation fees. In this section, we consider the Lottery Corporation’s problem when individuals must be enticed to participate in the Lottery and so the Corporation must use both R and T to fund the prize pool.
, and the Lottery Corporation does not have the power to tax citizens, then the Corporation would need to re-design the lottery pot. In essence, the participation constraint fails to hold when the benefits associated with the lottery are not big enough: they are reluctant to gamble unless the gains associated with winning are really big. This means that the Lottery Corporation will have to find other means of “sweetening the pot”, and the most obvious route to doing so is to divert some proportion of ticket sale revenue to funding the prize pool, rather than relying exclusively on participation fees. In this section, we consider the Lottery Corporation’s problem when individuals must be enticed to participate in the Lottery and so the Corporation must use both R and T to fund the prize pool.
If citizens are sufficiently wealthy, then by increasing the size of the prize pool sufficiently it is possible to attain the first-best even when citizens are reluctant gamblers. Recall from (19), to ensure consumers’ participation, it must be true that
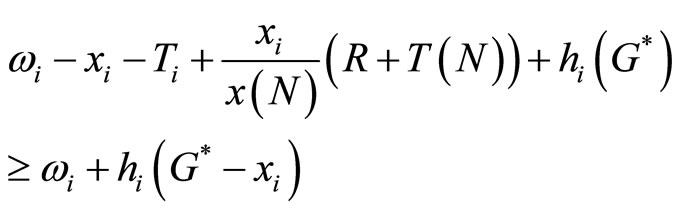 (21)
(21)
Or;
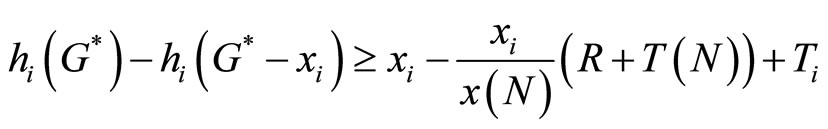 (22)
(22)
assume that the Corporation chooses Ti = T ∀i, we also observe from the weak concavity of hi(G) that
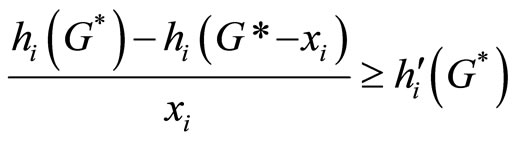 (23)
(23)
and from the bettor’s first-order condition we have that

that is,
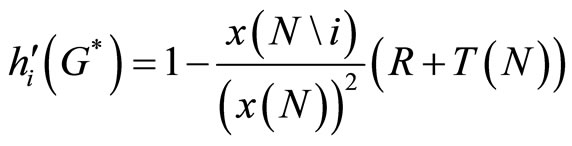 (24)
(24)
Substituting (24) into (23), we get
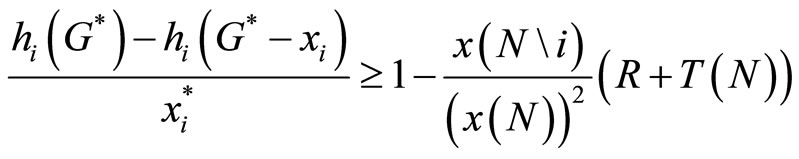
or,
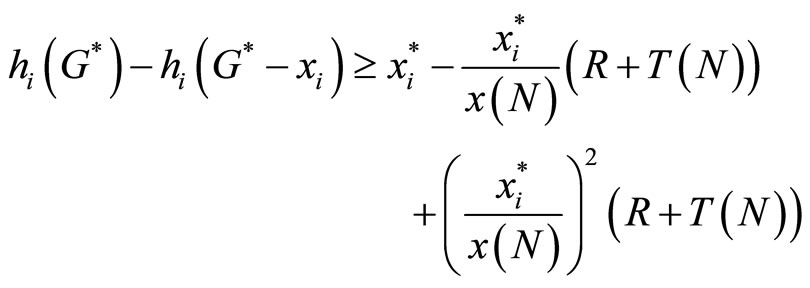 (25)
(25)
Since (25) is always true, compare (22) with (25). For (22) to hold, we would set the last term on the right-hand side of (22) such that
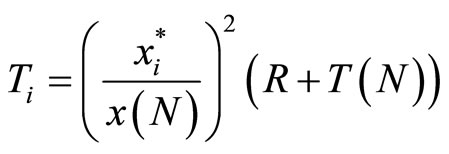 (26)
(26)
or,
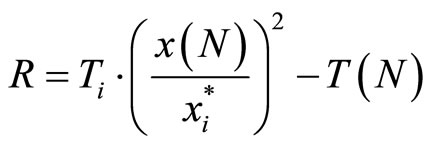 (27)
(27)
Notice that 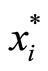 depends on consumer i’s preference on G∗. Therefore, if the Corporation has perfect information about consumers’ preference, the Corporation would be able to charge the personalized fee Ti to ensure that the participation constraint (26) will hold. (Of course, we have to assume that no one is too poor to pay the fixedfee.)
depends on consumer i’s preference on G∗. Therefore, if the Corporation has perfect information about consumers’ preference, the Corporation would be able to charge the personalized fee Ti to ensure that the participation constraint (26) will hold. (Of course, we have to assume that no one is too poor to pay the fixedfee.)
However, it is unlikely that the Corporation would know each individual’s preference. It is more practical to assume that the Corporation knows consumers partially, i.e., the Corporation only knows the aggregate preference and its boundary. To ensure that everyone whose marginal benefit from the provision of public good is positive will participate, the Corporation therefore charges fixed-fee Ti = T, and set 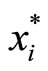 =
= 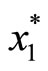 where
where 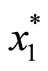 is the optimal amount of tickets purchased by the lowest demand consumer (i.e., 0 <
is the optimal amount of tickets purchased by the lowest demand consumer (i.e., 0 < 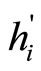 (G∗), ∀i). We now can consider the Corporation’s maximizing problem:
(G∗), ∀i). We now can consider the Corporation’s maximizing problem:
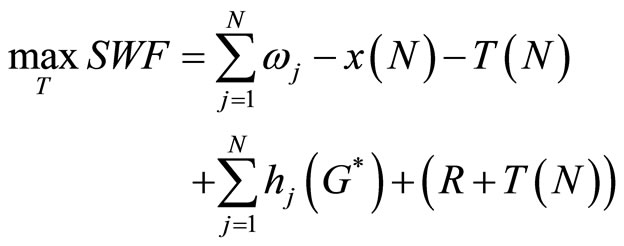 (28)
(28)
subject to G∗ = x(N) – R, and 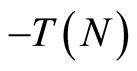
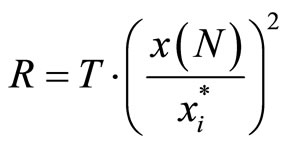
Notice that, in this case, T(N) = NT; therefore, the firstorder necessary condition for the Corporation’s problem thus becomes:
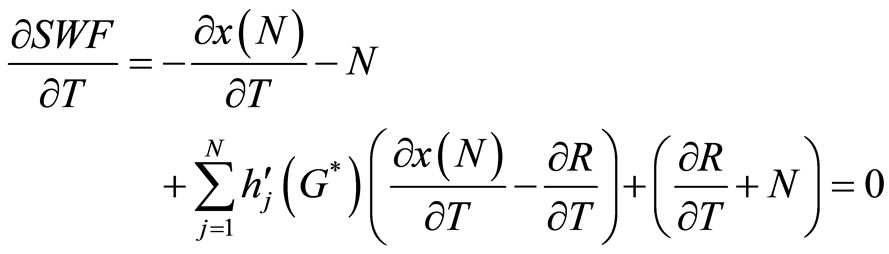
 (29)
(29)
Notice that as long as , therefore it must be the case that
, therefore it must be the case that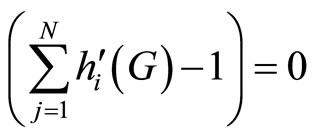 , i.e., the provision of public good attains its optimum.
, i.e., the provision of public good attains its optimum.
Re-write consumer’s first-order necessary condition, (24), when i is the bettor, we obtain
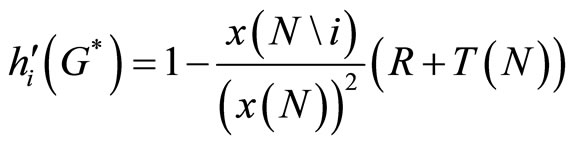
Using the participation constraint that 
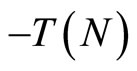 implies that
implies that
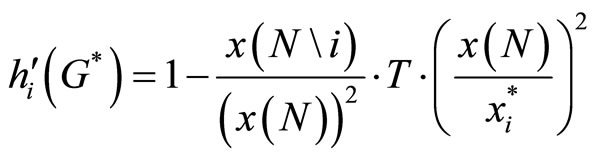 (30)
(30)
Since x(N\i) = x(N) −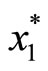 , therefore:
, therefore:

or,
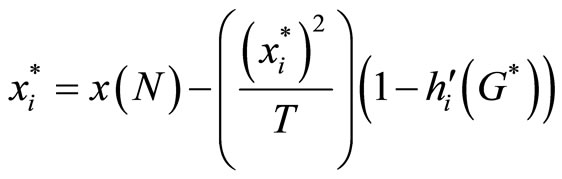 (31)
(31)
In addition, we can find the relation between T and x(N) by summing up all the  bettors’ first-order condition in (30) as follow:
bettors’ first-order condition in (30) as follow:
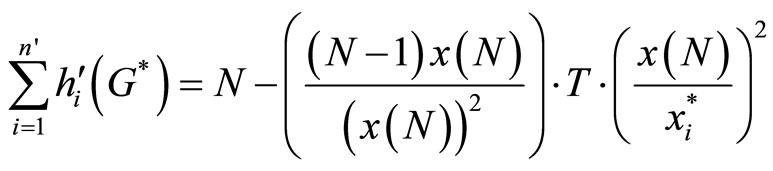 (32)
(32)
Recall that 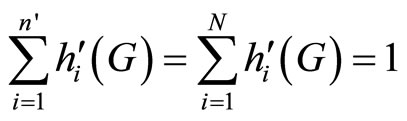 when G∗ is at optimum, that is
when G∗ is at optimum, that is
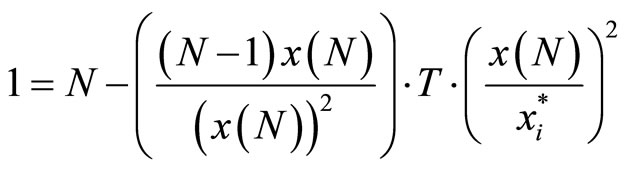
Straightforwardly re-arranging the terms, we obtain
 (33)
(33)
Substituting (33) into (31) and using the fact that G∗ = x(N) − R, we finally obtain that
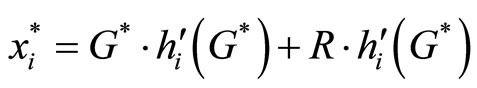
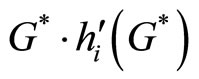 is the Lindahl price for the consumption of public good. In the previous model where there is no fixed prize, i.e. R = 0, consumers buy tickets equal to their Lindahl price for the consumption of public good as long as those who have a positive marginal benefit on the consumption of public good will choose to participate in lottery. Actually, it is the case when consumer’s utility function is not overly concave in G. But when consumers are reluctant gamblers the Corporation has to use the fixed prize, R, to draw consumers’ attraction to lottery. Since we set R such that even the lowest demand consumer is willing to participate,
is the Lindahl price for the consumption of public good. In the previous model where there is no fixed prize, i.e. R = 0, consumers buy tickets equal to their Lindahl price for the consumption of public good as long as those who have a positive marginal benefit on the consumption of public good will choose to participate in lottery. Actually, it is the case when consumer’s utility function is not overly concave in G. But when consumers are reluctant gamblers the Corporation has to use the fixed prize, R, to draw consumers’ attraction to lottery. Since we set R such that even the lowest demand consumer is willing to participate, 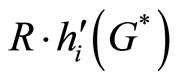 is therefore the extra tickets that consumer buys because of the attracttiveness of the fixed prize.
is therefore the extra tickets that consumer buys because of the attracttiveness of the fixed prize.
4. Conclusions
This paper extends [13] by introducing a lottery mechanism that is set up as a two part tariff. When the participation fee is chosen appropriately, the first-best level of the public good will be provided by the lottery mechanism. Thus we would recommend that the Lottery Corporation or charities that raise funds by means of lotteries consider the possibility of implementing a two part tariff lottery. One limitation on the implementation of such a system may be the practice of regular lottery-ticket purchasers to pool together their purchases.
This analysis is developed under the assumption that individuals have quasi-linear utility functions; this means that consumers are risk-neutral, and that the distribution of income is irrelevant to the determination of social welfare. Clearly, it would be desirable to work with a general concave utility function; however, results are much more difficult to interpret. Other interesting extensions would be to examine the impact of rivalry amongst lottery providers: our study has only one lottery pot in the model, but in reality there exist many charities that run lotteries at the same time—how does this affect consumer behavior? In the same vein, many charities run lotteries with two drawings. Thus two stage lottery games deserve to be considered as well.
REFERENCES
- P. A. Samuelson, “The Pure Theory of Public Expenditure,” Review of Economics and Statistics, Vol. 36, No. 4, 1954, pp. 387-389. doi:10.2307/1925895
- P. Van Parijs, “Real Freedom for All: What (If Anything) Can Justify Capitalism?” Oxford Political Theory Series, Oxford University Press, Clarendon Press, Oxford and New York, 1995, p. xii, 330.
- E. Lindahl, “Just Taxation—A Positive Solution,” In: R. A. Musgrave and A. T. Peacock, Eds., Classic in the Theory of Public Finance, Macmillan, London, 1967, pp. 168-176.
- J. Green and J. J. Laffont, “Incentives in Public Decision Making,” North-Holland, Amsterdam, 1979.
- H. Moulin, “Serial Cost-Sharing of Excludable Public Goods,” The Review of Economic Studies, Vol. 61, No. 2, 1994, pp. 305-325. doi:10.2307/2297983
- M. Olson, “The Logic of Collective Action,” Harvard University Press, Cambridge, 1965.
- T. Bergstrom, L. Blume and H. Varian, “On the Private Provision of Public Goods,” Journal of Public Economics, Vol. 29, No. 1, 1986, pp. 25-49. doi:10.1016/0047-2727(86)90024-1
- R. Boadway, P. Pestieau and D. Wildasin, “Tax-Transfer Policies and the Voluntary Provision of Public Goods,” Journal of Public Economics, Vol. 39, No. 3, 1989, pp. 157-176. doi:10.1016/0047-2727(89)90038-8
- M. Bilodeau and A. Slivinski, “Toilet Cleaning and Department Chairing: Volunteering a Public Service,” Journal of Public Economics, Vol. 59, No. 3, 1996, pp. 299- 308. doi:10.1016/0047-2727(94)01494-9
- C. Fershtman and S. Nitzan, “Dynamic Voluntary Provision of Public Goods,” European Economic Review, Vol. 35, No. 5, 1991, pp. 1057-1067. doi:10.1016/0014-2921(91)90004-3
- M. Gradstein, “Time Dynamics and Incomplete Information in the Private Provision of Public Goods,” Journal of Political Economy, Vol. 100, No. 3, 1992, pp. 581-597. doi:10.1086/261830
- H. R. Varian, “Sequential Contributions to Public Goods,” Journal of Public Economics, Vol. 53, No. 2, 1994, pp. 165-186. doi:10.1016/0047-2727(94)90019-1
- J. Morgan, “Financing Public Goods by Means of Lotteries,” Review of Economic Studies, Vol. 67, No. 4, 2000, pp. 761-784. doi:10.1111/1467-937X.00153
- B. Duncan, “Financing Charitable Organizations and Non-Profit Firms,” Ph.D. Dissertation, University of California, Santa Barbara, 1998.
NOTES
1On the limitations of using quasi-linear models when considering lottery finance of pure public goods, see [14].
2In fact, the results obtained below depend on the total size of the prize pool, but not on the number of prizes awarded. In particular, the prize pool can be divided into an arbitrary number of prizes, as long as each participant’s chance of winning every prize offered depends only on the number of tickets they purchased as a proportion of all tickets sold. Thus, in particular, it is possible for one individual to win the entire prize pool. For ease of exposition, however, we will continue to refer to “a winner”, when in fact it would be appropriate to talk about “the winners”.
3Consumers will choose to play lottery if and only if their expected utility when they participate in the lottery game is higher than their expected utility if they were to free ride.
4Setting the total fixed fee equals to the optimal level of public good provided actually is consistent with Equation (4) in [13]. The negative externality created by the two-part tariff lottery game completely offsets the positive externality of public good provision. Since the externality no longer exists, the public good is provided at the optimum. This problem could not be solved in [13] fixed-prize raffle model for an increasing in the fixed-prize reduces the net proceed available to fund the provision of public good. We do not have this problem for our prize pool is funded out of tickets revenue.

