Journal of Mathematical Finance
Vol.06 No.05(2016), Article ID:72058,8 pages
10.4236/jmf.2016.65053
Jump Intervals of Stock Price Have Power-Law Distribution: An Empirical Study
Hongduo Cao*, Ying Li*, Huaping He, Zhi He
Sun Yat-sen Business School, Sun Yat-sen University, Guangzhou, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 24, 2016; Accepted: November 14, 2016; Published: November 17, 2016
ABSTRACT
Taking the power-law behavior of human activities into consideration, we conduct an empirical study on the distribution of jump intervals after using BNS nonparametric method to detect jumps in 5 min closing data of HIS. Our result shows that there is a “power law” in jump intervals, and Fokker-Planck distribution is the more suitable distribution to describe jump intervals than the traditional Poisson process. So the jump diffusion model of power law can depict the movement of stock price more accurately.
Keywords:
Stock Price, Jump Intervals, Power-Law Distribution, Human Dynamics

1. Introduction
The price of underlying assets is not only the foundation for financial derivatives pricing, but also plays an important role in the investment decision-making of the investors. Many classical theories assume that asset prices have continuous-time paths, e.g. Black & Scholes’ option pricing formula (hereafter BS formula) [1] . But financial markets sometimes generate significant discontinuities, so-called jumps. Merton [2] put forward the jump diffusion model by combining the continuous sample path and the stochastic jump process together. He used a “Poisson driven” process to describe the “abnormal” vibrations. Because of its concise form and clear logic, Merton’s model has become the standard model in analyzing the discontinuous change of the underlying asset price since it was presented. Under this framework, the follow-up studies generally focus on distribution of jump sizes while accepting that the jump component is a “Poisson driven” process, which means the probability of having jump is the same at any time. Kou’s asymmetric double exponential jump diffusion model [3] has the greatest effect. But in fact, the volatility of financial market will cluster together, that is, the high volatility will be relatively concentrated in certain periods of time, while the concentrated low volatility will present in other periods of time. Obviously, the Poisson process can’t describe such phenomenon.
Lots of studies have showed that human activities are quite uneven: high-frequency outbreaks in short time separate a long time of silence, whose distribution of human activity’s interval presents a deviation from the Poisson process, and is characterized by the power-law distribution with a fat tail. Barabási [4] puts forward that the burst and fat tail in human dynamics are originated in some queuing process-based decision-mak- ing. Human dynamics researches the generation mechanism of non-Poisson behavior, while the models pay attention to the feature of human behavior such as the model based on the model of the human interest or memory [5] , as well as based on social interaction model [6] .
The movement of asset price is the result of many individual investors’ or institutes’ decision-making activities. So there is sufficient reason to believe that the characteristics of the asset price volatility should be consistent with the general statistical law of human activities.
Cao Hong-duo et al. [7] have empirically learned the stochastic features of the jump intervals of the Shanghai composite index. They put forward the jump diffusion model of power law by considering the human dynamics, and this model can depict the sharp kurtosis, fat tail, volatility clustering fairly well.
The distribution of HSI’s jump intervals is empirically researched in this paper in order to further verify the universality of the power law to jump interval.
The rest of the article is organized as follows. Section 2 introduces the candidate models. Section 3 empirically examines the distribution of jump intervals. Finally, we conclude in Section 4.
2. Candidate Models
Merton’s model [2] fails to support the skewness of the return distribution because it assumes that the jump sizes follow the independent identical distribution. Kou’s asymmetric double exponential jump diffusion model [3] overcomes this shortcoming. Kou’s model is as followed,
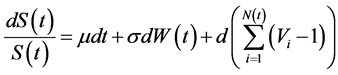 ,
,
where 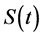 is the asset price,
is the asset price, 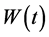 is the standard Brownian motion,
is the standard Brownian motion, 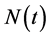 is the Poisson process with rate
is the Poisson process with rate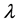 , and
, and 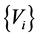 is a sequence of independent identically distributed non-negative random variables.
is a sequence of independent identically distributed non-negative random variables.
Although Kou’s model can explain the skewness of asset returns, it fails to give a description of the volatility clustering. The key to the problem is the assumption to the counting process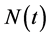 . So next, we will compare the actual effect when
. So next, we will compare the actual effect when 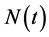 is Poisson process and renewal process with power-law nature respectively. Candidate models that are considered in this paper are setting as follows.
is Poisson process and renewal process with power-law nature respectively. Candidate models that are considered in this paper are setting as follows.
If we use the Poisson process to describe the jump intervals, then the probability density of intervals between two adjacent jumps obey exponential distribution,
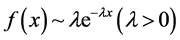 ,
,
where and hereinafter x is the interval between two adjacent jumps, 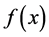 is the probability that jump happens after x. When using the exponential distribution to fit the samples, we choose its common form,
is the probability that jump happens after x. When using the exponential distribution to fit the samples, we choose its common form,
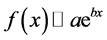 . (1)
. (1)
For the renewal process with power-law nature, we focus on the Fokker-Planck distribution and power law with exponential cutoff. Fokker-Planck distribution is used to describe the time evolution of the probability density function of the velocity of a particle, and its probability density function is
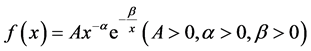 . (2)
. (2)
The power law with exponential cutoff is one of the mixture distributions, and its probability density function is
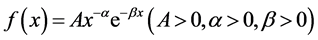 . (3)
. (3)
3. Empirical Study on the Distribution of Jump Intervals
3.1. Jump Detecting Methods
ARCH class of models and SV class of models are two classical parametric methods in depicting the volatility of asset price. However, non-parametric method, which is based on facts and all sample data and doesn’t have complicated parameter estimations, has an unparalleled advantage over parametric method. For the outcomes of parametric method are just approximations of the historical data. The non-parametric methods that are often used in previous studies to describe the volatility of asset price are quadratic variation and bi power variation (hereafter BPV). And it has been proved that the realized BPV can be used to consistently estimate the integrated volatility, even there are jumps in return processes [8] .
The BPV which is put forward by Barndorff-Nielsen and Shephard [8] [9] , is one of the recent breakthroughs in non-parametric methods to detect jumps that has great implication. The basic intuition behind this detection technique is that estimating the quadratic variation of the log-price and its continuous part for a certain unit of time respectively, and if they are equal, then there is no jump in this unit of time, otherwise, jump exists. Accordingly, we use the ratio jump statistic constructed by Barndorff- Nielsen and Shephard [9] (hereafter BNS) to detect jumps.
The jump detecting method is as follows:
Dividing a day-trading-time into M intervals, M + 1 datum will be observed as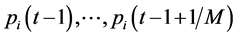 .
. 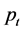 is the Log-price of a single asset, p is assumed to be Brownian semi-martingale plus jump. The jth payoff in a trading day is noted as
is the Log-price of a single asset, p is assumed to be Brownian semi-martingale plus jump. The jth payoff in a trading day is noted as
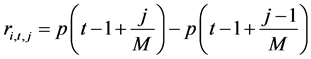 . Realized volatility is defined by
. Realized volatility is defined by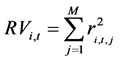 . The bipower variation is defined as
. The bipower variation is defined as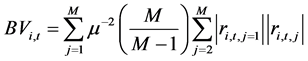 , where
, where





3.2. Data Acquisition and Processing
We use 5 min closing data of HIS (Hang Seng Index in Hong Kong stock) as our research object. Because of the constraint of data availability, the time span of our data is 13 weeks or 64 trading days (Hong Kong stock market closed for one day on 2 July 2012 (Monday) because of the 15th Hong Kong Special Administrative Region Establishment Day), from 09:35 on 28 May 2012 to 16:00 on 24 August 2012. The total sample size is 4224 and they are all collected from tdx.com.cn Corporation.
Although BNS suggests
3.3. Results of Jump Detection and Frequency Statistics of Jump Intervals
According to BNS, if the ratio jump statistic is smaller than its corresponding 95% critical value, then we reject the hypothesis of no jump in this unit of time. We detect 86 jumps altogether, as shown in Figure 1.
Make a subtraction between two adjacent jumps’ numbers, we can get a jump interval. There are 85 jump intervals in this study, and the smallest one is 1 unit of time, while the largest one is 16 units, see Table 1. Figure 2 is a more vivid form of Table 1 by using a histogram.
Figure 1. The ratio jump statistics of HSI’s returns.
Table 1. Frequency statistics of HSI’s jump intervals (Unit of time: 55 min).
3.4. Fitting the Distribution of Jump Intervals
According to the data in Table 1, we use models (1), (2) and (3) to fit the distribution of jump intervals, and get their goodness of fit, see Table 2. When judging the models’ goodness of fit, we usually compare the Adjusted R Square first. The closer to 1, the better. Then we will compare the Sum of Squared Errors (hereafter SSE) and Root Mean Square Error (RMSE). For them, the closer to 0, the better. So seeing from Table 2, it is obvious that the goodness of fit from high to low is the Fokker-Planck distribution, the power law with exponential cutoff and the exponential distribution respectively. Table 3 shows the coefficients and 95% confidence interval of each fit function.
Figure 2. Frequency histogram of HSI’s jump intervals.
Table 2. The fit distributions’ goodness of fit (Unit of time: 55 min).
Table 3. Coefficients’ values of the fit distributions (Unit of time: 55 min).
According to Table 3, we can get the Fokker-Planck distribution:



tegral result is 1 so that it satisfies the nature of probability density function. Similarly, we get the power law with exponential cutoff:


We also get the exponential distribution:


Figure 3 shows the heads and tails of three amended fit distributions. Again, it is obvious that the Fokker-Planck distribution has the best fitting effect. Compared with the exponential distribution, both the Fokker-Planck distribution and the power law with exponential cutoff have the features of the sharp kurtosis and fat tail, which are matched with human behavior dynamics. What’s more, the Fokker-Planck distribution give a higher probability to the tail than the power law with exponential cutoff, and it is also much higher than the exponential distribution.
4. Conclusion
This paper focuses on the counting process N(t) of Kou’s asymmetric double exponential jump-diffusion model [3] . We use the exponential distribution, the Fokker-Planck distribution and the power law with exponential cutoff to fit the distribution of jump intervals after using BNS [9] nonparametric method to detect jumps in 5 min closing data of HIS. It shows that the Fokker-Planck distribution is more suitable in describing the distribution of stock jump intervals, rather than the traditional exponential distribution. So by amending the counting process N(t) into the Fokker-Planck distribution, i.e. amending the asymmetric double exponential jump-diffusion model into the jump
Figure 3. The heads (left hand side) and tails (right hand side) of three amended fit distributions.
diffusion model of power law, it can portray the phenomenon of stock price movement more precisely that has intensive occurrence of jumps, and meanwhile allow the disappearance of jumps over an extended period. This amendment comes into line with the general statistical law of human activities. As the result of this paper, on the one hand, the new “anomaly phenomena” is given out for the already study; on the other hand, human dynamics is introduced into financial mathematical modeling.
Acknowledgements
The research is supported by National Natural Science Foundation of China (No. 71371200 and No. 71071168) and Fundamental Research Funds for the Central Universities (No. 31650017).
Cite this paper
Cao, H.D., Li, Y., He, H.P. and He, Z. (2016) Jump Intervals of Stock Price Have Power-Law Distribution: An Empirical Study. Journal of Mathematical Finance, 6, 770-777. http://dx.doi.org/10.4236/jmf.2016.65053
References
- 1. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654.
http://dx.doi.org/10.1086/260062 - 2. Merton, R.C. (1976) Option Pricing when Underlying Stock Returns Are Discontinuous. Journal of Financial Economics, 3, 125-144.
http://dx.doi.org/10.1016/0304-405X(76)90022-2 - 3. Kou, S.G. (2002) A Jump-Diffusion Model for Option Pricing. Management Science, 48, 1086-1101.
http://dx.doi.org/10.1287/mnsc.48.8.1086.166 - 4. Barabási, A.-L. (2005) The Origin of Bursts and Heavy Tails in Human Dynamics. Nature, 435, 207-211.
http://dx.doi.org/10.1038/nature03459 - 5. Vazquez, A. (2007) Impact of Memory on Human Dynamics. Physic A: Statistical Mechanics and Its Applications, 373, 747-752.
http://dx.doi.org/10.1016/j.physa.2006.04.060 - 6. Vazquez, A., Rácz, B., Lukács, A. and Barabási, A.-.L. (2007) Impact of Non-Poissonian Activity Patterns on Spreading Processes. Physical Review Letters, 98, 158702.
http://dx.doi.org/10.1103/physrevlett.98.158702 - 7. Cao, H.-D., Li, Y. and He, Z. (2011) Stock Pricing Model: Jump Diffusion Model of Power law. Journal of Management Sciences in China, 14, 46-59.
- 8. Barndorff-Nielsen, O.E. and Shephard, N. (2006) Econometrics of Testing for Jumps in Financial Economics Using Bipower Variation. Journal of Financial Economics, 4, 1-30.
- 9. Barndorff-Nielsen, O.E. and Shephard, N. (2004) Power and Bipower Variation with Stochastic Volatility and Jumps. Journal of Financial Economics, 2, 1-37.
http://dx.doi.org/10.1093/jjfinec/nbh001






