Journal of Mathematical Finance
Vol.06 No.01(2016), Article ID:63481,7 pages
10.4236/jmf.2016.61006
Liquidity Management at the Zero Lower Bound and an Era of Activism in Central Banking
Bodo Herzog1,2,3
1Department of Mathematics, ESB Business School, Reutlingen, Germany
2Institute of Finance and Economics, ESB Business School, Reutlingen, Germany
3RRI-Reutlingen Research Institute, Reutlingen University, Reutlingen, Germany

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 October 2015; accepted 14 February 2016; published 17 February 2016
ABSTRACT
The paper studies liquidity management in the banking sector at the zero lower bound implemented by central banks. The new era of monetary policy with interest rates at zero and quantitative easing programs raise questions about the effectiveness of central banking policy and their impact on the banking sector. I find that the zero lower bound reduces liquidity reserves of banks and thus creates less credit supply. The T-LTRO program, developed by the European Central Bank, has helped to tackle this problem. However, the recently expanded asset purchase program reveals the opposite effect. Hence, the recent liquidity provisions by central banks have put incentives rather on de-leveraging than bank lending.
Keywords:
Liquidity Management, Money Supply, Monetary Activism, Central Banking

1. Introduction
Since the Great Credit Crisis of 2007 to 2009, central banks around the world have cut interest rates to the zero lower bound and enforced unconventional monetary policy measures, such as unprecedented open market operations and quantitative easing programs. This new era of monetary policy activism creates new challenges for the liquidity management in the banking sector. The following paper studies liquidity management in both “normal times” and the “Great Credit Crisis” (GCC).
I develop a model and study the zero lower bound policy of central banks and its impact on the banking sector. The zero lower bound policy is defined as nominal interest rates at or close to zero. This monetary policy stance is also labelled highly accommodative or a regime of monetary activism. In this environment both banks and households have incentives to invest or hold cash. However, if the environment is linked to a weak economy and a confidence crisis, deposits are primarily used for debt repayment, i.e. de-leveraging. Thus, the ultimate goal to stabilize the real economy through low interest rates and additional liquidity provisions (i.e. quantitative easing) is significantly constrained by its own mean.
Looking at current global liquidity conditions in financial markets, you find plenty of cheap money all around the world. Nevertheless, the bulk of liquidity provisions have not sufficiently stimulated the economy or bank lending so far. Most of the central bank liquidity is probably simply used to lower the existing debt burden. Hence, targeted liquidity provisions by central banks, such as “Targeted Long-Term Refinancing Operations” (T-LTROs), may help to tackle the current problem during the era of zero lower bound policy or the regime of monetary activism.
The rest of the paper is structured as follows. In Section 2, I give a brief review of the related literature. The model is introduced and discussed in Section 3. I prove two lemmata and theorems. Finally, Section 4 concludes the main findings.
2. Literature Review
The GCC of 2007 to 2009 has demonstrated the importance of the interplay between the financial and real sector. There are many unsolved questions in the macroeconomic debate of today. Of course, seminal papers by [1] -[3] studied some of these linkages in the macro economy. These papers analyze financial frictions in infinite horizon models and make use of log-linear approximations. However, they can only study the effects of financial frictions near the steady state due to the equilibrium approximations and they lag the microeconomic modeling of liquidity management in the banking sector. This paper attempts to close this gap.
Despite obvious caveat this literature has been widely used to study the impact of monetary policy [4] -[6] . The common findings are as follows: temporary shocks have persistent effects on economic activity and finan- cial frictions. In the end, this leads to the amplification of shocks. Consequently, even small financial shocks might have huge effects on the real sector. A new line of continuous time macro-models with non-linearities was established by [7] . They calibrate the model and show that in times of crisis, equity injection is a superior policy compared to interest rate cuts or asset-purchasing programs by the central bank. Due to the fact that the extent and length of slumps are stochastic, [7] find a significant increase of the amplification and persistence of adverse shocks. In the end, this creates a constellation in which the system is trapped in a recession with low growth and a misallocation of resources for some time. This is an important insight for central banks and my paper follows this line of research.
There is some literature about the optimal allocation of bank liquidity. The work by [8] -[10] show two important aspects relevant to my paper. First, the limited participation implies that assets offered for sale in the market will not attract bids from all possible buyers and thus a lower sale price can be anticipated. As a con- sequence, they show that banks can emerge endogenously to solve the liquidity problem generated by limited participation. In addition, the contribution by [9] studies directly the liquidity demand by firms. They show interesting results related to my findings. But the model shares a fundamental element with [11] that banks provide insurance against liquidity shocks which is a restrictive assumption and relaxed in my paper. However, the demand for this insurance does not come from the risk aversion of depositors because depositors are risk- neutral [9] .
A further aspect is studied by [12] in the banking literature. They argue that a bilateral bank-borrower relationship may be superior to multilateral lending. Similar arguments are modeled along the same lines by [13] [14] . Finally, [15] find a new explanation for traditional deposit taking and lending in banking due to economies of scales. They argue that the liquidity reserves held by banks can also be used as a buffer against the risk that firms draw on their credit lines. Moreover, they show that banks with large amounts of deposits are more likely to offer loan commitments.
Our model sets itself apart from the existing banking literature: Firstly, I setup an optimal allocation and liquidity cost function in normal times and under market distress. Secondly, I study this tractable model in respect of liquidity management at the zero lower bound. Moreover, I study the effectiveness or ineffectiveness of new monetary policy measures in the macroeconomic money supply and demand framework. Finally, I analyze the impact of unconventional monetary policy measures, such as extended liquidity provisions or quantitative easing programs.
3. Model and Discussion
The model consists of two parts: 1) the microeconomic modeling of expected liquidity demand by banks, and 2) the macroeconomic equilibrium of money supply, provided by the central bank, and money demand in the banking sector.
Let me first develop the microeconomic model of expected liquidity demand. I create a standard liquidity cost function in banking under fixed costs and open market operations implemented by a central bank. I assume that every commercial bank has to hold required or mandatory liquidity/reservers,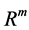 . This assumption is standard and does reflect reality in central banking. The mandatory reservers help to guarantee financial and macroe- conomic stability. Hence, central banks change
. This assumption is standard and does reflect reality in central banking. The mandatory reservers help to guarantee financial and macroe- conomic stability. Hence, central banks change 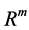 over time correspondingly. Moreover, banks hold further reservers (
over time correspondingly. Moreover, banks hold further reservers (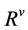 ) as a buffer against shocks, according to Basel III regulation or according to their investment strategy. These regulatory reservers change over time and must be determined. Of course, the usually expected liquidity needs, X, are greater than
) as a buffer against shocks, according to Basel III regulation or according to their investment strategy. These regulatory reservers change over time and must be determined. Of course, the usually expected liquidity needs, X, are greater than 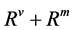 and the additional money is either obtained by open market operations from the central bank or the interbank market. However, both sources of additional liquidity are uncertain in quantity,
and the additional money is either obtained by open market operations from the central bank or the interbank market. However, both sources of additional liquidity are uncertain in quantity, 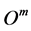 , and price,
, and price,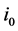 . Consequently, price and quantity and thus X are stochastic variables.
. Consequently, price and quantity and thus X are stochastic variables.
Figure 1 illustrates the liquidity cost function if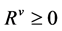 . Note the assumption of
. Note the assumption of  is a graphical simplification. In the analytical discussion, I differentiate between positive and negative liquidity reserves. Furthermore, note that the interest rates vary across different segments of the liquidity cost function due to different monetary policy operations, such as central bank lending and borrowing facilities, further refinancing operations, or quantitative easing programs.
is a graphical simplification. In the analytical discussion, I differentiate between positive and negative liquidity reserves. Furthermore, note that the interest rates vary across different segments of the liquidity cost function due to different monetary policy operations, such as central bank lending and borrowing facilities, further refinancing operations, or quantitative easing programs.
Throughout the paper, 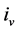 is the interest rate on the reserve holdings’ due to regulatory requirements and
is the interest rate on the reserve holdings’ due to regulatory requirements and 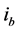 is the borrowing interest rate via the central bank lending facility. This lending facility is accessible at any time and therefore the most expansive source of financing for banks. The amount of open market operations is denoted by
is the borrowing interest rate via the central bank lending facility. This lending facility is accessible at any time and therefore the most expansive source of financing for banks. The amount of open market operations is denoted by 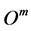 and the respective interest rate by
and the respective interest rate by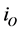 ; both parameters are stochastic.
; both parameters are stochastic.
Figure 1. Liquidity cost function if .
.
In general, the current liquidity demand, X, by banks is a random variable. I assume that X has a standard rectangular probability distribution. The probability distribution is represented by
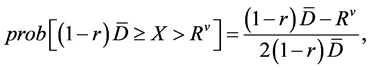 (1)
(1)
where 
function with respect to the (random) reserve holding 

central banks or the interbank market is involved with transaction costs. I model the transaction costs by a fixed parameter c. According to Figure 1, I obtain for 

where again 










The optimal liquidity reserve, 



Secondly, marginal revenues in the banking sector is given by



Solving the last line for 


where
Lemma 1. The optimal reserve holding 


Proof. The computation of both partial derivatives 

Both signs are as expected because the standard borrowing rate (so-called lending facility in central banking) is always greater than both the deposit rate (i.e.

Lemma 2. At the zero lower bound, optimal reserve holding 


Proof. Using Lemma (1), I demonstrate that at the zero lower bound the negative relationship is even greater
because the denominator is greater:


lower bound. □
Obviously, during crises the central bank intends to stimulate the economy by lowering the interest rates. According to the economic rational banks should use the excess of cheap liquidity to disburse more credit for new and productive investments. However, whether banks follow this behaviour depends on several factors, such as the banks’ debt levels or the expected economic development. To study this problem in more detail, I setup a simple macro-model of money supply and demand in the next subsection.
Money Supply and Demand: Macroeconomic View
In this Section, I introduce an aggregate money market model. Money supply is determined by the central bank and money demand is determined by banks in the banking and household sector. The microeconomic foundation of money demand is already developed above. The households hold deposits in three different forms:
1) Cash defined as
2) Short-term saving defined as
3) Saving defined as
Thus, the banks have total equity 






where K is the total credit supply to businesses and households. The overall economy has an equilibrium if money supply is equal to money demand. This is given by

Theorem 1. Monetary policy at the zero lower bound increases money supply 


Proof. First, I show that “normal” money supply 

Hence, I obtain an “extended money supply” defined as 


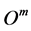



Theorem 2. Unconditional monetary policy measures at the zero lower bound are ineffective.
Proof. Theorem 1 demonstrates that cash holding will increase during a period of interest rates at the zero lower bound. This implies due to Equation (7) that for given 

Therefore, the European Central Bank (ECB) has developed a modified long-term open market operation, a so-called “targeted long-term refinancing operation” (T-LTRO). This tool provides cheap liquidity to private banks if and only if the money from the central bank is forwarded to businesses and households [16] .1 This conditionality creates an effective monetary policy measure at the zero lower bound. Hence, the central bank is able to circumvent the ineffectiveness of unconditional liquidity provisions (Theorem 2). Nevertheless, the ECB provides also unconditional liquidity of 60 bn Euro per month by the new extended asset purchasing program (quantitative easing, QE) since March 2015 to end September 2016. In fact, the QE program might be counter- productive because of Theorem 2. Moreover, in practise the ECB has put a negative deposit rate of −0.25 percent in place which mitigates deposit holdings even further. Hence under current conditions, the most effec- tive use of cash and additional liquidity is de-leveraging.
4. Conclusions
In this paper I have studied the impact of liquidity management in banking under the regime of central bank activism, defined as a zero lower bound policy and massive liquidity injections via quantitative easing programs. It turns out that those liquidity provisions by central banks, especially unconditional liquidity, are partly detrimental to stabilize the economy.
The economic rational of this proposition is simple: The zero lower bound policy is lowering reserve holding in the banking sector. Thus, banks and households have incentives to increase cash holdings. Hence, money on a saving account is primarily used for debt repayment, i.e. de-leveraging. Consequently, the ultimate goal to stabilize the real economy by interest rates at the zero lower bound or quantitative easing programs has been not fully achieved. On the contrary, the model demonstrates that the additional liquidity more likely lowers the debt burden than stimualtes the economy. I indirectly confirm that targeted liquidity provisions, such as “Targeted Long-Term Refinancing Operations” (T-LTROs) might be more effective in particular during the era of zero lower bound policy. Consequently, un-targeted liquidity provisions are more or less ineffective in an era of monetary activism.
Acknowledgements
I thank the Editor and the two anonymous referees for their comments. Research is funded by the Reutlingen Research Institute. This support is greatly appreciated.
Cite this paper
BodoHerzog,11,11, (2016) Liquidity Management at the Zero Lower Bound and an Era of Activism in Central Banking. Journal of Mathematical Finance,06,48-54. doi: 10.4236/jmf.2016.61006
References
- 1. Bernanke, B. and Gertler, M. (1989) Agency Costs, Net Worth, and Business Fluctuations. American Economic Review, 79, 14-31.
- 2. Kiyotaki, N. and Moore, J. (1997) Credit Cycles. Journal of Political Economy, 105, 211-248.
http://dx.doi.org/10.1086/262072 - 3. Bernanke, B., Gertler, M. and Gilchrist, S. (1999) The Financial Accelerator in a Quantitative Business Cycle Framework. Handbook of Macroeconomics, 1, 1341-1393.
http://dx.doi.org/10.1016/S1574-0048(99)10034-X - 4. Woodford, M. (2010) Robustly Optimal Monetary Policy with Near-Rational Expectations. American Economic Review, 100, 274-303.
http://dx.doi.org/10.1257/aer.100.1.274 - 5. Gertler, M. and Kiyotaki, N. (2011) Financial Intermediation and Credit Policy in Business Cycle Analysis. In: Woodford, M. and Friedman, B.M., Eds., Handbook of Monetary Economics, Elsevier.
- 6. Brunnermeier, M., Eisenbach, T. and Sannikov, Y. (2012) Macroeconomics with Financial Frictions: A Survey. In: Acemoglu, D., Arellano, M. and Dekel, E., Eds., Advances in Economics and Econometrics: Tenth World Congress of the Econometric Society, Cambridge University Press, Vol. 2, 3-94.
- 7. Brunnermeier, M.K. and Sannikov, Y. (2014) A Macroeconomic Model with a Financial Sector. American Economic Review, 104, 379-421.
http://dx.doi.org/10.1257/aer.104.2.379 - 8. Diamond, D.W. (1997) Liquidity, Banks, and Markets. Journal of Political Economy, 105, 928-956.
http://dx.doi.org/10.1086/262099 - 9. Holmström, B. and Tirole, J. (1998) Private and Public Supply of Liquidity. Journal of Political Economy, 106, 1-40.
http://dx.doi.org/10.1086/250001 - 10. Freixas, X. and Jorge, J. (2008) The Role of Interbank Markets in Monetary Policy: A Model with Rationing. Journal of Money, Credit and Banking, 40, 1151-1176.
http://dx.doi.org/10.1111/j.1538-4616.2008.00152.x - 11. Diamond, D.W. and Dybvig, P. (1983) Bank Runs, Deposit Insurance, and Liquidity. Journal of Political Economy, 91, 401-419.
http://dx.doi.org/10.1086/261155 - 12. Bhattacharya, S. and Chiesa, G. (1995) Proprietary Information, Financial Intermediation and Research Incentives. Journal of Financial Intermediation, 4, 328-357.
http://dx.doi.org/10.1006/jfin.1995.1014 - 13. Yosha, O. (1995) Information Disclosure Costs and the Choice of Financing Source. Journal of Financial Intermediation, 4, 3-20.
http://dx.doi.org/10.1006/jfin.1995.1001 - 14. Yosha, O. (1995) Arm’s Length Financing and Competition in Product Markets: A Welfare Analysis. Discussion Paper, Tel Avivi University, Israel.
- 15. Kashyap, A., Rajan, R. and Stein, J. (1999) Banks as Liquidity Providers: An Explanation for the Co-Existence of Lending and Deposit Taking. Discussion Paper, SSN 156748.
http://dx.doi.org/10.2139/ssrn.156748 - 16. Martin, A. (2009) Reconciling Bagehot and the Fed’s Response to September 11. Journal of Money, Credit, and Banking, 41, 397-415.
http://dx.doi.org/10.1111/j.1538-4616.2009.00210.x
NOTES
1Excluding loans for house purchase.






