Journal of Mathematical Finance
Vol.04 No.05(2014), Article ID:51818,12 pages
10.4236/jmf.2014.45033
Continuous-Time Mean-Variance Portfolio Selection with Partial Information
Wan-Kai Pang1, Yuan-Hua Ni2, Xun Li1, Ka-Fai Cedric Yiu1
1Department of Applied Mathematics, The Hong Kong Polytechnic University, Hong Kong, China
2School of Sciences, Tianjin Polytechnic University, Tianjin, China
Email: macyiu@polyu.edu.hk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2014; revised 1 October 2014; accepted 21 October 2014
ABSTRACT
This paper studies a continuous-time market under a stochastic environment where an agent, having specified an investment horizon and a target terminal mean return, seeks to minimize the variance of the return with multiple stocks and a bond. In the model considered here, the mean returns of individual assets are explicitly affected by underlying Gaussian economic factors. Using past and present information of the asset prices, a partial-information stochastic optimal control problem with random coefficients is formulated. Here, the partial information is due to the fact that the economic factors can not be directly observed. Using dynamic programming theory, we show that the optimal portfolio strategy can be constructed by solving a deterministic forward Riccati-type ordinary differential equation and two linear deterministic backward ordinary differential equations.
Keywords:
Mean-Variance Portfolio Selection, Partial Information, Filtering

1. Introduction
Mean-variance is an important investment decision rule in financial portfolio selection, which is first proposed and solved in the single-period setting by Markowitz in his Nobel-Prize-winning works [1] [2] . In these seminal papers, the variance of the final wealth is used as a measure of the risk associated with the portfolio and the agent seeks to minimize the risk of his investment subject to a given mean return. This model becomes the foundation of modern finance theory and inspires hundreds of extension and applications. For example, this leads to the elegant capital asset pricing model [3] .
The dynamic extension of the Markowitz model has been established in subsequent years by employing the martingale theory, convex duality and stochastic control. The pioneer work for continuous time portfolio management is [4] , in which Merton used dynamic programming and partial differential equation (PDE) theory to derive and solve the Hamilton-Jacobi-Bellman (HJB) equation, and thus obtains the optimal strategy. For cases when the underlying stochastic process is a Martingale, optimal portfolios could be derived [5] . In [6] , the authors formulated the mean-variance problem with deterministic coefficients as a linear-quadratic (LQ) optimal problem. As there is no running cost in the objective function, this formulation is inherently an indefinite stochastic LQ control problem. As extensions of [6] , for example, [7] dealt with random coefficients, while [8] considered regime switching market. For discrete time cases, [9] solved the multiperiod mean-variance portfolio selection problem completely. Analytical optimal strategy and an efficient algorithm to find the strategy were proposed. Comprehensive review of the mean-variance model can be found in [10] and [11] .
In [12] , in order to tackle the computational tractability and the statistical difficulties associated with the estimation of model parameters, Bielecki and Pliska introduced a model such that the underlying economic factors such as accounting ratios, dividend yields, and macroeconomic measures are explicitly incorporated in the model. The factors are assumed to follow Gaussian processes and the drifts of the stocks are linear functions of these factors. This model motivates many further researches (see, for example, [13] and [14] ). In practice, many investors use only the observed asset prices to decide his current portfolio strategy. The random factors cannot normally be observable directly. Therefore, the underlying problem falls into the category of portfolio selection under partial information [15] [16] . A significant progress in the realm of mean-variance concerning partial information is the work of [17] , in which a separation principle is shown under this partial information setting. Efficient strategies were derived, which involved the optimal filter of the stock drift processes. In addition, the particle system representation of the obtained filter is employed to develop analytical and numerical approaches. It is valuable to point out that backward stochastic differential equations (BSDEs) methodology is employed to tackle this problem.
This paper attempts to deal with the mean-variance portfolio selection under partial information based on the model of [12] . By exploiting the properties of the filtering process and the wealth process, we tackle this problem directly by the dynamic programming approach. We show that optimal strategy can be constructed by solving a deterministic forward Riccati-type ordinary differential equation (ODE) and a system of linear deterministic backward ODEs. Clearly, by reversing the time, a deterministic backward ODE can be converted to a forward one. Therefore, we can easily derive the analytic solutions of the ODEs, and thus the analytic form of the optimal strategies. This is the main contribution of the paper. The proposed procedure is different from that of [17] , where BSDEs are employed.
The rest of the paper is organized as follows. In Section 2, we formulate the mean-variance portfolio selection model under partial information, and an auxiliary problem is introduced. Section 3 gives the optimal strategy of the auxiliary problem by the dynamic programming method. Section 4 studies the original problem, while Section 5 gives some concluding remarks.
2. Mean-Variance Model
Throughout this paper 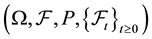 is a fixed filtered complete probability space on which a standard
is a fixed filtered complete probability space on which a standard  - adapted
- adapted  -dimensional Brownian motion
-dimensional Brownian motion 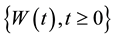 is defined, where
is defined, where 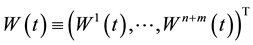 and
and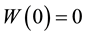 . Let
. Let 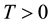 be the terminal time of an investment, and
be the terminal time of an investment, and 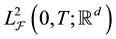 denotes the set of all
denotes the set of all 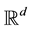 -valued,
-valued, 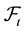 -adapted stochastic processes
-adapted stochastic processes 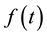 with
with 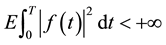 ; similarly
; similarly  can be defined for any functions with domain in
can be defined for any functions with domain in  and filtration
and filtration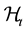 .
.
There is a capital market containing  basic securities (or assets) and
basic securities (or assets) and 



where 




where



and the factors are Gaussian processes. To be precise, denoting 

where the constant matrices 



Consider an agent with an initial endowment 





where




Let
As pointed out by [17] , practically, the investor can only observe the prices of assets. So, at time



Definition 2.1. A portfolio 




The agent’s objective is to find an admissible portfolio



is minimized. The problem of finding such a portfolio 
Definition 2.2. The mean-variance portfolio selection problem, with respect to the initial wealth
mulated as a constrained stochastic optimization problem parameterized by

The problem is called feasible (with respect to





We impose the basic assumption:
Assumption (PD). For any

Let
with 


By the definition of



By Itô’s formula we have
Define

then 


By (2.7), a simple calculation shows that

Substituting (2.9), we have an equivalent representation of the wealth process

where

This is the separation principle developed by [17] , which enables us to solve problem (2.5) as if the drifts 


By general convex optimization theory, the constrained optimal problem (12) with 



which is equivalent to the following (denoting 



in the sense that two problems have exactly the same optimal strategy. In the following, we will call problem (2.14) the auxiliary problem of the original problem (2.12).
3. Optimal Policy for the Auxiliary Problem
The problem (2.14) can be viewed as an unconstrained special stochastic optimal control problem with random coefficients in system equation and zero integral term in the performance index. Different from existing results using BSDEs methodology, in this section, we derive the optimal portfolio strategy from dynamic programming directly. This enables us to derive the optimal policy by solving just two linear deterministic backward ODEs and a Riccati-type forward deterministic ODE.
3.1. Analysis of Hamilton-Jacobi-Bellman Equation
Let 



where 


To evaluate
By Itô’s formula, it follows that
where 








which makes 

In this and the following PDEs and ODEs, the arguments 
Noticing that the terminal condition of 


Simple calculation shows
Substituting 

By the special structure of (3.5), the following separation form of 

which will be proved in Theorem 3.1. Therefore, the optimal control (3.2) has the following structure
which is linear in

Clearly, if 

then 
3.2. Optimal Policy
Notice that the left hand side of the first equation in (3.8) is linear in






with











Theorem 3.1. For problem (2.14), the optimal strategy is given by

where




Proof. Bearing the form (3.9) of 
Therefore, (3.8) is equivalent to

which is equivalent to
(3.14)
The left hand of above PDE can be decomposed into three terms:
1) the term that is irrespective of
2) the term that is linear in
3) the term that is quadratic in
So, if the 



we can determine the function



Thus, 


by innovation process 


completes the proof.
We will give a brief discussion about the solvability in theory of (2.8) (3.11) (3.12). Clearly, 
with


with

where

Therefore,
Clearly, (3.12) is a Lyapunov differential equation, which is solved by introducing the following operator
where 


where
Let

Therefore,
where 

4. Efficient Frontier
In this section, we proceed to derive the efficient frontier for the original portfolio selection problem under partial information. To begin with, we prove a lemma which shows the feasibility of the original problem.
Lemma 4.1. Problem (5) is feasible, and the minimal mean-variance of the terminal wealth process is finite.
Proof. The proof follows directly from results of Section 5 in [17] . In the language of [17] , (2.10) can be rewritten as

where 

Clearly, 





Now, we state our main theorem.
Theorem 4.1. The efficient strategy of Problem (2.5) with the terminal expected wealth constraint 

Here, 



where 

and


Proof. By Lemma 4.1, we know that the constraint Problem (2.5) is feasible, and its minimal terminal mean- variance 

where the equality is true by general convex constraint optimization theory (see, for example, [22] ). By Theorem 3.1, the wealth Equation (2.10) evolves as
In terms of
Clearly,
Thus
where 
For any fixed

To obtain the optimal mean-variance value and the optimal portfolio strategy of Problem (2.5), we should maximize (4.6) over 



And we can assert that
If this is not true, the optimal cost will be infinite, which contradicts (4.5).
5. Conclusion
In this paper, we have studied the continuous-time mean-variance portfolio selection problem with stochastic drifts. In particular, drifts are assumed to be linear functions of economic factor processes. Because the factor processes cannot be observed directly, partial information is assumed together with a filter process. Conse- quently, by dynamic programming technique and the method of separation of variables, we have derived the explicit optimal strategy via the solution of a system of ODEs. As a future extension, it would be of interest to study the solutions with real financial data and carry out appropriate economic analysis. Also, regime-switching model [23] and the scenario for no-bankruptcy can also be considered.
Acknowledgements
This work is supported by the PolyU grant G-YL05 and A-PL62, and the JRI of the Department of Applied Mathematics, The Hong Kong Polytechnic University.
Cite this paper
Wan-KaiPang,Yuan-HuaNi,XunLi,Ka-Fai CedricYiu, (2014) Continuous-Time Mean-Variance Portfolio Selection with Partial Information. Journal of Mathematical Finance,04,353-365. doi: 10.4236/jmf.2014.45033
References
- 1. Markowitz, H. (1952) Portfolio Selection. Journal of Finance, 7, 77-91.
- 2. Markowitz, H. (1959) Portfolio Selection: Efficient Diversification of Investment. John Wiley & Sons, New York.
- 3. Sharpe, W.F. (1964) Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance, 19, 425-442.
- 4. Merton, R. (1971) Optimum Consumption and Portfolio Rules in a Continuous Time Model. Journal of Economic Theory, 3, 373-413.
http://dx.doi.org/10.1016/0022-0531(71)90038-X - 5. Pliska, S.R. (1986) A Stochastic Calculus Model of Continuous Trading: Optimal Portfolios. Mathematics of Operations Research, 11, 371-384.
http://dx.doi.org/10.1287/moor.11.2.371 - 6. Zhou, X.Y. and Li, D. (2000) Continuous-Time Mean-Variance Portfolio Selection: A Stochastic LQ Framework. Applied Mathematics and Optimization, 42, 19-33.
http://dx.doi.org/10.1007/s002450010003 - 7. Lim, A.E.B. and Zhou, X.Y. (2002) Mean-Variance Portfolio Selection with Random Parameters in a Complete Market. Mathematics of Operations Research, 27, 101-120.
http://dx.doi.org/10.1287/moor.27.1.101.337 - 8. Zhou, X.Y. and Yin, G. (2003) Markowitz’s Mean-Variance Portfolio Selection with Regime Switching: A Continuous Time Model. SIAM Journal on Control and Optimization, 42, 1466-1482.
http://dx.doi.org/10.1137/S0363012902405583 - 9. Li, D. and Ng, W.L. (2000) Optimal Dynamic Portfolio Selection: Multi-Period Mean-Variance Formulation. Mathematical Finance, 10, 387-406.
http://dx.doi.org/10.1111/1467-9965.00100 - 10. Steinbach, M.C. (2001) Markowitz Revisited: Mean-Variance Models in Financial Portfolio Analysis. SIAM Review, 43, 31-85.
http://dx.doi.org/10.1137/S0036144500376650 - 11. Bielecki, T.R., Jin, H., Pliska, S.R. and Zhou, X.Y. (2005) Continuous-Time Mean-Variance Portfolio Selection with Bankruptcy Prohibition. Mathematical Finance, 15, 213-244.
http://dx.doi.org/10.1111/j.0960-1627.2005.00218.x - 12. Bielecki, T.R. and Pliska, S.R. (1999) Risk-Sensitive Dynamic Asset Management. Applied Mathematics and Optimization, 39, 337-360.
http://dx.doi.org/10.1007/s002459900110 - 13. Nagai, H. and Peng, S.G. (2002) Risk-Sensitive Dynamic Portfolio Optimization with Partial Information on Infinite Time Horizon. The Annals of Applied Probability, 12, 173-195.
http://dx.doi.org/10.1214/aoap/1015961160 - 14. Bielecki, T.R. and Pliska, S.R. (2004) Risk-Sensitive ICAPM with Application to Fixed-Income Management. IEEE Transactions on Automatic Control, 49, 420-432.
http://dx.doi.org/10.1109/TAC.2004.824470 - 15. Lakner, P. (1995) Utility Maximization with Partial Information. Stochastic Processes and Their Applications, 56, 247273.
http://dx.doi.org/10.1016/0304-4149(94)00073-3 - 16. Lakner, P. (1998) Optimal Trading Strategy for an Investor: The Case of Partial Information. Stochastic Processes and Their Applications, 76, 77-97.
http://dx.doi.org/10.1016/S0304-4149(98)00032-5 - 17. Xiong, J. and Zhou, X.Y. (2007) Mean-Variance Portfolio Selection under Partial Information. SIAM Journal on Control and Optimization, 46, 156-175.
http://dx.doi.org/10.1137/050641132 - 18. Karatzas, I. and Shreve, S.E. (1991) Methods of Mathematical Finance. Springer-Verlag, New York.
- 19. Li, X. and Zhou, X.Y. (2006) Continuous-Time Mean-Variance Efficiency: The 80% Rule. Annals of Applied Probability, 16, 1751-1763.
http://dx.doi.org/10.1214/105051606000000349 - 20. Liptser, R.S. and Shiryaev, A.N. (2001) Statistics of Random Processes: I. General Theory. Springer, Berlin.
- 21. Kallianpur, G. (1980) Stochastic Filtering Theory. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4757-6592-2 - 22. Luenberger, D.G. (1968) Optimization by Vector Space Method. John Wiley, New York.
- 23. Yiu, K.F.C., Liu, J.Z., Siu, T.K. and Ching, W.K. (2010) Optimal Portfolios with Regime-Switching and Value-at-Risk Constraint. Automatica, 46, 979-989.
http://dx.doi.org/10.1016/j.automatica.2010.02.027







































