Journal of Mathematical Finance
Vol.04 No.03(2014), Article ID:46379,12 pages
10.4236/jmf.2014.43018
A New range-Based Regime-switching Dynamic conditionalcorrelation Model for Minimum-variance hedging
Yi-Kai Su1*, Chun-Chou Wu2
1Graduate Institute of Finance, National Taiwan University of Science and Technology, Taiwan
2Department of Finance, National Kaohsiung First University of Science and Technology, Taiwan
Email: *jerrysu89540551@gmail.com, wucc123@seed.net.tw
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2014; revised 7 April 2014; accepted 7 May 2014
ABSTRACT
This study proposes a new range-based Markov-switching dynamic conditional correlation (MS- DCC) model for estimating the minimum-variance hedging ratio and comparing its hedging per- formance with that of alternative conventional hedging models, including the naïve, OLS regres- sion, return-based DCC, range-based DCC and return-based MS-DCC models. The empirical results show that the embedded Markov-switching adjustment in the range-based DCC model can clearly delineate uncertain exogenous shocks and make the estimated correlation process more in line with reality. Overall, in-sample and out-of sample tests indicate that the range-based MS-DCC model outperforms other static and dynamic hedging models.
Keywords:
minimum-variance hedge Ratio, Markov-Switching, correlation, range-Based DCC Model, Regime shift

1. Introduction
The dynamic conditional correlation (DCC) model, the celebrated multivariate correlation estimation model proposed by Engle [1] , solves the requirement of a positive definite constraint in parameter estimation, the abil- ity to estimate many parameters and time-varying correlation1. The DCC model also provides some advantages through its operating procedure, which enables more parsimonious parameter estimation and easy estimation. Drawing on related literatures, the current models of correlation estimation were developed to extract return data to estimate covariance processes. A few recent studies have attempted to introduce a range variable to replace the return variable for more information content and to account for efficient market theory. More information can be gathered with a range structure than with a return variable when estimating a volatility model for many separate empirical results2. For example, Chou et al. [12] construct a range-based DCC model and propose that their model setting outperforms the original return-based DCC model in estimating and forecasting covariance matrices. Al- though the return- and range-based DCC models feature many advantages in correlation process fitting, they still place several constraints on linear parameters for covariance and correlation equations3. It is natural to introduce a nonlinear mechanism into the return- and range-based DCC models to enhance feasibility. In this study, we pro- pose a new range-based regime-switching DCC model that is able to enhance the hedge effect in futures markets.
Conventional approaches to nonlinear adjustment among financial time-series models include threshold auto- regressive techniques, smooth transition and Markov-switching. We introduce the Markov-switching method proposed by Hamilton [15] [16] to extend the original DCC structure. One advantage of the Markov-switching method is that it treats the regime shift as an exogenous variable. Simplifying the formidable task of statistical estimation, the Markov-switching structure can be applied from the mean to variance and covariance equations. The combination Markov-switching and volatility model is able to address volatility processes with greater flexibility through regime-switching. Meanwhile, such a volatility model with Markov-switching can enable the estimated coefficients to change in different states. Drawing on the DCC model of Engle [1] , the extension of a return-based DCC model with regime-switching has been introduced in some studies. For instance, Pelletier [17] and Billio and Caporin [18] propose a variant multivariate GARCH model composed of a Markov chain and the DCC model. These studies consider a solution that a discrete level shift may exist in the dynamic conditional correlation process. Moreover, they verify that the return-based Markov-switching DCC model outperforms En- gle’s [1] single-regime DCC model structure. Because the range-based DCC model is superior to the conven- tional return-based method in depicting the pattern of correlation shown by Chou et al. [12] , it is necessary to explore whether the range correlation model with data structure change remains useful for futures hedging. Ac- cordingly, we construct a Markov chain structure into the range-based DCC model, and compute the mini- mum-variance hedge ratio for comparison with other hedging approaches.
The literature has historically used the utility function and ordinary least squares model to discuss mini- mum-variance hedging. According to Chen et al. [19] and Lien and Tse’s [20] research, advanced econometric models have recently been used to measure the minimum-variance hedge ratio. In other words, the manner of hedging is shifting from static hedging to time-varying hedging. There is a large body of evidence showing that time-varying hedging approaches perform better than the static case4. In contrast, some empirical studies argue that there are no significant improvements from employing advanced econometric techniques5. According to Lien [29] - [31] , the inconsistent performance of such hedging is caused by the abuse of hedging effectiveness measures. This proposal is supported by Ederington [32] . From previous discussions, there remains a difficulty in using advanced econometric tools to measure the hedge ratio. Therefore, this study employs a range-based Markov-switching dynamic conditional correlation (MS-DCC) model to estimate the dynamic hedge ratio and discusses the hedging effectiveness of other approaches.
The rest of this article is organized as follows. In the next section, the range-based regime-switching DCC model is introduced, and minimum-variance hedging is described in the following section. In the fourth section, this study presents a hedging effectiveness measurement. The empirical results and the economic intuition of these results are reported in the fifth section. The final section provides the conclusion.
2. Range-Based Regime-switching Dynamic Conditional correlation model
To introduce the regime-switching structure to the range-based dynamic conditional correlation process, the range-based MS-DCC model with a general S-regime can be expressed as:
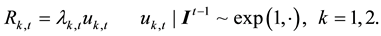 (1a)
(1a)
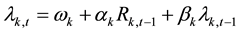 , (1b)
, (1b)
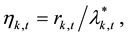 where
where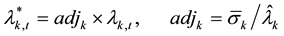 , (1c)
, (1c)
 (1d)
(1d)
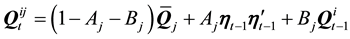 , (1e)
, (1e)
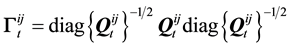 , (1f)
, (1f)
where Equations (1a)-(1c) represent the range-based volatility specification, 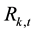 denotes the observed high-low range in the logarithm of the kth asset during the time interval t,
denotes the observed high-low range in the logarithm of the kth asset during the time interval t, 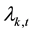 denotes the conditional mean of the range,
denotes the conditional mean of the range,
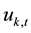 denotes the disturbance term, which follows the exponential distribution with unit mean,
denotes the disturbance term, which follows the exponential distribution with unit mean, 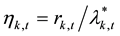 is
is
the standardized residual, and the scaled expected range 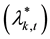 is substituted for the conditional standard devi-
is substituted for the conditional standard devi-
ation. The unconditional standard deviation of the return series k and the sampling mean of the estimated condi-
tional range of the series k are represented as 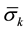 and
and 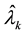 , respectively. The Markov chain transition proba-
, respectively. The Markov chain transition proba-
bility, which has the constraints 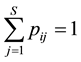 for
for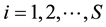 , and
, and 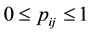
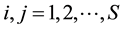
Equation (1d). It is intuitive to define the stationary distribution of the Markov chain as 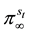
represented as
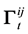
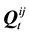
time-varying covariance matrix. In Equations (1e) and (1f), the superscript symbol represents the regime shift from i to j. In short, the range-based MS-DCC model is composed of the conditional autoregressive range (CARR) model for the conditional variance process and the Markov-switching approach for the conditional co- variance and correlation case.
The log likelihood function of the MS-DCC model is presented in this section. According to Engle [1] and Chou et al. [12] , the two-step quasi-maximum likelihood approach is suitable for estimating the models in the DCC family. It is natural to execute the first step quasi-maximum likelihood estimation (QMLE) using Equation (2), as our specification allows only the conditional correlation to change in different regimes. The likelihood function of the volatility component, 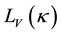
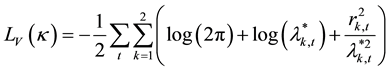
By maximizing the QMLE of Equation (2), the parameters 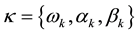
1) given the filtered probabilities as inputs, determine the joint probabilities as:
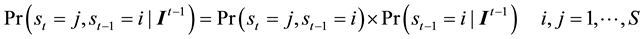
2) evaluate the regime-dependent log likelihood as:
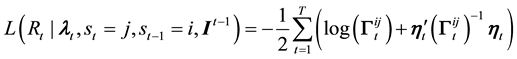
3) evaluate the log likelihood of observation t as:
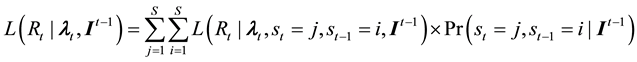
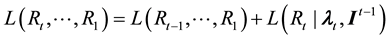
4) renew the joint probabilities as:
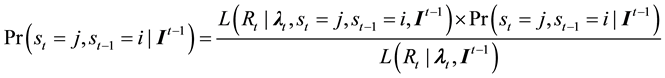
5) calculate the filtered probabilities as:
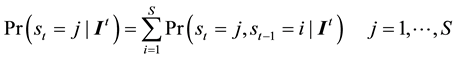
6) renew the dynamic conditional correlation matrix through the following approximation:

7) iterate 1 to 6 until the end of the sample. The unknown parameters of MS-DCC model can be obtained with these estimation procedures.
3. Minimum-variance Hedging
Minimum-variance hedging is the determination of the number of futures contracts against one spot asset that will ensure the minimum variance of the hedging portfolio. Furthermore, minimum-variance hedging can be calculated as a ratio of the covariance of spot-futures returns over the variance of futures returns, namely,
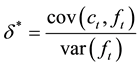
where 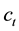
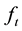
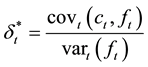
This study selects six various minimum-variance hedge ratios for the time being:
1) Naïve: A simple hedging strategy assigning the hedge ratio equal to −1 at all times.
2) OLS: A conventional method for analyzing the minimum-variance hedge ratio, used by Ederington [32] through the simple OLS regression,
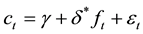
The estimated slope, 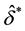
3) Return-based DCC: A classical time-varying correlation model proposed by Engle [1] , which can be shown as:

4) Range-based DCC: A range-based dynamic conditional correlation model developed by Chou et al. [12] , which can be expressed as:
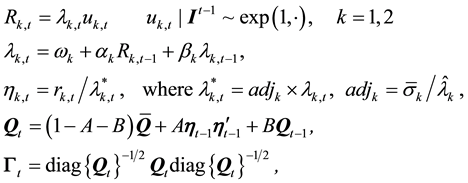
5) Return-based MS-DCC: A more flexible return-based dynamic conditional correlation model proposed by Pelletier [17] and Billio and Caporin [18] , which can be expressed as:
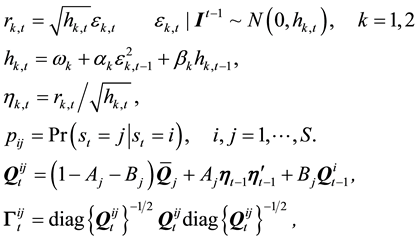
6) Range-based MS-DCC: A range-based dynamic conditional correlation model with a regime-switching structure, which can be expressed as Equations (1a)-(1f).
4. Hedging effectiveness Measure
With regard to the hedging effectiveness measure, this study employs the variance reduction and further calcu- lates the percentage variance reduction. In addition, this study calculates the economic benefits including the expected daily utility and the value-at-risk (VaR) estimate. The investor faces the mean-variance expected daily utility function proposed by Kroner and Sultan [22] , which can be represented as:
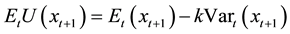
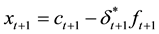
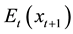
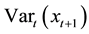
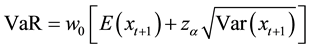
where 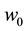
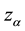
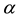
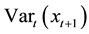
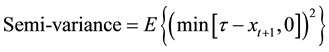
where 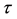
5. Empirical analysis
This study selects two stock indices with different weighting schemes for model testing at this stage, namely, the value-weighted S&P 500 index, the equal-weighted NIKKEI 225 index, and their corresponding futures con- tracts. The sample period is from January 3, 2000 to June 29, 2011 for the empirical study. One goal of this study is to detect using these two different weighted indices whether the range-based MS-DCC model outper- forms competing models. The daily high, low, and close price for the S&P 500 and NIKKEI 225 are obtained from Datastream.
Descriptive statistics for daily returns and ranges data are reported in Table 1. The spot and futures index vo- latilities (standard deviation) for the NIKKEI 225 are larger than those for the S&P 500. This finding is in line with equal-weighted stock indices’ property of having higher volatility than value-weighted indices, as equal- weighted schemes allocate the same weight to each stock, and small-cap stocks are generally more volatile than their large-cap counterparts. Both markets’ return and range data are found to reject the null hypothesis of nor- mal distribution by the Bera-Jarque criterion. Here, the Bera-Jarque statistics are greater than the chi-squared value with a degree of freedom of 2. Furthermore, the kurtosis test for both markets’ returns reveals fat tails. Therefore, the GARCH and CARR model are, at first glance, capable of fitting the S&P 500 and NIKKEI 225 market trading data.
Table 2 expresses the parameter estimation results for the DCC-GARCH (1,1) and DCC-CARR (1,1) models with the futures and spot indices, respectively. According to Engle [34], this study uses the quasi-maximum li- kelihood estimation to reduce the problem faced in volatility estimation of over heteroskedasticity. The charac- teristic of return-based and range-based volatility is shown in Panel A of Table 2. Here, the range-based volatil- ity model is more sensitivity than return-based case in capturing volatility transitory shocks. In addition, this study uses the standardized residuals generated from different market data to estimate the parameters of the dy- namic conditional correlation structure. Panel B of Table 2 presents clearly dissimilar dynamic correlation processes.
Billio and Caporin [18] believe that using two regimes to configure the model will limit any problems of convergence. For this reason, this study focuses on the estimation of the range-based MS-DCC model with two different regimes. The estimated results for the two-state range- and return-based MS-DCC model are reported
in Table 3. According to the model specification, the larger coefficient of 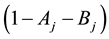
high-correlation regime, and the smaller coefficient of 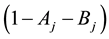
The estimated transition probability of remaining in the low-correlation state 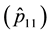
dices; however, the estimated transition probability of remaining in the high-correlation state 
from low to high correlation 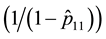
225, but the expected transition period from high to low correlation 
for the S&P 500 and 0.03 years for the NIKKEI 2256. This finding indicates that the expected transition period from high to low correlation is shorter than that of the reverse and that the correlation is relatively stable in the long term, although shocks may cause the correlation to oscillate violently and move from a low to high state. This study also calculates the steady-state probabilities of the Markov process as a benchmark. The estimated result of the range-based MS-DCC model indicates that the steady-state probability that the correlation of the S&P 500 will move to a low (high) state in the next period is 0.810 (0.190) and that the probability that the cor- relation of the NIKKEI 225 will move to a low (high) state in the next period is 0.998 (0.002). In brief, the probability of the expected correlation for either stock index moving to a low state is over 80%. With regard to the dynamic correlation process, the high-correlation state has a larger value of 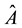
Figure 1 further shows the smoothed probability of the low-correlation state estimated by the range-based Markov-switching DCC model for the S&P 500 and NIKKEI 225 indices. The patterns differ substantially be- tween the two stock indices. This difference may be attributed to the corresponding estimated transition proba- bility figures. In addition, this finding is also in line with the inference of the expected transition period, which is shown in Table 3. Figure 1 shows that the estimated time-varying correlation has higher probability of remain- ing in the low-correlation regime for the NIKKEI 225 spot and futures indices than for the S&P 500. The find-
Table 1. Descriptive statistics for the daily returns and ranges of spot and futures of S&P 500 and of NIKKEI 225 (2000.1.3-2011.6.29).
Notes: The Bera-Jarque is the statistic for normality testing.
Table 2. The estimation of range- and return-based dynamic conditional correlation model of daily spot and futures of S&P 500 and of NIKKEI 225 (2000.1.3-2011.6.29).
Notes: The number in parentheses is robust standard error proposed by Bollerslev and Wooldridge [33] .
ing that the high-correlation regime follows major financial events, especially in the case of the S&P 500, makes intuitive sense7.
Table 3. The estimation of range- and return-based markov switching dynamic conditional correlation model for daily spot and futures of S&P 500 and NIKKEI 225 (2000.1.3-2011.6.29).
Notes: The number in parentheses is robust standard error proposed by Bollerslev and Wooldridge [33]. The probability of staying in the low correlation state is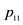
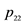
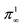
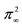

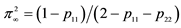
Figure 1. The smoothed probability of low correlation regime for S&P 500 and NIKKEI 225 (2000.1.3 - 2011.6.29). This figure plots the smoothed probability estimated by range-based Markov-switching dynamic conditional correlation model.
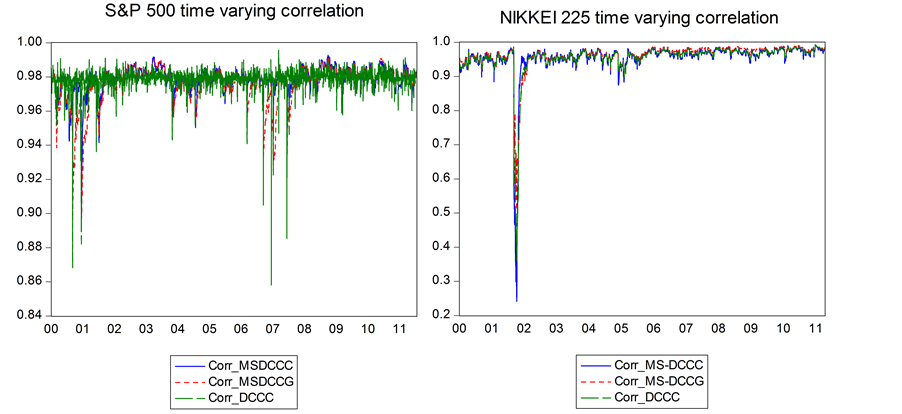
Figure 2 displays the estimated time-varying correlations of the return-based MS-DCC, range-based DCC and MS-DCC models for the S&P 500 and NIKKEI 225. For both stock indices, the fluctuating range of time-varying correlation estimated from the range data is wider than that estimated from return data. The largest range of fluctuation is estimated by the range-based DCC model for the S&P 500, but the range-based MS-DCC model estimates the largest range for the NIKKEI 2258. The correlations estimated by the range-based MS-DCC are less volatile than those estimated by the range-based DCC for the S&P 500, but the estimated results are the opposite for the NIKKEI 225. This finding indicates that the use of range data could lead to correlation estimates with a wider range compared to those produced using return data. Furthermore, considering a regime-switching method for the range-based DCC model could make the correlation estimates more flexible, as the regime- switching method can capture reactions to variation with greater precision.
Table 4 reports the in-sample and out-of-sample forecasting performance summary for various measurements of hedging ratios. The degree of risk aversion is assumed to be k = 4 for the expected daily utility function in Equation (18)9. In the case of given parameters for the VaR estimate, the initial value and the quantile of normal distribution are assumed to be 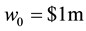
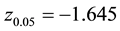
8The range of fluctuation in the time-varying correlation for S&P 500 is (0.8581, 0.9957) for the range-based DCC, (0.8964, 0.9909) for the return-based MS-DCC, and (0.8947, 0.9932) for the range-based MS-DCC. However, the range of fluctuation in the time-varying correlation for NIKKEI 225 is (0.3597, 0.9915) for the range-based DCC, (0.5083, 0.9910) for the return-based MS-DCC, and (0.2413, 0.9932) for the range-based MS-DCC.
9This setting of the degree of risk aversion is in line with Alizadeh and Nomikos [25] and Alizadeh et al. [35] .
10Engel [36] and Marsh [37] clarify that parameter instability may lead to differences between in-sample and out-of-sample performance.
11The hedge portfolio is calculated as 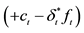
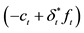
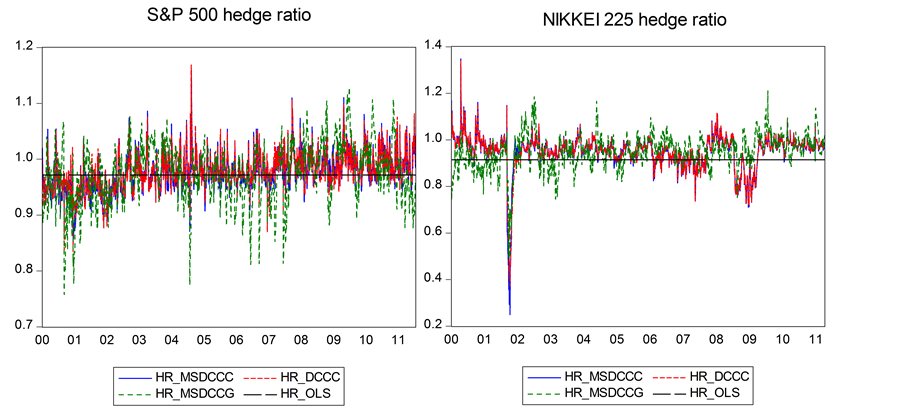
Figure 3 shows the optimal hedge ratios estimated by the constant OLS, return-based MS-DCC, range-based DCC and MS-DCC models for the S&P 500 and NIKKEI 225. The hedge ratios of the range-based MS-DCC model are more volatile than those of competing models in the case of the NIKKEI 225; however, different outcomes are found in the case of the S&P 500. This finding is consistent with the results shown in Figure 2.
Table 5 presents the out-of-sample performance of various hedging ratios in terms of downside risk for the short and long hedgers. In Panel A, all of the effectiveness criteria for the short hedger indicate that the range- based MS-DCC model is the most effective hedging strategy for the S&P 500. However, the naïve hedging strategy shows the best performance for the NIKKEI 225. This result from Panel A of Table 5 is almost identic- al to that from Panel B of Table 4, as both of these calculations are based on short hedgers. Comparing Panel A of Table 5 with Panel B of Table 4, the VaR figures calculated from the semi-standard deviation for each hedg- ing strategy are larger than the corresponding half-VaR figures estimated using the standard deviation.
Figure 2. The estimated time varying correlations for S&P 500 and NIKKEI 225 (2000.1.3-2011.6.29). This figure plots three estimated time varying correlations including range-based DCC (Corr_DCCC), MS-DCC (Corr_MSDCCC) and return-based MS-DCC (Corr_MSDCCG) models.
Figure 3. The constant OLS, return-based MS-DCC, range-based DCC and MS-DCC hedge ratios for S&P 500 and NIKKEI 225 (2000.1.3-2011.6.29). This figure plots four hedge ratios estimated from constant OLS (HR_OLS), return-based MS-DCC (HR_MSDCCG), range-based DCC (HR_DCCC) and MS-DCC (HR_ MSDCCC) models.
This finding indicates that using semi-variance to substitute for the variance is meaningful, as the hedge portfo- lio has a significantly asymmetric return distribution. In terms of long hedgers, the empirical results mostly in- dicate the outperformance of the range-based MS-DCC model over competing models for both stock indices, as shown in Panel B of Table 5. Considering the trading position and downside risk, the hedging effectiveness of the range-based MS-DCC model remains superior to competing models for the S&P 500. Although the results of the short hedger indicate the outperformance of the naïve hedging strategy for NIKKEI 225, the range-based MS-DCC model is found show superior hedging performance for the long hedger. In addition, the estimated VaR figures indicate that the use of the range-based MS-DCC model in a hedging strategy can reduce the losses by between 0.979 million to 1.474 million for either stock index. We can infer that the in-sample and out- of-sample performance verifies that the range-based MS-DCC model can increase not only the variance (semi- variance) improvement term but also the economic benefit measures.
Table 4. Hedging effectiveness of range-based Markov switching dynamic conditional correlation model against the alter- native hedge ratio models for daily spot and futures of S&P 500 and NIKKEI 225 (2000.1.3-2011.6.29).
Notes: VI is the variance improvement of unhedged model against the other competing models, and it is calculated as: [Var(unhedged)- Var(modeli)]/Var(unhedged). Daily utility is calculated by the mean-variance utility function and the coefficient of risk aversion is 4. VaR(5%) is the value at risk.
Table 5. Effectiveness short/long hedger of range-based Markov switching dynamic conditional correlation model against the alternative hedge ratio models for daily spot and futures of S&P 500 and NIKKEI 225 (2000.1.3-2011.6.29).
Notes: Semi-variance denotes the variability of returns below the mean return. Semi-VI is the semi-variance improvement of unhedged model against the other competing models, and it is calculated as: [Semi-Var(unhedged)-Semi-Var(modeli)]/Semi-Var(unhedged). Semi-daily utility is calculated by the mean-semi-variance utility function and the coefficient of risk aversion is 4. VaR(5%) is the value at risk calculated by the semi-standard devia- tion.
6. Conclusion
In this study, a new range-based Markov-switching dynamic conditional correlation model is proposed to ad- dress minimum variance hedging for futures. Under this specification, the range-based MS-DCC model ad- dresses flaws of the linear functional forms of the conventional conditional covariance estimation method. For the empirical study, spot and futures data of the value-weighted S&P 500 index and the equal-weighted NIKKEI 225 index are collected to estimate the range-based MS-DCC model. The estimated results show that the dy- namic correlation process is derived by both the low- and high-correlation states by means of an estimated en- dogenous transition probability for both stock indices. This finding indicates that incorporating a regime- switching mechanism into the dynamic correlation process can show more realistic variation in correlation pat- terns. In addition, the calculated transition period shows that the frequency of switching from high to low corre- lation is lower than that of the reverse. The graph of smoothed probability clearly shows that important financial events lead correlation to move to a high regime, especially in the case of the S&P 500. We believe that this ad- vantage can lead to outperformance in minimum-variance hedging. This study introduces several different cor- relation models to calculate the minimum-variance hedging ratio and then compares their hedging effectiveness in terms of three criteria. Overall, the in-sample and out-of-sample performance indicates that the use of the range-based MS-DCC model for hedging leads to superior variance (semi-variance) improvement and greater economic benefits.
References
- Engle, R. (2002) Dynamic Conditional Correlation―A Simple Class of Multivariate GARCH Models. Journal of Business and Economic Statistics, 20, 339-350. http://dx.doi.org/10.1198/073500102288618487
- Bollerslev, T., Engle, R. and Wooldridge, J.M. (1988) A Capital Asset Pricing Model with Time Varying Covariances. Journal of Political Economy, 96, 116-131. http://dx.doi.org/10.1086/261527
- Engle, R. and Kroner, K. (1995) Multivariate Simultaneous GARCH. Econometric Theory, 11, 122-150. http://dx.doi.org/10.1017/S0266466600009063
- Bollerslev, T. (1990) Modeling the Coherence in Short-Run Nominal Exchange Rates: A Multivariate Generalized ARCH Model. Review of Economics and Statistics, 72, 498-505. http://dx.doi.org/10.2307/2109358
- Parkinson, M. (1980) The Extreme Value Method for Estimating the Variance of the Rate of Return. Journal of Busi- ness, 53, 61-65. http://dx.doi.org/10.1086/296071
- Rogers, C. and Satchell, S. (1991) Estimating Variance from High, Low and Closing Prices. Annals of Applied Proba- bility, 1, 504-512. http://dx.doi.org/10.1214/aoap/1177005835
- Yang, D. and Zhang, Q. (2000) Drift-Independent Volatility Estimation Based on High, Low, Open, and Close Prices. Journal of Business, 73, 477-491. http://dx.doi.org/10.1086/209650
- Alizadeh, S., Brandt, M. and Diebold, F. (2002) Range-Based Estimation of Stochastic Volatility Models. Journal of Finance, 57, 1047-1091. http://dx.doi.org/10.1111/1540-6261.00454
- Brandt, M. and Jones, C. (2006) Volatility Forecasting with Range-Based EGARCH Models. Journal of Business and Economic Statistics, 24, 470-486. http://dx.doi.org/10.1198/073500106000000206
- Chou, R.Y. (2005) Forecasting Financial Volatilities with Extreme Values: The Conditional Autoregressive Range (CARR) Model. Journal of Money Credit and Banking, 37, 561-582. http://dx.doi.org/10.1353/mcb.2005.0027
- Chou, R.Y. (2006) Modeling the Asymmetry of Stock Movements Using Price Ranges. Advances in Econometrics, 20, 231-258. http://dx.doi.org/10.1016/S0731-9053(05)20009-9
- Chou, R.Y., Wu, C.C. and Liu, N. (2009) Forecasting Time-Varying Covariance with a Range-Based Dynamic Condi- tional Correlation Model. Review of Quantitative Finance and Accounting, 33, 327-345. http://dx.doi.org/10.1007/s11156-009-0113-3
- Cai, Y., Chou, R.Y. and Li, D. (2009) Explaining International Stock Correlations with CPI Fluctuations and Market Volatility. Journal of Banking and Finance, 33, 2026-2035. http://dx.doi.org/10.1016/j.jbankfin.2009.05.013
- Danielsson, J. (2011) Financial Risk Forecasting: The Theory and Practice of Forecasting Market Risk with Implementation in R and Matlab. John Wiley, Hoboken.
- Hamilton, J.D. (1989) A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle. Econometrica, 57, 357-384. http://dx.doi.org/10.2307/1912559
- Hamilton, J.D. (1990) Analysis of Time Series Subject to Changes in Regime. Journal of Econometrics, 45, 39-70. http://dx.doi.org/10.1016/0304-4076(90)90093-9
- Pelletier, D. (2006) Regime Switching for Dynamic Correlations. Journal of Econometrics, 131, 445-473. http://dx.doi.org/10.1016/j.jeconom.2005.01.013
- Billio, M. and Caporin, M. (2005) Multivariate Markov Switching Dynamic Conditional Correlation GARCH Repre- sentations for Contagion Analysis. Statistical Method and Applications, 14, 145-161. http://dx.doi.org/10.1007/s10260-005-0108-8
- Chen, S., Lee, C. and Shreatha, K. (2003) Futures Hedge Ratios: A Review. The Quarterly Review of Economics and Finance, 43, 433-465. http://dx.doi.org/10.1016/S1062-9769(02)00191-6
- Lien, D. and Tse, Y. (2002) Some Recent Developments in Futures Hedging. Journal of Economic Surveys, 16, 357- 396. http://dx.doi.org/10.1111/1467-6419.00172
- Baillie, R.T. and Myers, R. (1991) Bivariate GARCH Estimation of the Optimal Commodity Futures Hedge. Journal of Applied Econometrics, 6, 109-124. http://dx.doi.org/10.1002/jae.3950060202
- Kroner, K.F. and Sultan, J. (1993) Time-Varying Distributions and Dynamic Hedging with Foreign Currency Futures. Journal of Finance and Quantitative Analysis, 28, 535-551. http://dx.doi.org/10.2307/2331164
- Tong, W.H.S. (1996) An Examination of Dynamic Hedging. Journal of International Money and Finance, 15, 19-35. http://dx.doi.org/10.1016/0261-5606(95)00040-2
- Choudhry, T. (2003) Short Run Deviations and Optimal Hedge Ratio: Evidence from Stock Futures. Journal of Multi- national Financial Management, 13, 171-192. http://dx.doi.org/10.1016/S1042-444X(02)00042-7
- Alizadeh, A. and Nomikos, N. (2004) A Markov Regime Switching Approach for Hedging Stock Indexes. Journal of Futures Markets, 24, 649-674. http://dx.doi.org/10.1002/fut.10130
- Lien, D., Tse, Y. and Tsui, A. (2002) Evaluating the Hedging Performance of the Constant-Correlation GARCH Model. Applied Financial Economics, 12, 791-798. http://dx.doi.org/10.1080/09603100110046045
- Copeland, L. and Zhu, Y. (2006) Hedging Effectiveness in the Index Futures Market. Cardiff Economics Working Papers from Cardiff University, Cardiff Business School, Economics Section, Colum Drive, Cardiff.
- Alexander, C. and Barbosa, A. (2007) Effectiveness of Minimum Variance Hedging. Journal of Portfolio Management, 33, 46-59. http://dx.doi.org/10.3905/jpm.2007.674793
- Lien, D. (2005) The Use and Abuse of the Hedging Effectiveness Measure. International Review of Financial Analysis, 14, 277-282. http://dx.doi.org/10.1016/j.irfa.2004.11.001
- Lien, D. (2009) A Note on the Hedging Effectiveness of GARCH Models. International Review of Economics and Finance, 18, 110-112. http://dx.doi.org/10.1016/j.iref.2007.07.004
- Lien, D. (2010) A Note on the Relationship between the Variability of the Hedge Ratio and Hedging Performance. Journal of Futures Markets, 30, 1100-1104. http://dx.doi.org/10.1002/fut.20455
- Ederington, L.H. (1979) The Hedging Performance of the New Futures Markets. Journal of Finance, 34, 157-170. http://dx.doi.org/10.1111/j.1540-6261.1979.tb02077.x
- Bollerslev, T. and Wooldridge, J.M. (1992) Quasi Maximum Likelihood Estimation and Inference in Dynamic Models with Time Varying Covariances. Econometric Reviews, 11, 143-172. http://dx.doi.org/10.1080/07474939208800229
- Engle, R. (2001) GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. Journal of Economic Perspectives, 15, 157-168. http://dx.doi.org/10.1257/jep.15.4.157
- Alizadeh, A., Nomikos, N. and Pouliasis, P.K. (2008) A Markov Regime Switching Approach for Hedging Energy Commodities. Journal of Banking and Finance, 32, 1970-1983. http://dx.doi.org/10.1016/j.jbankfin.2007.12.020
- Engel, C. (1994) Can the Markov Switching Model Forecast Exchange Rates? Journal of International Economics, 36, 151-165. http://dx.doi.org/10.1016/0022-1996(94)90062-0
- Marsh, I.W. (2000) High Frequency Markov Switching Models in the Foreign Exchange Market. Journal of Forecasting, 19, 123-134. http://dx.doi.org/10.1002/(SICI)1099-131X(200003)19:2<123::AID-FOR750>3.0.CO;2-C
- Cotter, J. and Hanly, J. (2006) Reevaluating Hedging Performance. Journal of Futures Markets, 26, 677-702. http://dx.doi.org/10.1002/fut.20212
NOTES
*Corresponding author.
1The generalization of the univariate volatility models to the multivariate case is the VECH model, introduced by Bollerslev et al. [2] . How- ever, the VECH model has some disadvantages, including problems determining a positive definite and the possibility of including too many parameters. In response, Engle and Kroner [3] propose the BEKK model to guarantee a positive definite constraint. However, the BEKK model still has the problem of facing too many parameter estimations for higher dimensional systems. Although the VECH and BEKK mod- el have some drawbacks, they are more flexible than the constant correlation model in allowing time-varying covariance (Bollerslev, [4] ).
2Also see Parkinson [5] , Rogers and Satchell [6] , Yang and Zhang [7] , Alizadeh, et al. [8] , Brandt and Jones [9] , Chou [10] [11] , Chou, et al. [12] and Cai, et al. [13] .
3Also see Danielsson [14] .
4See also Baillie and Myers [21] , Kroner and Sultan [22] , Tong [23] , Choudhry [24] and Alizadeh and Nomikos [25] .
5See also Lien, et al. [26] , Copeland and Zhu [27] and Alexander and Barbosa [28] .
6The calculated transition period is deliberately displayed as an annualized figure for ease of comparison.
7These financial events include the 2000 technology bubble, the September 11 terrorist attacks, the 2002 stock market crash, the 2007 sub- prime housing crisis and the 2009 credit crisis.