Journal of Mathematical Finance
Vol.4 No.2(2014), Article ID:43336,10 pages DOI:10.4236/jmf.2014.42011
Pricing of Margrabe Options for Large Investors with Application to Asset-Liability Management in Life Insurance
Centre of Mathematics for Applications, University of Oslo, Oslo, Norway
Email: erikb@math.uio.no, proske@math.uio.no, mark.rubtsov@gmail.com
Received September 30, 2013; revised November 25, 2013; accepted December 19, 2013
ABSTRACT
We study a problem related to asset-liability management in life insurance. As shown by Wüthrich, Bühlmann and Furrer in [1], an insurance company can guarantee solvency by purchasing a Margrabe option enabling it to exchange its asset portfolio for a valuation portfolio. The latter can be viewed as a replicating portfolio for the insurance liabilities in terms of financial instruments. Our objective in this paper is to investigate numerically a valuation technique for such an option in a situation when the insurance company is a “large” investor, implying that its trading decisions can affect asset prices. We view this situation through the framework employed in the Cvitanić and Ma’s 1996 paper [2] and use the method of finite differences to solve the resulting non-linear PDE. Our results show reliability of this numerical method. Also we find, similarly to other authors, that the option price for the large investor is higher than that for a Black-Scholes trader. This makes it particularly compelling for a large insurance company to purchase a Margrabe option at the Black-Scholes price.
Keywords:Margrabe Option; Large Investor; Finite Differences Method
1. Introduction
Usual continuous-time financial models assume that investor’s behaviour does not affect stock prices. This idea is known under the name “small investor hypothesis”, implying that each investor is assumed to be unable to move market prices by his trading decisions and acts as a price taker. In contrast to that hypothesis, many authors investigated a setting in which market prices depend on the size of the transaction. This research direction can be classified into two broad categories. The first one deals with liquidity risk and investigates its impact on asset prices and hedging strategies. In particular, Cetin, Jarrow and Protter [3] and Cetin, Soner, and Touzi [4] assume that market prices result from interaction of small price taking investors with an exogenously given asset supply curve. The latter determines the price for a given transaction size. This research category also includes Cetin and Rogers [5], Rogers and Singh [6], as well as Soner and Gökay [7], among others.
The second type of literature in this research direction focuses on feedback effects of hedging strategies on underlying asset prices. It is assumed that a large investor can—directly or indirectly—affect market prices. In particular, Platen and Schweizer [8] show that large investor’s hedging decisions can lead to increased volatility of the underlying asset. Frey and Stremme [9] also present a model in which the existence of a large trader results in higher market volatility. These authors, as well as Jarrow [10], Frey [11], and Papanicolau and Sicar [12] model stock prices as being directly dependent on large investor’s stock holdings through a certain reaction function. Bank and Baum [13] use a similar reaction function setting to the one employed by Frey and Stremme [9] to specify the dynamics of the asset price as a semi-martingale parametrized by the large investor’s position in the stock. In contrast to their approach, Cvitanić and Ma [2], as well as Cuoco and Cvitanić [14], assume that parameters in the diffusion driving the evolution of the stock price, rather than the price itself, depend on large investor’s trading decisions. DeMarzo and Urosevic [15] develop a general equilibrium model that justifies the models used by Cvitanić and Ma [2] and Cuoco and Cvitanić [14].
The present paper belongs to the second group. We adopt the framework used by Cvitanić and Ma [2] to study the problem faced by an insurance company that wants to achieve solvency. This can be done by means of a Margrabe option that gives the company the right to exchange its asset portfolio for a valuation portfolio. The latter is a replicating portfolio for the insurance company’s liabilities. One can obtain the price of a Margrabe option within the Black-Scholes setting by representing it as a standard European Put option written on a certain artificial asset. However, if the company is a large investor whose hedging strategies can have a feedback effect on the price of the underlying asset, one needs to use different pricing methodology. In this paper it is assumed that market volatility depends on the value of the replicating portfolio held by the large investor and the amount of money he invests in the asset. Our objective is to study the hedging problem faced by the large investor. Namely, we intend to find the price of and the hedging strategy for the Margrabe option in a situation where the insurance company is no longer a price taker. In mathematical terms, the problem translates into a forwardbackward stochastic differential equation. The solution of its backward part gives us the quantities we are looking for.
The paper is organised as follows. Section two presents the model, explains the derivation of the associated FBSDE and PDE and ends with an explanation of a numerical scheme that will be used to obtain the solution. Section three discusses the application at hand. It gives a brief overview of the relevant material in Wüthrich, Bühlmann, and Furrer [1] and puts it in the context of the large investor problem. Section four gives details of numerical simulations and presents our findings. Section five concludes.
2. Mathematical Model
We study the hedging problem for a large investor on a finite time horizon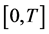 , given the initial stock price
, given the initial stock price 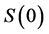 and the terminal wealth
and the terminal wealth  referring to the pay-off of the option to be hedged. The objective of the hedger is to find a portfolio process and the minimal initial wealth
referring to the pay-off of the option to be hedged. The objective of the hedger is to find a portfolio process and the minimal initial wealth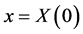 , such that at the option’s expiration date
, such that at the option’s expiration date .
.
We assume that there are two investment possibilities on the market:
• Bond with the following dynamics:
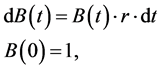 (1.1)
(1.1)
where  is a riskless interest rate.
is a riskless interest rate.
• Stock that follows the dynamics:
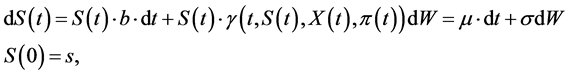 (1.2)
(1.2)
where 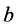 is a constant drift,
is a constant drift, 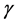 is an appropriate volatility function,
is an appropriate volatility function, 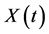 is the the value of the replicating portfolio held by large investor and
is the the value of the replicating portfolio held by large investor and 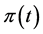 is the amount of money he invests in the stock. The main thing to be noticed here is that stock’s volatility is assumed to depend on large investor’s strategies.
is the amount of money he invests in the stock. The main thing to be noticed here is that stock’s volatility is assumed to depend on large investor’s strategies. 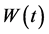 is a standard Brownian motion defined on a complete probability space
is a standard Brownian motion defined on a complete probability space  with filtration generated by
with filtration generated by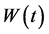 .
.
The investor begins with a certain endowment 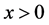 and allocates his wealth in the stock and the bond according to a certain strategy. The portfolio process
and allocates his wealth in the stock and the bond according to a certain strategy. The portfolio process 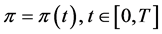 is assumed to be a real-valued, progressively measurable, square-integrable stochastic process.
is assumed to be a real-valued, progressively measurable, square-integrable stochastic process.
At each point of time the value of the replicating portfolio equals:
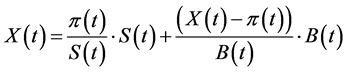 (1.3)
(1.3)
and has the following dynamics:
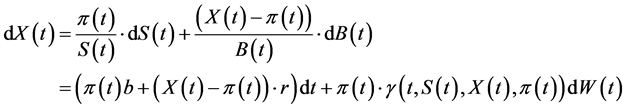 (1.4)
(1.4)
Following [2], we introduce the following assumptions.
• The drift and volatility functions in the stock price dynamics,  , and
, and , are twice continuously differentiable. The functions
, are twice continuously differentiable. The functions 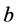 and
and 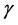 together with their first order partial derivatives are bounded uniformly in
together with their first order partial derivatives are bounded uniformly in . Further, it is assumed that partial derivatives of
. Further, it is assumed that partial derivatives of 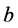 and
and 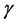 in
in 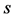 satisfy
satisfy
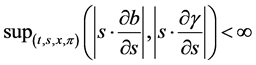 (1.5)
(1.5)
• There exists a positive constant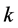 , such that
, such that  for all
for all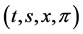 .
.
According to Lemma 2.3 in [2] these assumptions guarantee that the stock price remains almost surely positive.
• Also, we assume that option’s pay-off function 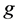 is non-negative,
is non-negative,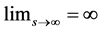 . Moreover,
. Moreover, 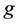 has bounded, continuous partial derivatives up to third order and there exist constants
has bounded, continuous partial derivatives up to third order and there exist constants  and
and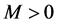 , such that
, such that
 (1.6)
(1.6)
and
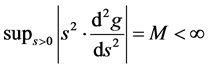 (1.7)
(1.7)
In order to satisfy these assumptions we use the following smoothed pay-off function (suggested in [11]):
 (1.8)
(1.8)
where 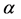 is a smoothing parameter.
is a smoothing parameter.
• Finally, we assume that partial derivatives of 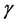 in
in 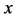 and
and  satisfy the following condition.
satisfy the following condition.
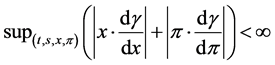 (1.9)
(1.9)
These assumptions are satisfied by the constant drift coefficient  in SDE (1.2) and the following volatility function (suggested in [2])
in SDE (1.2) and the following volatility function (suggested in [2])
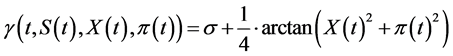 (1.10)
(1.10)
Definition 1 ([2]) For any given initial wealth  the portfolio process
the portfolio process  is called admissible (with respect to
is called admissible (with respect to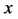 ) if for any
) if for any 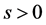 the corresponding price process
the corresponding price process 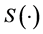 and wealth process
and wealth process 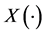 satisfy
satisfy 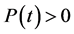 and
and . For each initial wealth
. For each initial wealth , we denote the set of admissible portfolio strategies by
, we denote the set of admissible portfolio strategies by .
.
We are now going to formulate the hedging problem in terms of a forward-backward stochastic differential equation. Consider a FBSDE given by the stock price SDE—the forward part—and the BSDE describing the evolution of the portfolio wealth—the backward part.
 (1.11)
(1.11)
Definition 2 ([2]) A triple 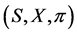 is called an adapted solution of FBSDE (1.11) if
is called an adapted solution of FBSDE (1.11) if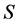 ,
, 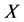 and
and  are
are 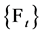 -adapted, square-integrable stochastic processes.
-adapted, square-integrable stochastic processes.
The assumptions in the previous section guarantee that the FBSDE (1.11) has a unique adapted solution, as shown in [2].
We now intend to obtain a partial differential equation characterising the FBSDE (1.11). Denote  and
and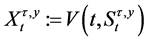 . Then by the Itô’s formula
. Then by the Itô’s formula
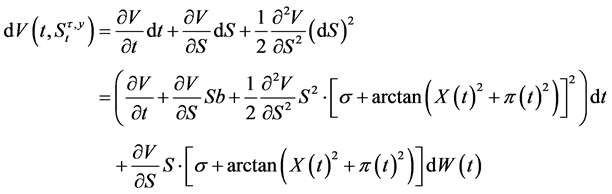 (1.12)
(1.12)
At the same time, as can be seen from SDE (1.4)
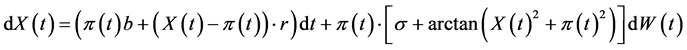 (1.13)
(1.13)
Matching the 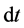 and
and  terms we find the following:
terms we find the following:
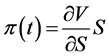 (1.14)
(1.14)
 (1.15)
(1.15)
Condition (1.14) gives us the hedging strategy right away. Combining it with Equation (1.15) produces the following PDE:
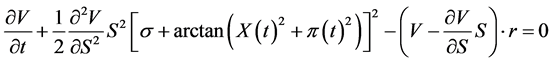 (1.16)
(1.16)
This is a quasi-liner parabolic partial differential equation that needs to be solved in order to obtain function
 , which represents the option price, as well as its first derivative
, which represents the option price, as well as its first derivative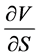 , which is needed to compute the hedging strategy.
, which is needed to compute the hedging strategy.
Obtaining an analytical solution for PDE (1.16) is rather formidable. Instead, it can be solved by means of the Finite Differences method. In particular, we are going to employ the Predictor-Corrector method, which is successfully used to solve non-linear PDEs and described in [16].
The idea of the method is the following. First, we split the time interval  and the space interval
and the space interval 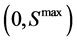 into
into  and
and  subintervals, correspondingly, and denote by
subintervals, correspondingly, and denote by , where
, where
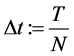 and
and . Then, we write down an explicit finite difference scheme for PDE (1.16). We use the backward finite difference in time and the central finite difference in space in order to approximate the first order partial derivatives of function
. Then, we write down an explicit finite difference scheme for PDE (1.16). We use the backward finite difference in time and the central finite difference in space in order to approximate the first order partial derivatives of function 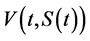 with respect to
with respect to 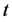 and
and 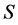 respectively.
respectively.
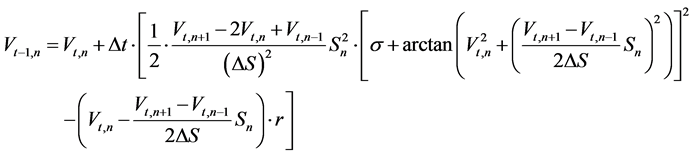 (1.17)
(1.17)
The value 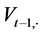 obtained this way is a preliminary estimate that is to be “corrected” through the use of the implicit scheme, which looks as follows:
obtained this way is a preliminary estimate that is to be “corrected” through the use of the implicit scheme, which looks as follows:
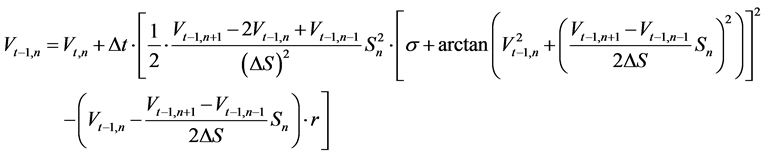 (1.18)
(1.18)
In the traditional case, the use of the implicit scheme (1.18) would involve a solution of a non-liner system of equations, which would require numerical methods for itself. Instead, the predictor-corrector method suggests using the preliminary estimate of 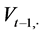 obtained in (1.17) to substitute for the corresponding values on the right hand side of (1.18). Thus, we obtain a cyclical algorithm for consecutive computation of
obtained in (1.17) to substitute for the corresponding values on the right hand side of (1.18). Thus, we obtain a cyclical algorithm for consecutive computation of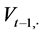 :
:
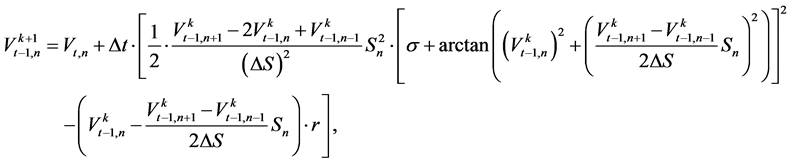 (1.19)
(1.19)
where the initial  needed to initiate the cycle is obtained from the explicit scheme (1.17). The algorithm is exited after a predefined number of iterations, or when a certain measure of distance between the consecutive solutions falls below a pre-specified value.
needed to initiate the cycle is obtained from the explicit scheme (1.17). The algorithm is exited after a predefined number of iterations, or when a certain measure of distance between the consecutive solutions falls below a pre-specified value.
The initial condition in this numerical scheme comes from the option’s pay-off function, while boundary conditions are obtained by using the put-call parity.
3. Application: Asset-Liability Management in Life Insurance
This section relies on material in [1]. The central problem in insurance business is solvency. In simple words, a company is called solvent if it is able to meet all its financial obligations. FormallyDefinition 3 ([1]) A company is solvent at time  if
if
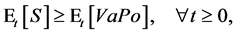 (1.20)
(1.20)
where 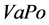 is a valuation portfolio, which can be viewed as a replicating portfolio for the insurance liabilities in terms of financial instruments;
is a valuation portfolio, which can be viewed as a replicating portfolio for the insurance liabilities in terms of financial instruments; 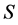 is the existing asset portfolio of the insurance company;
is the existing asset portfolio of the insurance company;  is the accounting principle used to value assets and liabilities. A usual choice is the economic accounting principle, which corresponds to the valuation at current market prices.
is the accounting principle used to value assets and liabilities. A usual choice is the economic accounting principle, which corresponds to the valuation at current market prices.
The goal of asset-liability management is to maximize returns on company’s assets under the solvency constraint (1.20). An obvious way to guarantee solvency is to invest in the valuation portfolio, i.e. company’s assets consist of 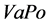 and a certain excess capital
and a certain excess capital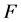 , which must always be non-negative. However, a mismatch between the actual company’s assets and
, which must always be non-negative. However, a mismatch between the actual company’s assets and  is often preferred due to company’s desire to maximize its returns. In this case solvency is guaranteed through the use of a Margrabe option. The latter is the right to exchange one asset for another at a pre-specified time moment. We consider a time period
is often preferred due to company’s desire to maximize its returns. In this case solvency is guaranteed through the use of a Margrabe option. The latter is the right to exchange one asset for another at a pre-specified time moment. We consider a time period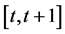 . At
. At 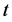 we decompose company’s assets as follows:
we decompose company’s assets as follows:
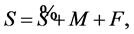 (1.21)
(1.21)
where 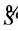 is an asset portfolio satisfying the solvency condition (1.20);
is an asset portfolio satisfying the solvency condition (1.20); 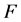 denotes free reserves or excess capital; and
denotes free reserves or excess capital; and  denotes the value of the Margrabe option, giving the holder the right to switch from
denotes the value of the Margrabe option, giving the holder the right to switch from 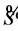 to
to 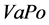 at time
at time , if needed.
, if needed.
The objective now is to price such an option in case company’s trading actions can affect market prices. This situation is not unrealistic, as insurance companies normally manage large asset portfolios and their market trades can also be quite substantial. To formalize the problem we consider two stochastic processes
 (1.22)
(1.22)
and
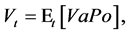 (1.23)
(1.23)
Then by the risk-neutral valuation the price of the Margrabe option is given by
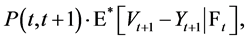 (1.24)
(1.24)
where 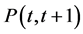 is a zero coupon bond maturing at
is a zero coupon bond maturing at 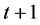 and
and 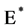 is an expectation under the corresponding risk-neutral measure. Changing the numeraire from
is an expectation under the corresponding risk-neutral measure. Changing the numeraire from 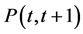 to
to 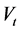 and introducing a new process
and introducing a new process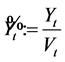 , (1.24) can be rewritten as follows
, (1.24) can be rewritten as follows
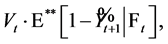 (1.25)
(1.25)
where 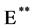 is an expectation with respect to the risk-neutral measure under a new numeraire. Thus, the price of the Margrabe option is equivalent to the price of a European put written on the artificial asset
is an expectation with respect to the risk-neutral measure under a new numeraire. Thus, the price of the Margrabe option is equivalent to the price of a European put written on the artificial asset , having strike
, having strike 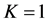 and maturing at
and maturing at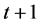 .
.
4. Numerical Simulations
We assume that 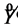 has the following dynamics
has the following dynamics
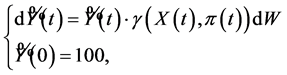 (1.26)
(1.26)
where the volatility function 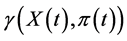 is the same as in (1.10). For the sake of computational stability we assume the initial value of
is the same as in (1.10). For the sake of computational stability we assume the initial value of 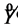 equal 100 instead of 1. The replicating portfolio has the following dynamics
equal 100 instead of 1. The replicating portfolio has the following dynamics
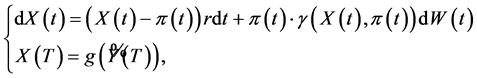 (1.27)
(1.27)
where the terminal condition is given by the smoothed European Put pay-off function with strike equal to 100, as in (1.8)
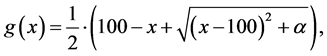 (1.28)
(1.28)
where we take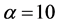 . The PDE to solve is the same as (1.16), with boundary conditions coming from the well known Put-Call parity condition:
. The PDE to solve is the same as (1.16), with boundary conditions coming from the well known Put-Call parity condition:
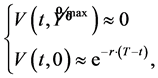 (1.29)
(1.29)
where T is the time of maturity of the option, assumed equal 1. The space interval, represented by possible values of  is assumed to be given by
is assumed to be given by . The time interval spans from 0 to 1. To apply the Finite Difference approach we split the time and space intervals into
. The time interval spans from 0 to 1. To apply the Finite Difference approach we split the time and space intervals into 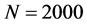 and
and 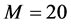 subintervals, correspondingly. Also, we use 3 iteration cycles in the predictor-corrector scheme. The results of the numerical simulations are shown below.
subintervals, correspondingly. Also, we use 3 iteration cycles in the predictor-corrector scheme. The results of the numerical simulations are shown below.
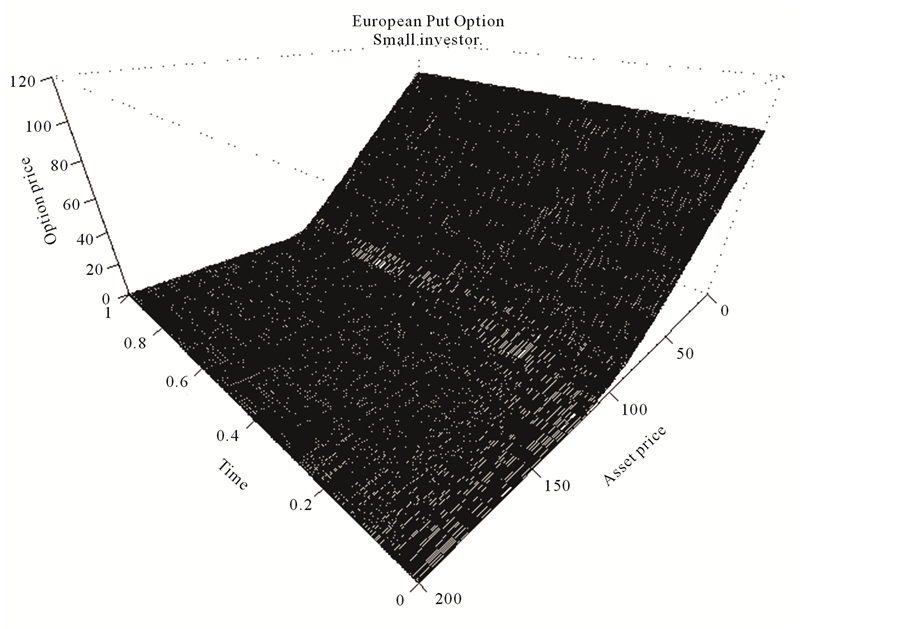
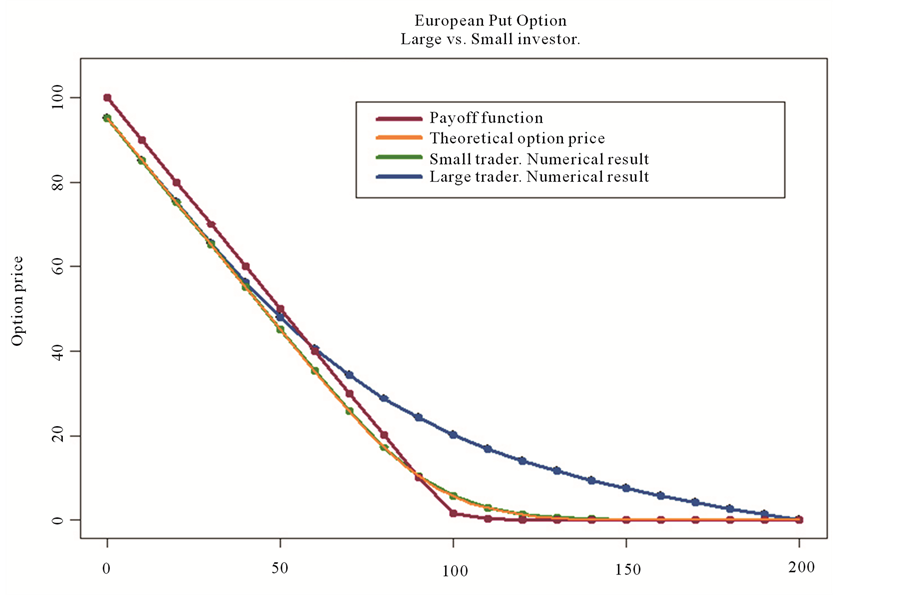
Figure 1(b) shows the dependence of the price of the European Put option for a large investor on time and the price of the underlying asset. The same graph for a small investor is shown in Figure 1(a). A comparison graph in Figure 2(a) shows the difference between option prices for the two investors. It also contains a graph of a theoretical option price computed according to the Black-Scholes formula. As could be expected, the price for the large investor is higher than that for a small investor, highlighting the fact that large investor’s attempts to hedge the option would result in higher volatility of the underlying. It is also seen at the graphs that the derivative  used in computing the hedging strategy, is always positive, implying that the investor must
used in computing the hedging strategy, is always positive, implying that the investor must
 (a)
(a)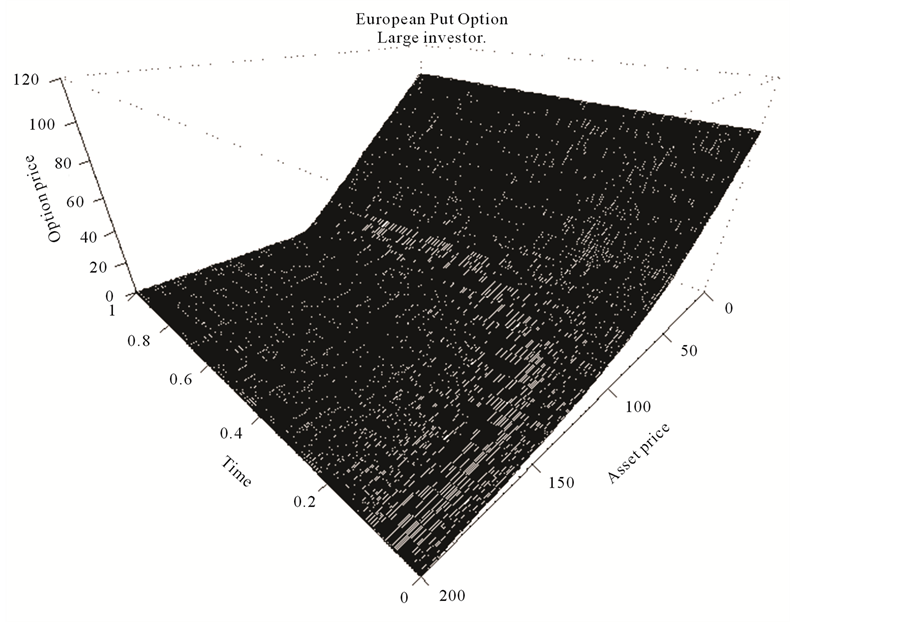 (b)
(b)
Figure 1. The value of the European Put option for the (a) “small”; (b) “large” investor.
 Stock price(a)
Stock price(a) 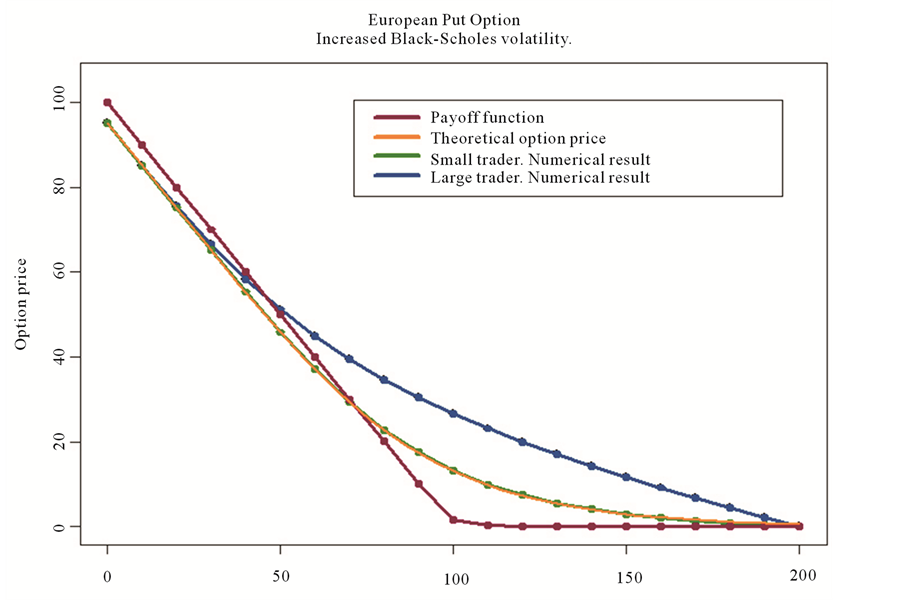 Stock price (b)
Stock price (b)
Figure 2. (a) Price of a European Put option for the “large” vs. “small” investor; (b) Black-Scholes volatility has been increased from 0.2 to 0.4.
always go long in the underlying asset to hedge the option.
The qualitative situation does not change if we alter the underlying Black-Scholes volatility. Figure 2(b) shows comparison results for increased Black-Scholes volatility. We still observe that the large investor’s price is considerably higher than the Black-Scholes one. Our computations confirm that a large investor suffers from adverse conditions when it comes to pricing and hedging options. The necessity to take into account increased volatility of the underlying makes large investor’s hedging strategy more expensive, thus making the option itself more valuable. As for the practical situation under our investigation, one can conclude that buying a Margrabe option from an investor who uses the Black-Scholes formula is a good deal for the large investor, since the replicating alternative would cost him more. Large investor’s direct market involvement in an attempt to construct a replicating portfolio for the Margrabe option would mean a long position in the underlying, thus resulting in higher asset volatility. This situation, in its turn, would compel the large investor to expand his long position even further, leading to higher replicating costs. Our main recommendation to an insurance company in this situation would be to avoid option replication and instead try to buy the Margrabe option from the market.
5. Conclusion
This article investigated the so-called “large” investor problem. The latter refers to the situation when an investor is big enough so that his trade decisions may affect market prices. In particular, we assumed— following Cvitanić and Ma [2]—that the volatility part of the SDE describing the dynamics of the underlying asset depended on the value of the replicating portfolio held by the large investor, as well as his stock holdings. We used this framework to study a problem related to asset-liability management in life insurance. As explained in [1], an insurance company can guarantee its solvency by means of a Margrabe option, which can be seen as a certain European Put option. If the company is a large player on the market, one can use the above framework to compute the corrected option price, the one that takes into account possible feedback effects from company’s hedging strategies onto the dynamics of the underlying. As in Cvitanić and Ma [2], we formulated an FBSDE associated with this problem and derived the PDE, whose solution gives us the corrected option price. One of the objectives of the paper was to investigate the reliability of a numerical scheme—based on the Finite Difference method—that can be used to solve non-linear PDEs. We report the accuracy of the scheme and confirm the result obtained by other authors, namely that the option price for the large investor is normally larger than that for a Black-Scholes trader. This makes it particularly compelling for a large insurance company to purchase a Margrabe option at the Black-Scholes price.
REFERENCES
- M. V. Wüthrich, H. Bühlmann and H. Furrer, “Market-Consistent Actuarial Valuation,” Springer, Berlin, 2008
- J. Cvitanić and J. Ma, “Hedging Options for a Large Investor and Forward-Backward SDE’s,” The Annals of Applied Probability, Vol. 6, No. 2, 1996, pp. 370-398. http://dx.doi.org/10.1214/aoap/1034968136
- U. Cetin, R. Jarrow and P. Protter, “Liquidity Risk and Arbitrage Pricing Theory,” Finance and Stochastics, Vol. 8, No. 3, 2004, pp. 311-341. http://dx.doi.org/10.1007/s00780-004-0123-x
- U. Cetin, H. M. Soner and N. Touzi, “Option Hedging for Small Investors under Liquidity Costs,” Finance and Stochastics, 2007, Forthcoming.
- U. Cetin and L. C. G. Rogers, “Modelling Liquidity Effects in Discrete Time,” Mathematical Finance, Vol. 17, No. 1, 2007, pp. 15-29. http://dx.doi.org/10.1111/j.1467-9965.2007.00292.x
- L. C. G. Rogers and S. Singh, “The Cost of Illiquidity and Its Effects on Hedging,” Preprint, 2007.
- H. M. Soner and S. Gökay, “Cetin-Jarrow-Protter Model of Liquidity in a Binomial Market,” Preprint, 2009.
- E. Platen and M. Schweizer, “On Feedback Effects from Hedging Derivatives,” Mathematical Finance, Vol. 8, No. 1, 1998, pp. 67-84. http://dx.doi.org/10.1111/1467-9965.00045
- R. Frey and A. Stremme, “Market Volatility and Feedback Effects from Dynamic Hedging,” Mathematical Finance, Vol. 7, No. 4, 1997, pp. 351-374. http://dx.doi.org/10.1111/1467-9965.00036
- R. Jarrow, “Derivative Securities Markets, Market Manipulation and Option Pricing Theory,” Journal of Financial and Quantitative Analysis, Vol. 29, No. 2, 1994, pp. 241-261. http://dx.doi.org/10.2307/2331224
- R. Frey, “Perfect Option Hedging for a Large Trader,” Finance and Stochastics, Vol. 2, No. 2, 1998, pp. 115-141. http://dx.doi.org/10.1007/s007800050035
- G. Papanicolaou and R. Sircar, “General Black-Scholes Models Accounting for Increased Market Volatility from Hedging Strategies,” Applied Mathematical Finance, Vol. 5, No. 1, 1998, pp. 45-82. http://dx.doi.org/10.1080/135048698334727
- P. Bank and D. Baum, “Hedging and Portfolio Optimization in Financial Markets with a Large Trader,” Mathematical Finance, Vol. 14, No. 1, 2004, pp. 1-18. http://dx.doi.org/10.1111/j.0960-1627.2004.00179.x
- D. Cuoco and J. Cvitanić, “Optimal Consumption Choice for a Large Investor,” Journal of Economic Dynamics and Control, Vol. 22, No. 3, 1998, pp. 401-436. http://dx.doi.org/10.1016/S0165-1889(97)00065-1
- P. M. DeMarzo and B. Urosevic, “Ownership Dynamics and Asset Pricing with a Large Shareholder,” Journal of Political Economy, Vol. 114, No. 4, 2006, pp. 774-815. http://dx.doi.org/10.1086/506334
- D. J. Duffy, “Finite Difference Methods in Financial Engineering: A Partial Differential Equation Approach,” John Wiley and Sons, Hoboken, 2006. http://dx.doi.org/10.1002/9781118673447

