Journal of Mathematical Finance
Vol.3 No.4(2013), Article ID:38147,11 pages DOI:10.4236/jmf.2013.34046
Optimal Investment and Proportional Reinsurance with Risk Constraint
1School of Insurance, Central University of Finance and Economics, Beijing
2department of Applied Mathematics, The Hong Kong Polytechnic University, Hunghom, China
3Department of Mathematics and Statistics, Curtin University, Perth, Australia
Email: janejz.liu@hotmail.com, macyiu@polyu.edu.hk, R.Loxton@curtin.edu.au, K.L.Teo@curtin.edu.au
Copyright © 2013 Jingzhen Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 6, 2013; revised September 11, 2013; accepted September 29, 2013
Keywords: Proportional Reinsurance; Martingale Transform; Value-at-risk; Stochastic Control; Deterministic Optimal control
ABSTRACT
In this paper, we investigate the problem of maximizing the expected exponential utility for an insurer. In the problem setting, the insurer can invest his/her wealth into the market and he/she can also purchase the proportional reinsurance. To control the risk exposure, we impose a value-at-risk constraint on the portfolio, which results in a constrained stochastic optimal control problem. It is difficult to solve a constrained stochastic optimal control problem by using traditional dynamic programming or Martingale approach. However, for the frequently used exponential utility function, we show that the problem can be simplified significantly using a decomposition approach. The problem is reduced to a deterministic constrained optimal control problem, and then to a finite dimensional optimization problem. To show the effectiveness of the approach proposed, we consider both complete and incomplete markets; the latter arises when the number of risky assets are fewer than the dimension of uncertainty. We also conduct numerical experiments to demonstrate the effect of the risk constraint on the optimal strategy.
1. Introduction
Maximizing the expected utility of wealth is an important objective for an insurer. To achieve this goal, there has been much attention in the literature in security market and/or reinsurance-related products [1-9]. The insurer is tempted to put his/her surplus into the risky investment so as to obtain a higher potential return. However, maximizing profit should not be the only objective. As risky investment could result in a heavy loss, a shrewd insurer should strike a balance between the amount of risky assets and risk-free assets, such that they are kept within bounds. In today’s challenging economic climate, it is clear from the latest report, entitled Financial Reform: A Framework for “Financial Stability” released by The Group of Thirty (G30), that firms must balance risk with caution between the long-term interests of shareholders and returns to shareholders.
One instrument of risk control is reinsurance, which transfers part of the risk exposure to another insurer. In this way, the utility is improved because the reinsurance will help absorb the possible major loss resulting from an insurance claim. However, reinsurance is costly since the insurer has to pay hefty premiums to the reinsurer. This will, in turn, reduce the utility significantly. Thus the optimal choice of reinsurance is also an important issue for the insurer. With a certain risk measure in place, we can control the exposure to risky assets and determine the level of necessary reinsurance.
In risk management, a popular risk measure is valueat-risk (VaR). VaR has emerged as an important risk management tool to estimate the potential loss over a given time period with a given probability. With VaR as the risk constraint, Kostadinova [2] studied the problem of maximizing the expected utility of wealth. In [2], the optimal investment strategy is sought by maximizing the expected wealth of the insurance company with the value-at-risk constraint imposed at the initial date. However, VaR of the portfolio is never reevaluated after the initial date. This is different from the practice adopted by most financial institutions where they use VaR for internal risk control, and VaR is reevaluated frequently. Because the VaR of the portfolio after the initial date, the probability of portfolio losses below the prescribed maximum VaR can become zero after the initial date and yet the trader is still allowed to continue to follow the original trading strategy. This trading strategy is clearly inconsistent with the purpose of imposing the VaR constraint.
In this paper, by allowing both the opportunities of investment and proportional reinsurance, we consider the problem of maximizing the expected exponential utility for the final wealth subject to the VaR constraint. Here, the utility reflects the amount of satisfaction gained by the financial agent from wealth. We impose the VaR as a risk constraint at each instant and emphasize the need for the repeated recalculation of VaR in practice. Moreover, the constraints are calculated abstracting from withininterval trading, based on the available information. In this way, it can be assured that the constraint is consistent with the strategy, see [10-14].
In solving this optimal investment and proportional reinsurance problem, one popular way is to employ the stochastic dynamic programming approach [1,9,15,16]. By using the dynamic programming principle, the problem is reduced to solving a Hamilton-Jacobi-Bellman (HJB) equation, which is a second order linear partial differential equation. A key assumption in this approach is that the value function of the problem is a 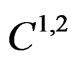 function. This assumption is needed to ensure to obtain the existence of a classical solution to the problem. However, the HJB equation is highly nonlinear. Even its numerical solution is difficult to obtain. This is especially true when the risk constraint is taken into account simultaneously. Moreover, the dynamic programming approach deals with the problems in Markov model setting. For the Martingale approach, it works well in a complete market. Since every Martingale relative to a Brownian filtration can be represented as a stochastic integral with respect to the underlying Brownian motion, the integrand in this representation can lead to the portfolio that we are seeking. However, in an incomplete1 market with a constraint on the strategy or when the number or the risky asset is smaller than the dimension of the driving Brownian, this line of arguments fails.
function. This assumption is needed to ensure to obtain the existence of a classical solution to the problem. However, the HJB equation is highly nonlinear. Even its numerical solution is difficult to obtain. This is especially true when the risk constraint is taken into account simultaneously. Moreover, the dynamic programming approach deals with the problems in Markov model setting. For the Martingale approach, it works well in a complete market. Since every Martingale relative to a Brownian filtration can be represented as a stochastic integral with respect to the underlying Brownian motion, the integrand in this representation can lead to the portfolio that we are seeking. However, in an incomplete1 market with a constraint on the strategy or when the number or the risky asset is smaller than the dimension of the driving Brownian, this line of arguments fails.
In this paper, we study an investment reinsurance problem with a dynamic risk constraint. The approach that we will propose is much easier than the traditional one. It transforms the stochastic optimal control problem into a deterministic optimal control problem. Although the parameters for the assets are assumed to be deterministic functions of time, it appears possible to be extendable to cases, where the parameters are measurable with respect to some filtration defined in the work. Our approach is applicable to cases with or without constraints on the strategy, and whether or not the model setting is Markovian. This provides a different perspective to the investigation of the investment reinsurance problem in actuarial science.
The rest of the paper is structured as follows. In Section 2, we present the investment-reinsurance model with dynamic risk constraint. Here, we consider the wealth maximization problem with the exponential utility function, which plays a prominent role in insurance mathematics and actuarial practice. The exponential utility function is the only utility function under which the principle of “zero utility” gives a fair premium that is independent of the level of reserve of an insurance company (see Gerber [17], page 68). In Section 3, by decomposition, we show that this constrained stochastic optimal control problem can be simplified significantly, reducing to a constrained deterministic optimal control problem and then to a finite-dimensional optimization problem, which can be tackled by classical computation techniques, such as [18-20]. In Section 4, we demonstrate the effectiveness of this method through carrying out numerical experiments for cases of complete and incomplete markets, where the risky assets are fewer than the uncertainty factors (i.e., the dimension of the Brownian motion). We also conduct numerical experiments to investigate the effect of the VaR constraint on the strategy.
2. The Model and the Problem
Suppose that the accumulated claim process 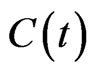 of an insurer can be modeled as:
of an insurer can be modeled as:
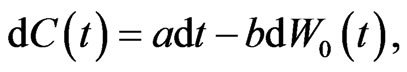 (1)
(1)
where 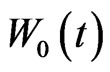 is a standard Brownian motion defined on a complete probability space
is a standard Brownian motion defined on a complete probability space . Let
. Let 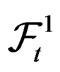 be the filtration generated by
be the filtration generated by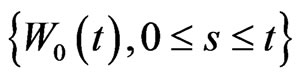 . The surplus process
. The surplus process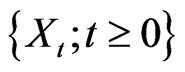 , which represents the liquid assets of the company (also called the risk or the surplus process) is taken as the state variable. With a safety loading
, which represents the liquid assets of the company (also called the risk or the surplus process) is taken as the state variable. With a safety loading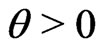 , the continuously paid premium is assumed to be
, the continuously paid premium is assumed to be . In the absence of control, the surplus is governed by
. In the absence of control, the surplus is governed by
 (2)
(2)
where 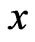 denotes the initial reserve.
denotes the initial reserve.
The proportional reinsurance  is a predictable process with
is a predictable process with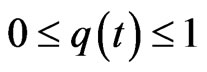 , for
, for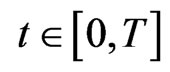 . If the risk exposure of the company is fixed, then the reinsurer pays
. If the risk exposure of the company is fixed, then the reinsurer pays  of each claim while the rest is paid by the insurer. To this end, the cedent diverts part of the premiums to the reinsurer at the rate of
of each claim while the rest is paid by the insurer. To this end, the cedent diverts part of the premiums to the reinsurer at the rate of 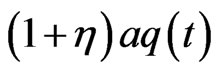 with a proportional loading of
with a proportional loading of .
.
Suppose that the insurer is also allowed to invest its surplus. Assume that the market consists of a risk-free asset and 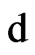 risky assets. The dynamics of the risk-free and the risky assets evolve according to
risky assets. The dynamics of the risk-free and the risky assets evolve according to
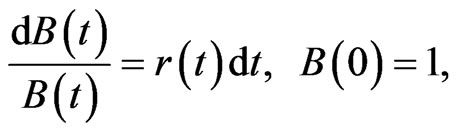 (3)
(3)
and
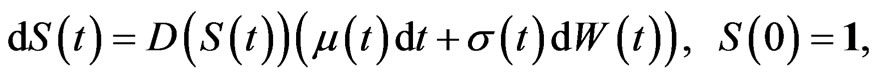 (4)
(4)
respectively. Here, the vector
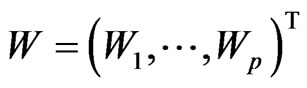
is a 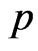 -dimensional standard Brownian motion independent of
-dimensional standard Brownian motion independent of 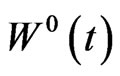 on a probability space
on a probability space
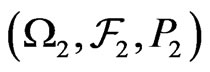 . We use superscript “
. We use superscript “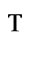 ” to denote the transpose of a vector or matrix throughout this paper. The vector
” to denote the transpose of a vector or matrix throughout this paper. The vector
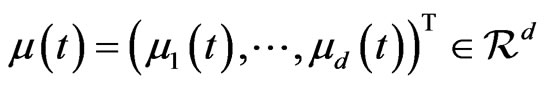
is the appreciation rate, the matrix 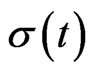 is the
is the
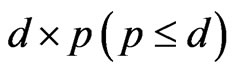
volatility with
 ,
,
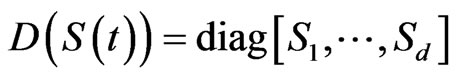
and
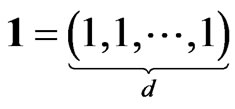 .
.
Assume that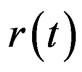 ,
,  and
and 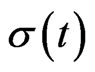 are deterministic functions of t. Let
are deterministic functions of t. Let 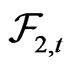 denote the natural filtration generated by
denote the natural filtration generated by
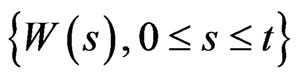 .
.
Let
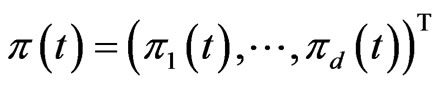
represent the amount invested in the risky asset at time . When both optimal investment and proportional reinsurance are included in our problem formulation, incorporating the strategy
. When both optimal investment and proportional reinsurance are included in our problem formulation, incorporating the strategy
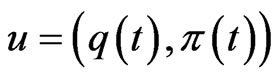
in (2), the dynamics of the resulting wealth process 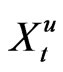 follows
follows
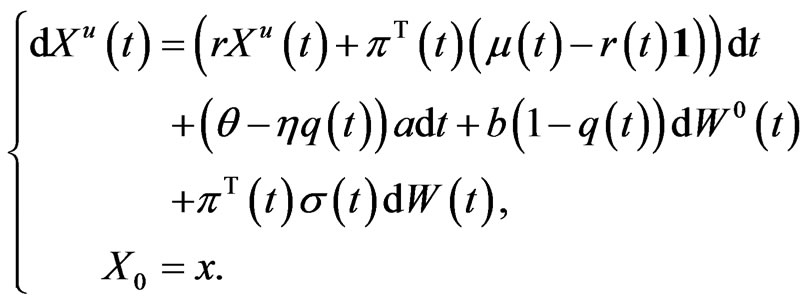
We denote
 .
.
Set
 with
with
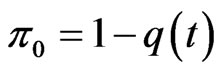 .
.
The strategy
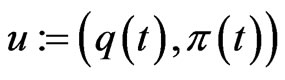
(equivalently,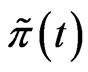 ),
),
 is said to be
is said to be  if 1) it is
if 1) it is  -progressively measurable2)
-progressively measurable2)
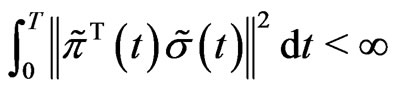
 -almost surely3)
-almost surely3)
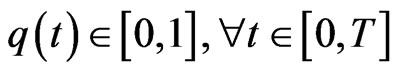 .
.
Let  be the class of all such
be the class of all such  strategies. We assume that the following assumption is satisfied.
strategies. We assume that the following assumption is satisfied.
Assumption 2.1. There exist constants  and
and  such that
such that


 (5)
(5)
where
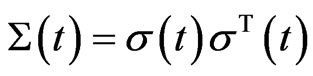 .
.
Problem (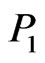 ). Given the wealth process (5), find an admissible strategy
). Given the wealth process (5), find an admissible strategy 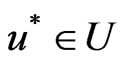 such that the expectation of the final wealth utility defined by
such that the expectation of the final wealth utility defined by
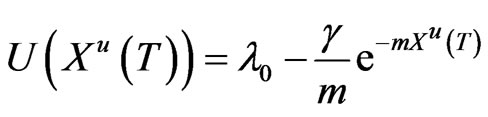 (6)
(6)
is maximized, where the constant  is the risk aversion parameter (see Pratt [21]).
is the risk aversion parameter (see Pratt [21]).
Now we specify the dynamic risk and impose it as the risk constraint for the optimal investment and reinsurance problem. Suppose that the portfolio is adjusted frequently over time so that the interval from time 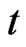 to time
to time 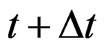 is small, where
is small, where . Here,
. Here, 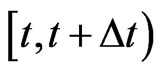 is the risk evaluation horizon, or the risk horizon for short. We consider the loss from time
is the risk evaluation horizon, or the risk horizon for short. We consider the loss from time 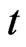 to
to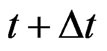 . Denote
. Denote
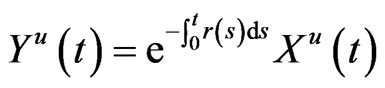
and
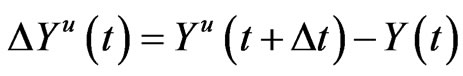 .
.
Suppose that
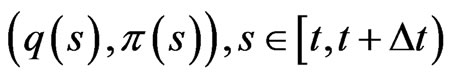
is unchanged in the interval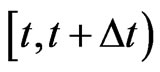 , i.e.,
, i.e.,
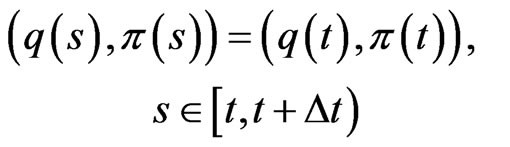 .
.
We have
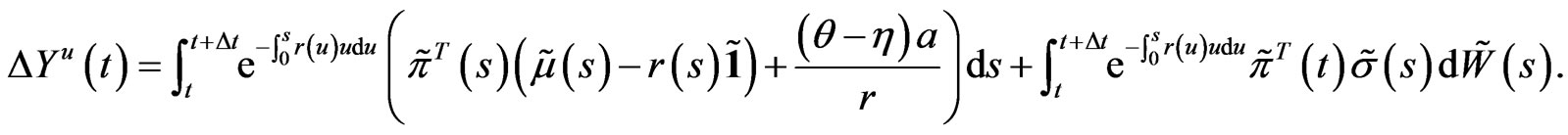
It follows that
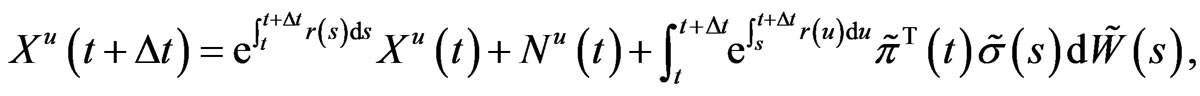 (7)
(7)
where
 (8)
(8)
Then, the mean and variance of 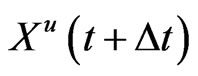 are, respectively, given by
are, respectively, given by
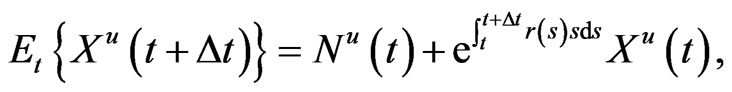 (9)
(9)
and
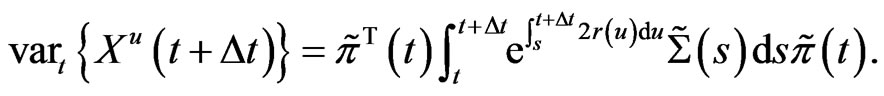 (10)
(10)
Let 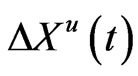 denote the discounted loss
denote the discounted loss
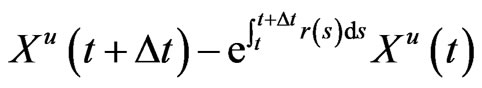 .
.
It follows from (10) and (9) that
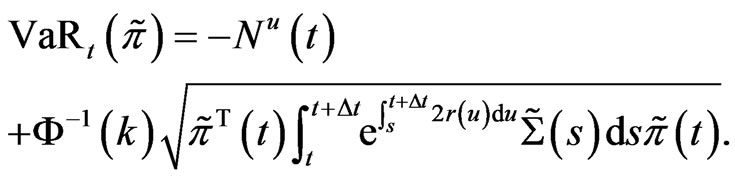 (11)
(11)
Let the maximal risk be less than or equal to , i.e.,
, i.e.,
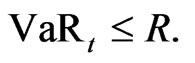 (12)
(12)
Then, the portfolio constraint is
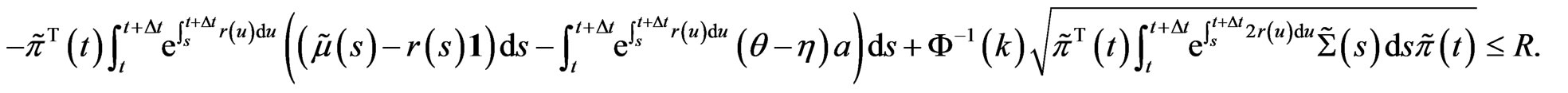 (13)
(13)
With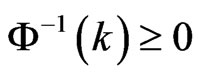 , namely,
, namely, 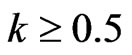 , the constraint (13) defines a convex set. In this work, we assume that
, the constraint (13) defines a convex set. In this work, we assume that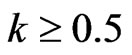 .
.
3. Deterministic Reduction
When the market is 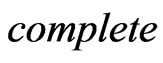 in the sense that
in the sense that 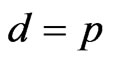 and no constraint is imposed on the strategy, Bai and Guo [15] investigate the problem with short-selling constraint. However, when the strategy is constrained in a general closed convex set due to the presence of the dynamic risk constraint, it is not known if there exists a smooth solution to the associated HJB equation or not. In fact, even if we could show the existence of a smooth solution, this second order nonlinear PDE is difficult to solve, even numerically.
and no constraint is imposed on the strategy, Bai and Guo [15] investigate the problem with short-selling constraint. However, when the strategy is constrained in a general closed convex set due to the presence of the dynamic risk constraint, it is not known if there exists a smooth solution to the associated HJB equation or not. In fact, even if we could show the existence of a smooth solution, this second order nonlinear PDE is difficult to solve, even numerically.
For the stochastic optimal control problem considered in this paper, since the utility function is an exponential function. We will show that it can be reduced to a deterministic optimal control problem via a suitable decomposition. It is further reduced, by the control parametrization technique [22], to a deterministic finite-dimensional problem. A numerical solution of this deterministic optimization problem can be obtained using existing optimization software packages, such as NLPQLP ([18-20]).
We first present a transformation theorem that links the original stochastic optimal control problem with the deterministic optimal control problem. Before stating the theorem, we need to introduce the following notations. For any path , denote
, denote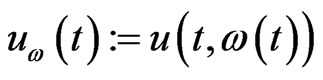 . Let
. Let

Theorem 3.1 Suppose that
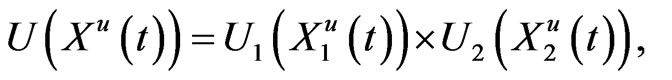
where 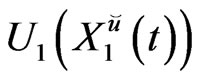 is deterministic for all
is deterministic for all , and
, and 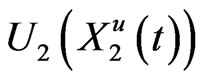 is a
is a  martingale. Then,
martingale. Then,
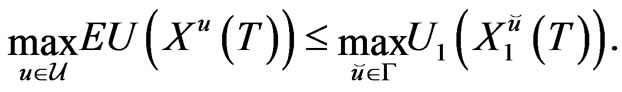 (14)
(14)
Furthermore, denote
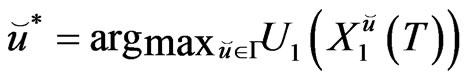
and let
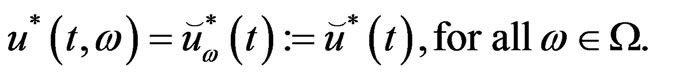
If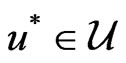 , then
, then
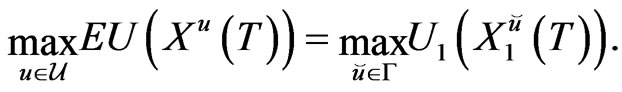 (15)
(15)
Proof. From the properties of Martingale, we have
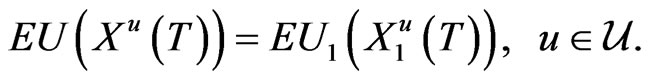
As
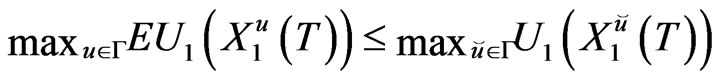 it follows that (14) holds.
it follows that (14) holds.
From the notation of , we see that, as
, we see that, as ,
,
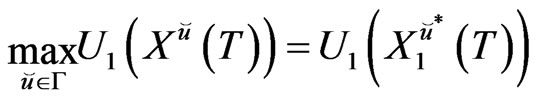 (16)
(16)
and
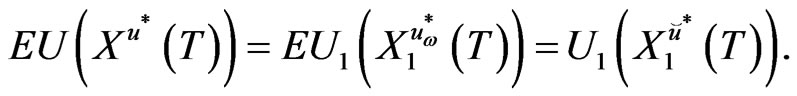 (17)
(17)
It follows from (16) and (17) that
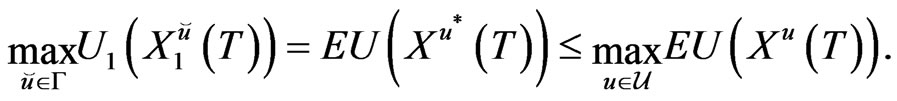
This, together with (14), implies the validity of (15).
This theorem shows that if the decomposition holds, the optimal strategy is the same for all paths, because the parameters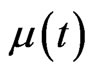 ,
, 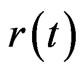 and
and 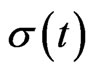 are deterministic.
are deterministic.
Remark 3.1 Suppose that the parameters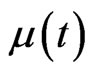 ,
,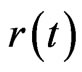 and
and 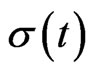 are
are 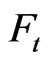 -progressive measurable. Since
-progressive measurable. Since
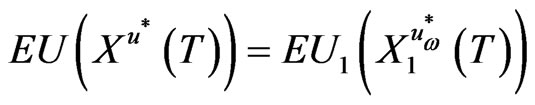 the stochastic optimal control problem is reduced to the deterministic optimal control problem with every path.
the stochastic optimal control problem is reduced to the deterministic optimal control problem with every path.
3.1. The Equivalent Problem
In this subsection, we will show that our problem satisfies the decomposition assumption specified in Theorem 3.1.
Rewrite the dynamics (5) as:
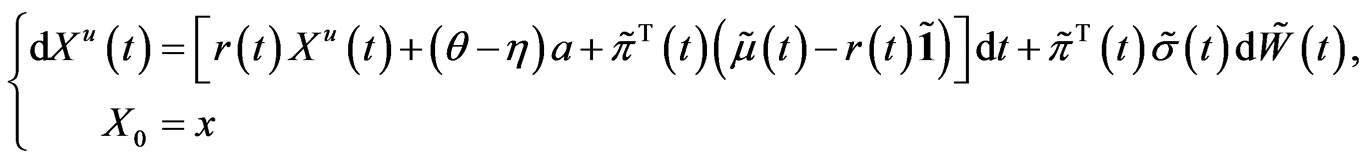
where

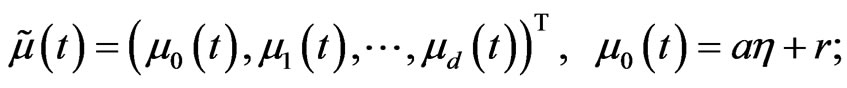
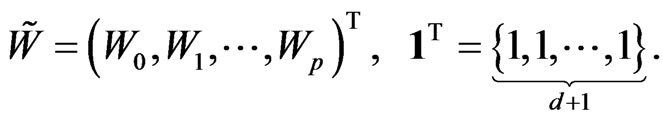 (18)
(18)
Applying Itô’s differentiation rule to (18), we obtain
 (19)
(19)
Thus,
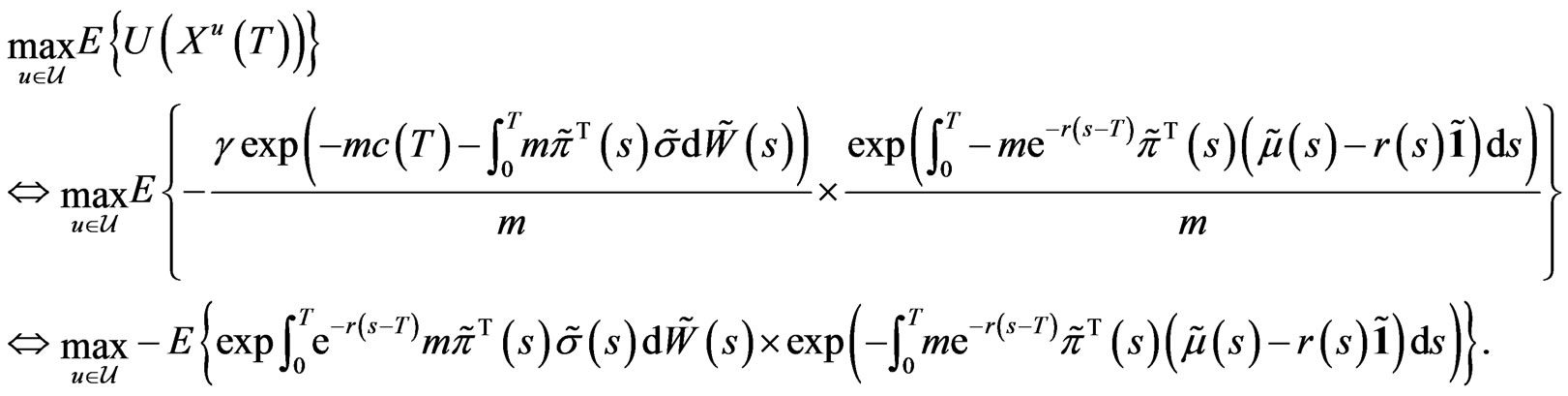 (20)
(20)
Denoting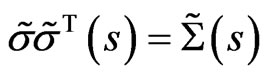 , we have
, we have
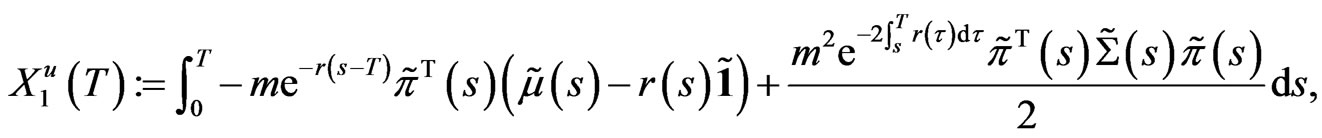
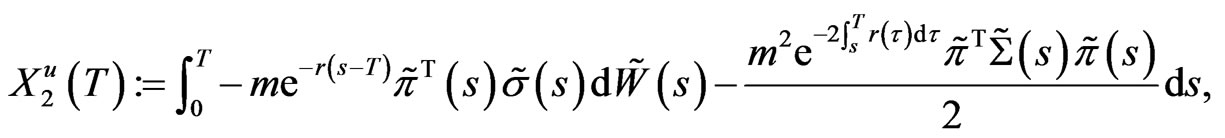 (21)
(21)
and
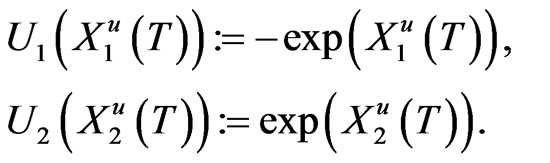
Obviously, 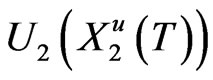 is a Martingale under Assumption 2.1. By Theorem 3.1, the original problem can be reduced to the deterministic optimal control problem
is a Martingale under Assumption 2.1. By Theorem 3.1, the original problem can be reduced to the deterministic optimal control problem
 (22)
(22)
Notice that (22) is also equivalent to the following problem.
Problem (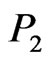 ). Find
). Find 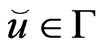 such that
such that
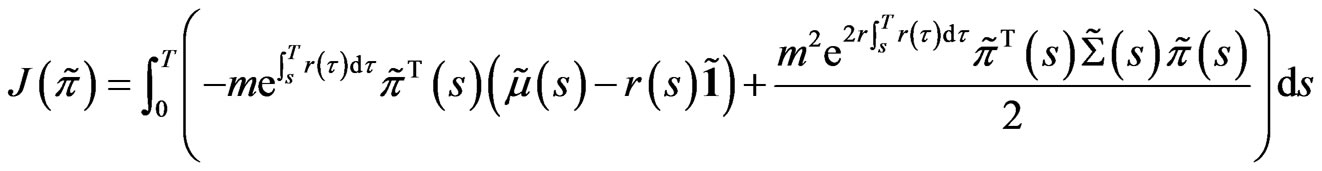 (23)
(23)
is minimized, subject to
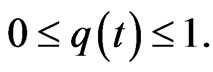 (24)
(24)
In the next section, we will show that Problem 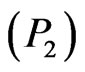 admits an optimal solution.
admits an optimal solution.
3.2. Existence of Optimal Solutions
From Theorem 3.1, we see that the optimal strategy is the same for almost all the sample paths. Thus, it suffices to seek a deterministic control strategy for Problem 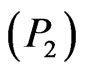 if all the required assumptions are satisfied.
if all the required assumptions are satisfied.
Let 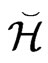 denote the class of all
denote the class of all 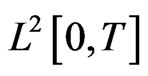 functions.
functions.
If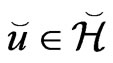 , define
, define

For Problem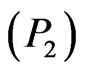 , it is easily seen that if
, it is easily seen that if , we have that
, we have that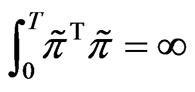 , and then
, and then . Thus, we can consider the following Problem
. Thus, we can consider the following Problem 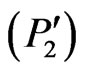 with a smaller control set
with a smaller control set , instead of Problem
, instead of Problem 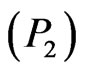 with
with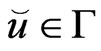 .
.
Note that 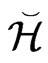 is a Hilbert space equipped with the inner product of
is a Hilbert space equipped with the inner product of  and
and 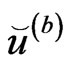 defined by
defined by
 (25)
(25)
Let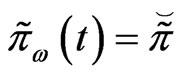 . Then, we have the following result.
. Then, we have the following result.
Theorem 3.2 Consider Problem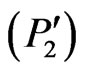 , where the function
, where the function 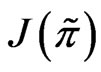 is defined by
is defined by
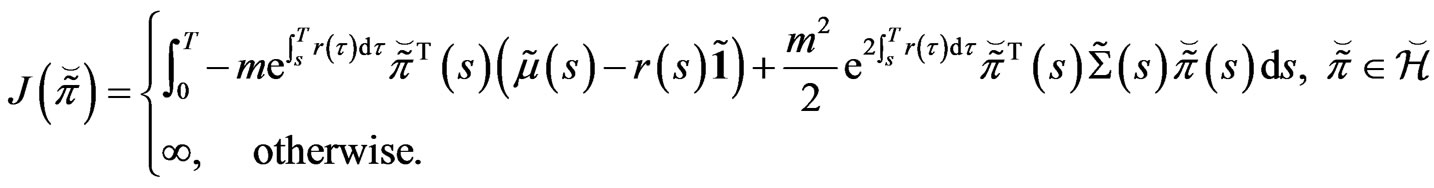
Then, the following properties are satisfied.
1) 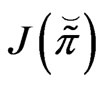 is convex;
is convex;
2) 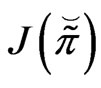 is coercive, i.e.,
is coercive, i.e.,
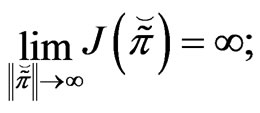
and
3) 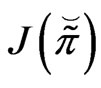 is lower-semicontinuous, i.e.,
is lower-semicontinuous, i.e.,
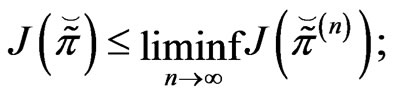 (26)
(26)
for every  and
and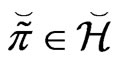 , with
, with
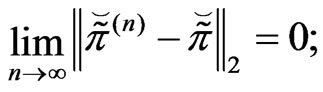
4) There exists a 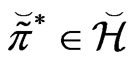 such that
such that
 .
.
Proof. 1) The convexity is obvious, since

and
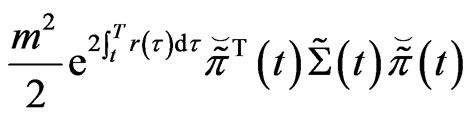
are concave.
1) From Assumption 2.1, we obtain
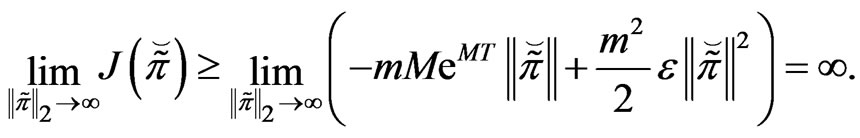 (27)
(27)
3)
 (28)
(28)
Also,
 (29)
(29)
Thus, 3) holds.
4) From Ekeland and Temam [23], a
a  such that
such that
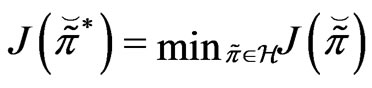 .
.
Proposition 3.1 The optimal strategy

is given by
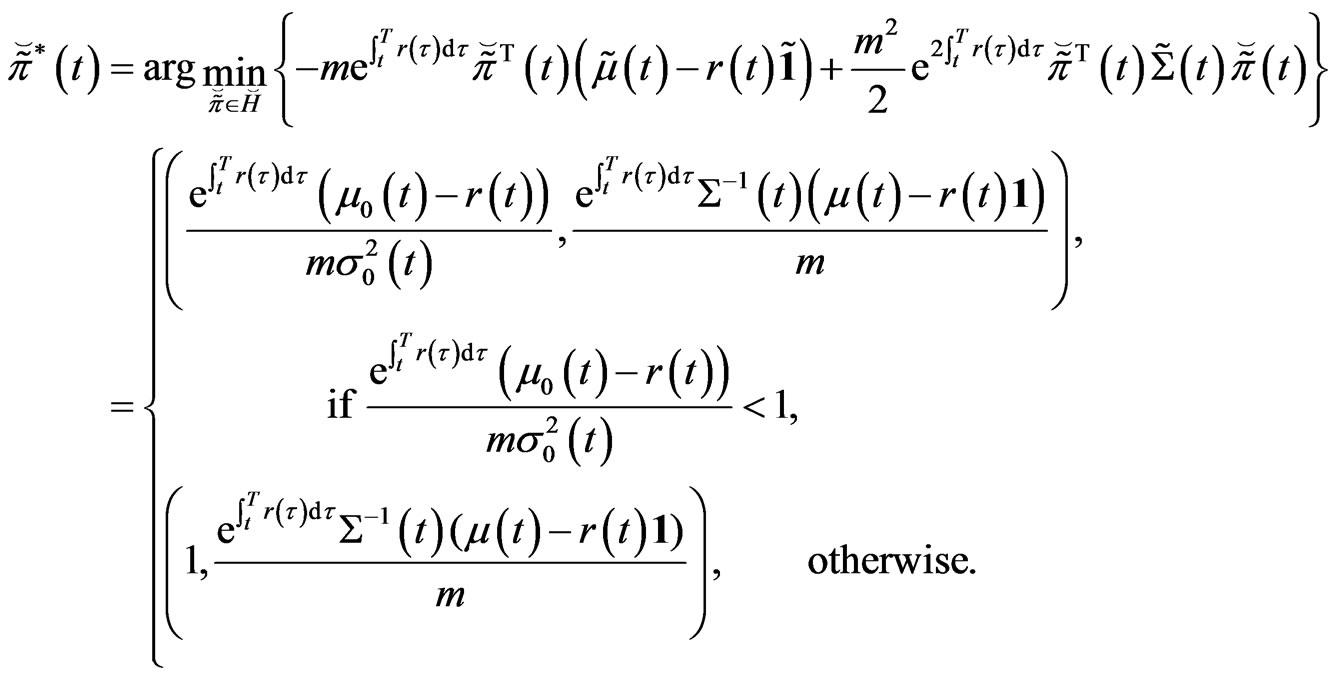
with 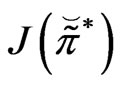 being its value function.
being its value function.
Proof. From the expression of , it is easily seen that the pointwise optimal strategy is just the optimal strategy at time
, it is easily seen that the pointwise optimal strategy is just the optimal strategy at time . The result in Bai and Guo [15] is a special case with constant parameters.
. The result in Bai and Guo [15] is a special case with constant parameters.
Using an argument similar to that given for Theorem 3.1, we can concentrate on finding a deterministic strategy from
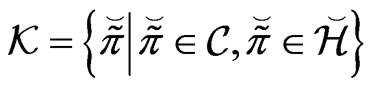 .
.
Corollary 3.1 Define
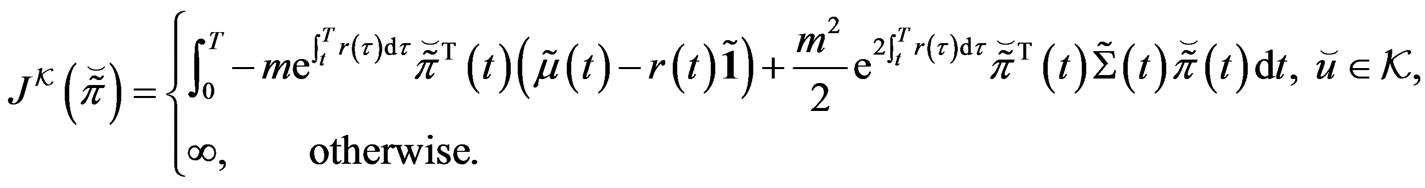
Then, there exists a 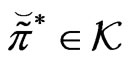 such that
such that
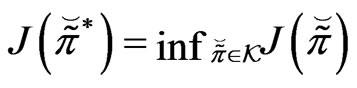 .
.
Proof. The proof is similar to that given for the proof of Theorem 3.1 and hence is omitted here.
Let the strategy in Proposition 3.1 be constrained to lie in a closed convex set . Then, the following result holds.
. Then, the following result holds.
Proposition 3.2 The optimal strategy is given by
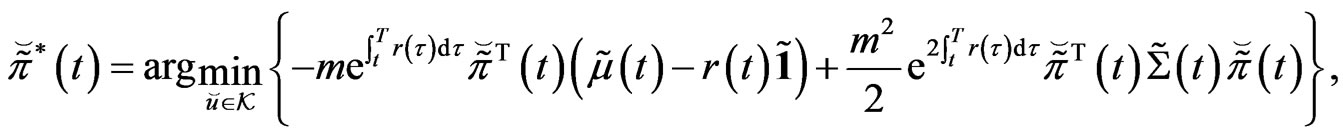 (30)
(30)
with  being its value function.
being its value function.
Although it is difficult to obtain an explicit solution to (30), we can solve this finite-dimensional optimization problem numerically. This is much simpler than dynamic programming, which involves solving a second order nonlinear PDE with constraint. It is also much simpler than the Martingale approach for which it is required to consider the replicate portfolio with constraint.
4. Numerical Experiments
We will develop a numerical method for constructing an approximation of 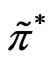 and then calculating
and then calculating . In solving the deterministic constrained optimization problem, we use the control parametrization method (see [18-20]). Let the time horizon
. In solving the deterministic constrained optimization problem, we use the control parametrization method (see [18-20]). Let the time horizon 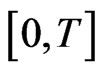 be partitioned into
be partitioned into 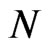 subintervals, and let
subintervals, and let 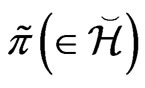 be approximated as a piecewise constant function, given by
be approximated as a piecewise constant function, given by
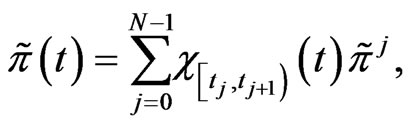 (31)
(31)
where  and
and  is the indicator function defined by
is the indicator function defined by
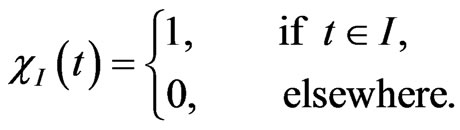
For each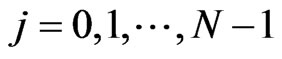 ,
,  is a vector specifying the value of
is a vector specifying the value of 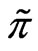 on the sub-interval
on the sub-interval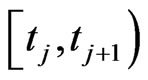 . Such a strategy should be chosen such that (23) is minimized subject to the dynamics (24). Then, Problem
. Such a strategy should be chosen such that (23) is minimized subject to the dynamics (24). Then, Problem 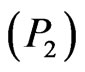 can be solved as an optimization problem, and various optimization software packages, such as NLPQLP (see [18-20]), can be used for this purpose.
can be solved as an optimization problem, and various optimization software packages, such as NLPQLP (see [18-20]), can be used for this purpose.
Consider a complete market where the number 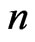 of stocks is equal to the dimension of the driving geometric Brownian motion. The proportional reinsurance
of stocks is equal to the dimension of the driving geometric Brownian motion. The proportional reinsurance  is the only constraint. In this market, Proposition 3.1 has given the explicit expression of
is the only constraint. In this market, Proposition 3.1 has given the explicit expression of  and
and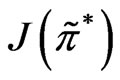 . Here, two sets of parameters are used to show that when the trading interval approaches to zero the solutions converge to those in [15].
. Here, two sets of parameters are used to show that when the trading interval approaches to zero the solutions converge to those in [15].
Case I (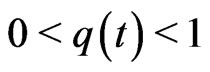 when the reinsurance constraint is inactive). The model parameters are:
when the reinsurance constraint is inactive). The model parameters are:
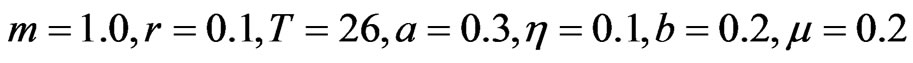
and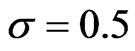 . Figures 1 and 2 plot the risky investment and the proportional reinsurance, respectively.
. Figures 1 and 2 plot the risky investment and the proportional reinsurance, respectively.
Case II (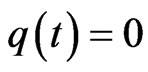 when the reinsurance constraint is active).
when the reinsurance constraint is active).
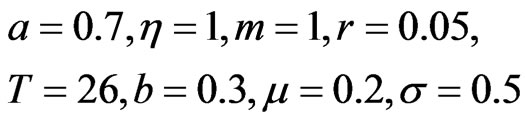 .
.
the proportional reinsurance  for cases with or without risk constraint. In Figure 3, the risky investment under the risk control is compared with the risky investment without control.
for cases with or without risk constraint. In Figure 3, the risky investment under the risk control is compared with the risky investment without control.
To show the effectiveness of the method, we also solve the problem under this assumption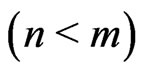 . Here, we assume that there is one risky asset, and the Brownian Motion is two-dimensional. The following parameters are used:
. Here, we assume that there is one risky asset, and the Brownian Motion is two-dimensional. The following parameters are used:
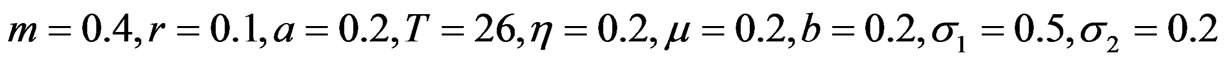
Figures 4 and 5 plot the risky investment and the proportional reinsurance, respectively.
In this example, parameters are assumed to be constants, taking the values:
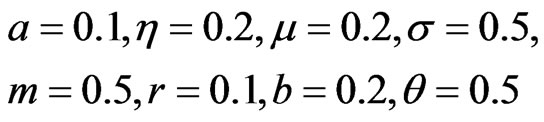
and . Figure
. Figure  compares the risky investment
compares the risky investment
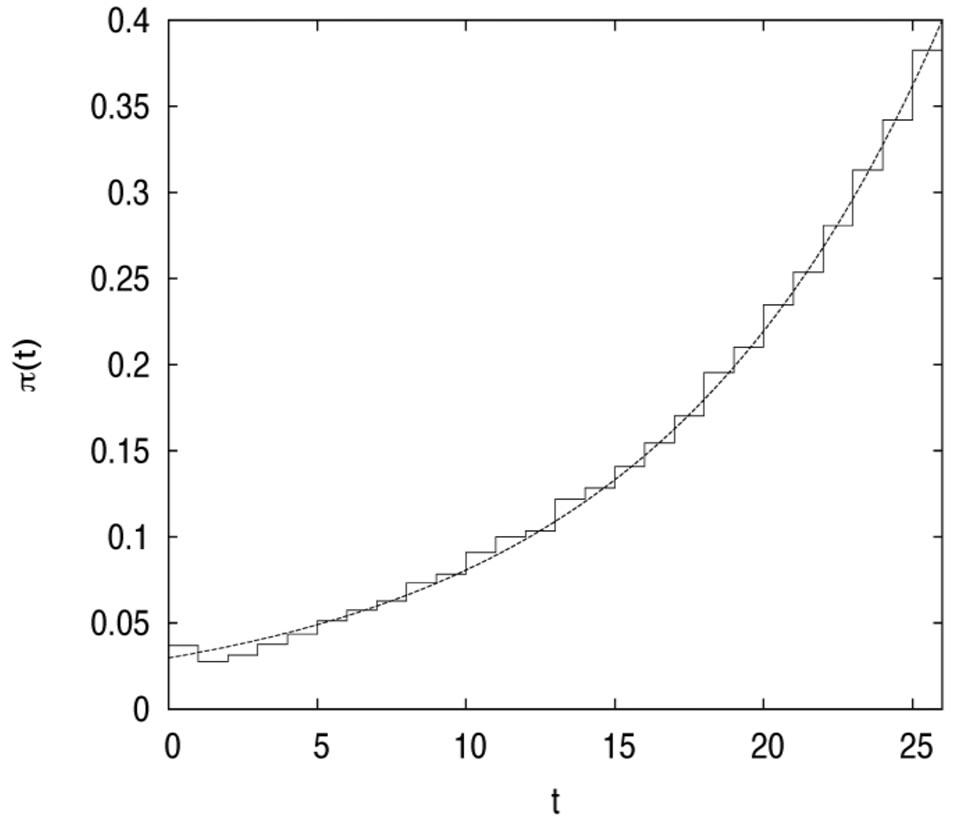
Figure 1. The risky investment in case 1.
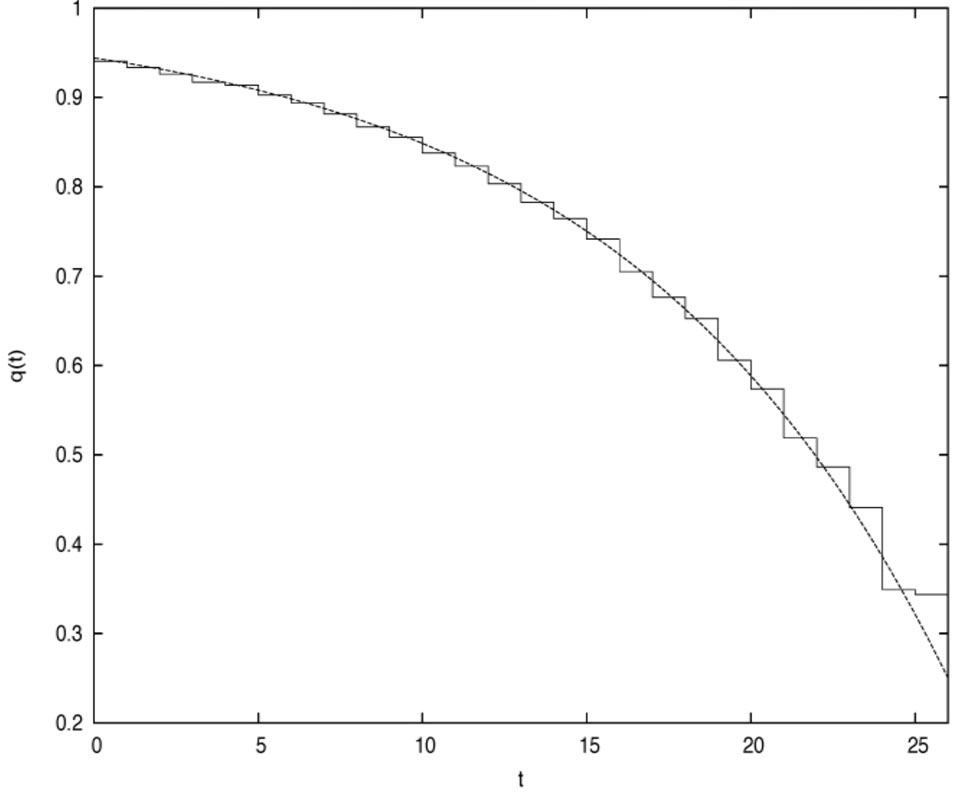
Figure 2. The proportional reinsurance in case 1.
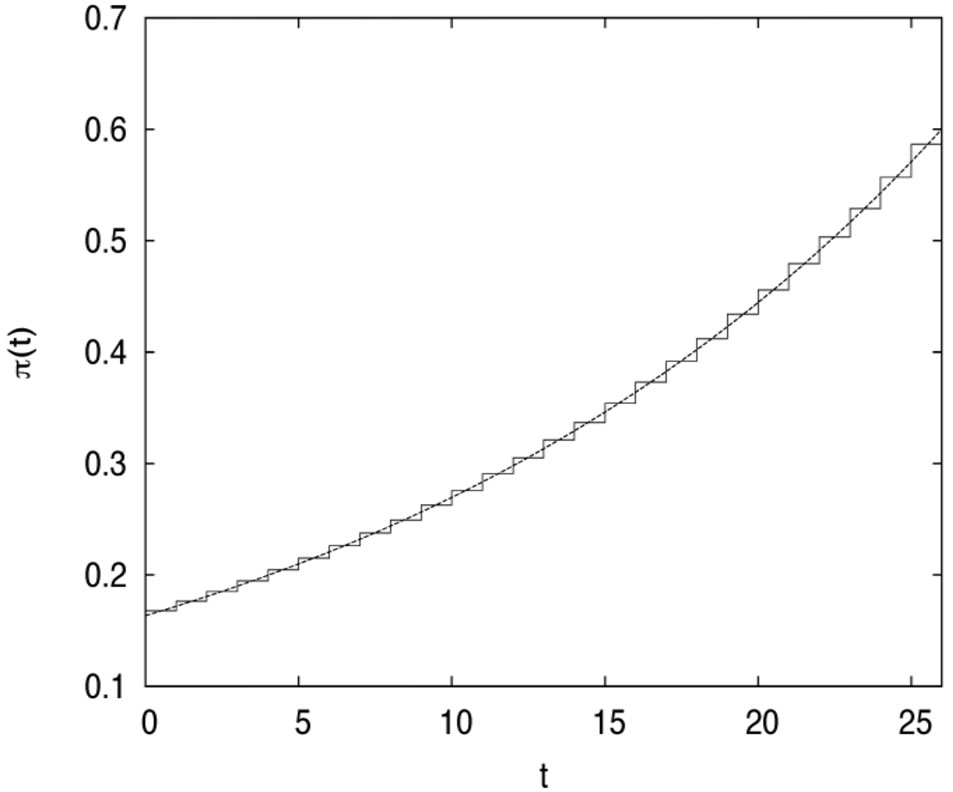
Figure 3.The risky investment in case 2.
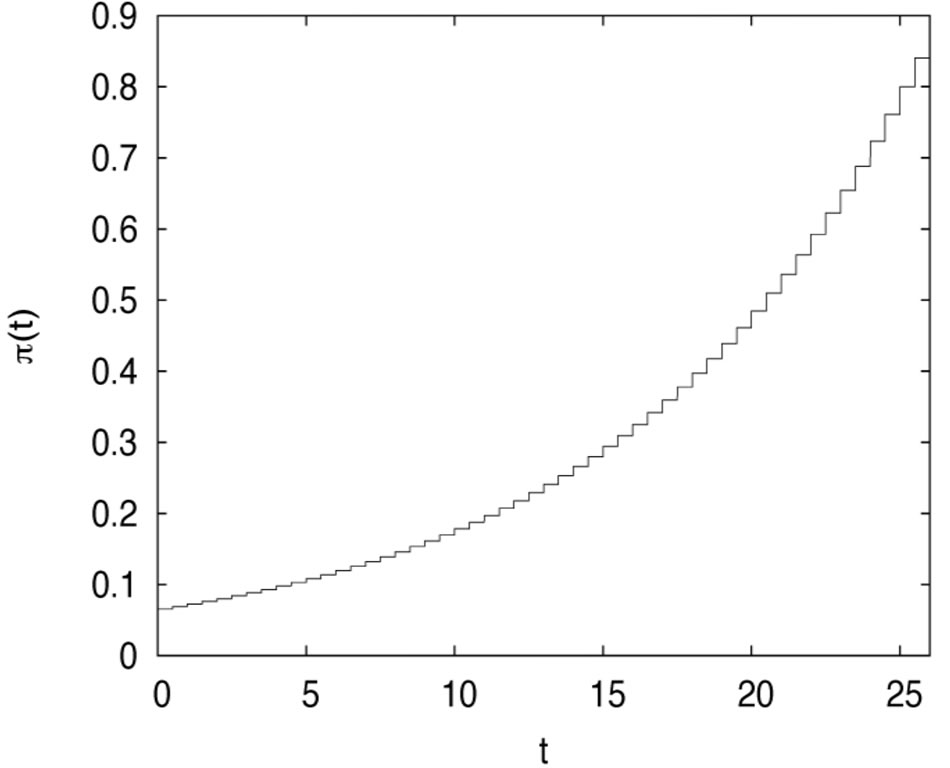
Figure 4. The optimal risky investment in the incomplete market (n < m).
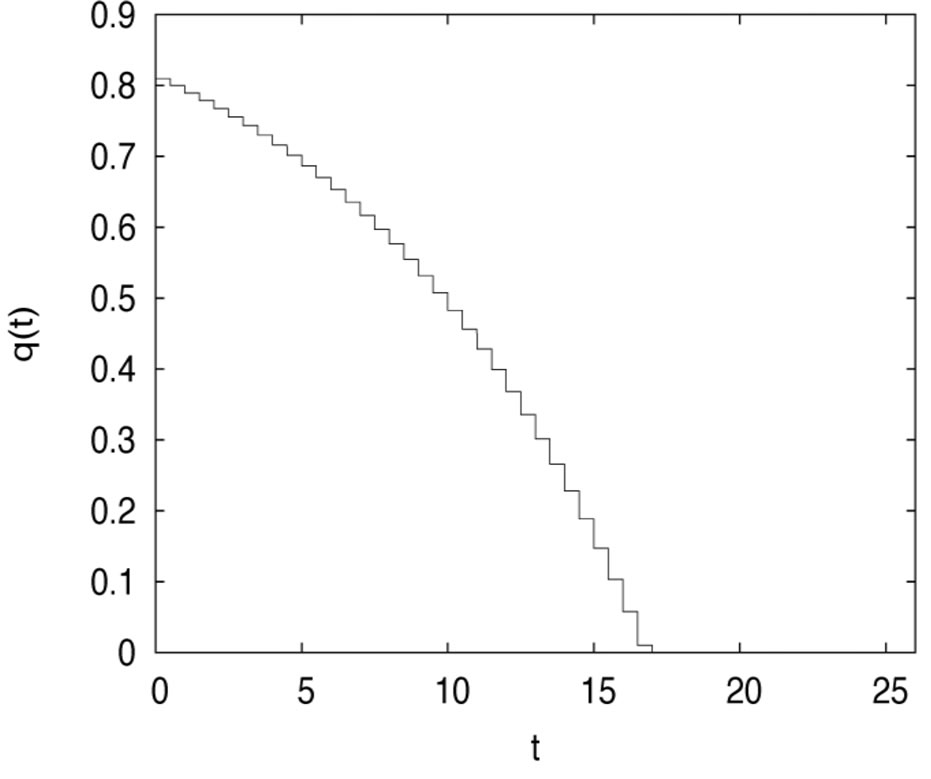
Figure 5. The optimal proportional reinsurance in the incomplete market (n < m).
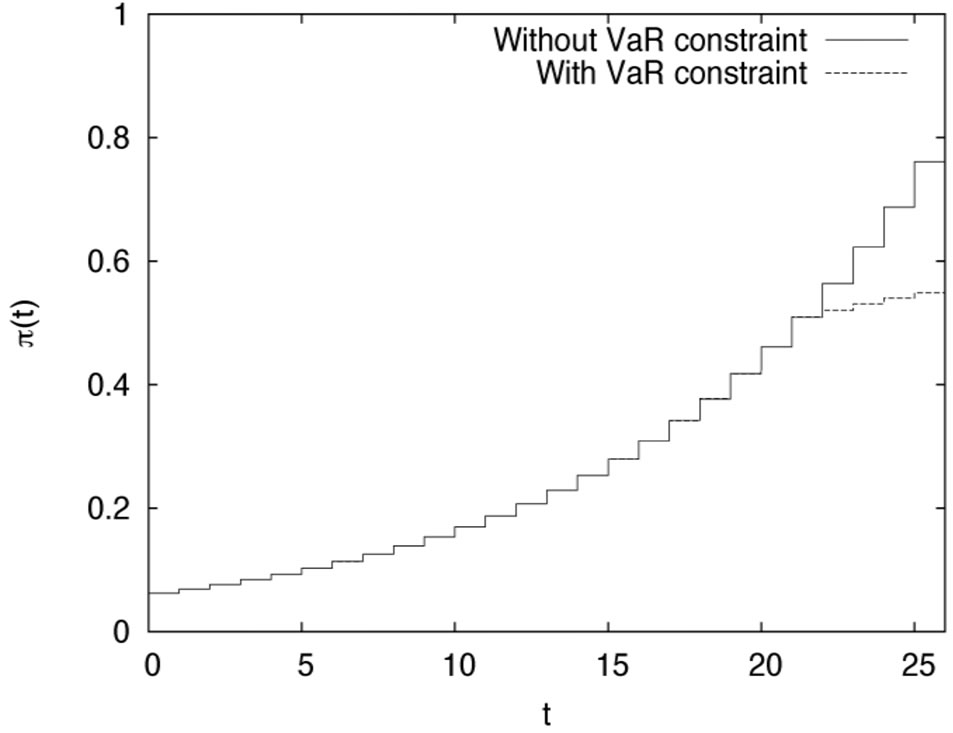
Figure 6. The risky investment compared in the cases: with and without constraint.
in the constrained case with the risky investment without VaR constraint. It is easily seen from Figure 6 that if VaR is active, the risky investment should be cut down consistent with the purpose of the risk management. Figure 7 plots the proportional reinsurance, also for both cases. If the constraint is active, the proportional reinsurance should be increased, when compared with the case of no constraint. We can show its validity under the assumption that 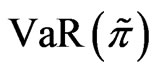 is increasing with
is increasing with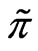 . To be more specific, let the optimal strategy for the case without constraint and that with constraint be denoted by
. To be more specific, let the optimal strategy for the case without constraint and that with constraint be denoted by 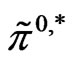 and
and , respectively. Then,
, respectively. Then,
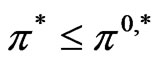 ,
, .
.
In fact, to satisfy the constraint, we require that either
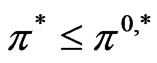 or
or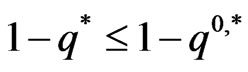 .
.
without loss of generality, assume that . If
. If
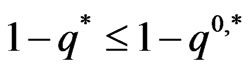 then it is clear that the result holds. Otherwise,
then it is clear that the result holds. Otherwise,
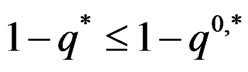 which means that
which means that  is in the constraint set. However,
is in the constraint set. However,
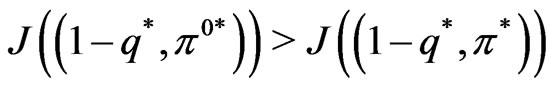 which is a contradiction to the fact that
which is a contradiction to the fact that  is optimal. Thus, it follows that
is optimal. Thus, it follows that
 ,
, 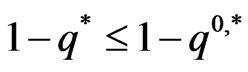
if 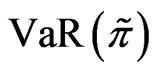 is increasing with
is increasing with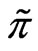 . In fact, this condition is reasonable as the time horizon
. In fact, this condition is reasonable as the time horizon 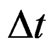 is small. From Figure 8, we see that VaR is stabilized once the risk constraint is active.
is small. From Figure 8, we see that VaR is stabilized once the risk constraint is active.
5. Conclusion
In this work, we considered the optimal investment and proportional reinsurance problem with VaR as the dynamic risk constraint. By employing a decomposition approach, we transformed the stochastic optimal control problem into an equivalent deterministic optimal control problem. This equivalent problem is solvable by existing optimal control techniques. It is observed that when the risk constraint is active, the insurer should decrease the investment on risky asset, while increasing the proportional reinsurance. This is consistent with the risk management. The method proposed in this paper is effective for the case with or without constraint. It is also effective in complete and incomplete market(i.e., the number of risky assets is fewer than the dimension of uncertainty). Our approach appears possible for extension to the case when the parameters are 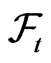 -progressively measurable.
-progressively measurable.
6. Acknowledgements
The first author and second author gratefully ac
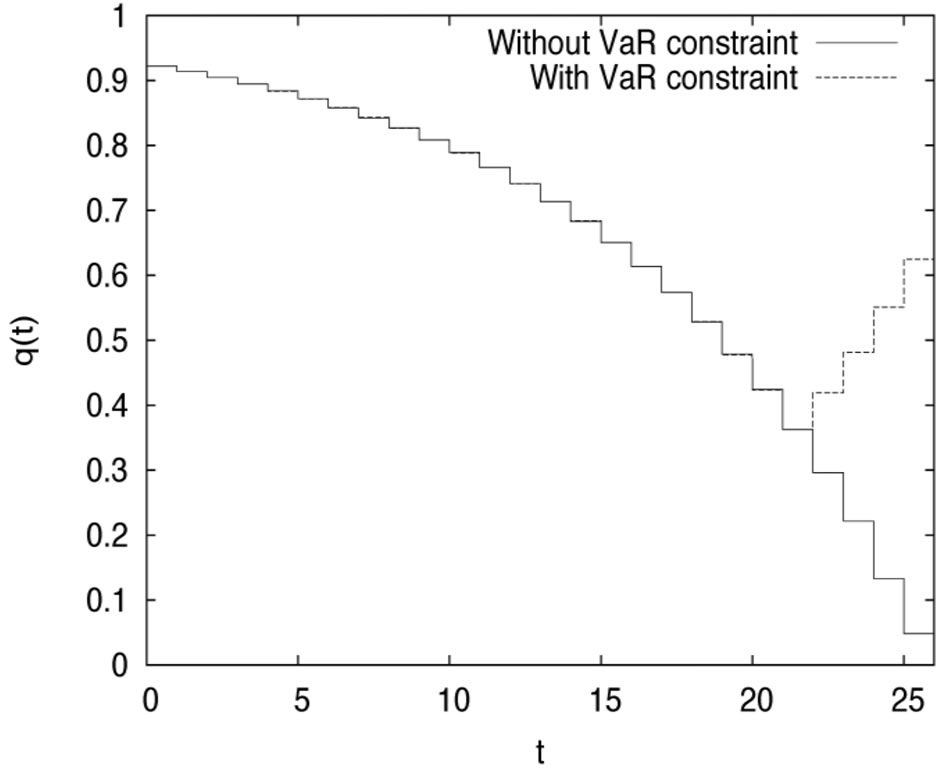
Figure 7. The proportional reinsurance compared in the cases: with and without constraint.
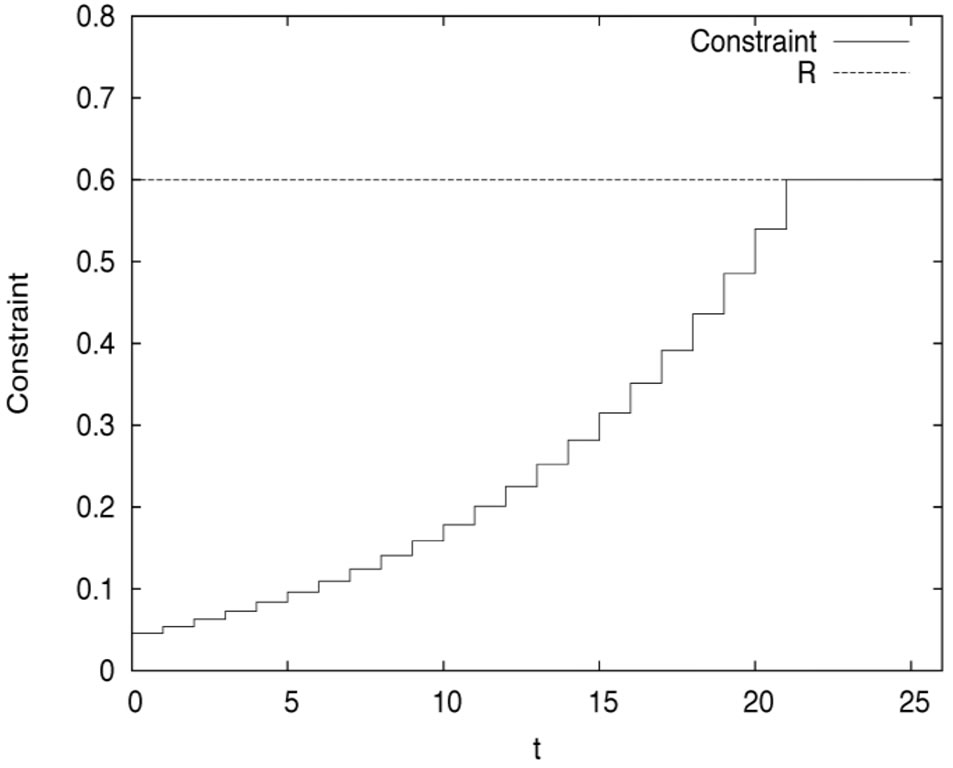
Figure 8. VaR level.
knowledge the financial support from the Research Grants Council of HKSAR (CityU 500111). The first author is thankful for the support of Natural and the Science National Foundation of China (11301559).
REFERENCES
- S. Browne, “Optimal Investment Policies for a Firm with a Random Risk Process: Exponential Utility and Minimizing the Probability of Ruin,” Mathematics of Operations Research, Vol. 20, No. 4 1995, pp. 937-958. http://dx.doi.org/10.1287/moor.20.4.937
- R. Kostadinova, “Optimal Investment for Insurers When the Stock Price Follows Anexponential Levy Process,” Insurance: Mathematics and Economics, Vol. 41, No. 2, 2007, pp. 250-263. http://dx.doi.org/10.1016/j.insmatheco.2006.10.018
- J. Ma and X. Sun, “Ruin Probabilities for Insurance Models Involving Investments,” Scandinavian Actuarial Journal, Vol. 2003, No. 3, 2003, pp. 217-237. http://dx.doi.org/10.1080/03461230110106381
- D. S. Promislow and V. R. Young, “Minimizing the Probability of Ruin When Claims Follow Brownian Motion with Drift,” North American Actuarial Journal, Vol. 9, No. 3, 2005, pp. 109-128.
- D. S. Promislow and V. R. Young, “Minimizing the Probability of Ruin When Claims Follow Brownian Motion with Drift,” North American Actuarial Journal, Vol. 9, No. 3, 2005, pp. 109-128.
- H. Schmidli, “Optimal Proportional Reinsurance Policies in a Dynamic Setting,” Scandinavian Actuarial Journal, Vol. 2001, No. 1, 2001, pp. 55-68. http://dx.doi.org/10.1080/034612301750077338
- H. Schmidli, “On Minimizing the Ruin Probability by Investment and Reinsurance,” The Annals of Applied Probability, Vol. 12, No. 3, 2002, pp. 890-907. http://dx.doi.org/10.1214/aoap/1031863173
- M. Taksar and C. Markussen, “Optimal Dynamic Reinsurance Policies for Larg Insurance Portfolios,” Finance and Stochastics, Vol. 7, No. 1, 2003, pp. 97-121. http://dx.doi.org/10.1007/s007800200073
- H. L. Yang and L. H. Zhang, “optimal Investment for Insurer with Jump Diffusion Risk Process,” Insurance: Mathematics and Economics, Vol. 37, No. 3, 2005, pp. 615-634. http://dx.doi.org/10.1016/j.insmatheco.2005.06.009
- J. Z. Liu, L. Bai and K. F. C. Yiu, “Optimal Investment with a Value-at-Risk Constraint,” Journal of Industrial and Management Optimization, Vol. 8, No. 3, 2012, pp. 531-547. http://dx.doi.org/10.3934/jimo.2012.8.531
- J. Z. Liu and K. F. C. Yiu, “Optimal Stochastic Differential Games with Var Constraints,” Discrete and Continuous Dynamical Systems-Series B, Vol. 18, No. 7, 2013, pp. 1889-1907. http://dx.doi.org/10.3934/dcdsb.2013.18.1889
- J. Z. Liu, K. F. C. Yiu and T. K. Siu, “Optimal Investment-Reinsurance with Dynamic Risk Constraint and Regime Switching,” Scandinavian Actuarial Journal, Vol. 2013, No. 4, 2013, pp. 263-285. http://dx.doi.org/10.1080/03461238.2011.602477
- J. Z. Liu, K. F. C. Yiu and K. L. Teo, “Optimal Portfolios with Stress Analysis and the in a Effect of a CVaR Constraint,” Pacific Journal of Optimization, Vol. 7, No. 1, 2010, pp. 83-95.
- K. F. C. Yiu, “Optimal Portfolio under a Value-at-Risk Constraint,” Journal of Economic Dynamics and Control, Vol. 28, No. 7, 2004, pp. 1317-1334. http://dx.doi.org/10.1016/S0165-1889(03)00116-7
- L. Bai and J. Guo, “Optimal Proportional Reinsurance and Investment with Multiple Risky Assets and NoShorting Constrain,” Insurance: Mathematics and Economics, Vol. 42, No. 3, 2008, pp. 968-975. http://dx.doi.org/10.1016/j.insmatheco.2007.11.002
- B. Hujgaard and M. Taksar, “Optimal Proportional Reinsurance Policies for Diffusion Models,” Scandinavian Actuarial Journal, Vol. 1998, No. 2, 1998, pp. 166-180. http://dx.doi.org/10.1080/03461238.1998.10414000
- H. Gerber, “An Introduction to Mathematical Risk Theory,” Richard D Irwin, Bloomsbury, 1979.
- R. C. Loxton, K. L. Teo and V. Rehbock, “Optimal Control Problems with Multiple Characteristic Time Points in the Objective and Constraints,” Automatica, Vol. 44, No. 11, 2008, pp. 2923-2929. http://dx.doi.org/10.1016/j.automatica.2008.04.011
- R. C. Loxton, K. L. Teo, V. Rehbock and K. F. C. Yiu, “Optimal Control Problems with Continuous Constraints on the State and the Control,” Automatica, Vol. 45, No. 10, 2009, pp. 2250-2257. http://dx.doi.org/10.1016/j.automatica.2009.05.029
- K. L. Teo, “Control Parametrization Enhancing Transform to Optimal Control Problems Nonlinear Analysis,” Vol. 63, No. 5-7, 2005, pp. 2223-2236. http://dx.doi.org/10.1016/j.na.2005.03.066
- J. W. Pratt, “Risk Aversion in the Small and in the Large,” Econometrica, Vol. 32, No. 1/2, 1964, pp. 122-136. http://dx.doi.org/10.2307/1913738
- K. L. Teo, J. Goh, and K. H. Wong, “A Unified Computational Approach to Optimal Control Problems,” Longman Scientific and Technical, Harlow, 1991.
- Ekeland and R. Temam, “Convex Analysis and Variational Problems,” Society for Industrial and Applied Mathematics, Philadelphia, 1976.
NOTES
1An incomplete market in Mathematical Finance corresponds to a setting, in which the controller has full information about many aspects of the system (the market), but various exogenously imposed constraints (taxation, transaction costs, bad credit rating, legislature etc.) prevent him/her from choosing the control (portfolio) outside a given constraint set. In fact, even without government-imposed portfolio constraints, financial markets will typically not offer tradeable assets corresponding to a variety of sources of uncertainty.

