Open Journal of Safety Science and Technology
Vol.3 No.4(2013), Article ID:40824,7 pages DOI:10.4236/ojsst.2013.34014
Numerical Modeling of the Thermal Behavior of Corrosion in Conduit in Transient Mode
1Laboratory of Electronics, Instrumentation and Signal Processing, Faculty of Sciences, El Jadida, Morocco
2Department of physics, Faculty of Sciences Semlalia, Marrakech, Morocco
Email: belattars@hotmail.com
Copyright © 2013 Naouar Laaidi, Sougrati Belattar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 23, 2013; revised September 23, 2013; accepted September 30, 2013
Keywords: Conduits; Corrosion; Rust; Transitory Mode; Infra-red Thermography; Finite Elements
ABSTRACT
The conduits in the buildings require a regular and permanent control, in order to avoid the risks of deterioration caused by corrosion. In this paper we present a thermal nondestructive testing method of concrete structures containing a conduit system, based on the analysis by infrared thermography principle and the numerical modeling in three dimensions. The aim is to study the detectability of these pipes in different situations versus time and to give a thermal characterization of the rust behavior in the transitory mode.
1. Introduction
The inspection of hidden corrosion at an early stage remains a main requirement in the maintenance and the repairs of deteriorated concrete structure. In fact, the degradation of concrete caused by corrosion is a very serious phenomenon which implies many risks and damages even the failure of concrete structure in civil engineering [1-3].
With the advances of NDT techniques, Infrared thermography has proven to be a good tool in detecting hidden corrosion [4], indeed (IR) thermography is widely used for non destructive evaluation of materials, especially in civil engineering and for the characterization of the heat loss in concrete structures. The thermals images obtained from infrared thermgraphy allow a quick mapping of surface structure by giving an overview of surface temperature [5-8].
In our latest works, the problem of corrosion was investigated in pipeline and oil conduit [9,10], also many defects which can occurs in concrete structure like void and cracks were studied [11,12]. The last two studies are combined on this innovative paper, hence in this work, the thermal behavior of rust layer is discussed and corrosion is detected due to a spatial-temporal structure analysis using a numerical simulation model based on FEM seen that modelling corrosion in concrete is important for predicting service life of concrete structure [13]. Therefore the use of FEM in the prediction of temperature evolution in concrete had a main importance in studying civil engineering structure.
The model of a parallelepiped concrete structure containing cylindrical conduits is adopted. This structure is supposed to be excited on the higher face by a heat flux, the lower face being maintained at a constant temperature and the other faces are supposed thermally insulated. The effects of thickness and position of the corrosion layer are studied.
2. Methods
Impulse thermography is based on the active heating of structure to be investigated, by using an internal or external heat source. The idea is that the heat transfer in materials is affected by a change in its thermal properties. Indeed, the difference between the transient temperature curves at surface above the region with defect and the one without defect is expected to provide information about the defect characteristics [14,15].
The present study gives numerical simulations of this technique using a finite element method. The aim is to verify the applicability of a thermal impulse for the analysis of the corrosion behavior in concrete structures.
When rust develops in the cylindrical structure, the steel cross-section decreases with the increase of the corrosion layer [16], which implies a lack of homogeneity in the steel section, and thus a weakening and modification physical properties (increased and reduced adhesion) [17], hence reducing the detection corrosion in this work. For reasons of simplicity, the changes in the thermal properties of materials that may occur due to chemical reactions involved in the corrosion process have been neglected in the detection of the layer thickness [18].
3. Modeling the Thermal Response
This study is undertaken on a concrete specimen (Figure 1) of (0.5 m × 0.5 m × 0.25 m), containing cylinders representing pipes, of 30.7 mm external diameter, ep = 2.9 mm wall thickness and 0.5 m length. Table 1 shows the corrosion parameters taken from [4,19] used in our model.
4. Governing Equations
The heat conduction equation of a specimen caused by Joule heating source Q is governed by the following thermal equation:
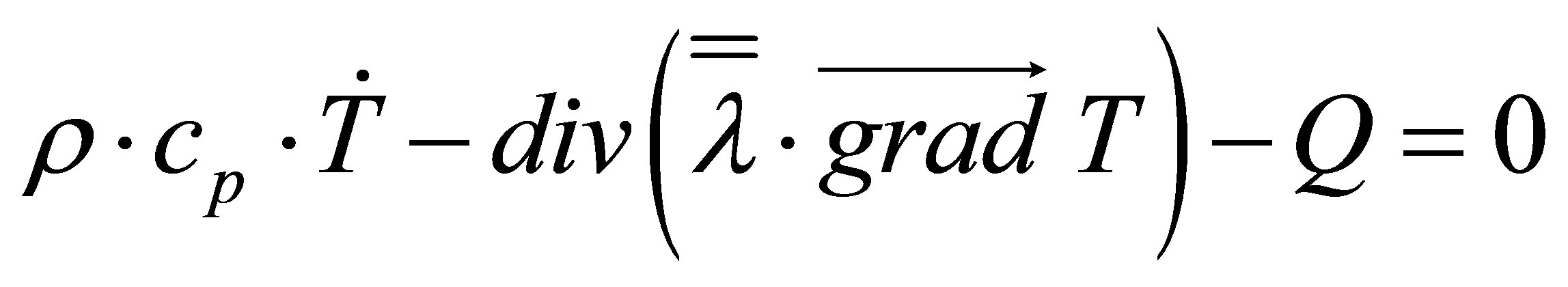 (1)
(1)
Where:
 : is the material density (kg/m3);
: is the material density (kg/m3);
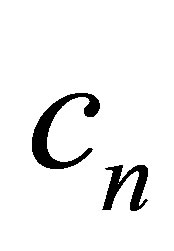 : is the Specific heat capacity (J/kg·K);
: is the Specific heat capacity (J/kg·K);

Figure 1. Finite element model of concrete specimen with defect.

Table 1. Thermal parameters of steel corrosion.
 : is the thermal tensor conductivity (W/m·K);
: is the thermal tensor conductivity (W/m·K);
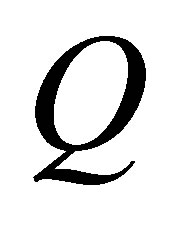 : is the voluminal source of heat (W/m3).
: is the voluminal source of heat (W/m3).
With the boundary conditions:
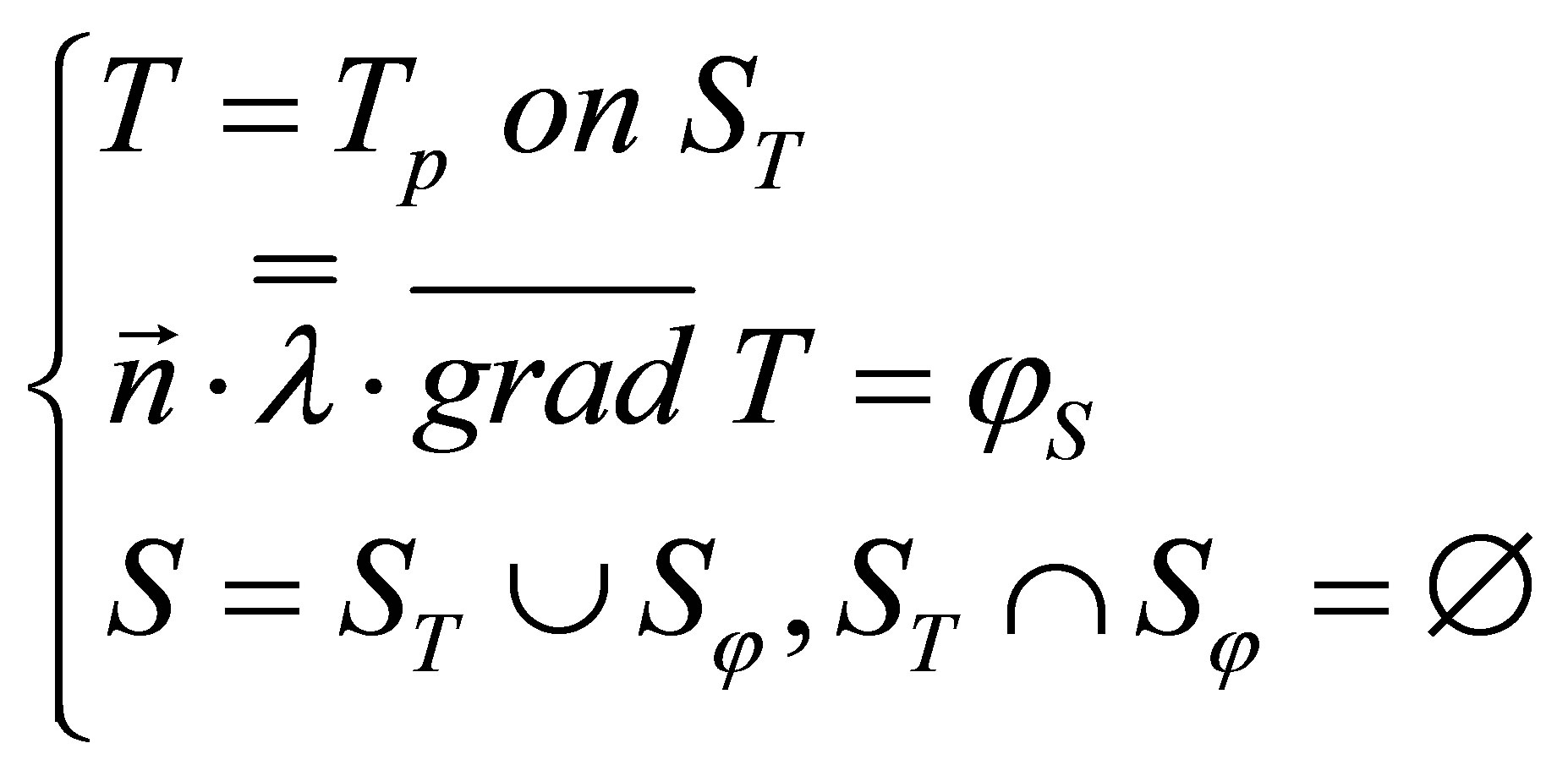 (2)
(2)
Where:
 : is the imposed temperature on a surface
: is the imposed temperature on a surface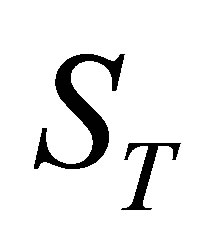 ;
;
 : is the imposed flow on a surface
: is the imposed flow on a surface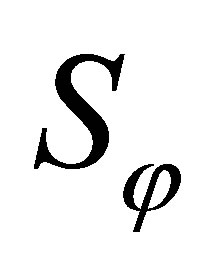 ;
;
S: is the surface of the solid;
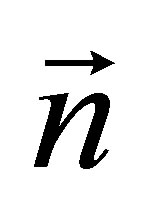 : is the unit vector perpendicular to S and directed towards outside.
: is the unit vector perpendicular to S and directed towards outside.
And the initial condition:
 (3)
(3)
5. Numerical Modelling
The analytical resolution of the Equation (1) is in general inaccessible. Therefore finite element method is used for an approached solution [20-22].
The method consists in using an approximation by finite elements of the unknown functions T to discretize the variational form of the Equation (1) and to transform it into system of algebric equations of the form:
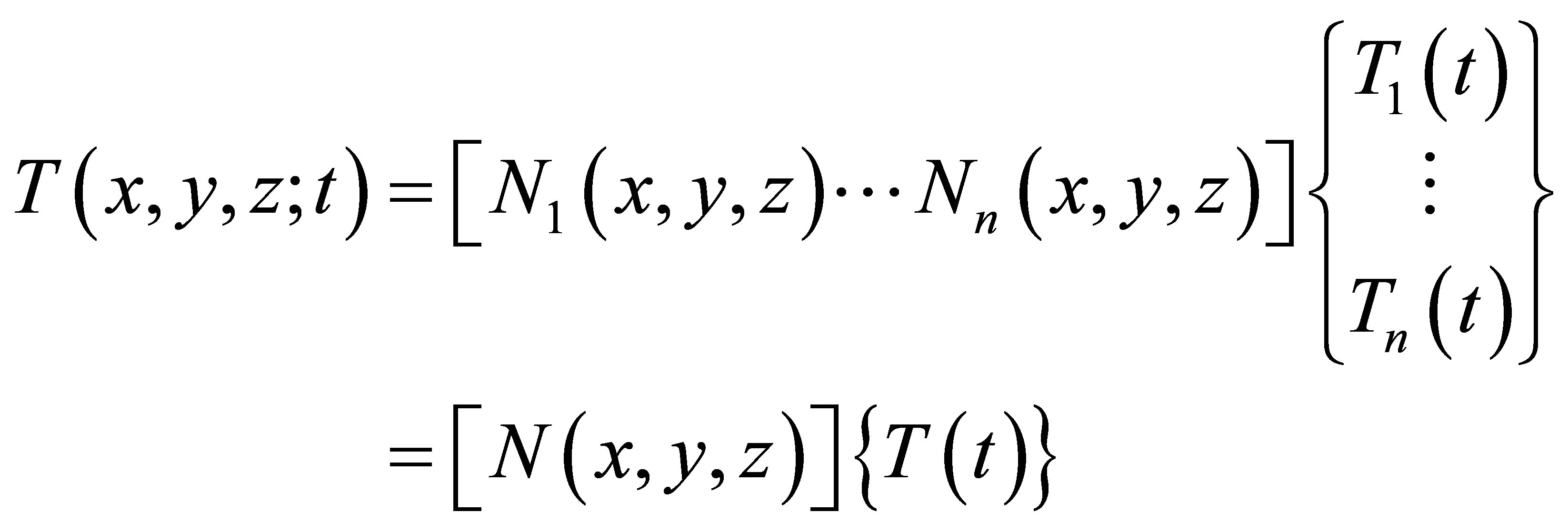 (4)
(4)
Where:
n: is the number of mesh nodes;
[N(x, y, z)]: is the interpolation matrix;
{T(t)} is the vector of nodal temperatures.
We start by building the variation form of the Equation (1). We carry out a spatial discretization which consists in calculating the elementary integrals by using finite element and a temporal discretization.
There are many softwares that can implement the method of solving finite element problems in a more or less simple and convivial way. They are interested, especially in the grid of the object studied, automatic numbering of elements and nodes, the calculation of a solution, then the results map.
In this study, we use a commercial software “Comsol” based on the finite element method and which makes it possible to calculate the temperature evolution at any moment and in any point of material [22]. The material is considered isotropic. To investigate the influence of the thermal excitation on concrete test specimen, the following boundary conditions were applied to the model [23]:
1) A thermal heat impulse is simulated, which hits the surface of the test specimen with a heat flux of 1250 w/m2, a heating time t = 900 s, and a total simulation time of 4500 s.
2) The bottom side is supposed maintained to a constant temperature T0 = 20˚C, the other sides are supposed to be thermally insulated.
5.1. Influence of Concrete Cover
The concrete cover of defect is one of the parameters that should be determined with impulse thermography measurements. To analyze the influence of this parameter, the simulation is carried out with concrete cover from 0.05 m to 0.15 m, for a rust defect having thickness er, er = 2ep = 5.8 mm (see Figure 2).
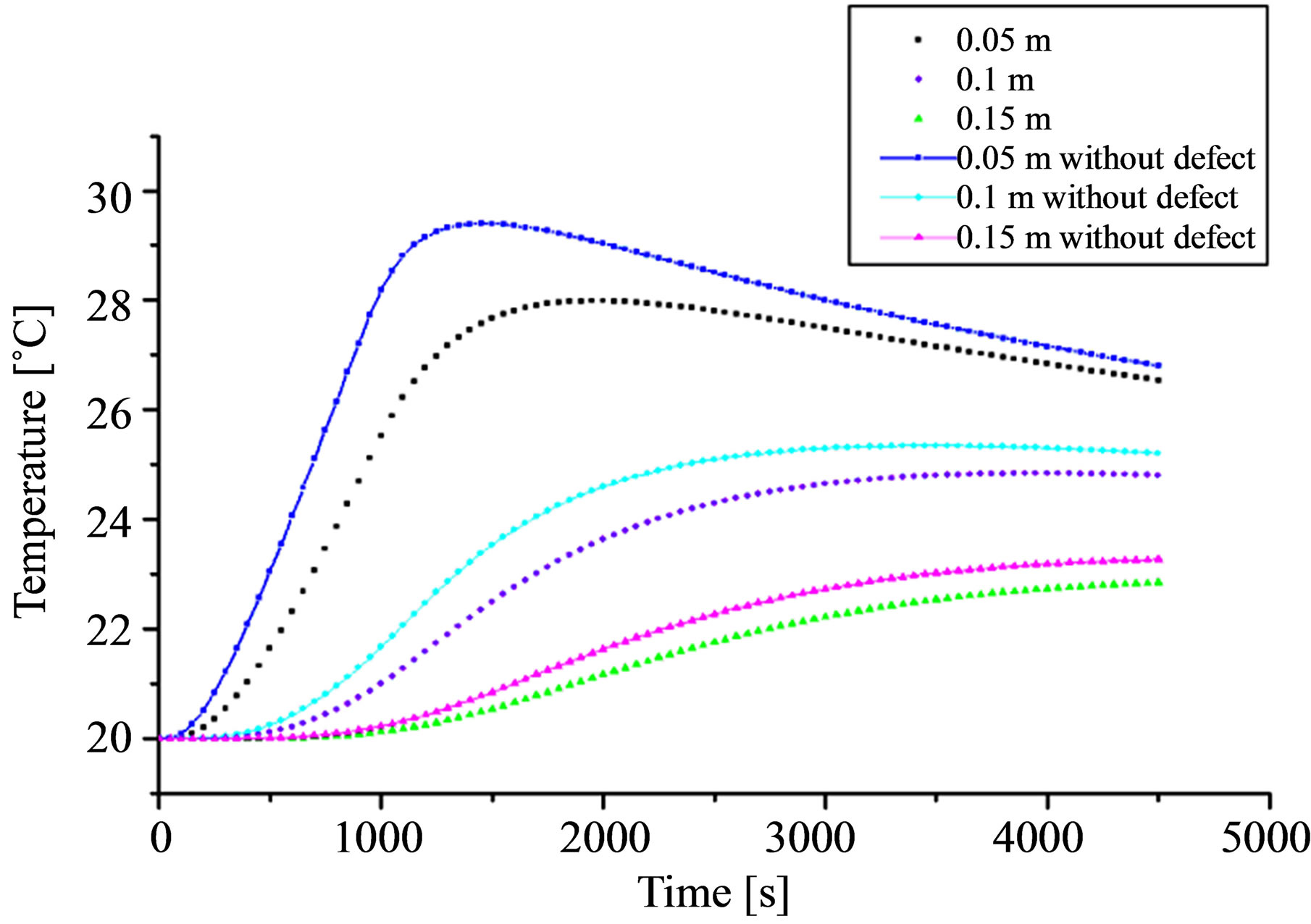
The thermographical images show the effect of the defect proximity to the input surface of the studied structure. The thermograms taken after 10 min, 30 and 60 min of cooling time (Figure 3) show only the temperature contrast of defect near the surface located at 0.05 m from the entry face. The temperature difference for 10 min is 1.2˚C, for 30 min is about 0.9˚C and 0.5˚C for 60 min of cooling time, so we can note that the suitable time to take thermograms is about 10 min of cooling time. Then, over time the effect of others defects appears gradually. This is related to the required time for heat to achieve the defect and detect it through the change in the thermophysical characteristics in the medium and translate this information at the input surface by a temperature contrast in the thermal image.
The curves of temperature versus time, Figure 4(a), show that for the three conduits; the presence of rust in conduits is translated by a drop of temperature compared to the same situation without rust. The temperature decreases when rising concrete cover. The value of the drop depends on the position of the rust in the specimen.
Figure 4(b) represents the spatial evolution of the transient surface temperature along the axis AB and re-
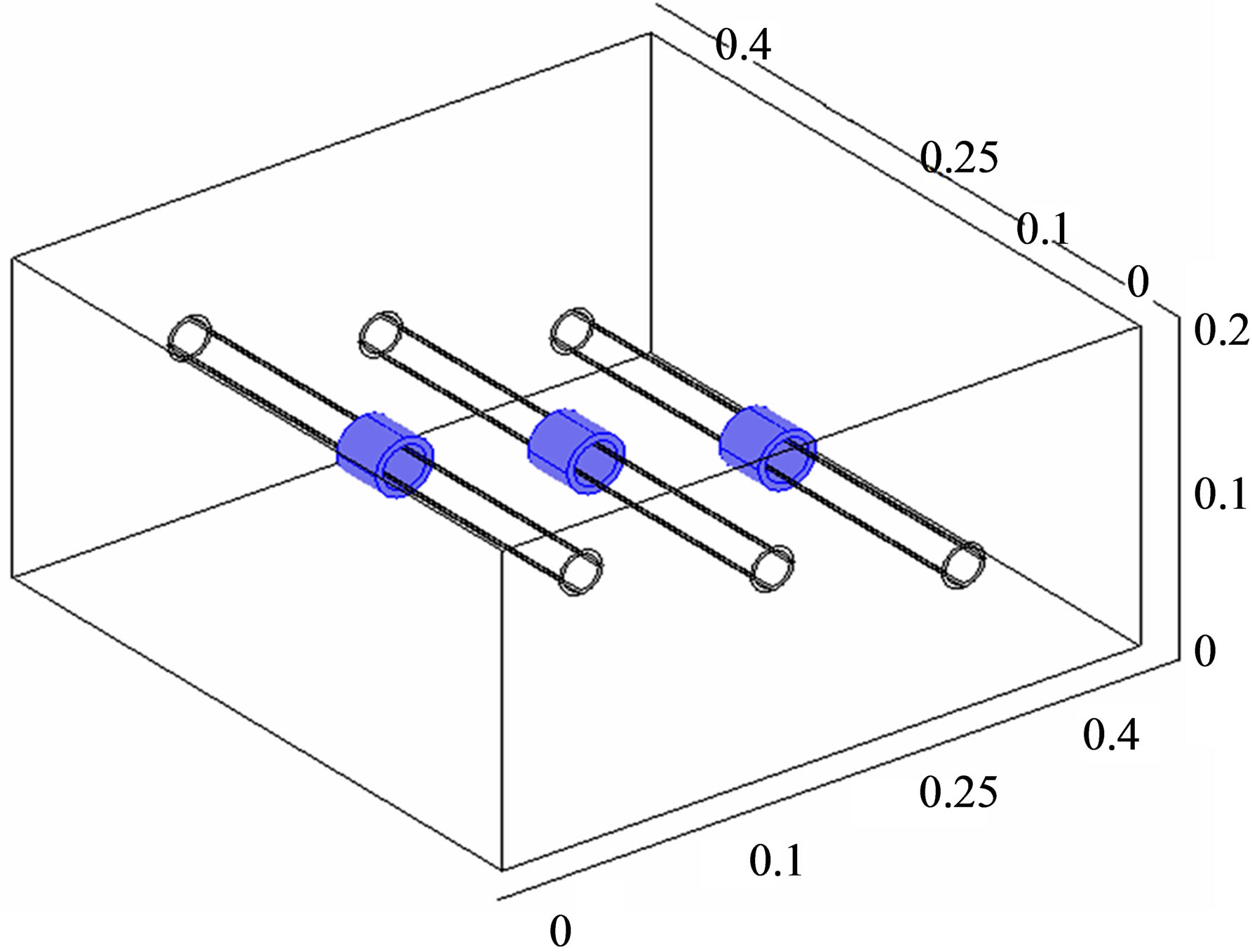
Figure 2. Adopted numerical model. The same defect placed at different positions in the concrete structure.
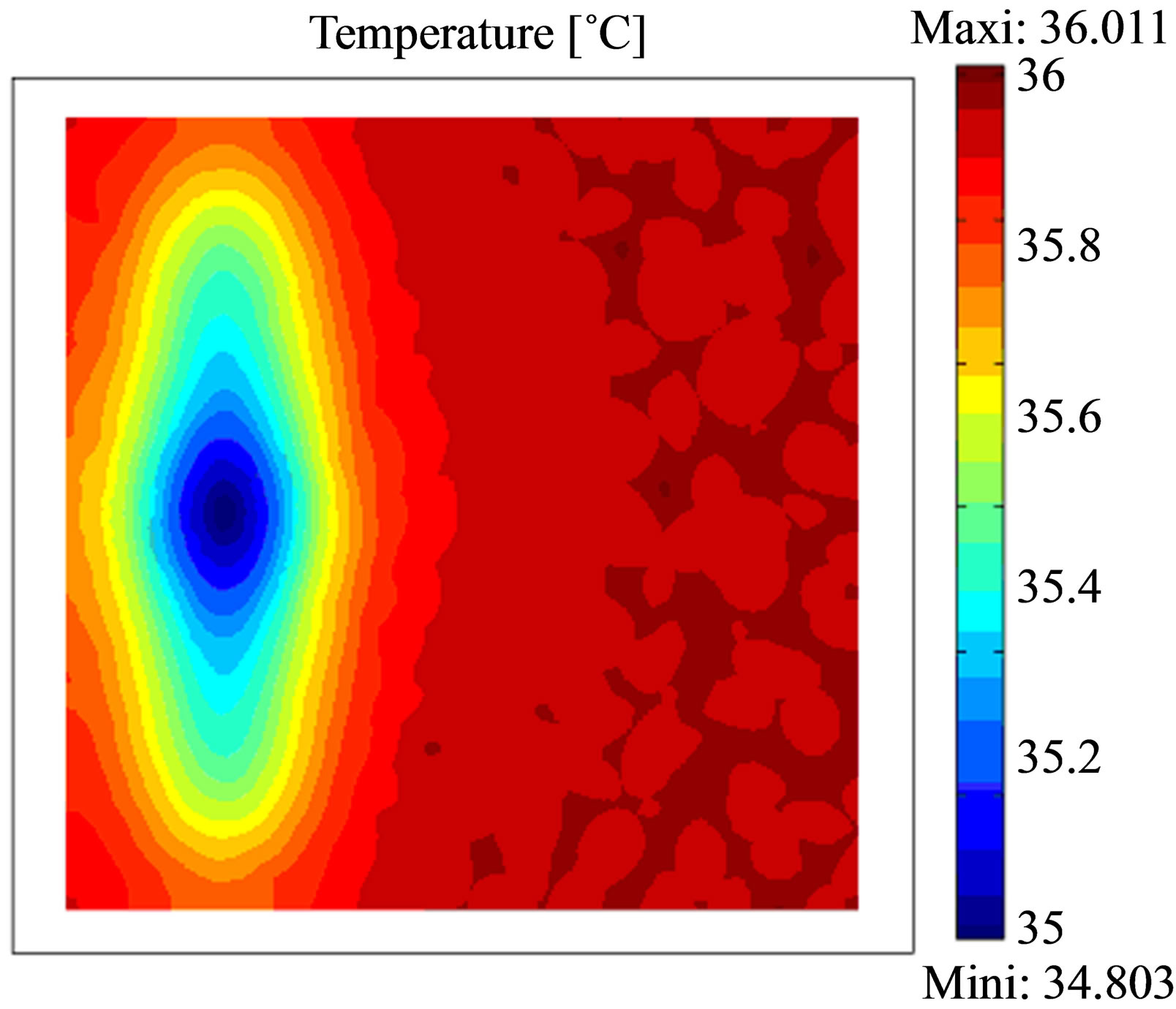
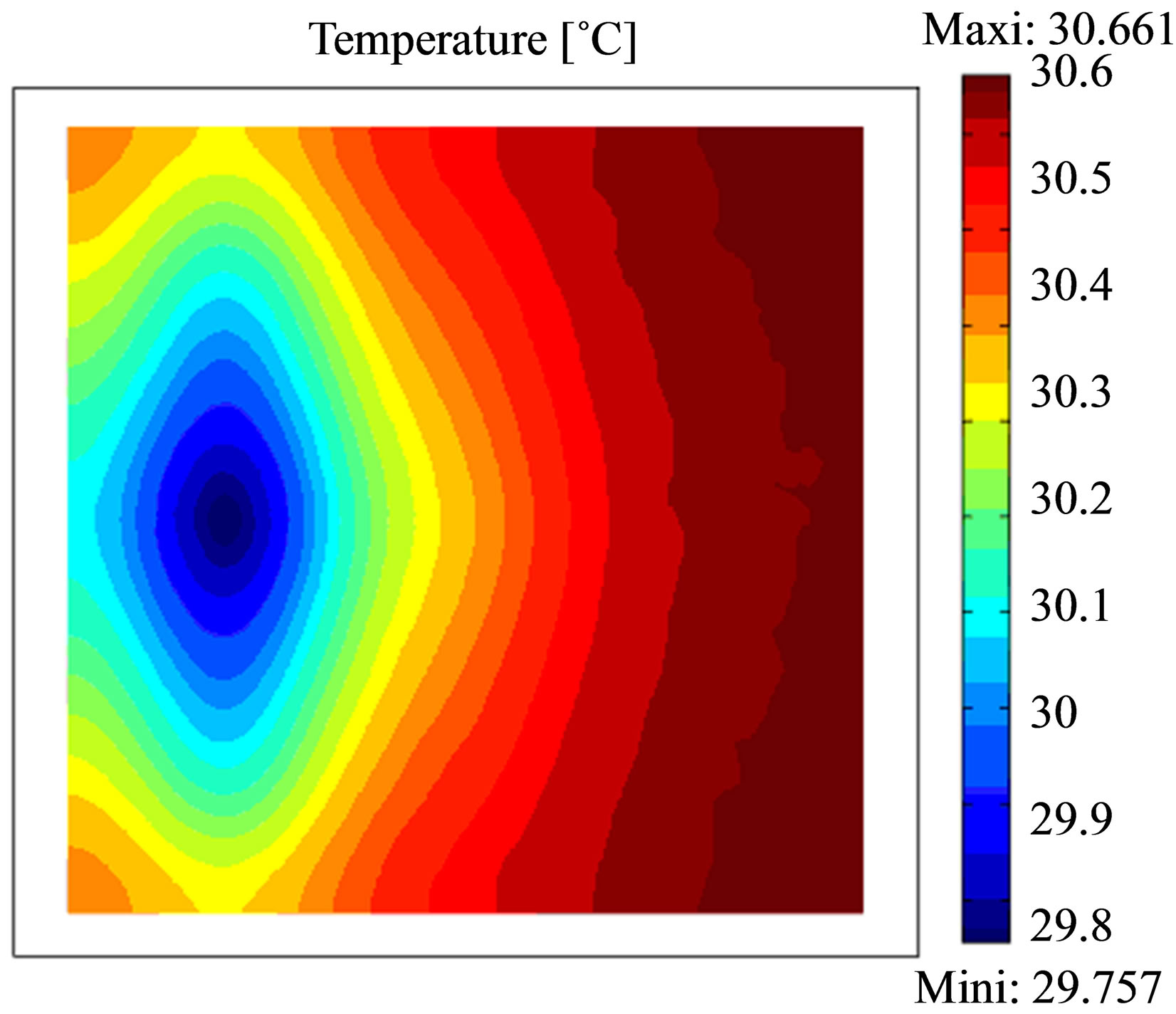
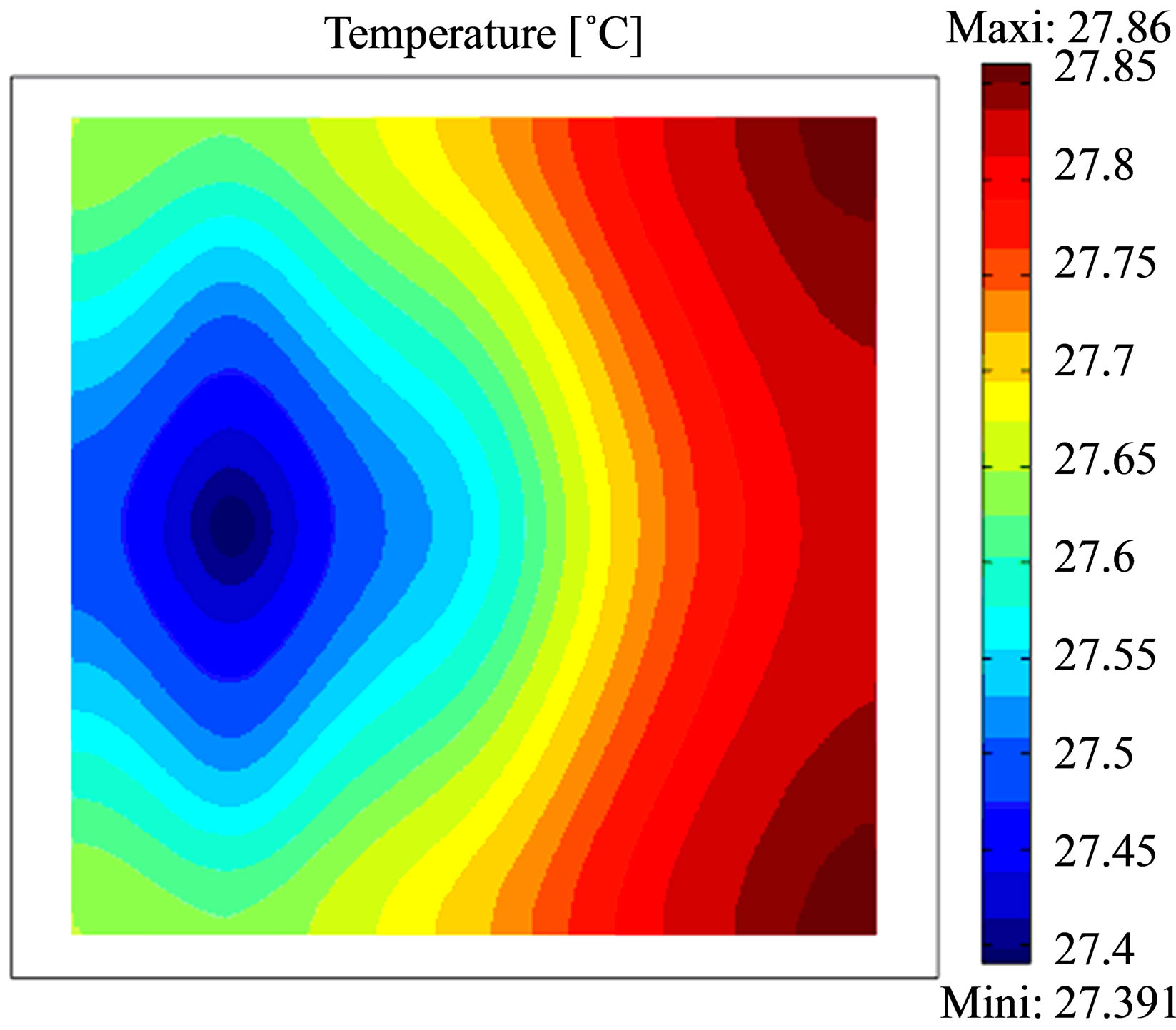
Figure 3. Thermograms recorded after a heating time of 15 min at the concrete specimen; top: cooling time 10 min; middle: cooling time 30 min and bottom: cooling time 60 min. Each thermogram was scaled to minimum and maximum.
corded after a cooling time of 10 min. During this time, there is only the effect of the rust that is closest to the surface of the specimen and that deeper rust layer does not appear well, due to the low temperature contrast, in fact the shallow pipe has good contrast after short cooling time which means that their detectability is greatly
 (a)
(a)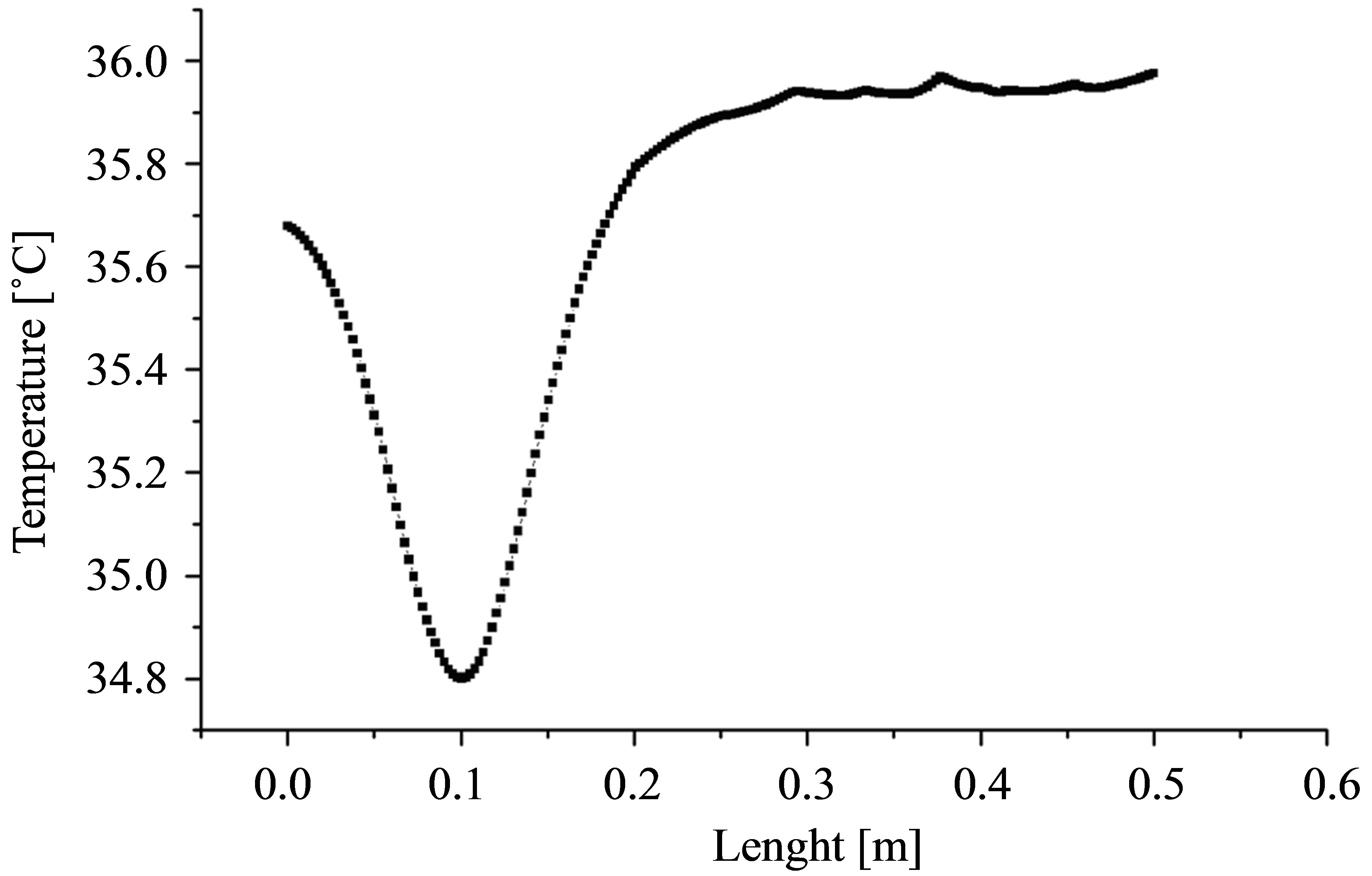 (b)
(b)
Figure 4. (a) Temperature evolution as a function of time calculated for a point taken on the center of rust surface on the three pipes and for a heating time of 15 mn. (b) Spatial evolution of surface temperature along the axis AB recorded after a cooling time of 10 min.
connected to the concrete cover.
This means that the information of the existence of the two others rusted areas has not yet the time to manifest on the surface by a temperature change. These investigations demonstrate that only the pipe in concrete up to a depth of 10 cm can appear, for those located at 15 cm it was not possible to detect them.
In order to analyze these results we represent, Figure 5, the temperature difference:
T (without rust)—T (with rust). The curves show that, to each position of the defect in the structure corresponds a minimum of this difference. When the rusted area is close to the entry surface the corresponding minimum is clear and the moment (abscissa) when it occurs is more accurate. This can give information, more accurate, on the rust position. When the rusted area is away from the input surface, the minima flattens and information on its position becomes less accurate.
5.2. Influence of Rust Size
Beside concrete cover, the rust size is another parameter affecting the thermal behaviour of rust. In this case of study, we take three different rust size, er = ep = 2.9 mm, er = 2ep = 5.8 mm and er = 4ep = 11.6 mm. For all of them the length of rust layer is 0.04 m (see Figure 6).
In the second configuration the three conduits are located at the same position by report to the sample surface, but the rust size is different from a pipe to the other.
The thermograms given in Figure 7 show that only the rust layer of a thickness er = 4ep appears with accuracy for a cooling time of 10 minutes, the other layer having the smallest thickness er = ep and er = 2ep appear when the cooling time increases. Nevertheless the temperature difference for 10 min is approximately 1.8˚C, 1.1˚C for 30 min and 0.5˚C for 60 min which means that’s the best time to take thermogram is between 10 and 30 min of cooling down.
In transient mode, the effect on the surface temperature that appears first is the region in which the thickness of the rust is the largest, task on the right in the three images. Versus time, is the effect of the average size of rust that appears and finally the smallest size.
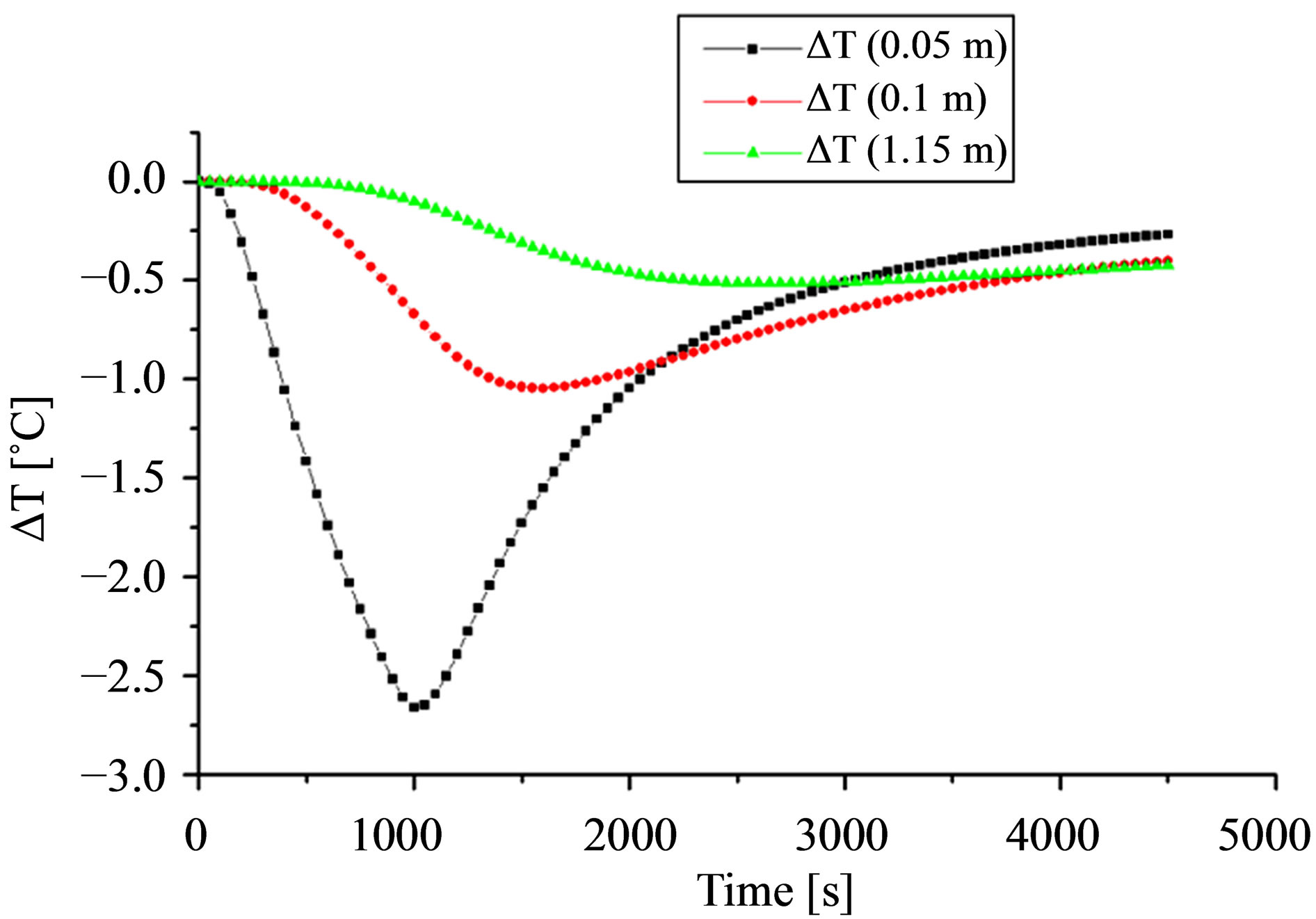
Figure 5. Temperature difference as a function of time calculated for a point taken on the center of rust surface on the three pipes.
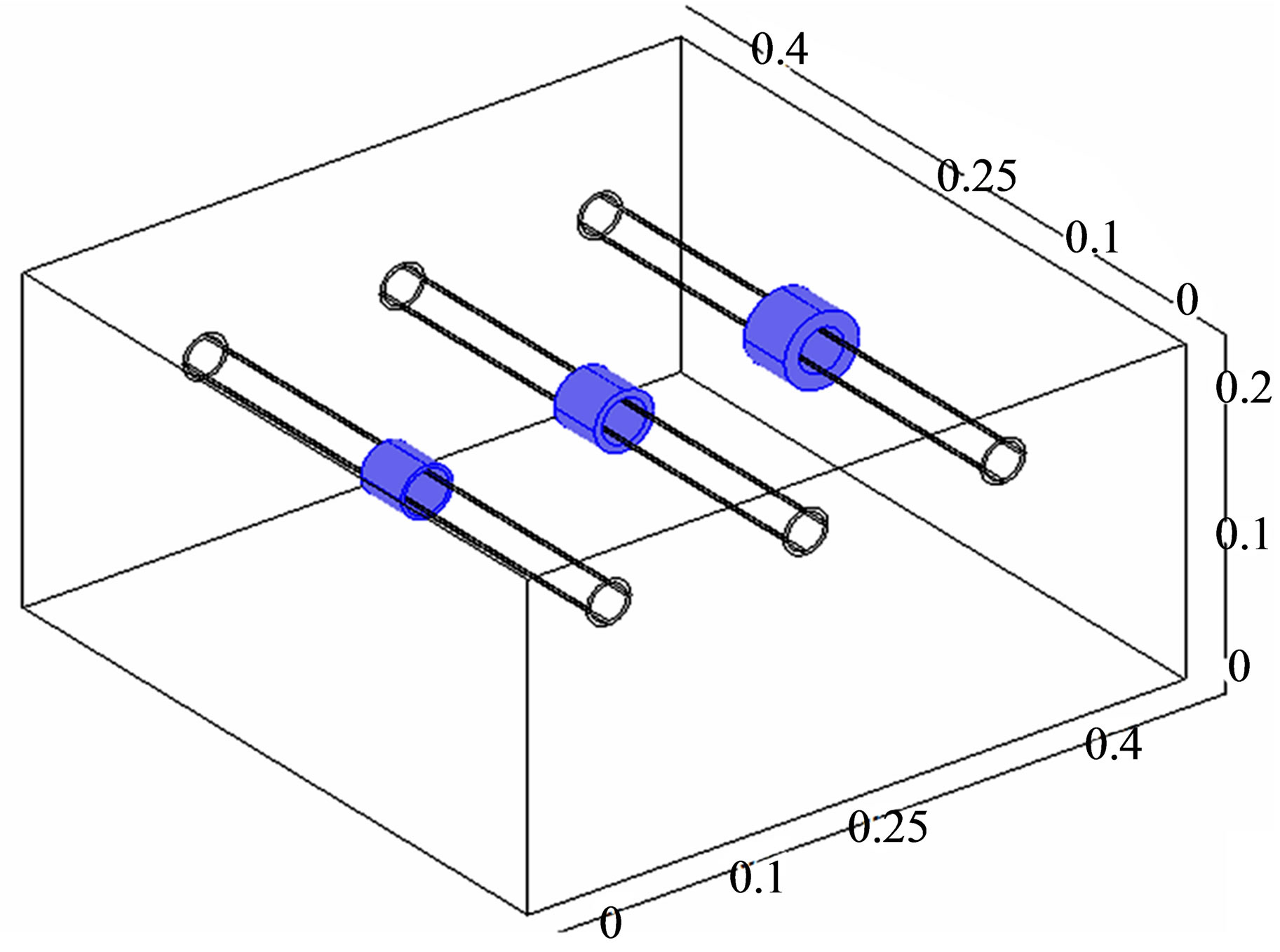
Figure 6. Adopted numerical model.
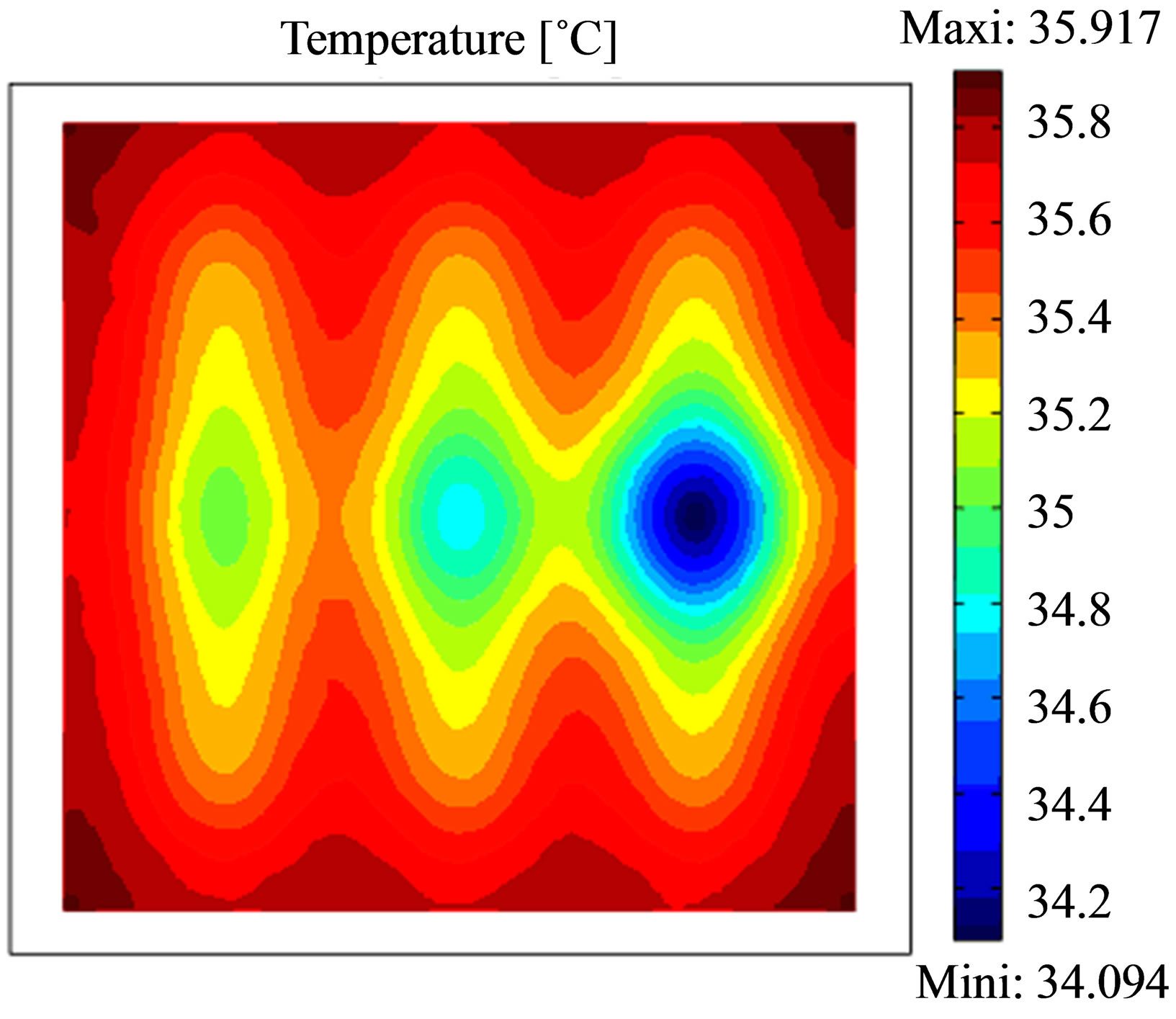
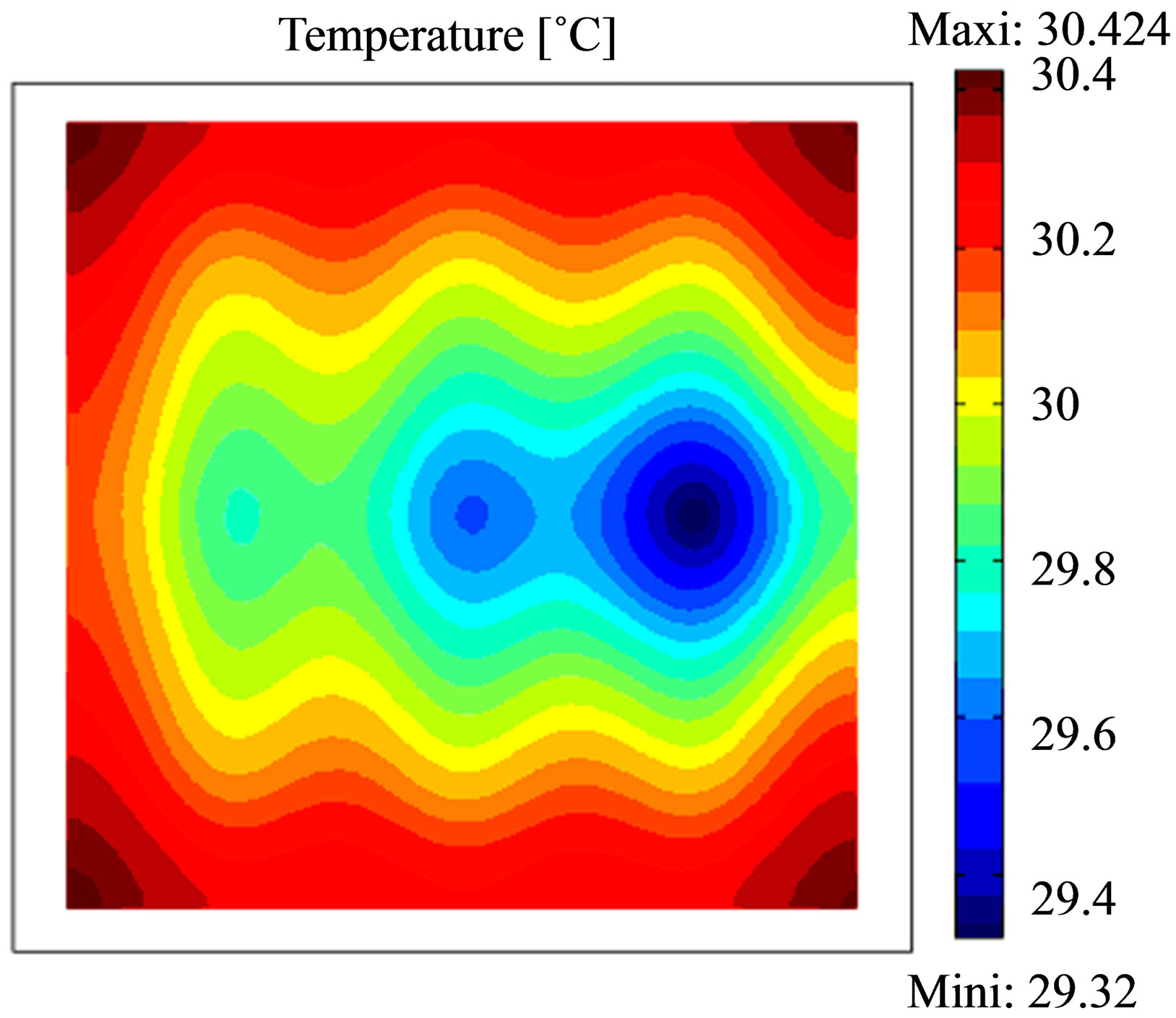
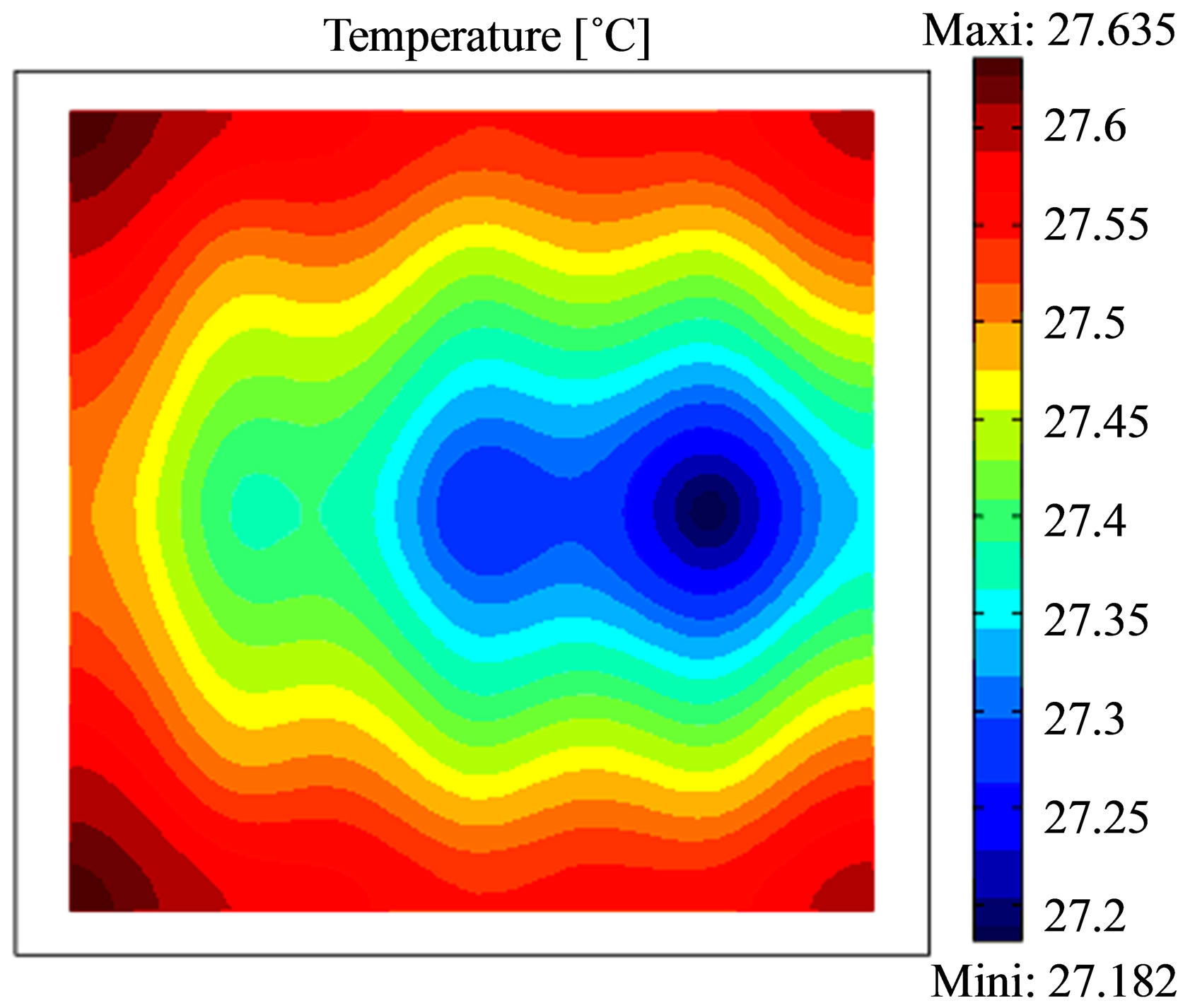
Figure 7. Thermograms recorded after a heating time of 15 min at the concrete specimen; Top: cooling time 10 min; middle: cooling time 30 min and bottom: cooling time 60 min. Each thermograms was scaled to minimum and maximum.
From these results, it appears that in transient mode, it is possible to detect the presence of different defects in the structure. Thermographical tasks, on the images, indicative of the presence of the defects are less wide in transient mode and may help to better locate them.
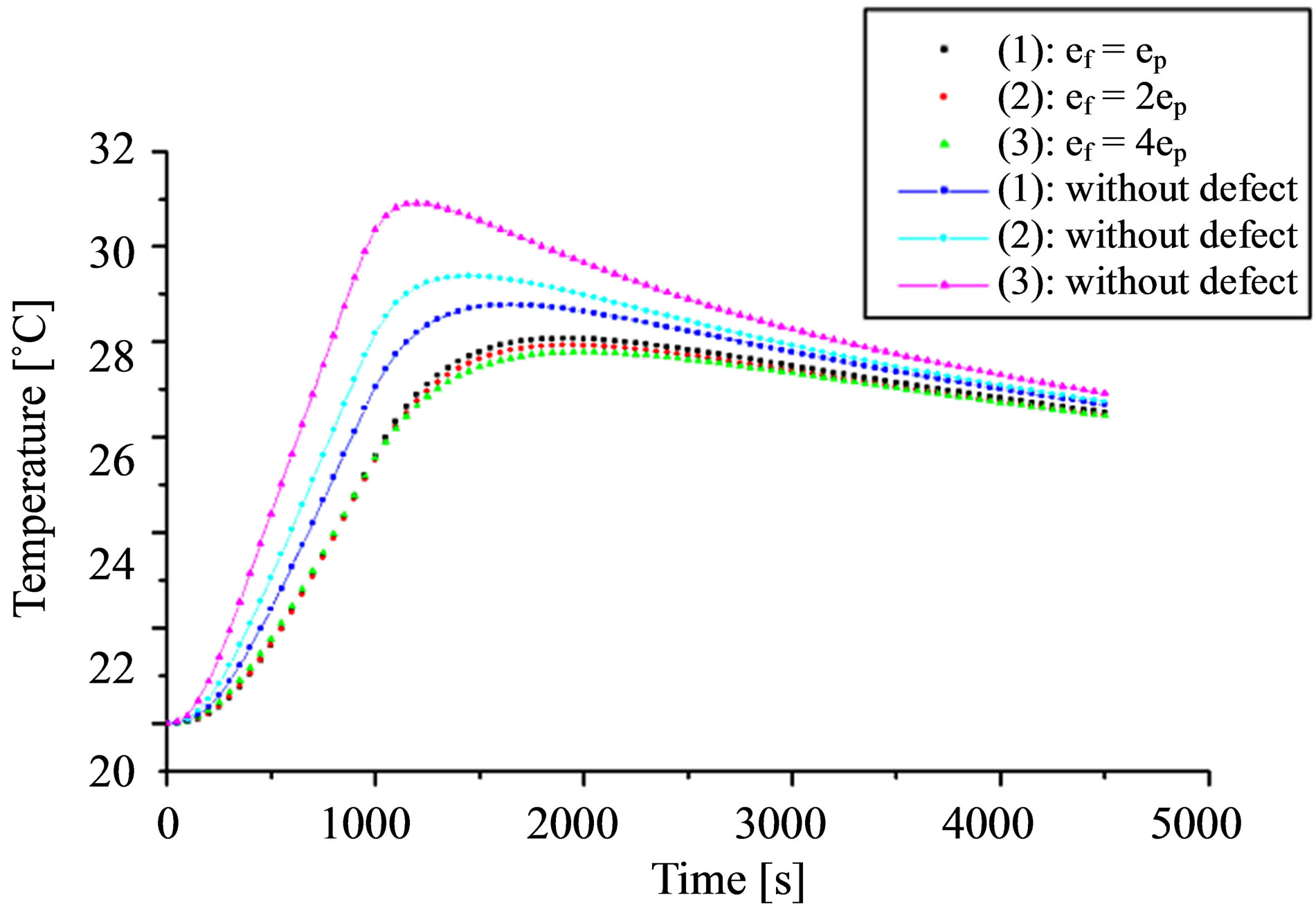
Figure 8(a) illustrates the temperature evolution ver-
 (a)
(a)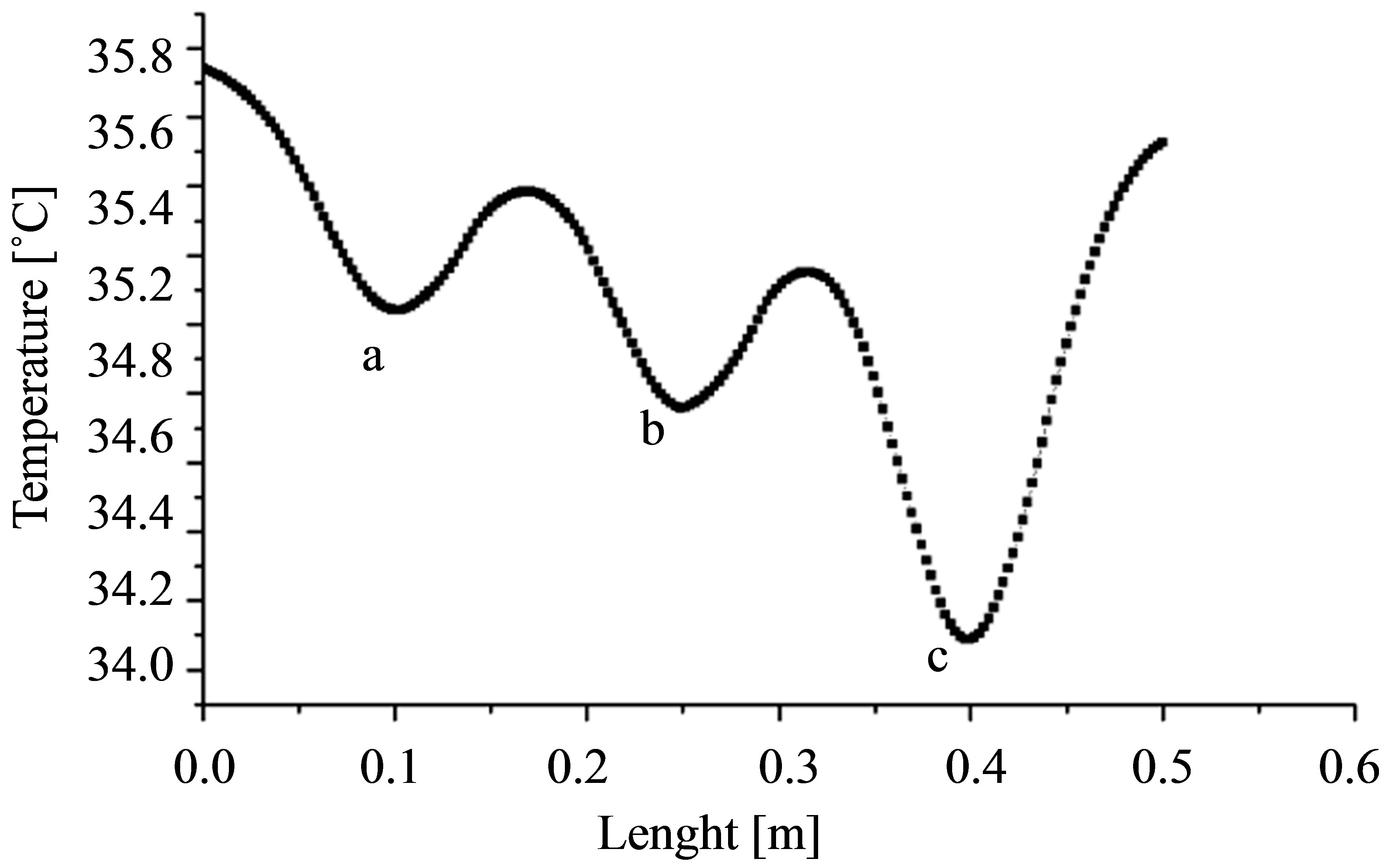 (b)
(b)
Figure 8. (a) Temperature evolution as a function of time calculated for the three points of rust a, b and c located at 0.1, 0.25 and 0.4, and heating time of 15 mn. (b) Spatial evolution of surface temperature along the axis AB recorded after a cooling time of 10 min.
sus time for a 15 minutes cooling, at points located in the center of each pipe rust. In the region without rust, curves are very close to each other, because of the small difference in their position by report to the surface input of specimen. In the presence of rust, there are different temperatures that depend on the size of the rusted area. Also, we can observe in Figure 8(b) the same phenomenon than before, but this time at the surface of the specimen. The minimas of curves are related to the positions of the rusted areas and their amplitudes are informative on the size of the rust, the maximum temperature difference occurs for the rust layer located at 0.4 m from the center of specimen (c) which accord with the rust layer having a thickness of er = 4ep. From these remarks, once can notice that the bigger the rust size the better is the temperature contrast which explains why the maximum temperature occurs for the larger thickness of rust layers.
We have also calculated the temperature difference T (without rust)—T (with rust) in Figure 9, in this second configuration. The curves show that the minimum abscissa is informative on the defect position and the am-
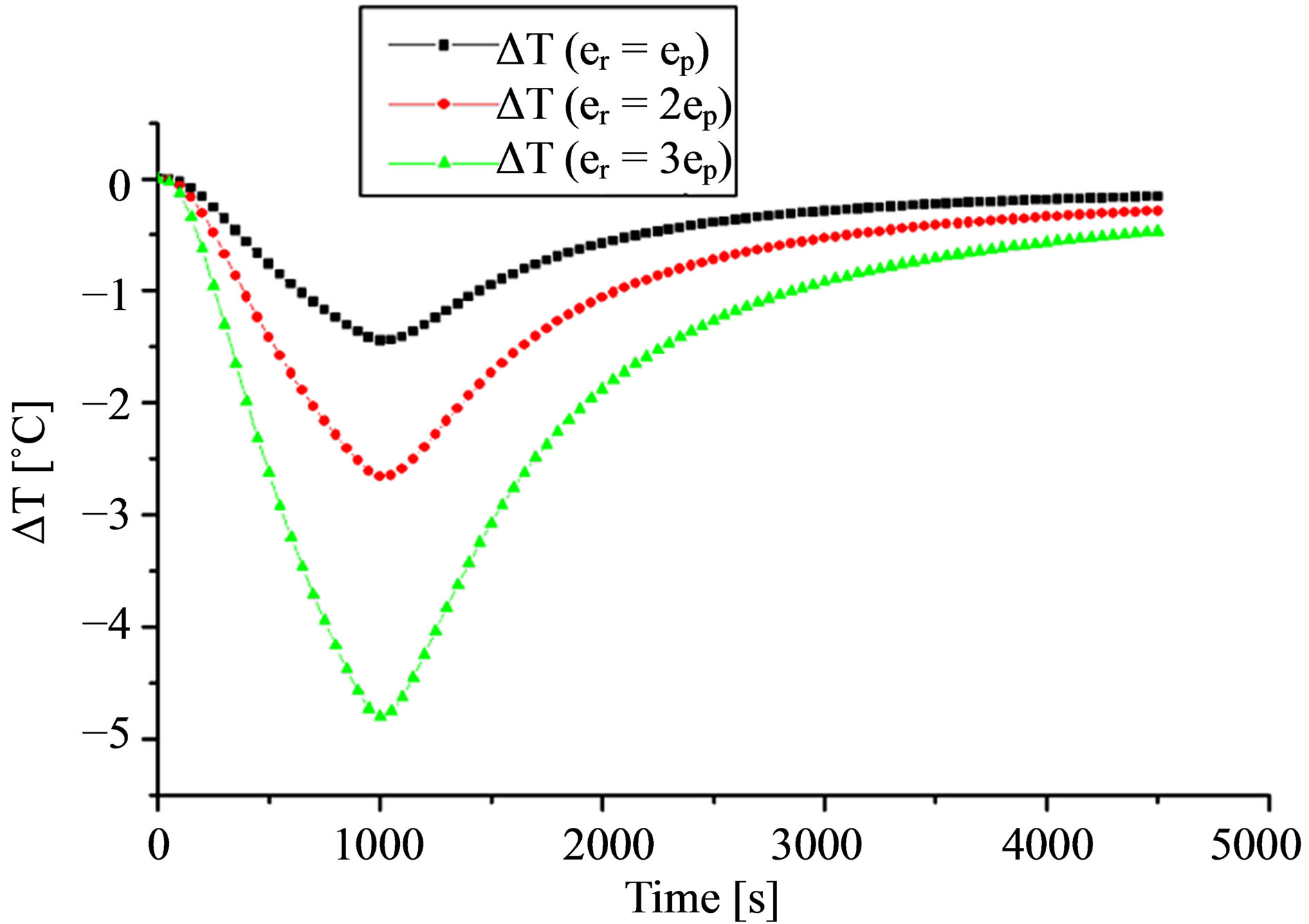
Figure 9. Temperature difference as a function of time calculated for a point taken on the center of rust surface on the three pipes.
plitude of this minima is informative on the size of the rusted area.
6. Conclusions
The investigations described before (qualitative data analysis and quantitative analysis) show that the analysis of warming up and cooling down process during and after heating with an external heat flux is a good tool to study the defects of behavior in concrete especially rust defect.
The numerical simulation can successfully help on the calibration of adequate time to take the thermal images. In fact numerical methods can be used to evaluate and validate the experimental results. The coupling of simulation and experiments can be of a great utility because it allows predicting the results before beginning the experiments. It helps to choose the suitable time to measure in optimal conditions. In this paper we have studied the numerical simulation forasmuch the cost and the duration of experiment can take more months or years in the case of artificially accelerated corrosion.
REFERENCES
- Y. Zhao, J. Yu, Y. Wu and W. Jin, “Critical Thickness of Rust Layer at Inner and Out Surface Cracking of Concrete Cover in Reinforced Concrete Structures,” Corrosion Science, Vol. 59, 2012, pp. 316-323. http://dx.doi.org/10.1016/j.corsci.2012.03.018
- F. J. Molina, C. Alonso and C. Andrade, “Cover Cracking as a Function of Rebar Corrosion: Part 2 Numerical model,” Materials and Structures, Vol. 26, No. 9, 1993, pp. 532-548. http://dx.doi.org/10.1007/BF02472864
- K. Bhargavaa, A. K. Ghoshb, Y. Moric and S. Ramanujama, “Model for Cover Cracking Due to Rebar Corrosion in RC Structures,” Engineering Structures, Vol. 28, No. 8, 2006, pp. 1093-1109. http://dx.doi.org/10.1016/j.engstruct.2005.11.014
- S. Marinetti and V. Vavilov, “IR Thermographic Detection and Characterization of Hidden Corrosion in Metals: General Analysis,” Corrosion Science, Vol. 52, No. 3, 2010, pp. 865-872. http://dx.doi.org/10.1016/j.corsci.2009.11.005
- M. Weiser, M. Rollig, R. Arndt and B. Erdmann, “Development and Test of a Numerical Model for Pulse Thermography in Civil Engineering,” Heat Mass Transfer, Vol. 46, No. 11-12, 2010, pp. 1419-1428. http://dx.doi.org/10.1007/s00231-010-0656-9
- M. R. Clark, D. M. McCann and M. C. Forde, “Application of Infrared Thermography to the Non-Destructive Testing of Concrete and Masonry Bridges,” NDT&E International, Vol. 36, No. 4, 2003, pp. 265-275. http://dx.doi.org/10.1016/S0963-8695(02)00060-9
- T. Sakagami and S. Kubo, “Development of a New Non-Destructive Testing Technique for Quantitative Evaluations of Delamination Defects in Concrete Structures Based on Phase Delay Measurement Using Lock-In Thermography,” Infrared Physics & Technology, Vol. 43, No. 3-5, 2002, pp. 311-316. http://dx.doi.org/10.1016/S1350-4495(02)00157-3
- H. Wiggenhauser, “Active IR-Applications in Civil Engineering,” Infrared Physics & Technology, Vol. 43, No. 3-5, 2002, pp. 233-238. http://dx.doi.org/10.1016/S1350-4495(02)00145-7
- N. Laaidi and S. Belattar, “Application of Thermal Non Destructive Testing Method to Oil Conduits Control,” 5th Pan American Conference for NDT, Cancun, 2-6 October 2011.
- N. Laaidi and S. Belattar, “Modeling of Damages in the Bridges,” The 10th International Conference of the Slovenian Society for Non-Destructive Testing “Application of Contemporary Non-Destructive Testing in Engineering”, 1-3 September 2009, Ljubljana, 2009, pp. 149-158.
- N. Laaidi and S. Belattar, “The Numerical Modeling and the Infrared Thermography Principle Applied to the Analysis of Corrosion Defects in Oil Conduits,” QIRT 2012, ID-114.
- N. Laaidi and S. Belattar, “Damages in the Bridges. Modeling and Analysis of Defects of Cracks and Corrosion Type,” Simulation in NDT, Online Workshop, 2010. www.ndt.net
- Y. Yuang, Y. Ji and J. Jiang, “Effect of Corrosion Layer of Steel Bar in Concrete on Time-Variant Corrosion Rate,” Materials and Structures, Vol. 42, No. 10, 2009, pp. 1443-1450. http://dx.doi.org/10.1617/s11527-008-9464-9
- Ch. Maierhofer, R. Arndt, M. Rollig, C. Rieck, A. Walther, H. Scheel and B. Hillemeier, “Application of Impulse-Thermography for Non-Destructive Assessment of Concrete Structures,” Cement & Concrete Composites, Vol. 28, No. 4, 2006, pp. 393-401. http://dx.doi.org/10.1016/j.cemconcomp.2006.02.011
- CH. Cheng, T. Ming Cheng and C. H. Hung Chiang, “Defect Detection of Concrete Structures Using Both Infrared Thermography and Elastic Waves,” Automation in Construction, Vol. 18, No. 1, 2008, pp. 87-92. http://dx.doi.org/10.1016/j.autcon.2008.05.004
- M. Dekoster, O. Blanpain, F. Buyle-Bodin and O. Maurel, “Etude de l’Evolution des Coefficients de Sécurité des Ouvrages en Béton Armé Dégradé selon Différents Scénarios de Corrosion,” XXIIiemes Rencontres Universitaires de Génie Civil, Ville & Genie Civil, 2004.
- Q. T Nguyen, S. Caré, Y. Berthaud and A. Millard, “Analyse de la Fissuration du Béton Armé en Corrosion Accélérée,” Comptes Rendus Mécanique, Vol. 335, No. 2, 2007, pp. 99-104. http://dx.doi.org/10.1016/j.crme.2007.01.005
- E. Grinzato, V. Vavilov and T. Kauppinen, “Quantitative Infrared Thermography in Buildings,” Energy and Buildings, Vol. 29, No. 1, 1998, pp. l-9. http://dx.doi.org/10.1016/S0378-7788(97)00039-X
- Y. He, G. Tian, L. Cheng, H. Zhang and P. Jackson, “Parameters Influence in Steel Corrosion Evaluation Using PEC Thermography,” Proceedings of the 17th International Conference on Automation & Computing, Huddersfield, 10 September 2011.
- A. Elballouti and S. Belattar, “Thermal Non-Destructive Characterisation of Layers Detachment in the Roadways,” Int. J. of Materials and Product Technology, 2011, 4117- 26.
- N. Laaidi, S. Belattar and A. Elballouti, “Pipeline Corrosion, Modeling and Analysis,” Journal of Nondestructive Evaluation, Vol. 30, No. 3, 2011, pp. 158-163. http://dx.doi.org/10.1007/s10921-011-0103-y
- W. B. J. Zimmerman, “Process Modelling and Simulation with Finite Element Methods, World Scientific Series on Stability, Vibration and Control of Systems,” Series A. Singapore, 2004.
- C. H. Maierhofer, A. Brink, M. Rollig and H. Wiggenhausser, “Quantitative Impulsethermography as Non-Destructive Testing Method in Civil Engineering—Experimental Results and Numerical Simulations,” Construction and Building Materials, Vol. 19, No. 10, 2005, pp. 731- 737. http://dx.doi.org/10.1016/j.conbuildmat.2005.06.002

