Received 1 September 2015; accepted 24 October 2015; published 27 October 2015

ABSTRACT

Aerosols are the tiny suspended particles in the atmosphere playing a major role in influencing the net radiation budget of the earth. The aerosols also affect cloud microphysics and those with land origin, possibly reduce the monsoon rainfall. Dynamic and diverse nature of the aerosols varies according to different locations. The aerosols originating due to desert dust, rural atmospheric situations, urban pollutants and marine areas have wide variations and display specific characteristics. Routine monitoring of aerosol events and their subsequent dispersal pattern are important in order to understand their role in climatic process. Hence, it is very important to study the aerosols and their retrieval strategy from the ocean colour remote sensing sensors. The satellite sensors provide platform for making observations covering large area as also their short- term and frequent repetivity. Ocean-colour sensors e.g. CZCS, SeaWiFS, MODIS, POLDAR, Oceansat-1 & 2 OCM have been used to study aerosols, apart from being used to study ocean-colour. Most of the ocean-colour sensors are equipped with a few additional near infrared (NIR) bands (λ > 700 nm), which are helpful in providing vital information on atmospheric aerosols due to strong absorption by water in NIR wavelengths. The present work is an attempt to study the temporal and spatial variations of Aerosol Optical Depth (AOD) over the Bay of Bengal using Oceansat-2 Ocean Colour Monitor (OCM).

Keywords:

AOD, OCM-2, Atmospheric Correction

1. Introduction

Atmospheric aerosol plays a significant role in the Earth’s radiation budget through radiative forcing and chemical perturbations. The net effect of aerosols is to cool the climate system by reflecting sunlight [1] . Quantifying the net effect requires accurate information on the distribution of aerosol properties that have to be estimated from satellite observations. Estimating aerosol properties is also one of the first and important steps in generating high-level ocean colour products from satellite observations. The major problem in their characterization is on account of their short lifetime because of which they have high spatial and temporal variability [2] . The transport processes may bring in aerosols from other locations and affect the local climate there. These factors reinforce the necessity of aerosol monitoring on a larger spatial scale than can be provided by the ground based measurements (IPCC, 2001). Satellite based observations can provide detailed knowledge in this regard on a long timescale covering a large spatial area [3] . Aerosol monitoring from space based instruments consists in extracting the atmospheric contribution from the total signal measured by the satellite sensor. Aerosol monitoring from previous sensors was limited to studies over oceans which have a distinct advantage in that the total measured signal is not much affected by reflectance from ocean surface away from sun-glint area [4] . Aerosol retrieval over oceans is thus more accurate and reliable.

Aerosol particles are important to scientists because they represent an area of great uncertainty in their efforts to understand the Earth’s climate system. Depending upon their size, type, and location, aerosols can either cool the surface, or warm it. They can help clouds to form, or they can inhibit cloud formation. And if inhaled, aerosols can be harmful to people’s health. There are many applications for aerosol optical thickness data: 1) atmospheric correction of remotely sensed surface features; 2) monitoring of sources and sinks of aerosols; 3) monitoring of volcanic eruptions and forest fire; 4) radiative transfer model; 5) air quality; 6) health and environment; 7) earth radiation budget; 8) climate change [5] .

2. OCM-2 Instrument

OCM-2 sensor is the follow on sensor of OCM-1 and is designed to measure the spectral variability of the water leaving radiance that is related to the concentration of phytoplankton pigments, suspended matter and coloured dissolved organic matter in coastal and ocean waters, and to characterize the atmospheric aerosols. Oceansat-2, OCM (OCM-2) is identical to OCM-1, except minor spectral shift in band 6 and 7. In OCM-1, band-6 centered at 670 nm is shifted to 620-nm in OCM-2 for better quantification of suspended sediments and band 7 centered at 765-nm is shifted to 740-nm to avoid oxygen absorption as shown in Figure 1. The technical details and algorithms developed for retrieving the geophysical data products from OCM-2 can be obtained from [6] . The coverage for LAC and GAC is shown in Figure 2. The technical specifications of OCM-1 and OCM-2 are presented in Table 1.

3. Geophysical Parameters from OCM-2 Data

The geophysical products from Oceansat-II OCM data at basic spatial resolution of 360 meters along with their specifications are shown in the Table 2. The normalized water-leaving radiance in 412, 443, 490, 510 and

555-nm bands will be the output of the atmospheric correction procedure and will be subsequently used in the estimation of bio-geo-physical variables. The chlorophyll-α product can be used as a proxy to the presence of phytoplankton in the seawater as chlorophyll-α is the dominant pigment found in most of the phytoplankton. The diffuse attenuation coefficient (K_d) product is an apparent optical property, which defines the rate of decrease of downwelling irradiance falling with depth in the water column. The total suspended matter (TSM) product will provide quantitative measure of the inorganic particulate matter present in the suspended form mainly in the coastal waters. The aerosol optical depth (AOD) is a measure of the atmospheric turbidity, which will be characterized at 865-nm, as this wavelength is almost insensitive to reflectance from ocean waters.

4. Retrieval Strategy

The geophysical retrieval procedures will be applied only to cloud free water pixels for daytime conditions over open-ocean and coastal waters that are not affected by sun glint. If a cloud mask, land mask or sun glint mask is not set for a given pixel geophysical retrieval for OCM-2 top-of-atmosphere (TOA) radiances is performed. To perform atmospheric correction, non-OCM-2 data sets such as total ozone amount and sea surface wind will also be required. The output of the atmospheric correction algorithm will be water-leaving reflectance or remote sensing reflectance (R_rs), which will form input to the in-water bio-optical algorithms. The atmospheric correction algorithm over shallow water or turbid water will be performed by “borrowing” the aerosol properties over the nearest deep water.

5. Cloud Masking

Seawater, and its constituents alter spectral composition of visible (400 - 700 nm) radiation reaching the satellite sensor. However, near infrared (NIR) radiation is strongly absorbed by relatively clear water, resulting in a uniformly low albedo. Clouds, in contrast, have a wide range of reflectivity at the wavelength measured by OCM sensor. An albedo-based cloud masking approach has been adopted for OCM processing by making uses of NIR band centred at 865 nm. The albedo at 865-nm, α₈₆₅ is calculated using the following equations:

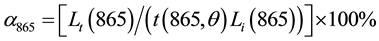(1)

where, L_t(865) is the total radiance at the sensor at 865-nm, L_i(865) is the incident light at 865-nm, t(865, λ) is the diffuse transmittance between the surface and sensor at 865-nm, and θ is the satellite zenith angle [7] . The diffuse transmittance between the surface and sensor at 865 nm is calculated as

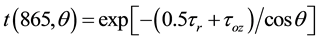(2)

where τ_r, τ_oz are the Rayleigh and ozone optical thicknesses respectively, at 865-nm. The incident light at 865-nm is computed as

(3)

where F₀ is the extra-terrestrial solar irradiance at 865-nm and θ₀ is the solar zenith angle. The diffuse transmittance between the sun and the ocean surface at 865-nm follows from Equation (2), is calculated as;

(4)

It was found that OCM image pixels of 865-nm band having albedo greater than 1.1% would be masked successfully for clouds/thin clouds and haze. This threshold value is also found to be effective for masking land and sun glint affected pixels as well.

6. Sun Glint Mask and Correction

Sun glint refers to the phenomenon of incoming solar radiation directly reflected from the ocean surface to the sensor. For an absolutely flat ocean surface, the sun glint occurs at one point where the zenith angles of sun and sensor are identical and their azimuth angles are opposite. However, the ocean surface is never absolutely flat. The wind-derived surface roughness enlarges the sun glint area. For remote sensing of the ocean and atmosphere optical properties, the measurement of radiances affected by sun glint has to be avoided and masked out. There are usually no meaningful retrievals in regions significantly contaminated by sun glint. The Oceansat-2 OCM is capable of operationally tilting the sensor ± 20˚ away from the nadir to minimize sun glint contamination. An operational scheme is developed and optimal tilt angles have been identified to minimize the sun-glint in different seasons for the Arabian Sea and Bay of Bengal for Oceansat-1 OCM data [8] . Apart from implementing this technique some OCM data showed sun-glint in the months of April and August. A method proposed by [9] to determine when sun glint needs to be masked out. The probability of a pixel being contaminated by sun glitter for the incoming sun direction (θ₀,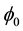) and the observing direction (θ,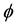) can be written as

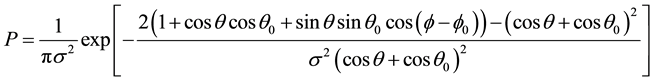(5)

where, σ² is the mean square surface slope [10] which is a function of wind speed, W_s

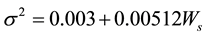(6)

A threshold value of 1.5 percent for the probability to mask out the sun glint area will be used.

7. Atmospheric Correction Algorithm Description

7.1. Processing Outline

The Ocean colour data processing for the retrieval of the geophysical parameters is a two-step procedure. The first procedure involves the atmospheric correction of the top of the atmosphere (TOA) sensor detected radiances to estimate the sea surface reflectivity. The output of this atmospheric correction procedure will be subsequently used for the estimation of in-water and atmospheric variables.

Figure 3 presents a schematic flowchart for the Gordon-Wang atmospheric correction algorithm, adapted from [11] and also subsequently used for OCM data processing by [12] . The total radiance L_t, measured at the top of the atmosphere in each of the visible to near-infrared bands is divided by the extraterrestrial solar irradiance F₀ to obtain the measured reflectance, ρ_t. The extraterrestrial solar irradiance (F₀) values will be computed for the OCM spectral response functions (SRF). The reflectance contributed by whitecaps is estimated from the surface wind speed W and subtracted from ρ_t. Corrections for ozone absorption and Rayleigh reflectance ρ_r are applied to obtain the ρ_t − ρ_r term, which is considered equivalent to aerosol reflectance in the two NIR bands of OCM-2 data i.e. 740-nm and 865-nm. The algorithm then calculates the spectral dependency of the candidate aerosol type based on the value of epsilon parameter, which is ratio of aerosol reflectance in the 740 and 865-nm bands, assuming that the water-leaving reflectance in each of these bands is zero due to strong absorption of light by water beyond 700-nm. Extrapolation of the aerosol reflectance in shorter wavelength for each pixel is done using an exponential model for aerosol spectral behavior with epsilon parameter as an exponent. After subtraction of the aerosol contribution, the water-leaving reflectance is obtained in each of the visible bands by dividing by the diffuse atmospheric transmittance.

7.2. Theoretical Description of the Atmospheric Correction Algorithm

The reflectance backscattered from the atmosphere and/or sea surface is typically at least an order of magnitude

larger than the desired radiance scattered out of the water. The contributions of the water-leaving reflectance to the TOA reflectance decreases with the increase of the viewing angle because of the reduction of the diffuse transmittance. Therefore, it is mandatory to correct for atmospheric effects, to retrieve any quantitative parameter from space. This section describes the basis of the algorithm for removing the atmospheric effects from the OCM-2 imagery over the ocean to derive normalised water-leaving radiance in the visible range of electromagnetic spectrum. The normalised water-leaving radiance, [L_w]_N, has been defined by [13] in a following manner,

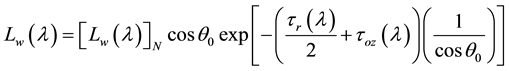(7)

where, L_w(λ) is the radiance backscattered out of the water at a wavelength λ, τ_r(λ) and τ_oz(λ) are the optical thickness of the atmosphere associated with molecular (Rayleigh) scattering and Ozone absorption, respectively and θ₀ is the solar zenith angle. The normalised water leaving radiance is approximately the radiance that would exit the ocean in the absence of the atmosphere with the sun at the zenith.

The radiance received by a ocean colour sensor at the top of the atmosphere (TOA) in a spectral band centred at wavelength λ, L_t(λ), can be divided into the following components: L_path(λ) the radiance generated along the optical path by scattering in the atmosphere and by specular reflection of the atmospherically scattered light from the sea surface; L_g(λ) the contribution arising from specular reflection from the sea surface (sun glitter), and, L_w(λ) the desired water-leaving radiance; i.e.,

(8)

Converting the Equation (8) in terms of reflectance, where, the reflectance ρ is defined as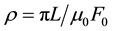, where L is the radiance in a given solar and viewing geometry, F₀ is extra-terrestrial solar irradiance, and μ₀ is the cosine of the solar zenith angle, the Equation (8) can be rewritten as

(9)

where, ρ_a and ρ_r are the reflectance generated along the optical path by scattering in the atmosphere due to aerosol and Rayleigh scattering, ρ_ra(λ) is a multiple interaction term between molecules and aerosols, ρ_g is the specular reflection or sun glitter component and ρ_w is the desired water leaving reflectance. In Equation (9), T and t are the direct and diffuse transmittance terms, respectively. The direct component of the transmittance T is associated with the sun glitter term, which is highly directional. The direct transmittance is given by

(10)

where μ_v is the satellite viewing angle and τ_r, τ_a, τ_oz are, the Rayleigh, aerosol, and Ozone optical thicknesses. The diffuse transmittance t, associated with water leaving reflectance term in Equation (9) is given by [14] as

(11)

The Rayleigh reflectance path radiance, ρ_r, is computed by the following equation,

(12)

where, ω_0r is single scattering albedo for molecular scattering, τ_r is the spectral Rayleigh optical depth, F₀ is extra-terrestrial solar flux, P_r is the molecular scattering phase function and m_v = cosq_v. The Rayleigh scattering phase function is given as [15]

(13)

The forward/backward scattering angle g^± in Equation (13) is computed as

(14)

where f is the relative azimuth (sensor azimuth―sun’s azimuth), θ_v is the sensor viewing angle and θ₀ is the sun zenith angle (illumination directions). The variability of the mean extraterrestrial solar flux, F₀, for seasonal variation of the Earth-Sun distance is calculated by following equation

(15)

where, d² is the factor accounting for the actual Sun-Earth distance as a function of the Julian day of the year and μ₀ is the cosine of the solar zenith angle. The optical depth τ_oz(λ) can be assumed constant over time and space around Indian region and nominal values of τ_oz for OCM bands 1 to 8 are 0, 0.00163, 0.0090, 0.0193, 0.0364, 0.0405, 0.0040, and 0, respectively.

The Single Scattering Approximation

In Equation (9), ρ_ra is the interaction term between molecular and aerosol scattering [16] . The term ρ_ra accounts for the interaction between Rayleigh and aerosol scattering, e.g., photons first scattered by the air then scattered by aerosols, or photons first scattered by aerosols then air, etc. This term is considered as zero in the single scattering case, in which photons are only scattered once, and it can be ignored as long as the amount of multiple scattering is small, i.e., at small Rayleigh and aerosol optical thicknesses and [17] has shown that it is useful to consider path radiance term in the limit that the optical thickness of the atmosphere is =1. This is referred as the single-scattering limit. Formulas for the reflectance in this limit are referred as the single-scattering approximation. For a single scattering approximation Equation (9) can be rewritten as

(16)

where, aerosol contribution ρ_as is provided by:

(17)

where is the aerosol scattering phase function for a scattering angle γ, ω_a is the aerosol single scattering albedo, and r is Fresnel reflectance of the interface for a given incident angle.

Following the work of [13] , who have shown that for near-infrared channels the water leaving radiance coming out of clear open ocean waters can be assumed to be near zero because of strong water absorption, and if the effect of sun glitter is also assumed to be negligible, as in the case of OCM sensor which has provision for tilting mechanism to avoid sun glint [8] , then Equation (16) can be written as:

(18)

Therefore, the effects of aerosols, in the imagery can be estimated at the two NIR bands of 740 and 856-nm from the sensor-measured radiances and the computed Rayleigh scattering reflectance. This quantity is then extrapolated and removed in the visible bands of OCM data. Let us assume that the path reflectance at two bands in the NIR at and, where, and, can be estimated from the Equation

(18). Given that can be precisely calculated given the surface atmospheric pressure and therefore and can be determined from Equation (18) at and. This allows estimation of the parameter as:

(19)

This parameter is subsequently used to compute spectral variation, , of aerosol properties in the shorter wavelengths. The value of for the OCM band is calculated from, this yields, which when combined with, provides the desired path radiance in λ_i wavelength. Clearly, the key to this procedure is the estimation of from. The aerosol reflectance, , in the i^th wavelength is calculated by using the following equation:

(20)

Extrapolation of aerosol properties from to, which involves more than a factor of two in wavelengths has been studied by [11] . This study has provided detailed insight into the possible spectral behaviour of. They have computed for several aerosol models. Three basic aerosol models namely; the tropospheric model with no oceanic contribution; the maritime model for which 99% of the particles have the tropospheric characteristics and 1% the Oceanic; and the Coastal model for which 99.5% of the particles have the tropospheric characteristics and 0.5% the oceanic. This model was introduced to represent the aerosol over the oceans nearer the coast (less Oceanic contribution). The properties of all the three aerosol models depend on the wavelength and relative humidity. Sample results from this study for, where is taken to be 865 nm (OCM band 8), are redrawn from [11] in Figure 4. These results suggest that there is a strong variation of ε with aerosol model and relative humidity. The increase in the particle size (due to swelling) with increasing relative humidity clearly reduces the spectral variation of ε. They have shown that over the range 412 - 865 nm can be considered to be an exponential function of, for the [18] aerosol models and [11] have used these results for the extension of CZCS atmospheric correction algorithm for use with SeaWiFS and MODIS. The best-fit equation can be written as:

(21)

where

(22)

where, is the Rayleigh and ozone corrected aerosol radiances computed from the satellite image data. This algorithm is mainly valid for open ocean (case 1 water) where the assumption of for NIR bands holds well. However, this is not true in the case of turbid coastal waters in which the water leaving reflectance at NIR bands are often not negligible. Further the estimated water-leaving reflectance are converted to normalised

water-leaving reflectance, , which is earlier defined as

(23)

where, is the atmospheric diffuse transmittance in the solar direction with the solar zenith angle of.

The estimated value of normalized water-leaving reflectance values in different spectral bands can then be used to generate ocean-colour products such as chlorophyll concentration.

7.3. Atmospheric Correction Output

Output of the atmospheric correction algorithm will be used for bio-optical variable generation and output will be the normalized water-leaving radiance/remote-sensing reflectance, R_rs, in the OCM-2 spectral bands of 412, 443, 490, 510, 555, and 620-nm. Quality indices or flags, such as for negative water-leaving/remote sensing reflectance, clouds, sun-glint mask and turbid water, will also be produced.

8. Aerosol Optical Depth (AOD) over Oceans at 865-nm

Aerosols are responsible for a number of physical effects in the atmosphere, the most important being modifying the atmospheric radiation balance [19] by reflecting away the incoming solar radiation and retaining the outgoing terrestrial radiation (greenhouse effect). Aerosols also reduce visibility, cause air pollution and influence the cloud formation microphysics by acting as condensation nuclei. Satellites, with their capability for large area coverage and short-term repeativity, are the most ideal means for acquiring global information on aerosols [20] [3] . The currently orbiting ocean colour sensors like Oceansat-1 OCM, SeaWiFS, MODIS and MERIS though primarily meant for ocean colour remote sensing, have the additional capability for monitoring of global distribution of marine aerosols.

Space borne ocean-colour remote sensor detected radiance is heavily contaminated by solar radiation backscattered by the atmosphere air molecules & aerosols. This radiance is called the atmospheric radiance. So for the detection of the oceanic constituents first step is therefore the removal of the atmospheric contribution from the sensor radiances. For this NIR channel (l > 700 nm) is used as ocean surface acts as a dark background due to the high absorption by water. Therefore the sensor-detected radiances can be considered as the atmospheric radiance, which can be treated just the sum of the Rayleigh & Aerosol path radiance produced by the scattering of light by air molecules & aerosols. So according to [15] radiances detected by a space borne sensor at top of atmosphere (TOA) at wavelength l > 700 nm can be split into

(24)

where,

L_t = Sensor detected radiance;

is Aerosol path radiance.

is Rayleigh path radiance.

where, F_o is Extra terrestrial solar flux.; J_v is Satellite viewing angle; w_oa is Aerosol single scattering albedo; w_or is Rayleigh single scattering albedo (~1.0); t_a is Aerosol optical depth; t_r is Rayleigh optical depth; P_a(J) function related to Aerosol scattering Phase function; P_r(J) function related to Rayleigh scattering Phase function. This P_a(J)/P_r(J) related to the Aerosol/Rayleigh scattering Phase function according to [15] is given as

(25)

where,

R(J_v) Frensel reflectance of the water surface along (J_v) satellite viewing angle.

R(J_s) Frensel reflectance of the water surface along (J_s) solar zenith angle.

J^± represents the Forward (+)/Backward (−) scattering angle.

The scattering angles in direction to the sensor and in direction to the sensor via the air-sea interface is given as

(26)

where, f is the azimuth difference between the sensor viewing and solar illumination direction.

The Rayleigh Phase function is computed by following equation

(27)

The aerosol phase function can be approximated by the two-term Henyey-Greenstein phase function:

(28)

with α = 0.985, g₁ = 0.8, g₂ = 0.5 for marine aerosols [15] .

For calculating the specular reflectance at the air-sea interface R(J_v) and R(J_s), we need the law of refraction (Snell’s law):

(29)

where n is the refractive index of water, i the incident zenith angle J_v or J_s and j the zenith angle of the refracted beam under water and n the refractive index, which is for water 4/3, and the Fresnel law for unpolarized light which is:

(30)

Assuming w_oa » 1.0 for marine aerosols, we can determine the aerosol optical depth (AOD) from the sensor detected radiance as

(31)

This algorithm was also successfully used by [20] with Oceansat-1 OCM data for the estimation of AOD over the oceanic areas and now the same algorithm is used with Oceansat-2 OCM data. Figure 5 shows the flow chart for the computation of the bio-optical and atmospheric parameters from the Oceansat-2 OCM data.

As OCM-2 has two day repetivity two day composite of the successive two day passes are sufficient to cover the entire north Indian Ocean (NIO). However, it needs one week passes to generate a single global coverage AOD product to cover the entire global oceans. As a example of weekly (8-day) composite and monthly composites covering the north Indian Ocean and global oceans are shown in Figure 6(a) and Figure 6(b) respectively.

9. Conclusion

In this present study the methodology and the processing scheme for estimating the aerosol optical depth (AOD)

at 865 nm from Oceansat-2 Ocean Colour Monitor (OCM) has been explained. From this study it is clear that OCM-2 derived AOD products are highly useful for studying the atmospheric turbidity and plays an important role in generating the accurate geophysical products. The LAC and GAC AOD products of OCM-2 show a very good spatio-temporal variability over the north Indian Ocean and over the global oceans respectively. Further these AOD products over the north Indian Ocean needs to be intercompared and validated with the existing contemporary ocean colour sensors.

Acknowledgements

The authors would like to thank the ISRO’s Earth Observations (EO) missions for providing the consistent ocean colour data and SeaDAS development group at NASA GSFC for providing the standard SeaDASv6.4 and the recent version 7 for processing OCM-2 data. We Thank Dr. Prakash Chauhan, Space Applications Centre, Ahmedabad for providing valuable information on Indian Ocean Colour sensors and the retrieval strategy.

Cite this paper

Udaya LakshmiSriperambudur,ChandralingamSonnati,Nagamani PullaiahgariVenkata,Preethi LathaThalathoti, (2015) Retrieval of Aerosol Optical Depth from Oceansat-2 OCM. Open Journal of Marine Science,05,443-454. doi: 10.4236/ojms.2015.54035

References