World Journal of Neuroscience
Vol.3 No.3(2013), Article ID:34919,14 pages DOI:10.4236/wjns.2013.33021
A Clifford algebraic analysis gives mathematical explanation of quantization of quantum theory and delineates a model of quantum reality in which information, primitive cognition entities and a principle of existence are intrinsically represented ab initio*
![]()
1School of International Advanced Studies on Applied Theoretical and Non Linear Methodologies of Physics, Bari, Italy
2Department of Neurosciences and Sense Organs, University of Bari “Aldo Moro”, Bari, Italy
Email: elio.conte@fastwebnet.it
Copyright © 2013 Elio Conte. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 7 April 2013; revised 20 May 2013; accepted 24 June 2013
Keywords: Information; Quantum Cognition; Principle of Existence; Quantum Mechanics; Quantization; Clifford Algebra; Cognitive Sciences
ABSTRACT
The thesis of this paper is that Information, Cognition and a Principle of Existence are intrinsically structured in the quantum model of reality. We reach such evidence by using the Clifford algebra. We analyze quantization in some traditional cases of quantum mechanics and, in particular in quantum harmonic oscillator, orbital angular momentum and hydrogen atom. The results are confirmed analyzing human cognition behavior that evidences a very consistent agreement with the basic quantum mechanical foundations.
1. INTRODUCTION
The earliest versions of quantum mechanics were formulated in the first decade of the 20th century following about the same time the basic discoveries of physics as the atomic theory and the corpuscular theory of light that was basically updated by Einstein. Early quantum theory was significantly reformulated in the mid-1920s by Werner Heisenberg, Max Born and Pascual Jordan, who created matrix mechanics, Louis de Broglie and Erwin Schrodinger who introduced wave mechanics, and Wolfgang Pauli and Satyendra Nath Bose who introduced the statistics of subatomic particles. Finally, the Copenhagen interpretation became widely accepted but with profound reservations of some distinguished scientists and, in particular, A. Einstein who prospected the general and alternative view point of the hidden variables, originating a large debate about the conceptual foundations of the theory that has received in the past years renewed strengthening with Bell theorem [1], and still continues in the present days. By 1930, quantum mechanics was further unified and formalized by the work of David Hilbert, Paul Dirac and John von Neumann, [2] with a greater emphasis placed on measurement in quantum mechanics, the nature of reality and of its knowledge, involving the debate also a large body of epistemological and philosophical interest. Another feature that has always characterized the debate on quantum mechanics has been that one to identify what is the best mathematics that we should use in order to prospect quantum reality.
Conventionally formulated quantum mechanics starts always with the combined standard mathematical, well known, description from one hand and the use of classical physical analogies on the other hand.
Our position is that by this way we risk to negate the fundamental nature of quantum reality that is fixed on some basic and unclassical features. They are the integer quanta, the non commutation, the intrinsic-irreducible intedeterminism and quantum interference. It is possible to demonstrate that quantization, non commutation, intrinsic and irreducible indetermination, and quantum interference may be also obtained in a rough scheme due to the outset of the basic axioms of Clifford algebra.
First, let us follow the illuminating thinking of P. Dirac.
As previously said, P. A. M. Dirac contributed at the highest level to the final formulation of quantum mechanics. In his “The Development of Quantum Theory” [3] and “History of Twentieth Century Physics” [4], he wrote:
“I saw that non commutation was really the dominant characteristic of Heisenberg’s new theory. It was really more important than Heisenberg’s idea of building up the theory in terms of quantities closely connected with experimental results. So I was led to concentrate on the idea of non commutation. I was dealing with these new variables, the quantum variables, and they seemed to be some very mysterious physical quantities and I invented a new word to describe them. I called them q-numbers and the ordinary variables of mathematics I called cnumbers to distinguish them… Then I proceed to build up a theory of these q-numbers. Now, I did not know anything about the real nature of these q-numbers. Heisenberg’s matrices, I thought, were just an example of qnumbers, may be q-numbers were really something more general. All that I knew about q-numbers was that they obeyed an algebra satisfying the ordinary axioms except for the commutative axiom of multiplication. I did not bother at all about finding a precise mathematical nature of q-numbers”.
Our approach may be reassumed as it follows.
Initiating with 2010 [5,6] we started giving proof of two existing Clifford algebras, the  that has isomorphism with that one of Pauli matrices and the
that has isomorphism with that one of Pauli matrices and the 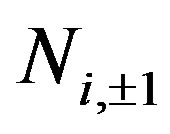 where
where 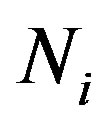 stands for the dihedral Clifford algebra.
stands for the dihedral Clifford algebra.
The salient feature is that we showed that the 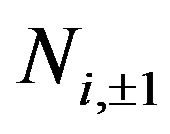 may be obtained from the
may be obtained from the  algebra when we attribute a numerical value (+1 or −1) to one of the basic elements
algebra when we attribute a numerical value (+1 or −1) to one of the basic elements  of the
of the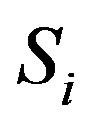 . We utilized such result to advance a criterium under which the
. We utilized such result to advance a criterium under which the 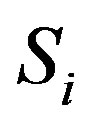 algebra has as counterpart the description of quantum systems that in standard quantum mechanics are considered in absence of observation and quantum measurement while the
algebra has as counterpart the description of quantum systems that in standard quantum mechanics are considered in absence of observation and quantum measurement while the 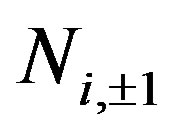 attend when a quantum measurement is performed on such system with advent of wave function collapse.
attend when a quantum measurement is performed on such system with advent of wave function collapse.
The physical content of the criterium is that the quantum measurement and wave function collapse induce the passage in the considered quantum system from the  to
to 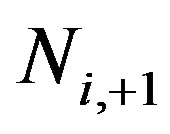 or to the
or to the 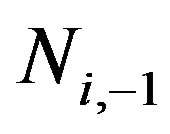 algebras, where each algebra has of course its proper rules of commutation. On this basis we re-examined the von Neumann postulate on quantum measurement, and we gave a proper justification of such postulate by using the
algebras, where each algebra has of course its proper rules of commutation. On this basis we re-examined the von Neumann postulate on quantum measurement, and we gave a proper justification of such postulate by using the . algebra. We also studied some direct applications of the above mentioned criterium to some cases of interest in standard quantum mechanics, analyzing in particular a two state quantum system, the case of time dependent interaction of such system with a measuring apparatus and finally the case of a quantum system plus measuring apparatus developed at the order n = 4 of the considered Clifford algebras and of the corresponding density matrix in standard quantum mechanics. In each of such cases examined, we found that the passage from the algebra
. algebra. We also studied some direct applications of the above mentioned criterium to some cases of interest in standard quantum mechanics, analyzing in particular a two state quantum system, the case of time dependent interaction of such system with a measuring apparatus and finally the case of a quantum system plus measuring apparatus developed at the order n = 4 of the considered Clifford algebras and of the corresponding density matrix in standard quantum mechanics. In each of such cases examined, we found that the passage from the algebra 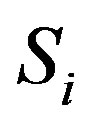 to
to , considered during the quantum measurement of the system, actually describes the collapse of the wave function. Therefore we concluded that the actual quantum measurement has as counterpart in the Clifford algebraic description, the passage from the
, considered during the quantum measurement of the system, actually describes the collapse of the wave function. Therefore we concluded that the actual quantum measurement has as counterpart in the Clifford algebraic description, the passage from the  to the
to the 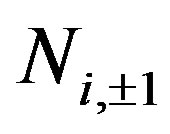 Clifford algebras, reaching in this manner the objective to reformulate von Neumann postulate on quantum measurement and proposing a self-consistent formulation of quantum theory. We reached also another objective. The combined use of the
Clifford algebras, reaching in this manner the objective to reformulate von Neumann postulate on quantum measurement and proposing a self-consistent formulation of quantum theory. We reached also another objective. The combined use of the 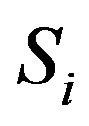 Clifford algebra and the
Clifford algebra and the 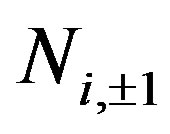 dihedral Clifford algebra, also accomplishes to another basic requirement that the advent of quantum mechanics strongly outlined. Heisenberg initial view point was to modify substantially our manner to look at the reality. He replaced numbers by actions as also outlined by Stapp [7]; a number represents the manner in which the dynamics of a given object has happened. Heisenberg replaced such standard view point requiring instead that we have to explicit the mathematical action (let us remember that the notion of operator will be subsequently adopted), and this action becomes the mathematical counterpart of the physical corresponding action whose outcome will give a number as final determination. Such double features of standard quantum mechanics represent of course a basic and conceptually profound innovation in our manner to conceive reality and the methodology to investigate it. It is clearly synthesized in our Clifford algebraic formulation by using from one hand the Clifford
dihedral Clifford algebra, also accomplishes to another basic requirement that the advent of quantum mechanics strongly outlined. Heisenberg initial view point was to modify substantially our manner to look at the reality. He replaced numbers by actions as also outlined by Stapp [7]; a number represents the manner in which the dynamics of a given object has happened. Heisenberg replaced such standard view point requiring instead that we have to explicit the mathematical action (let us remember that the notion of operator will be subsequently adopted), and this action becomes the mathematical counterpart of the physical corresponding action whose outcome will give a number as final determination. Such double features of standard quantum mechanics represent of course a basic and conceptually profound innovation in our manner to conceive reality and the methodology to investigate it. It is clearly synthesized in our Clifford algebraic formulation by using from one hand the Clifford 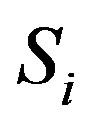 and, as counterpart, the
and, as counterpart, the 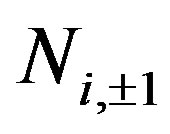 dihedral Clifford algebra.
dihedral Clifford algebra.
Generally speaking, our general position is that quantization, non commutation, intrinsic-irreducible indetermination and quantum variables as new “mysterious physical quantities”, also if in a rough scheme, may be actually described and due to the outset of the basic axioms of Clifford algebra. This is the reason because we started in 1972 to attempt to formulate a bare bone skeleton of quantum mechanics by using Clifford algebra and on this basis we have obtained also some other interesting results. Rather recently, as example, we have obtained a very interesting feature that could be related to quantum reality. It is well known that J. von Neumann [2] constructed a matrix logic on the basis of quantum mechanics. In [8-10] we inverted the demonstration, we showed that quantum mechanics may be constructed from logic. This feature may represent a turning point. In fact, the evidence is that we have indication about the logical origin of quantum mechanics and by this way we are induced to conclude that quantum reality has intrinsically a new feature that we are not accustomed to attribute to it. Quantum reality starts admitting a role for logic, thus for cognition, language, semantic not in a foreseen sense. There is a principle in quantum reality that we are addressed to evidence in the following manner: there are stages of our reality (those engaged from quantum theory, precisely) in which matter no more may be conceived by itself, it no more may be conceived independently from the cognition that we have about it. This is a new viewpoint that involves mind like entities, modulating matter with cognition ab initio in our quantum reality. Therefore it opens a new way to acknowledge a role of quantum mechanics in cognitive sciences [11,12].
In previous papers we have investigated such our approach considering indeterminism and quantum interference The aim of the present paper is to add here new results to such thesis. We select to consider here the problem of the quantization.
2. THEORETICAL ELABORATION
Our basic statement is that quantum reality has its peculiar features.
Instead conventionally formulated quantum mechanics starts always with the use of classical analogies. Our approach is different. Our thesis is that by this way we risk to negate the fundamental nature of quantum reality that is fixed on three basic and unclassical features. They are the integer quanta, the non commutation, and the intrinsic-irreducible intedeterminism and quantum interference.
Quantization, non commutation and intrinsic and ireducible indetermination are actually evidenced by using the outset of the basic axioms of Clifford algebra. We have previously mentioned that, by using such algebraic elaboration, we realized a bare bone skeleton of quantum mechanics formulating in particular about the intrinsicirreducible indetermination shown from quantum reality and the relevant role of non commutation and quantum interference. We will not consider here further on such statements since they were discussed in detail by us previously [11,12].
Previously we did not consider the question of the integer quanta and we attempt to derive here a detailed exposition.
Let us sketch the problem remembering that in quantum mechanics some physical quantities may be expressed in the following manner
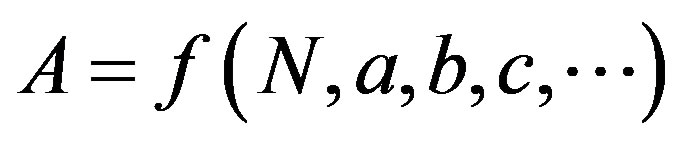 (2.1)
(2.1)
where  may be constants and N assumes only discrete, integer values
may be constants and N assumes only discrete, integer values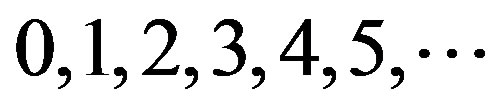 .
.
N may be conceived to be the following Clifford member of the  algebra that we have discussed elsewhere [5,6]
algebra that we have discussed elsewhere [5,6]
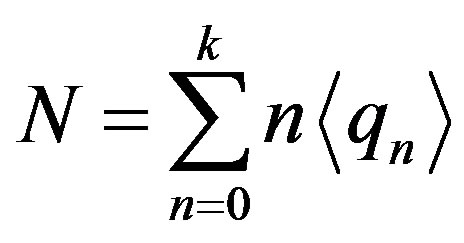 (2.2)
(2.2)
where 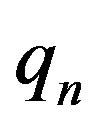 are specific Clifford members having some specific properties.
are specific Clifford members having some specific properties.
Let us consider the case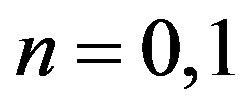 .
.
In this case  is given in the following manner
is given in the following manner
 (2.3)
(2.3)
where  and
and 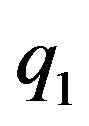 are the following idempotents in
are the following idempotents in 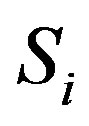
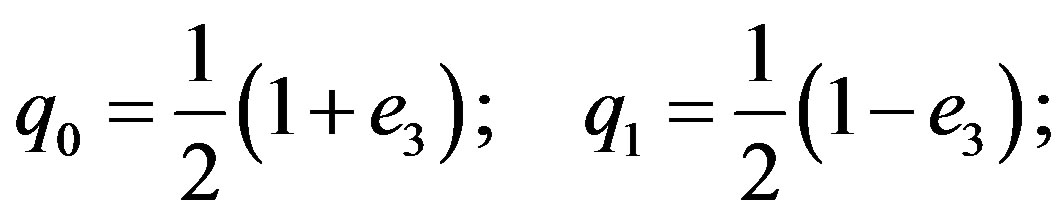 (2.4)
(2.4)
We have
 (2.5)
(2.5)
Let us write the mean value of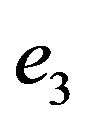 . It is
. It is
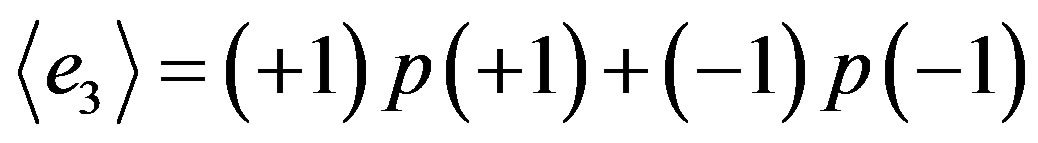 (2.6)
(2.6)
being  and
and 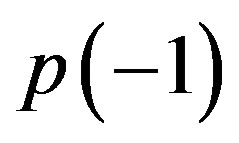 the corresponding probabilities for the abstract entity
the corresponding probabilities for the abstract entity 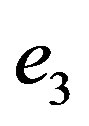 to assume or the numerical value
to assume or the numerical value  or the numerical value
or the numerical value 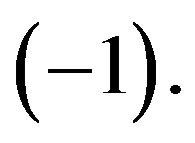
let us admit now that  is a cognitive entity. Of course we know that, according to von Neumann [2], density operators as well a correspondingly, idempotent elements may be considered logic statements.
is a cognitive entity. Of course we know that, according to von Neumann [2], density operators as well a correspondingly, idempotent elements may be considered logic statements.
Let us admit that the cognitive entity, represented by 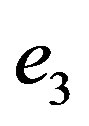 is in the condition of absolute certainty that the represented system
is in the condition of absolute certainty that the represented system  to which
to which 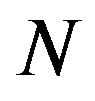 is connected, has the value
is connected, has the value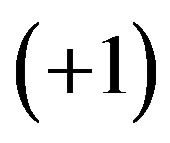 . This means in the (2.6) that
. This means in the (2.6) that 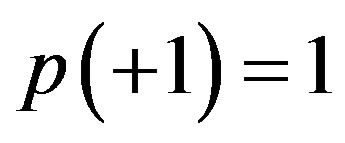 and
and . Consequently
. Consequently 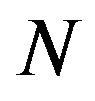 will be characterized from the discrete integer value
will be characterized from the discrete integer value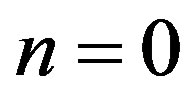 . In the other possible case,
. In the other possible case, 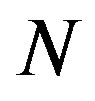 will be characterized from the discrete integer value
will be characterized from the discrete integer value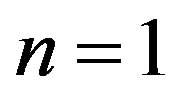 .
.
Speaking in general quantum terms, the question of interest is the immediate connection that we establish between the integer quantized condition of the physical observable that we have identified containing  and the cognitive task that must be performed. In order to ascertain the quantized integer value of
and the cognitive task that must be performed. In order to ascertain the quantized integer value of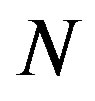 , a cognitive task must be performed in the sense that a semantic act is here clearly involved. Of course Orlov [13] was the first to identify
, a cognitive task must be performed in the sense that a semantic act is here clearly involved. Of course Orlov [13] was the first to identify  as the basic and universal logic operator. Still, the aim of the elaboration must be clear here. Certainly we do not speak here about human cognition but of primitive cognitive entities.
as the basic and universal logic operator. Still, the aim of the elaboration must be clear here. Certainly we do not speak here about human cognition but of primitive cognitive entities.
The relation of 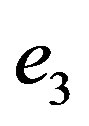 with the basic wave function of quantum mechanics is of course established.
with the basic wave function of quantum mechanics is of course established.
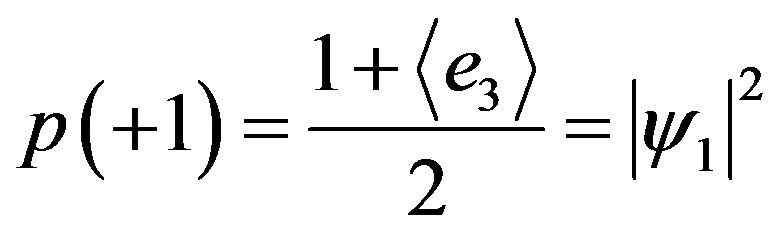 (2.7)
(2.7)
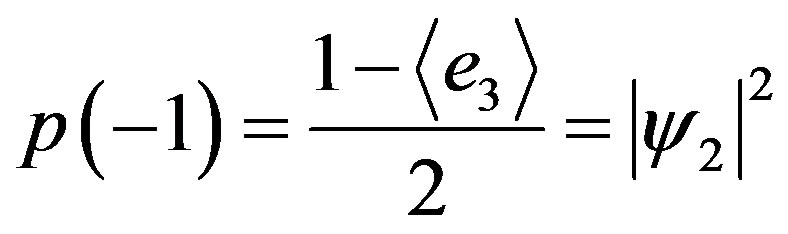 (2.8)
(2.8)
being 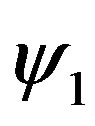 and
and 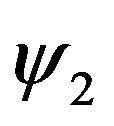 corresponding selected kets in the proper Hilbert space.
corresponding selected kets in the proper Hilbert space.
In conclusion we have given proof of a necessary and sufficient link existing between 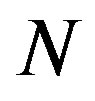 and
and .
.
We should write
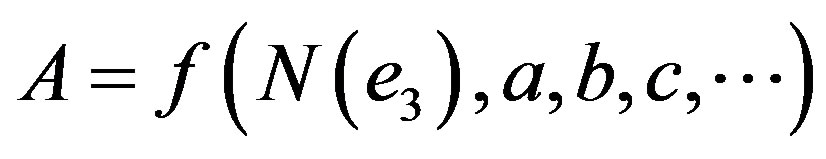 (2.9)
(2.9)
with
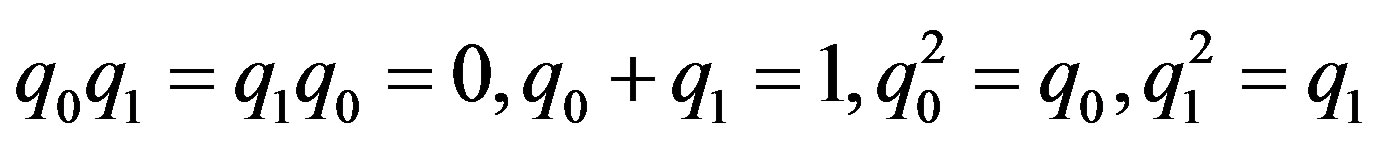 (2.10)
(2.10)
Let us examine what it happens in the case in which we consider N assuming four possible integer values.
In this case we need a Clifford algebraic structure given at the order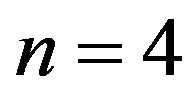 . The four possible combinations of the basic primitive idempotent elements are
. The four possible combinations of the basic primitive idempotent elements are
 ; (2.11)
; (2.11)
Note that in this case we invoke the basic and universal logic operators (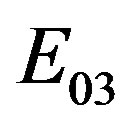 and
and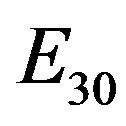 ) and the coupling (conjunction)
) and the coupling (conjunction) . Obviously, also the relations like the (2.10) hold in this extended case.
. Obviously, also the relations like the (2.10) hold in this extended case.
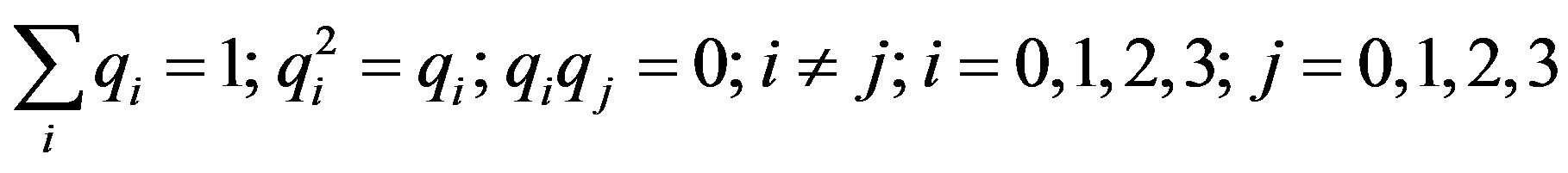 (2.12)
(2.12)
Let us apply now the previous criterium  that we considered previously.
that we considered previously.
Let us write the mean values of  and of
and of 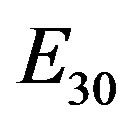 and
and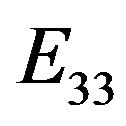 . It is
. It is
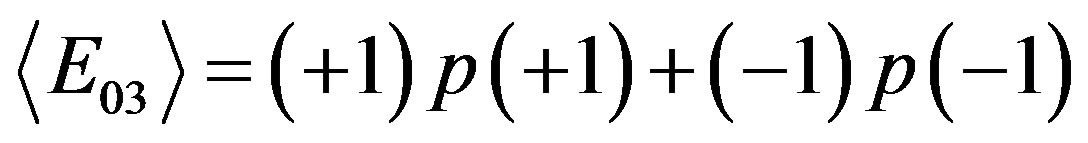 ; (2.13)
; (2.13)
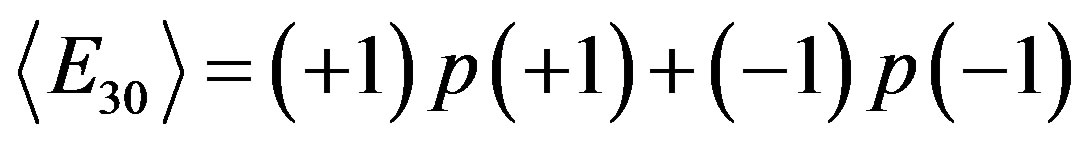 ; (2.14)
; (2.14)
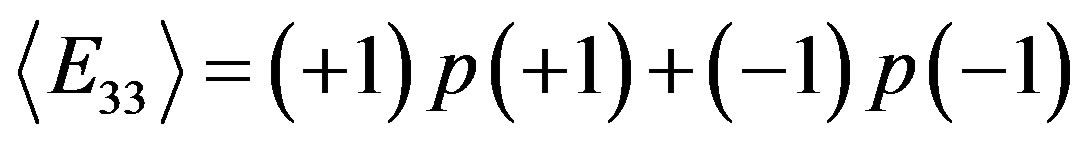 ; (2.15)
; (2.15)
being 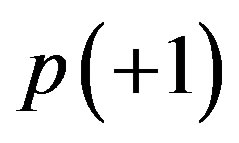 and
and 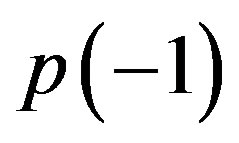 the corresponding probabilities for the abstract entities to assume or the numerical value
the corresponding probabilities for the abstract entities to assume or the numerical value  or the numerical value
or the numerical value 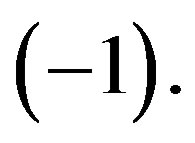
Let us admit now that ,
,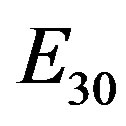 ,
, 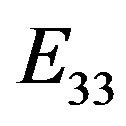 are cognitive entities. As previously said, we know that, according to von Neumann [16], density operators as well a correspondingly, idempotent elements may be considered logic statements.
are cognitive entities. As previously said, we know that, according to von Neumann [16], density operators as well a correspondingly, idempotent elements may be considered logic statements.
Let us admit that the cognitive entity, represented by  is in the condition of absolute certainty that the represented system S to which N is connected, has the value
is in the condition of absolute certainty that the represented system S to which N is connected, has the value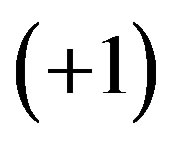 . This means in the (2.6) that
. This means in the (2.6) that  and
and . The same reasoning may be developed for
. The same reasoning may be developed for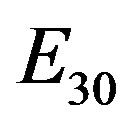 , and for
, and for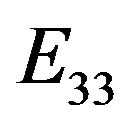 .
.
It results evident that by moving in this direction we are obtaining indication of a new arising scheme of reality. It seems that in substance the cognitive entities that we invoke here relate the same concept of existence. Is this existing condition of reality actually existing? The concept of Existence becomes here itself a variable that assumes therefore two possible values, indicating yes/not cognitive condition. Existence and cognition result therefore profoundly linked in the scheme of reality that we are delineating. The conceptual indication that we suggest here is that in the basic foundation of our reality ab initio there are elements of existence defined, not in terms of some hazy metaphysical concept of existence, but in the sense that existence, related to cognition, is represented by abstract entities of the Clifford algebra, and that contains only two possibilities: existence or nonexistence. A pure dichotomic variable structured in the inner architecture of our reality. Of course consciousness is awareness and knowledge about something existing. Certainly we have factors of scale so that a microstructure of our reality employs a limited number of abstract entities and a mechanism of amplification at a macrostructural level must be expected in order to account for awareness as it is usually intended at the level of human cognition, but it is clear that in any case we are speaking about a dynamics that starts as intrinsically conceived in the scheme of our reality from its starting ab initio. The idea of course is not new here. We think as example to Eddington [14] and to D. J. Bohm, P. G. Davies, H. J. Hiley [15]. Eddington in 1946 argued that within a purely algebraic approach, which he regarded as providing a structural description of physics, there are elements of existence defined, not in terms of some hazy metaphysical concept of existence, but in the sense that existence is represented by a symbol that contains only two possibilities: existence or non-existence. Just as in our treatment by using Clifford algebra, these authors assumed that the structural concept of existence is represented by an idempotent of some appropriate algebra and satisfying the conditions given by us in the (2.10) or in the (2.12).
Let us admit now that
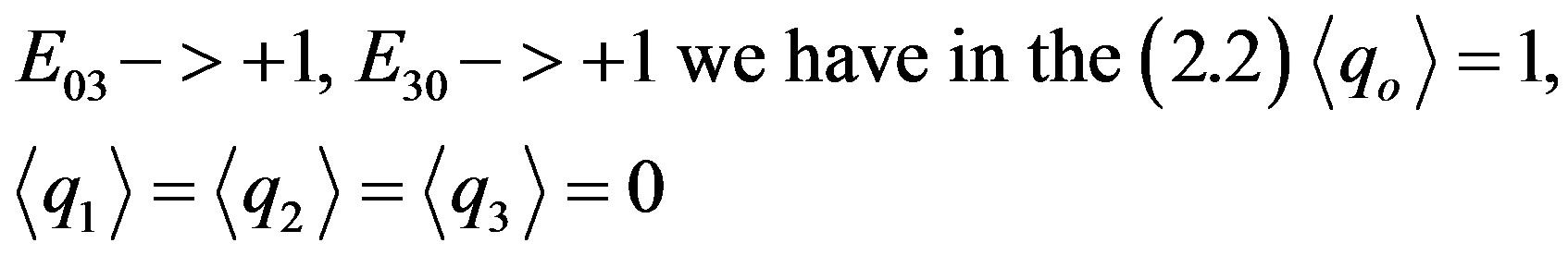 (2.16)
(2.16)
and the first integer value is obtained.
If instead the cognitive performance ascertains that
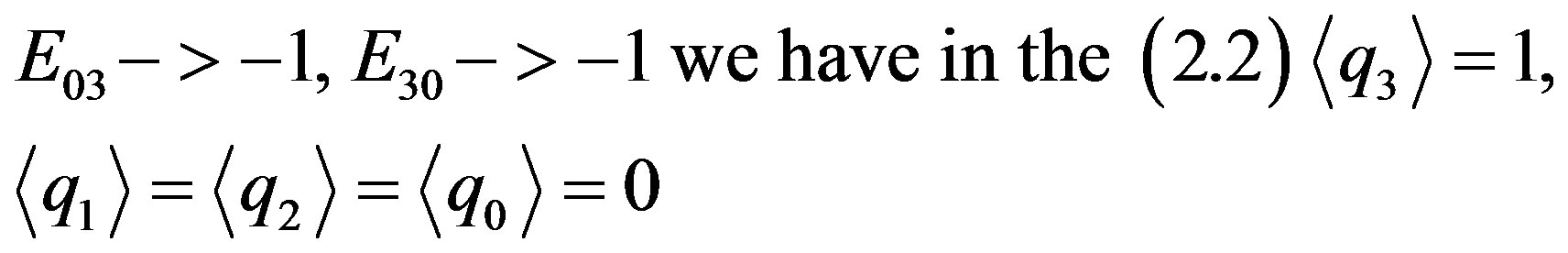 (2.17)
(2.17)
and the second integer is obtained.
In the case in which
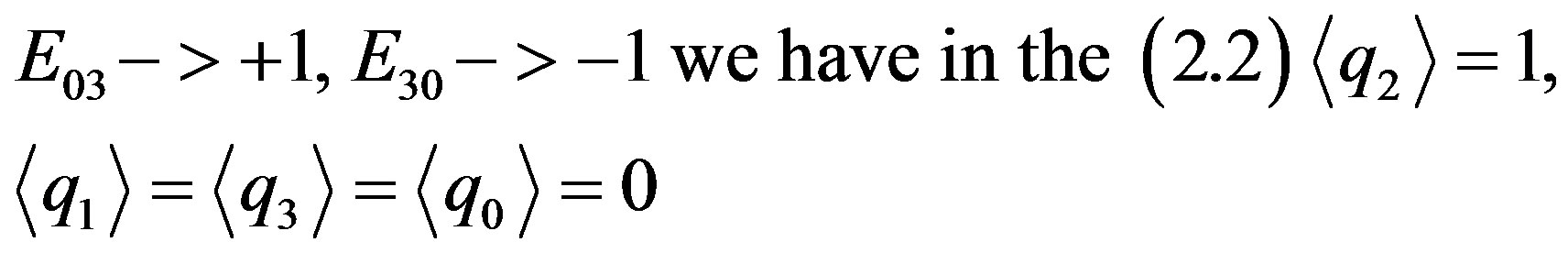 (2.18)
(2.18)
and the third integer is obtained Finally, with
 (2.19)
(2.19)
and the fourth integer is obtained.
Obviously the case of three integer is trivial and will not be discussed here.
The case 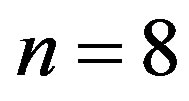 proceeds in the same manner.
proceeds in the same manner.
We need Clifford algebraic elements in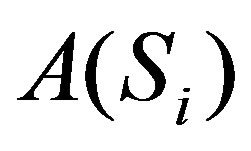 :
:
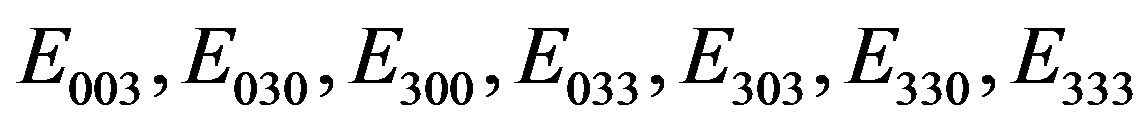 (2.20)
(2.20)
We may be sure that our Clifford algebraic structure at the order n = 8 will be
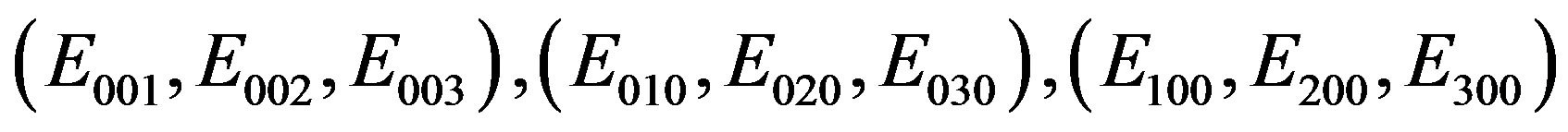 (2.21)
(2.21)
and related sets providing coupling.
In this case they give origin to the following basic Clifford elements
 (2.22)
(2.22)
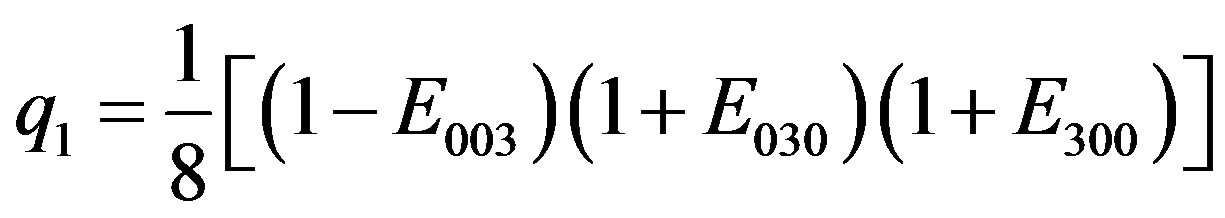 (2.23)
(2.23)
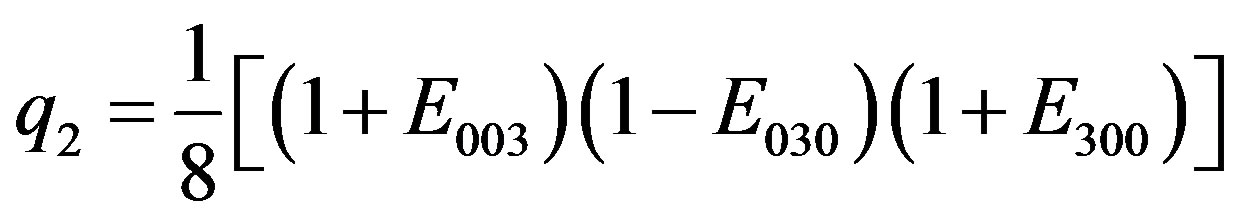 (2.24)
(2.24)
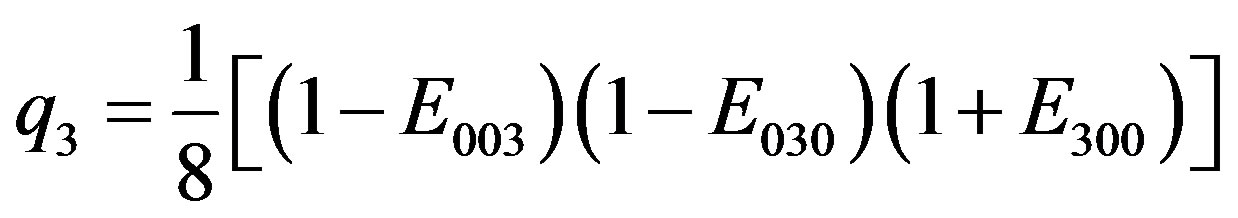 (2.25)
(2.25)
 (2.26)
(2.26)
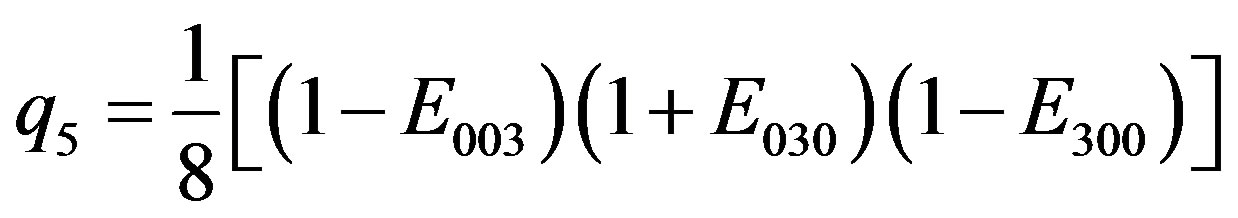 (2.27)
(2.27)
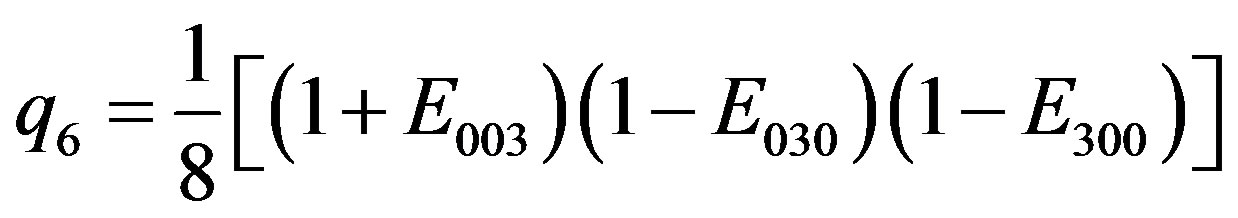 (2.28)
(2.28)
 (2.29)
(2.29)
Note the particular alternation in the signs of the idempotent elements arising for each  with i = 0, 1, ∙∙∙, 7.
with i = 0, 1, ∙∙∙, 7.
We have (+,+,+), (–,+,+), (+,–,+), (–,–,+), (+,+,–), (–,+,–), (+,–,–), (–,–,–). A combination of all the possible alternatives: a clear semantic message is contained and it is intrinsic to the inner structure of such arising integer quanta mechanism.
Obviously all such  satisfy the required rules given in the (2.12).
satisfy the required rules given in the (2.12).
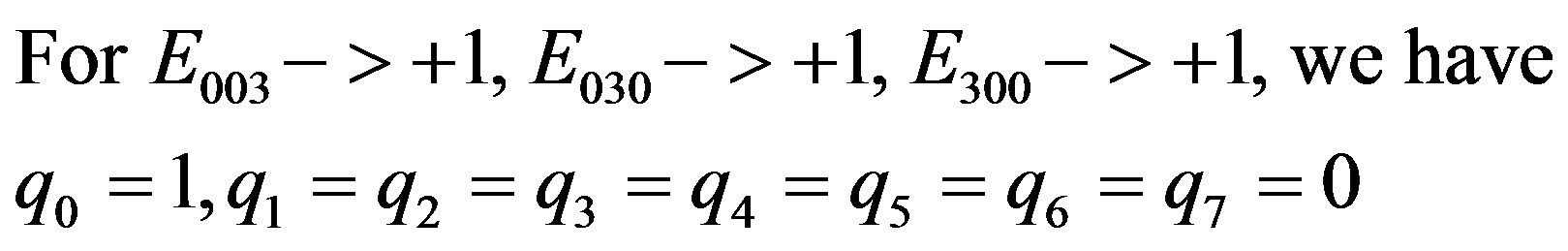 (2.30)
(2.30)
and the first integer value is obtained.
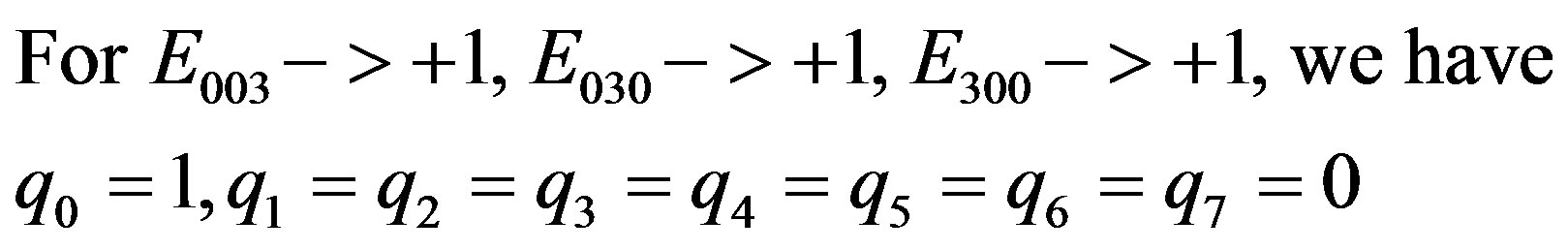 (2.31)
(2.31)
and the first integer value is obtained.
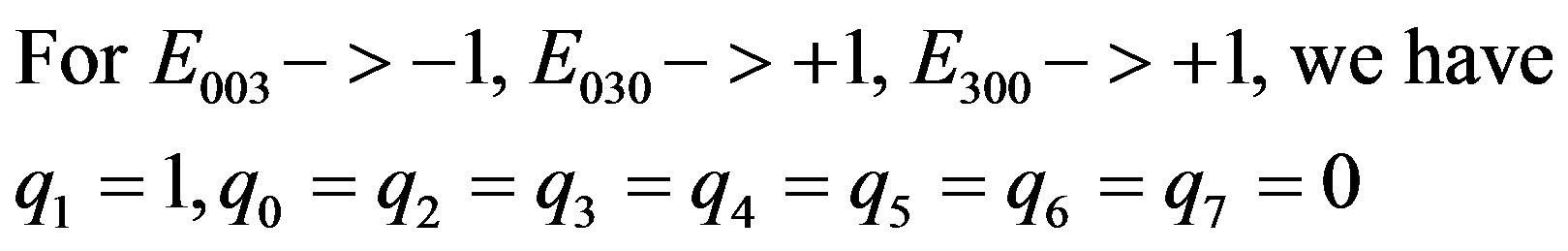 (2.32)
(2.32)
and the second integer value is obtained.
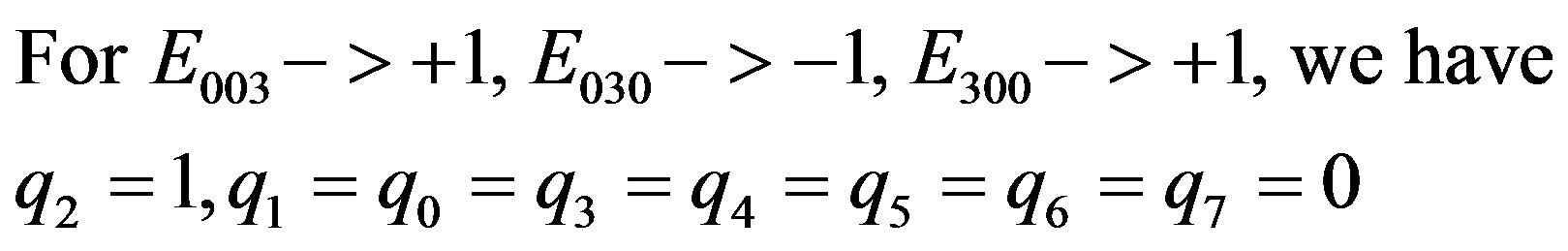 (2.33)
(2.33)
and the third integer value is obtained.
 (2.34)
(2.34)
and the fourth integer value is obtained.
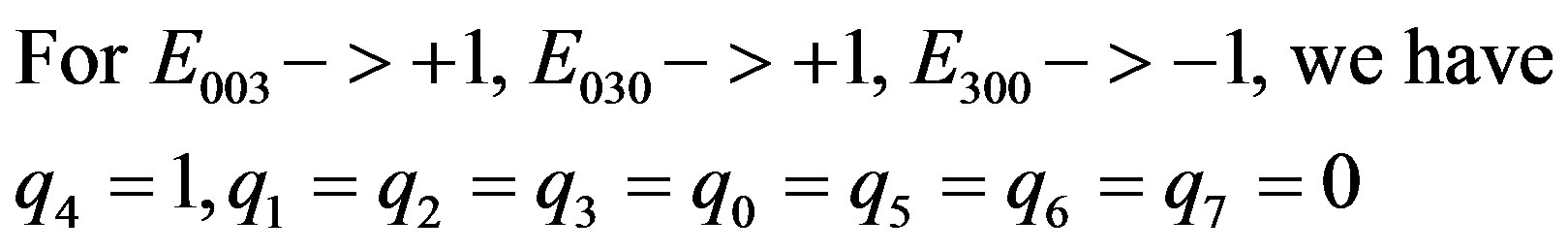 (2.35)
(2.35)
and the fifth integer value is obtained.
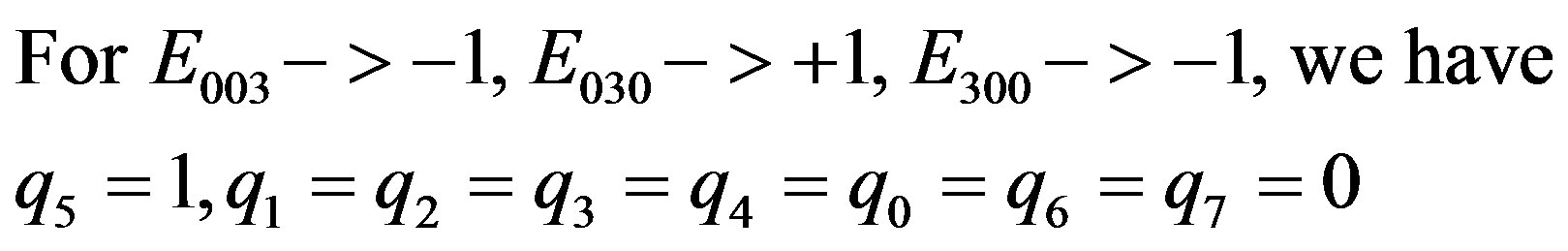 (2.36)
(2.36)
and the sixth integer value is obtained.
 (2.37)
(2.37)
and the seventh integer value is obtained.
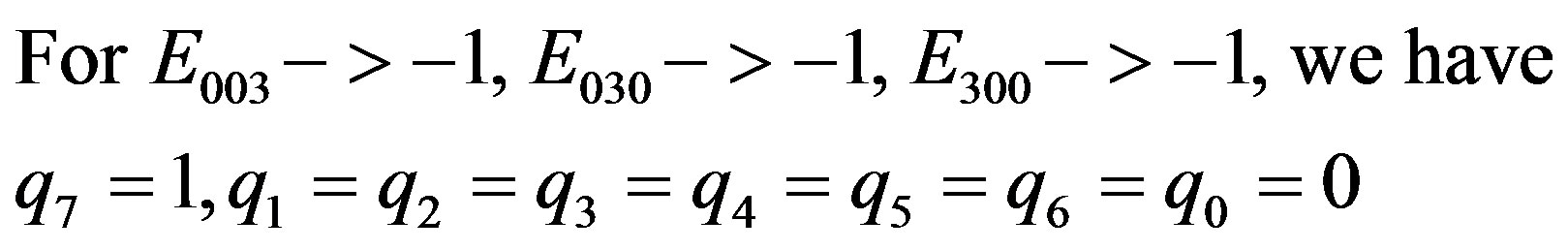 (2.38)
(2.38)
and the eighth integer value is obtained.
Corresponding to each value there is a clear condition of semantic awareness that is intrinsically linked.
We may now take a further step on.
It is well known that the Clifford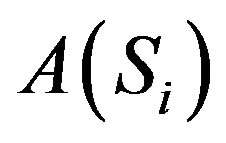 , in addition to admits idempotent, also contains nilpotent.
, in addition to admits idempotent, also contains nilpotent.
Generally speaking, it is known that an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0.
Previously we have considered two idempotent in 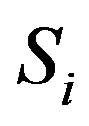 written as
written as 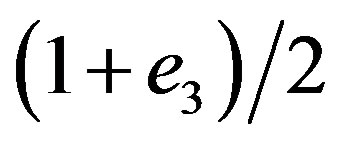 and
and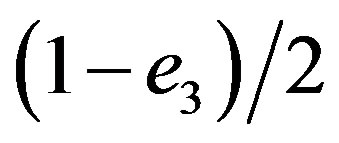 . In the same algebra two nilpotent can be written as
. In the same algebra two nilpotent can be written as 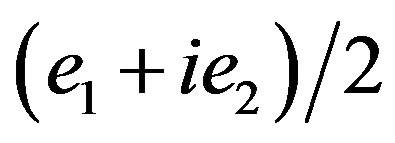 and
and 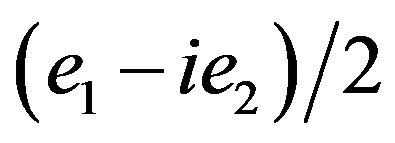 This is at the order
This is at the order 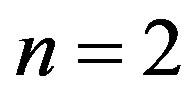 but we may easily generalize them at higher orders.
but we may easily generalize them at higher orders.
The important thing is to observe here that the two nilpotent elements may be rewritten linked to idempotent:
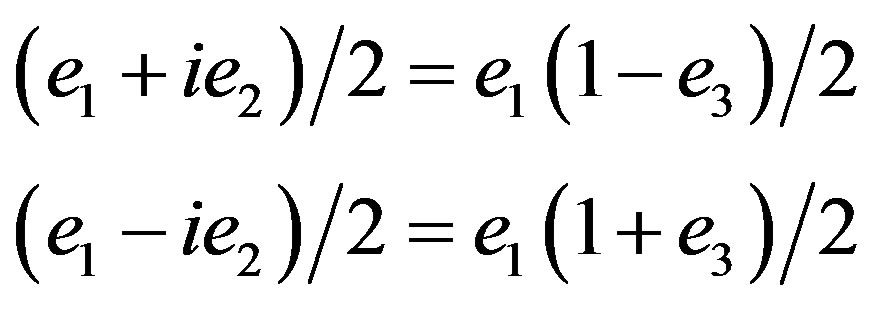 (2.39)
(2.39)
where we have used the Clifford representation of the imaginary unity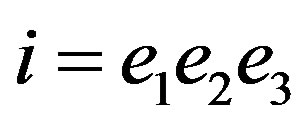 .
.
These nilpotent elements are the same as the idempotent elements multiplied by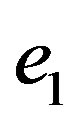 .
.
Still it is instructive to observe that
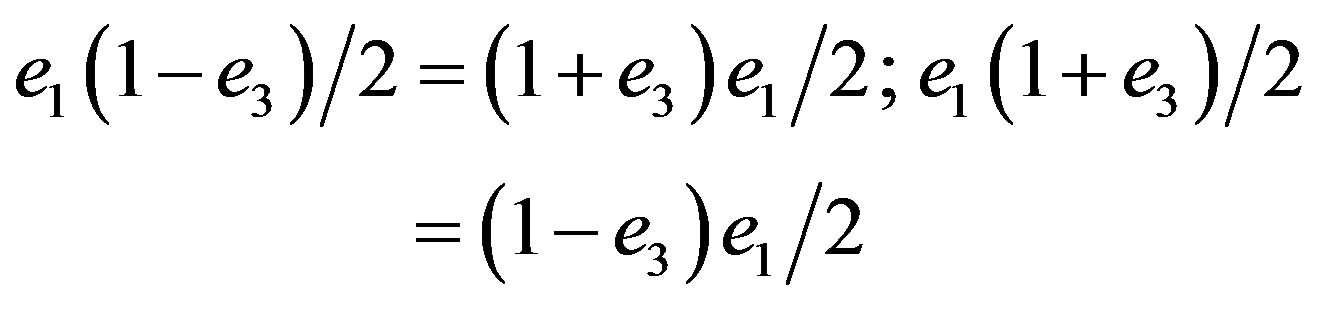 (2.40)
(2.40)
and
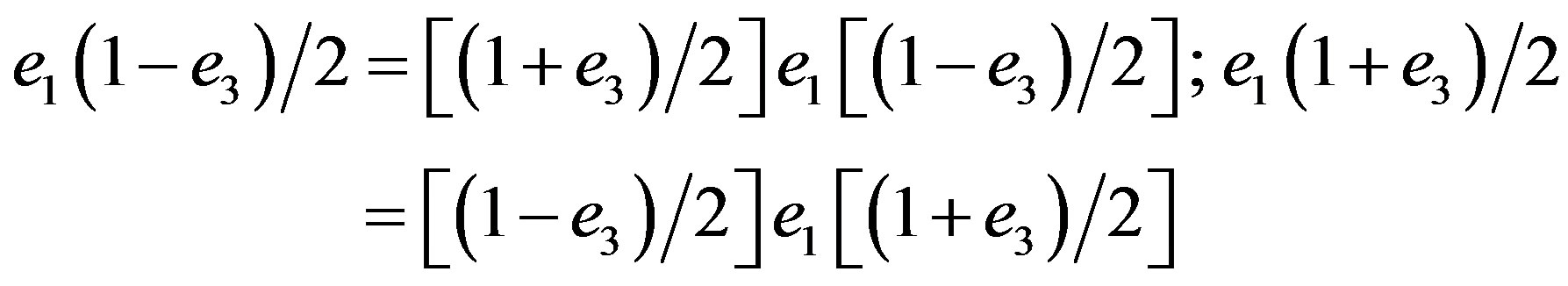 (2.41).
(2.41).
What is the reason to have introduced here the notion of nilpotent that of course is well known in Clifford algebra. The reason is that on the basis of the previously discussed link existing in our view point between idempotent elements, logic, semantic, information, and cognitive abstract entities, also on the other hand the existing link between idempotent and nilpotent elements, must be defined also under the profile of the logic, semantic, information, and cognition delineating what is the meaning of nilpotent. In our view point, the condition that there exists some positive integer n such that xn = 0, under the logic, semantic, and cognitive profile, means that at this order 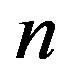 we reach an absurdum that our reality cannot admit.
we reach an absurdum that our reality cannot admit.
Let us consider now the following two basic nilpotent elements
 (2.42)
(2.42)
 is some prefixed real constant.
is some prefixed real constant.
Note that, in spite of being 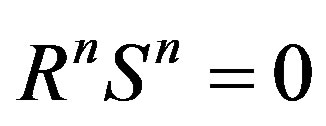 (absurdum) (
(absurdum) ( in the present case),
in the present case),
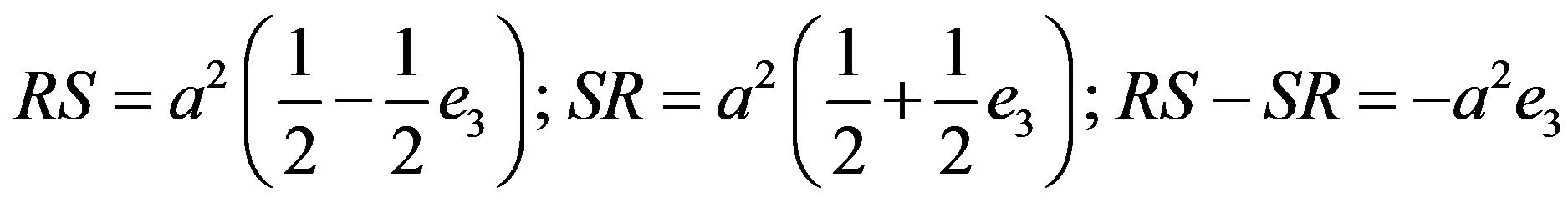 (2.43)
(2.43)
an idempotent element is instead obtained promptly at the order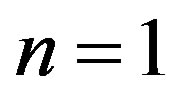 .
.
Let us admit to construct now some variables starting with  and
and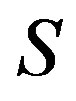 . In detail, let us introduce the variables
. In detail, let us introduce the variables  and
and  (Clifford algebraic elements) in the following manner
(Clifford algebraic elements) in the following manner
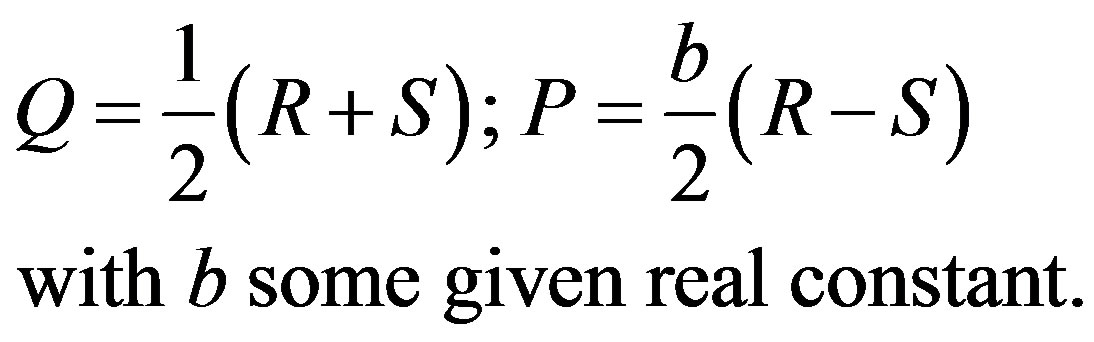 (2.44)
(2.44)
 (2.45)
(2.45)
Let us now examine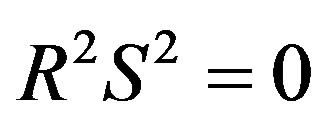 . It is
. It is
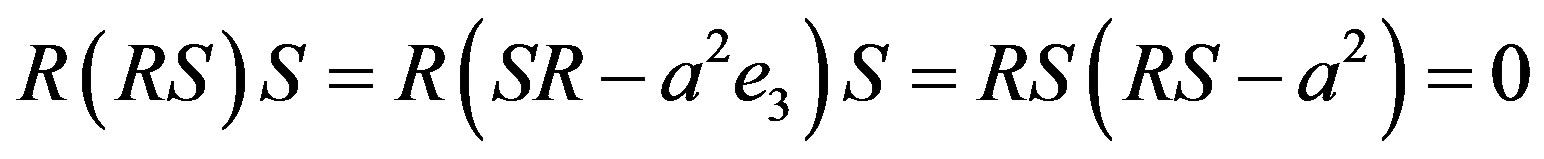 (2.46)
(2.46)
Let us write it explicitly. We obtain that
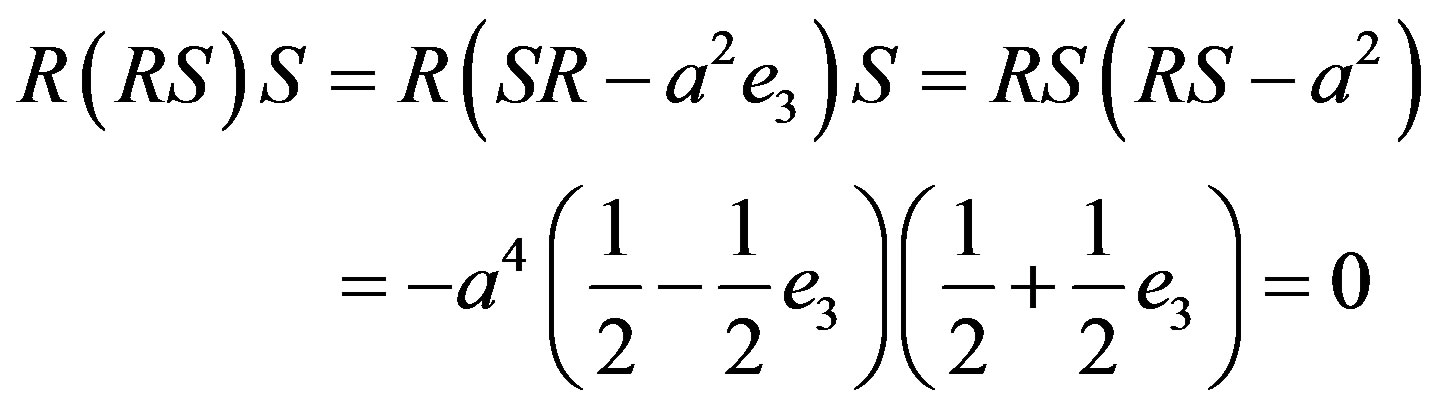 (2.47)
(2.47)
Two important results.
The first is that 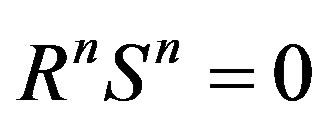
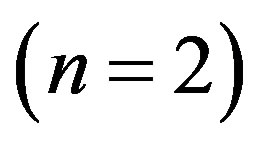 , starting with nilpotent elements for R and S, have been reduced again to idempotent elements (logic statements). The second is that we have obtained a tautology. The (2.47) is always true in itself, when we consider
, starting with nilpotent elements for R and S, have been reduced again to idempotent elements (logic statements). The second is that we have obtained a tautology. The (2.47) is always true in itself, when we consider 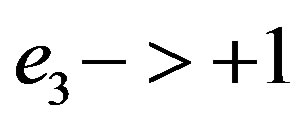 as well as when we consider
as well as when we consider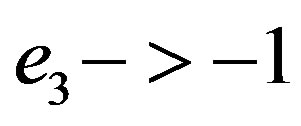 .
.
The procedure is now well fixed. We may proceed discussing the case at the order .
.
We know by now the basic sets of Clifford elements that we have to recall (see the (2.20)) and in this case we have
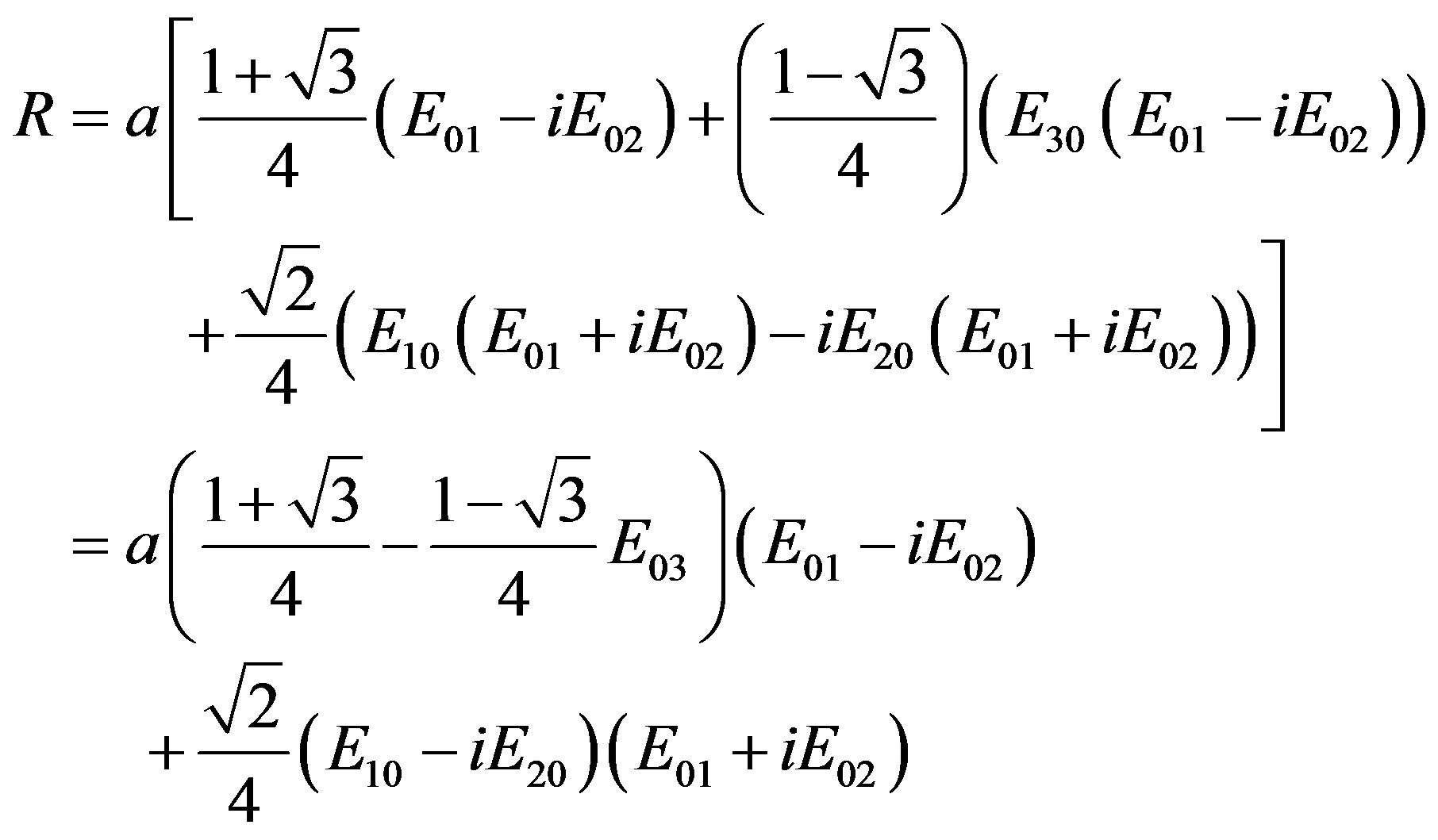 (2.48)
(2.48)
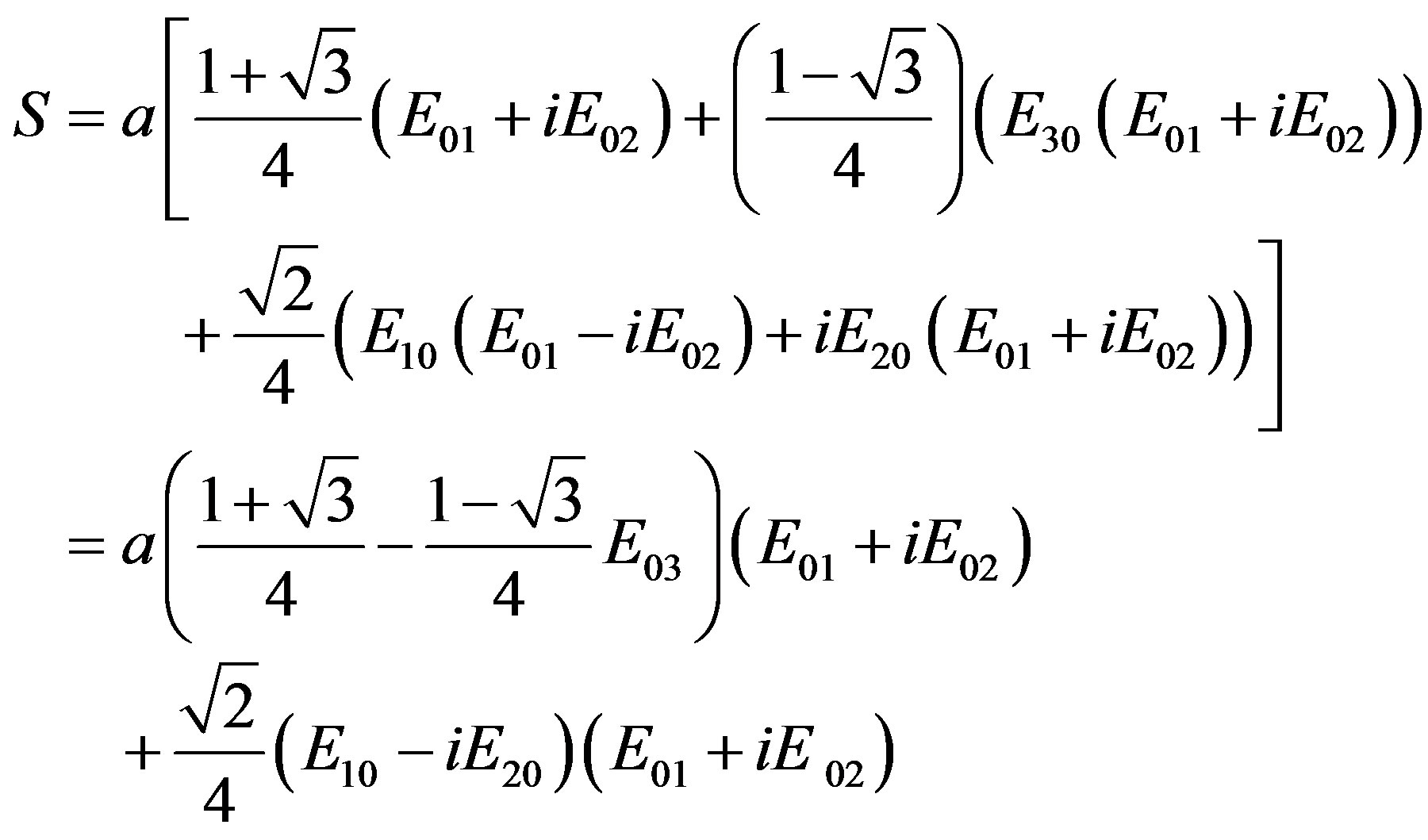 (2.49)
(2.49)
and the argument proceeds as in the previous case, this time at order  and thus having RnSn = 0; Rn−1Sn−1 ¹ 0 with
and thus having RnSn = 0; Rn−1Sn−1 ¹ 0 with .
.
In each case nilpotent elements are finally reduced to idempotent elements indicating logical statements.
What is then the interesting feature of the procedure that we have here developed. It is not only in the matter to have used pure Clifford members and to have discussed about their logic, and thus semantic, cognitive feature. The substantial result is that such cognitive features are linked to matter as it is in the thesis of our papers. In fact let us take 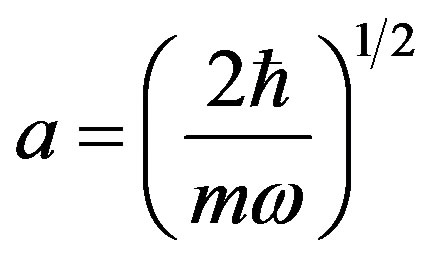 in the starting (2.42) and
in the starting (2.42) and  in the starting (2.44). Consider the Clifford elements
in the starting (2.44). Consider the Clifford elements  and
and  to represent the position and the momentum of a particle signed by the Hamiltonian
to represent the position and the momentum of a particle signed by the Hamiltonian
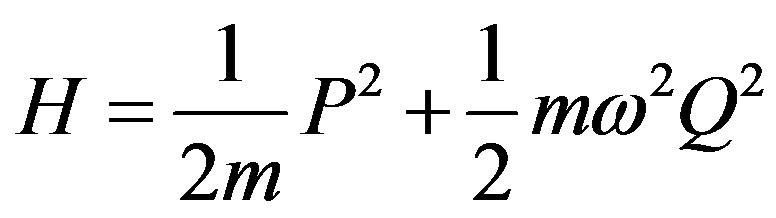 (2.50)
(2.50)
We are examining now the well known case of the harmonic oscillator in standard quantum mechanics.
As it is well known, the quantized oscillator energy is given by
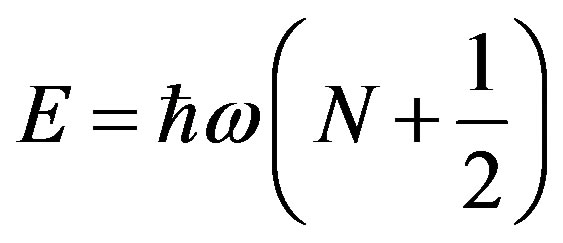 . (2.51)
. (2.51)
In this case it results
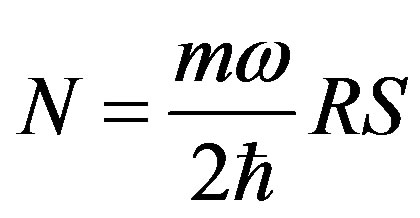 (2.52)
(2.52)
and the quantized levels are obtained from the (2.46) at order 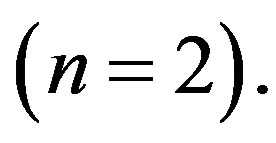 The following energy levels are obtained at the order (n = 4), (n = 8), and so on.
The following energy levels are obtained at the order (n = 4), (n = 8), and so on.
We have in this case a direct connection between logic statements, semantics, cognition from one hand and a material object as a quantum harmonic oscillator on the other hand. Of course, we have to outline here the basic conceptual foundation that the harmonic oscillator develops in the whole profile of quantum mechanics starting with the original and initial results of Heisenberg and arriving also to the most recent applications of the harmonic oscillators in the current days of application of quantum mechanics.
The same results may be obtained if we study quantization of orbital angular momentum or the hydrogen atom.
Relating orbital angular momentum, it is well known that
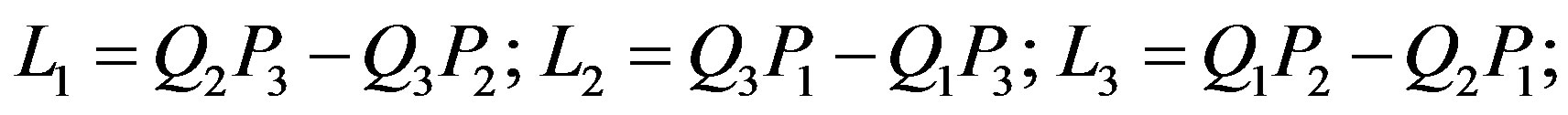 (2.53)
(2.53)
with
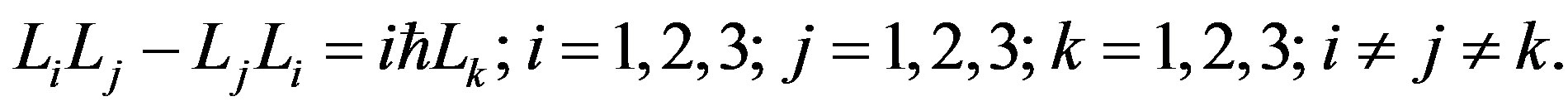 (2.54)
(2.54)
At just derived previously, at the order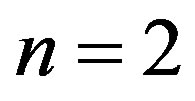 , we have the basic Clifford elements previously discussed for quantization
, we have the basic Clifford elements previously discussed for quantization
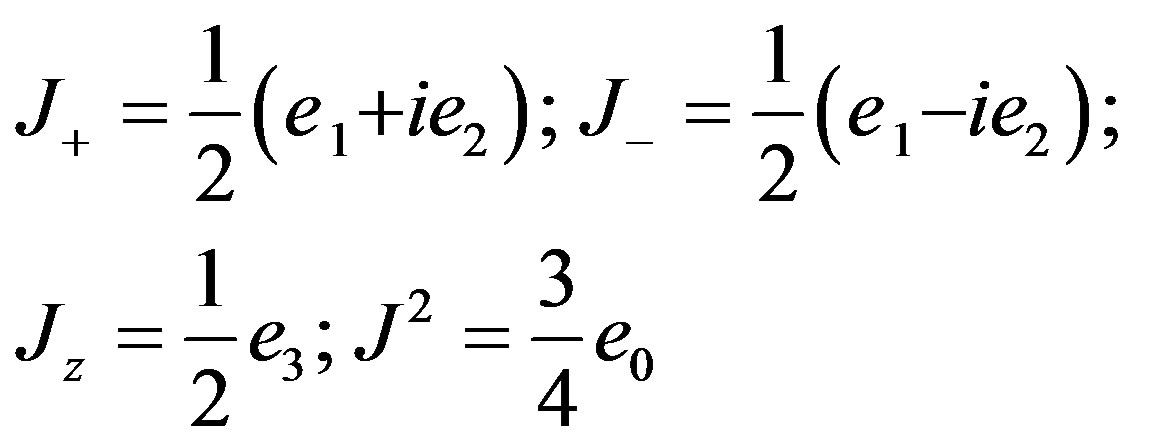 (2.55)
(2.55)
All the usual commutation relations of standard quantum mechanics are verified.
At the order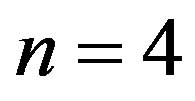 , we have
, we have
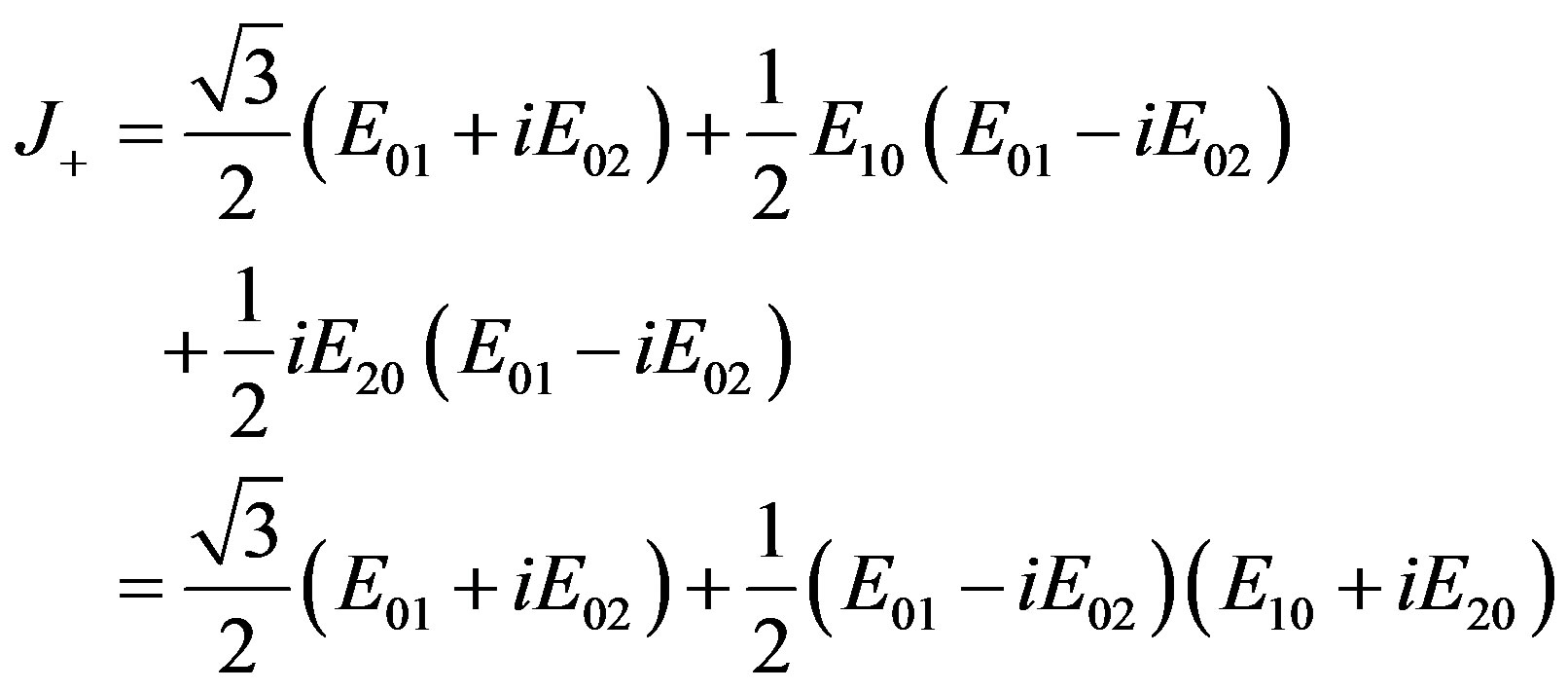 (2.56)
(2.56)
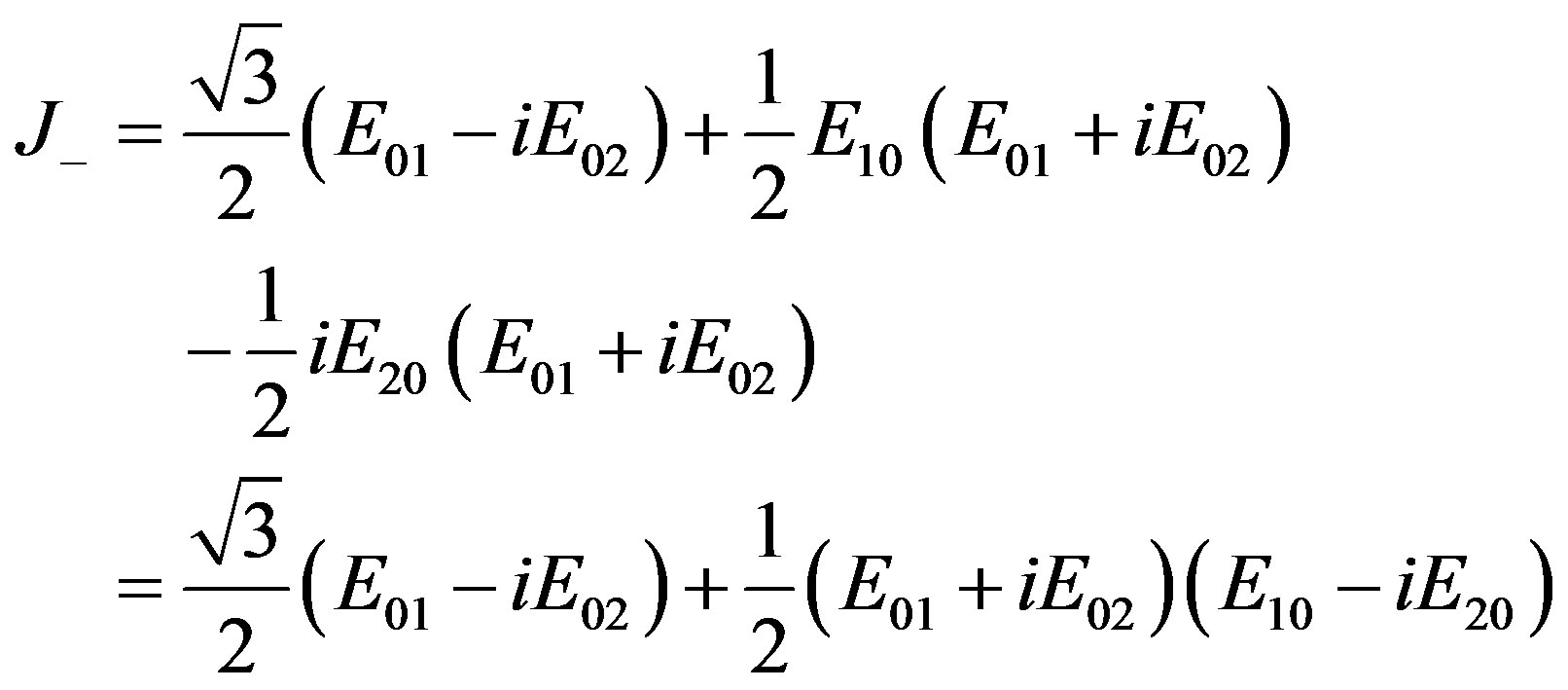 .(2.57)
.(2.57)
Again we have obtained the basic result. 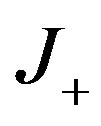 and
and 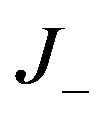 contain idempotent elements that are expression of logic statement. In fact we have that
contain idempotent elements that are expression of logic statement. In fact we have that
 ;(2.58)
;(2.58)
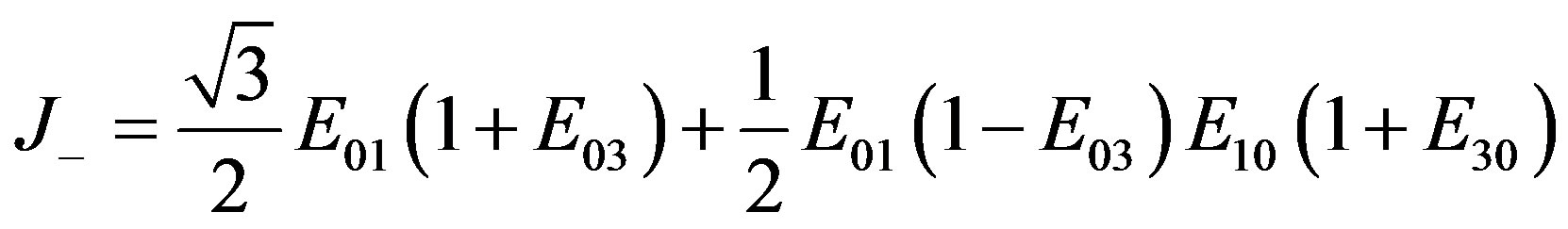 .(2.59)
.(2.59)
Our basic objective is reached also in this case.
Of course, the procedure of quantization is obtained following the same procedure outlined in the case of the harmonic oscillator using nilpotent elements that finally result expressed by idempotent elements and thus logical statements.
At the order 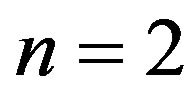 as well as at the order
as well as at the order  we obtain the basic relation
we obtain the basic relation
 (2.60)
(2.60)
that gives origin to the quantization.
We have that
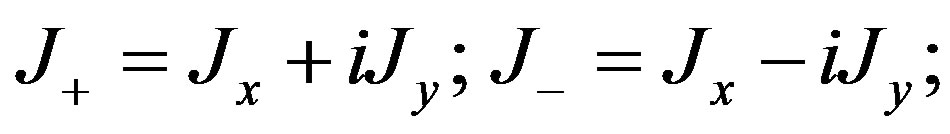 (2.61)
(2.61)
 (2.62)
(2.62)
 ; (2.63)
; (2.63)
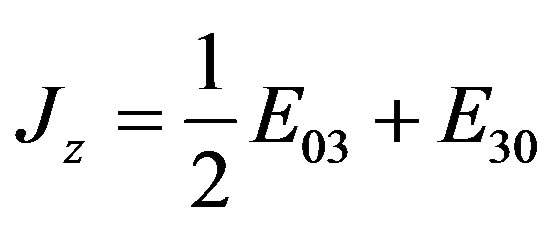 ; (2.64)
; (2.64)
with
 (2.65)
(2.65)
Note that we have
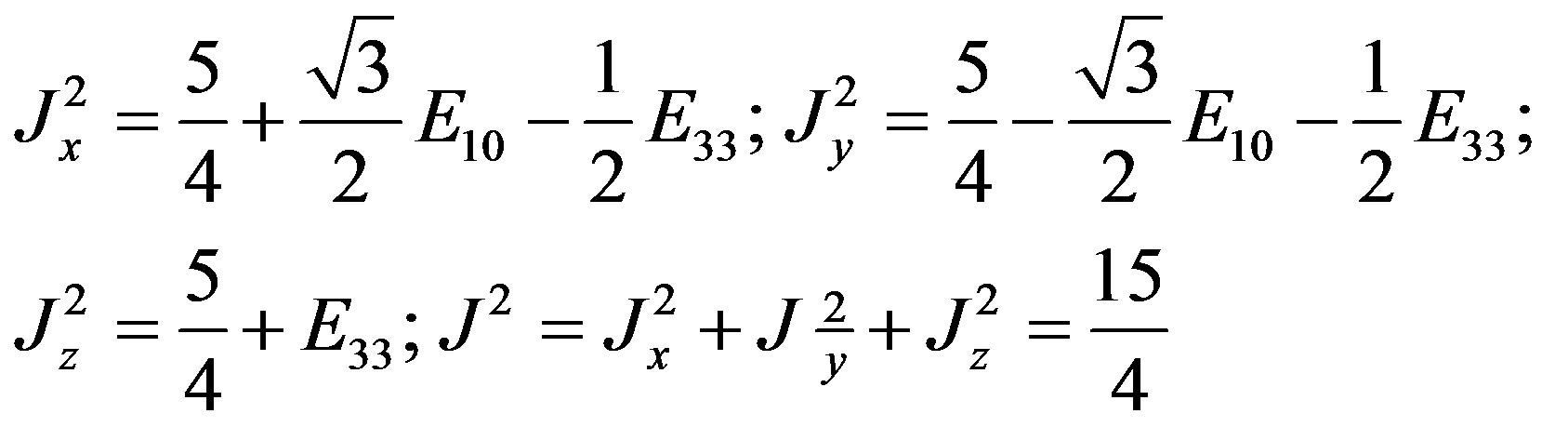 (2.66)
(2.66)
When passing In the Clifford algebra , we have that for
, we have that for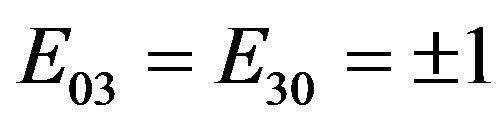 ,
, 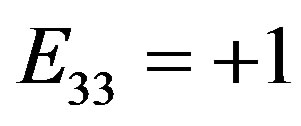 , it is
, it is
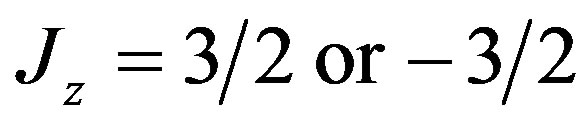 .
.
For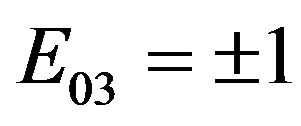 ,
,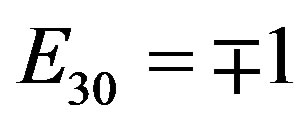 ;
;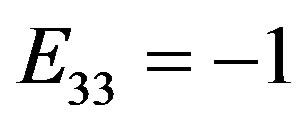 ,
,

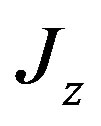 may assume one of the following numbers:
may assume one of the following numbers: 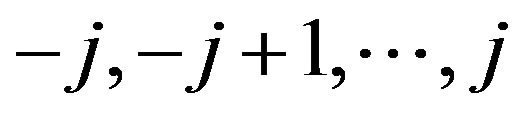 for
for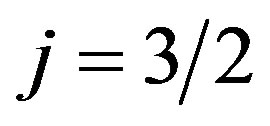 .
. 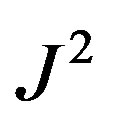 assumes the possible values
assumes the possible values 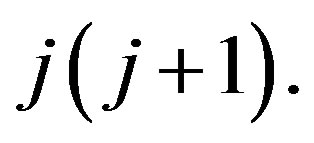
As required in our formulation we have that
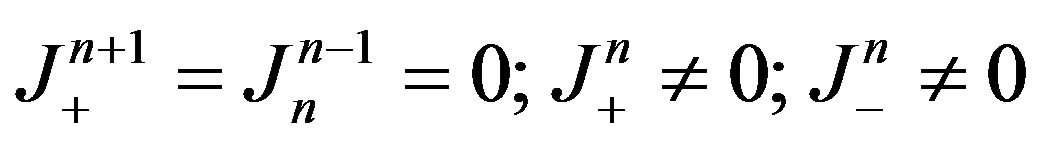 (2.67)
(2.67)
Therefore our basic formulation fixed on nilpotent and idempotent Clifford algebraic elements is again recalled.
It remains only a feature that needs to be explained. When considering , as said in the (2.65), we obtain
, as said in the (2.65), we obtain
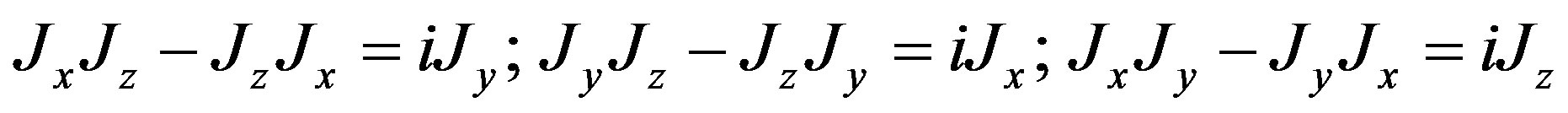 (2.68)
(2.68)
that do not correspond to the standard basic Clifford algebra 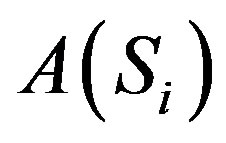 where in fact we have that
where in fact we have that
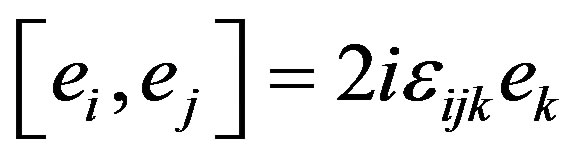 being the difference by a factor 2.
being the difference by a factor 2.
We gave detailed proof on the existence of the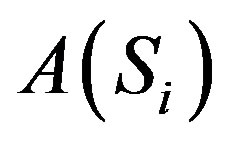 . The new algebra connected to the (2.68) may be demonstrated following the same procedure (see the [3,4]) and obtaining in this case the new basic elements
. The new algebra connected to the (2.68) may be demonstrated following the same procedure (see the [3,4]) and obtaining in this case the new basic elements
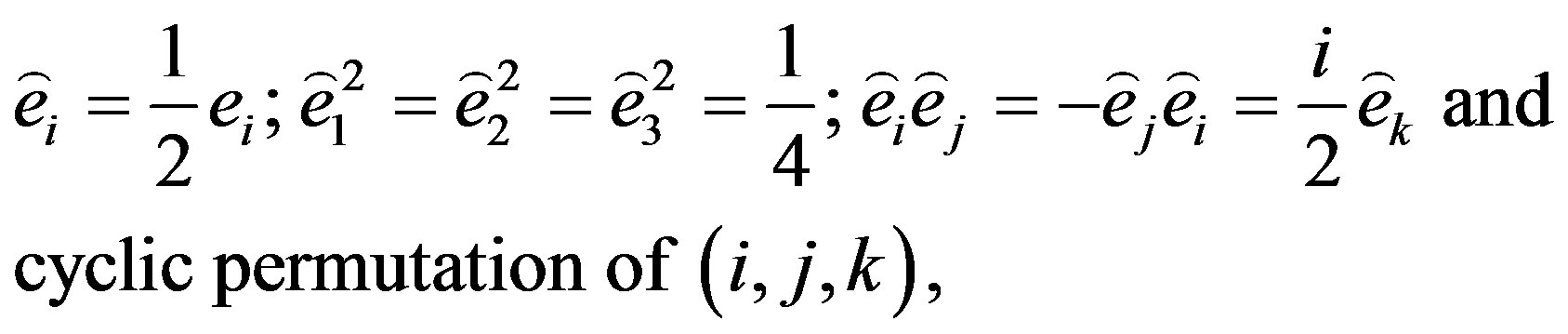 (2.69)
(2.69)
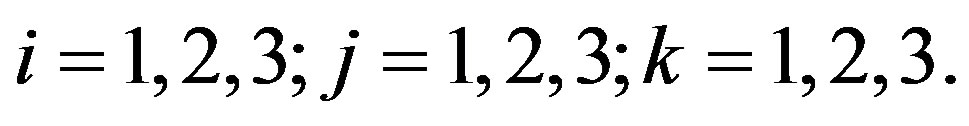
Idempotent elements become in this case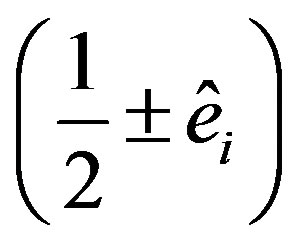 .
.
We may now pass to explore the quantization of the energy levels for the hydrogen atom.
The history of the first elaboration of quantum mechanics, relating in particular the study of the hydrogen atom, is well known.
The theory of Fourier and the correspondence principle of Bohr played a vital role in Heisenberg’s development of quantum mechanics. In essence, Heisenberg replaced the Fourier series by a ‘‘Fourier table’’. In his classic paper, each quantum formula was carefully crafted from the corresponding classical formula [16]. For Heisenberg, the problem with classical mechanics was not the dynamics, but the kinematics. According to Heisenberg, the equations of quantum mechanics are relations between observable quantities such as the spectral frequencies and intensities, and not the mechanical properties of the electron motion such as the position and period. Instead of representing x(t) by a sum of Fourier harmonics,
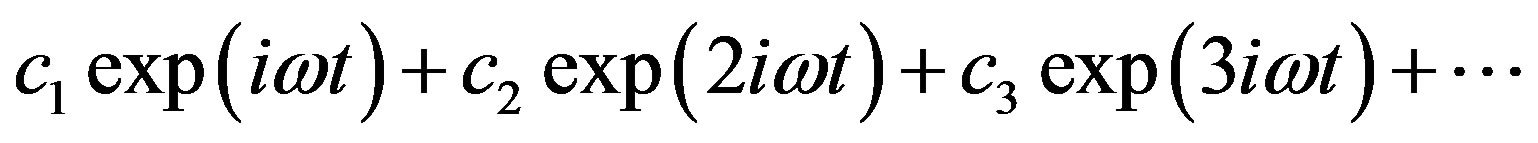 (2.70)
(2.70)
following the basic indications of Born, Pauli and Jordan, the dynamical variable x was finally represented by a matrix of Heisenberg harmonics,
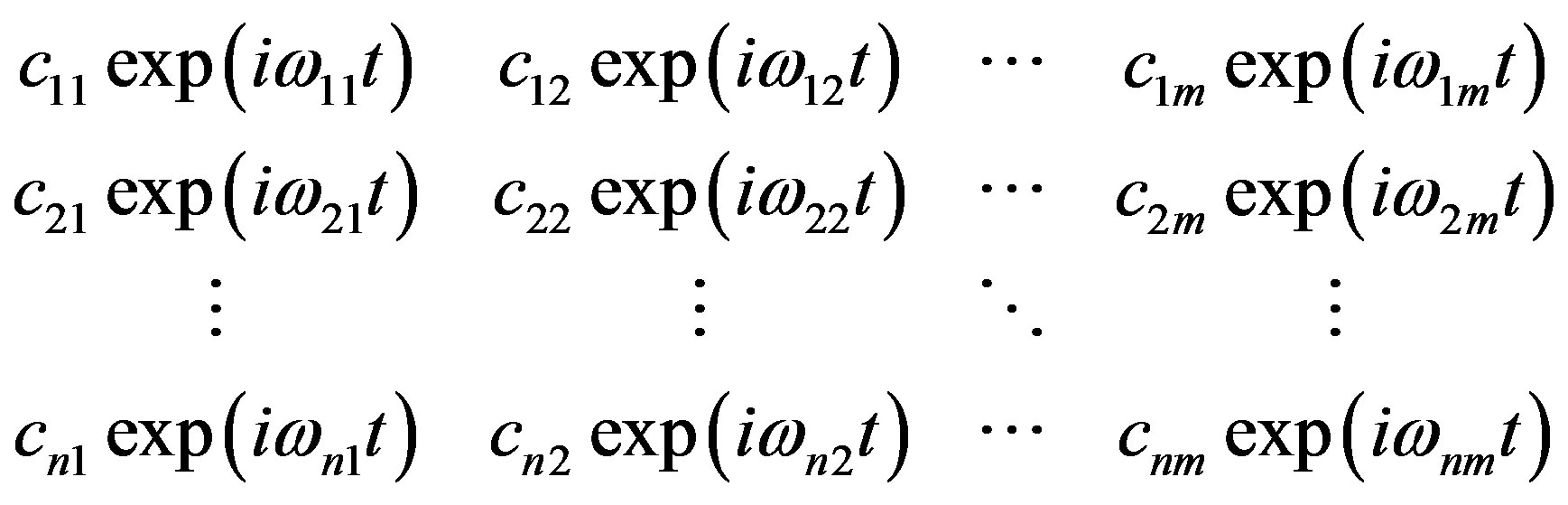
 (2.71)
(2.71)
The Heisenberg harmonic,  , is associated with the transition
, is associated with the transition  while the transition amplitude
while the transition amplitude 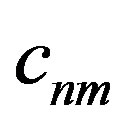 provides a measure of the intensity of the light and the transition frequency
provides a measure of the intensity of the light and the transition frequency 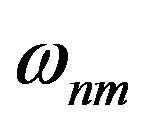 equals the light frequency. In particular, the Heisenberg harmonic
equals the light frequency. In particular, the Heisenberg harmonic 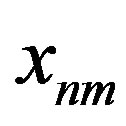 uniquely determines the transition probability
uniquely determines the transition probability 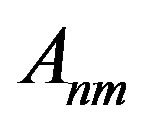 and the Power
and the Power 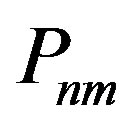 so that a net connection between the quantum mechanical motion of the electron
so that a net connection between the quantum mechanical motion of the electron 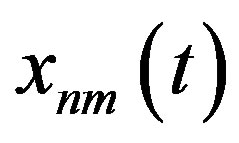 (the state of the electron) and the spectroscopic observable
(the state of the electron) and the spectroscopic observable 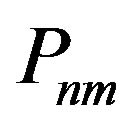 is strongly established:
is strongly established:
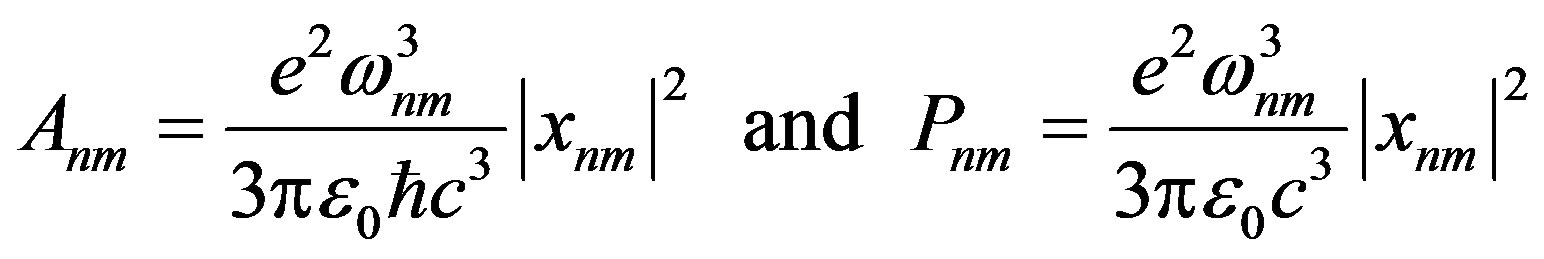 . (2.72)
. (2.72)
Among the key equations of Heisenberg’s famous paper that started modern mechanics were a multiplication rule for quantum-theoretical quantities and a quantum condition that was identical with the Thomas-Kuhn sum rule. Within a few weeks after reading Heisenberg’s paper, Born interpreted the multiplication rule as the rule for matrix multiplication and the quantum condition as the statement that each of the diagonal elements of the matrix 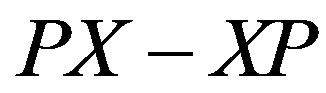 is equal to
is equal to 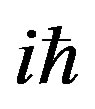 [16]. The reader should well take in mind that Clifford abstract entities should not be confused with matrices since by this way we have only their isomorphic representation, however the initial Born interpretation represents the initial step to conceive a bare bone skeleton of quantum mechanics realized by Clifford algebra. The further step, realized by Pauli [17], was the analysis of the Hydrogen atom by Pauli by using the well known Lorentz-Runge Lentz vector [18,19].
[16]. The reader should well take in mind that Clifford abstract entities should not be confused with matrices since by this way we have only their isomorphic representation, however the initial Born interpretation represents the initial step to conceive a bare bone skeleton of quantum mechanics realized by Clifford algebra. The further step, realized by Pauli [17], was the analysis of the Hydrogen atom by Pauli by using the well known Lorentz-Runge Lentz vector [18,19].
In substance he used three matrices
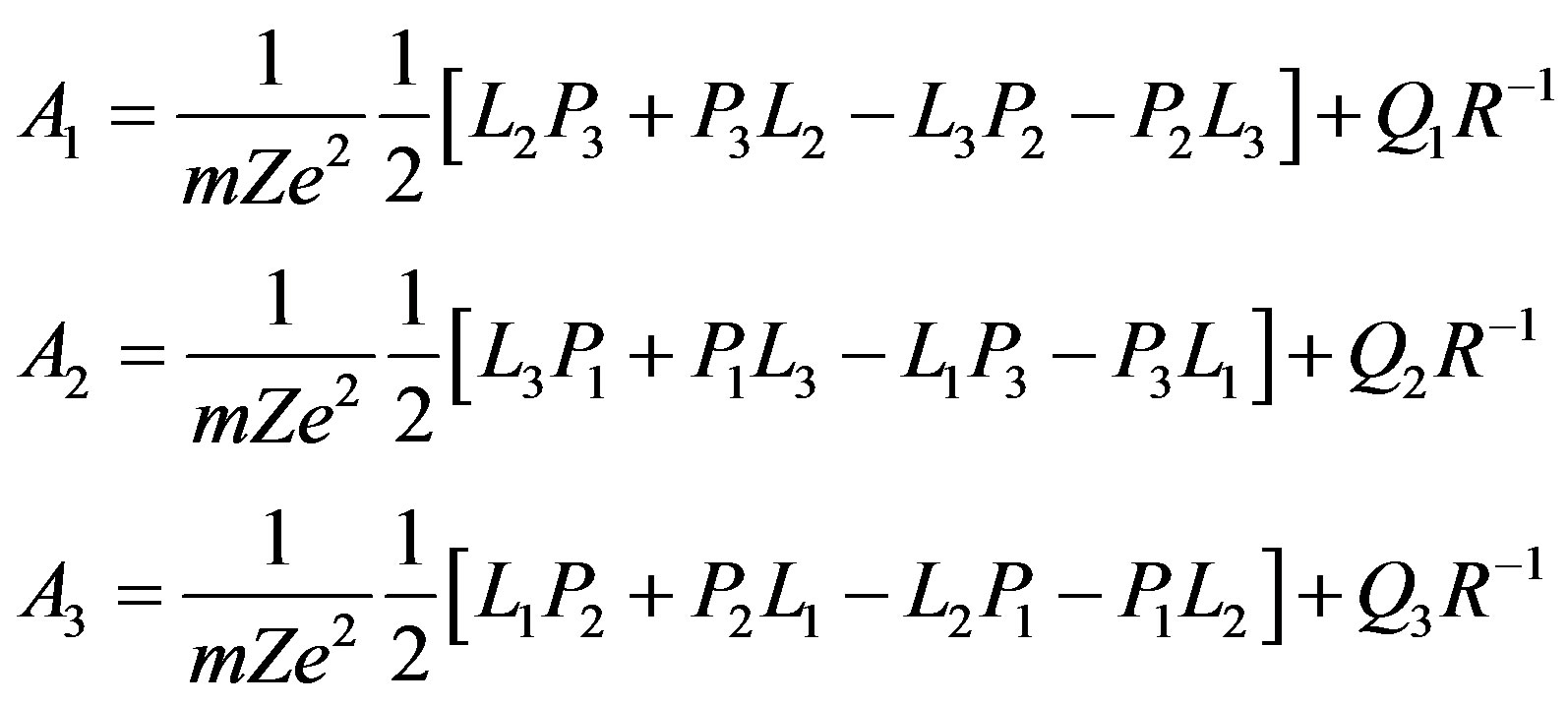 (2.73)
(2.73)
with
 (2.74)
(2.74)
They satisfy the following basic properties:

and
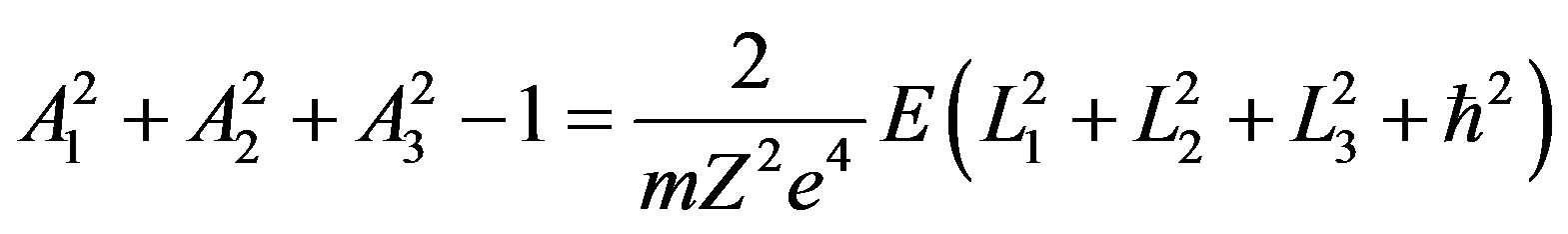 (2.75)
(2.75)
where it results that
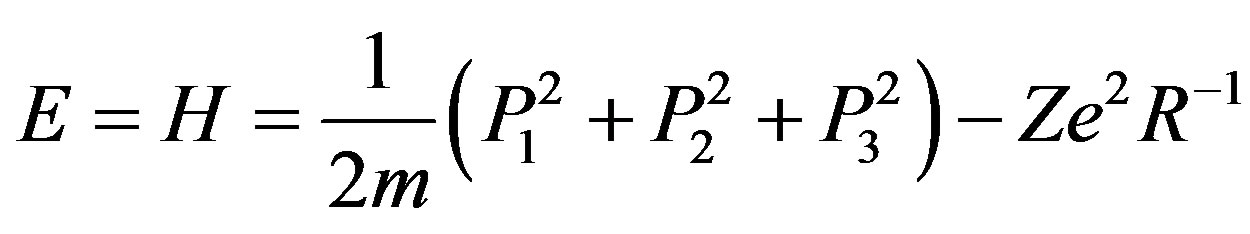 (2.76)
(2.76)
It is trivial to acknowledge the basic meaning of .
.
Still we find that the following relations hold.
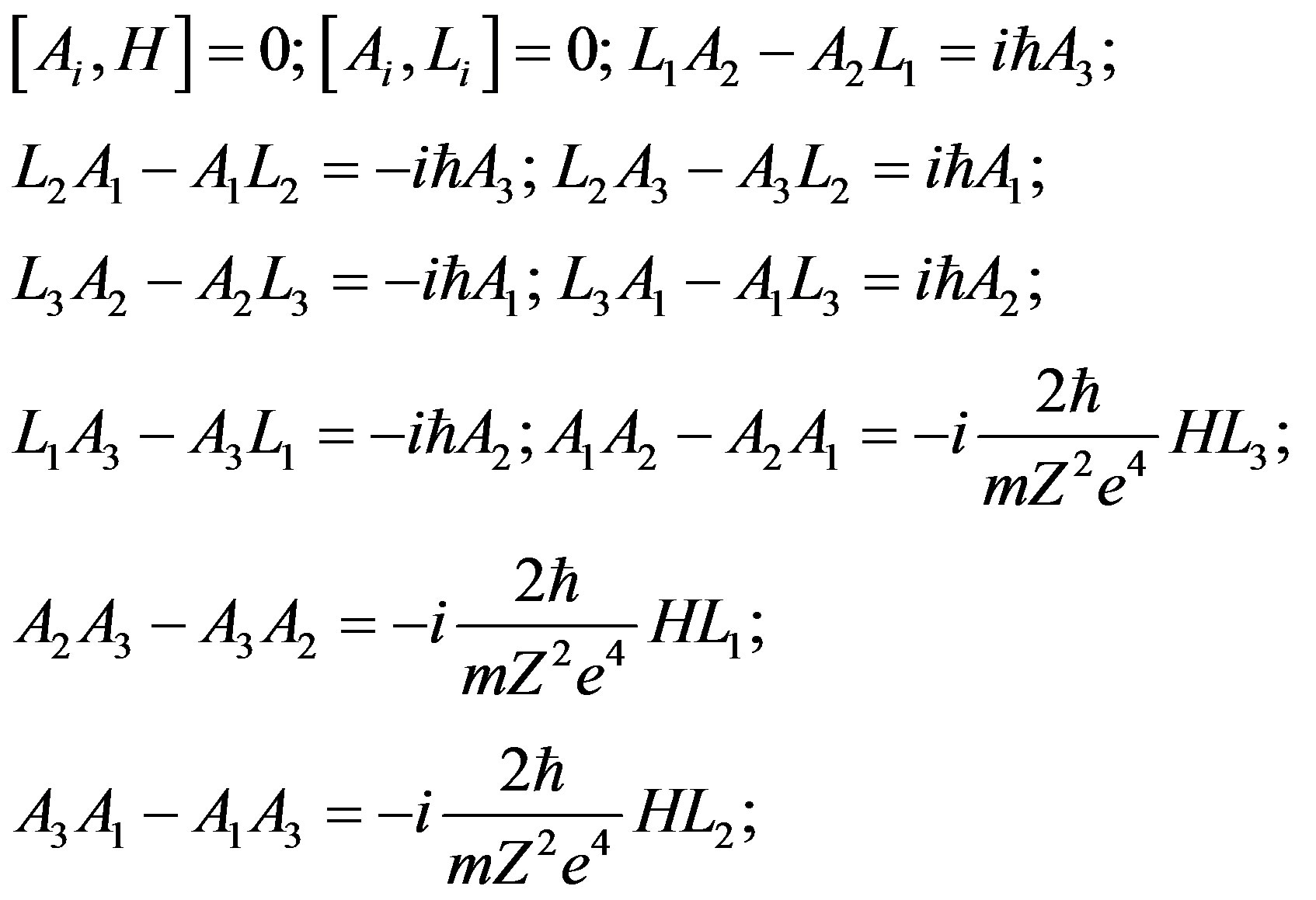 (2.77)
(2.77)
Let us attempt to write Clifford basic elements in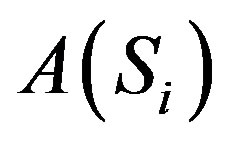 .
.
Consider the following elements
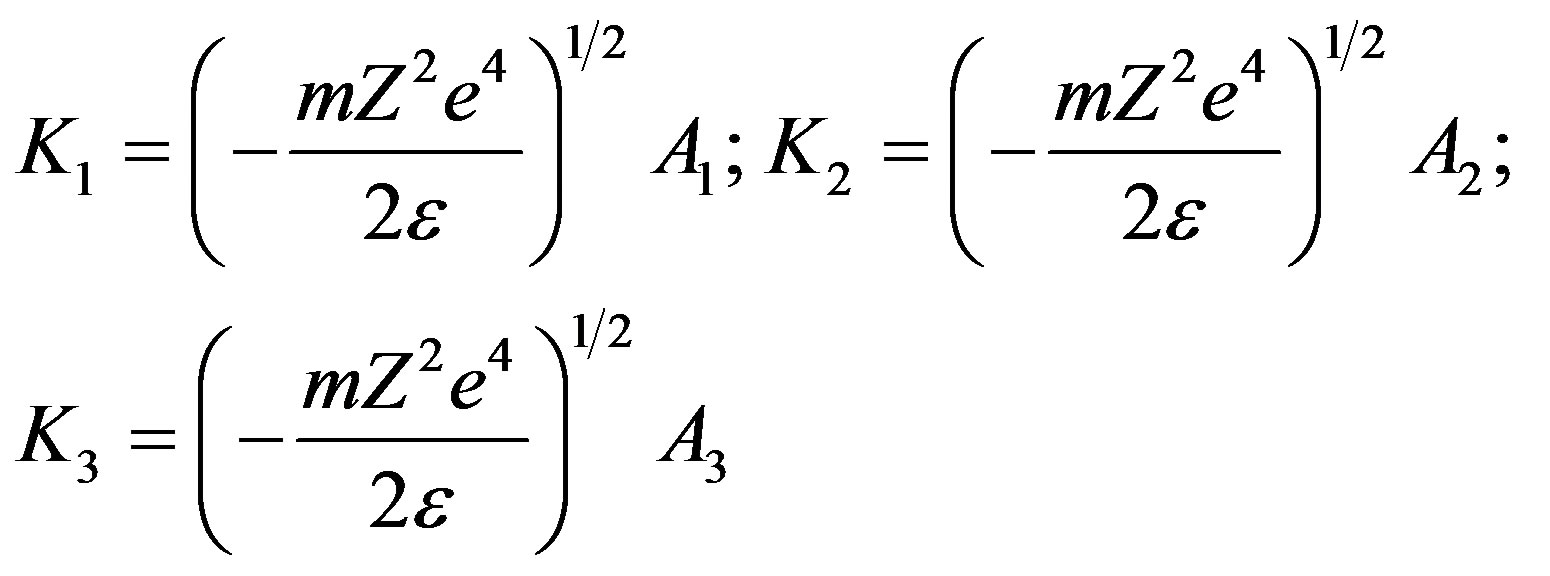 (2.78)
(2.78)
We will obtain that
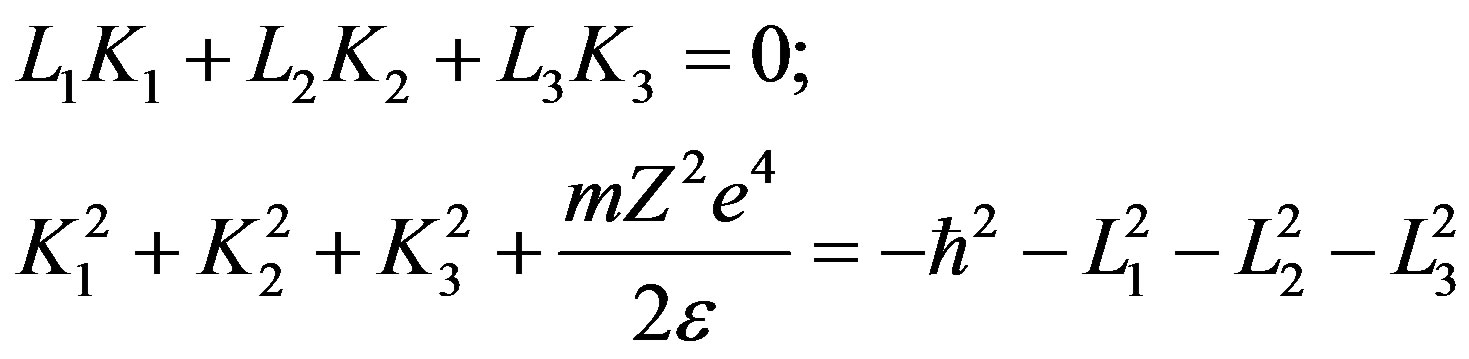
and finally it results that
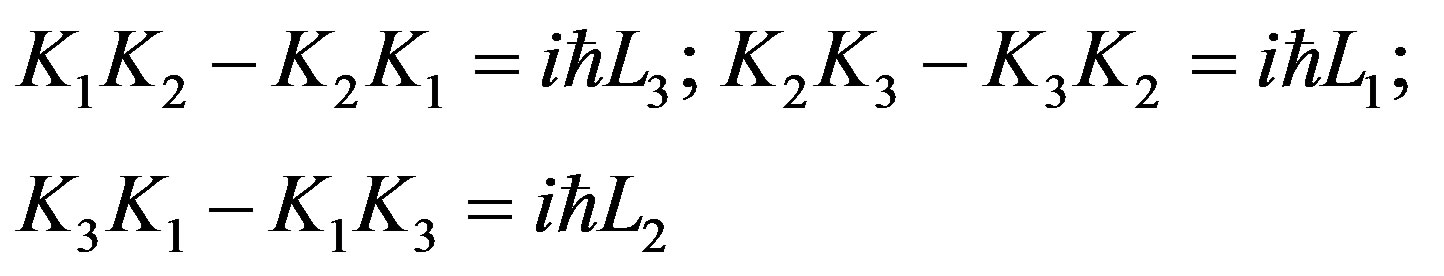 (2.79a)
(2.79a)
Let us introduce still the following basic elements
 (2.79b)
(2.79b)
We have that
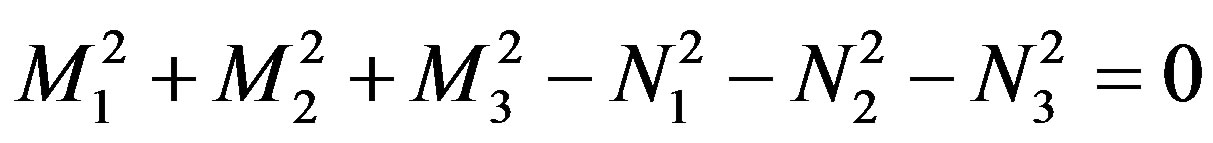 (2.80)
(2.80)
The second important property is that
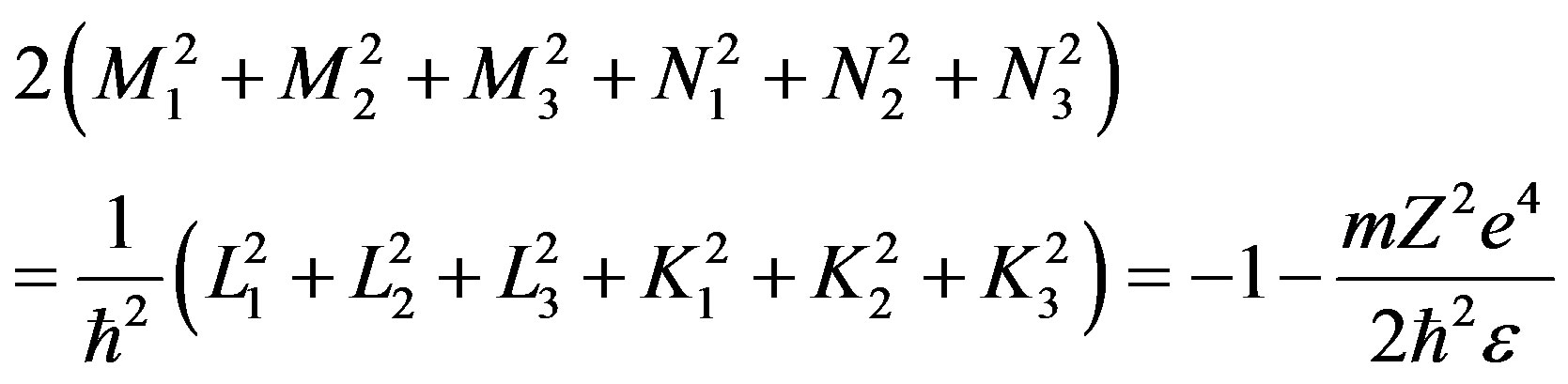 (2.81)
(2.81)
The basic property that we need to be sure to be in the Clifford algebraic structure 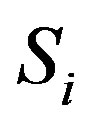 is that we now have
is that we now have
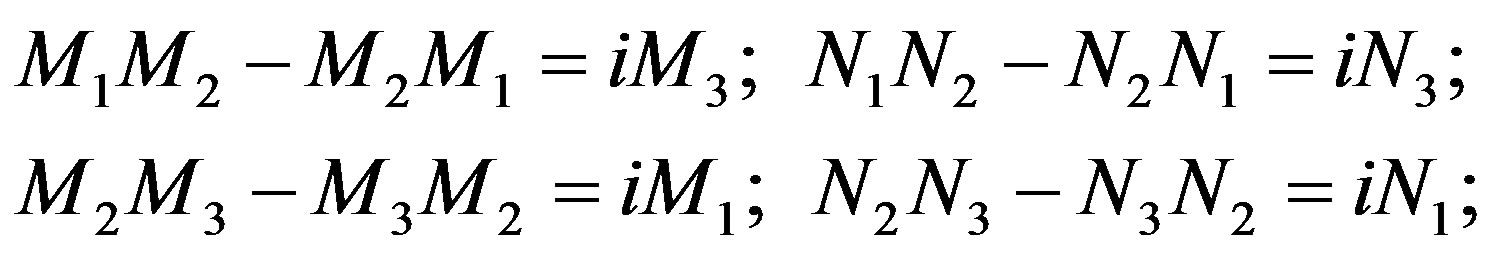 (2.82)
(2.82)
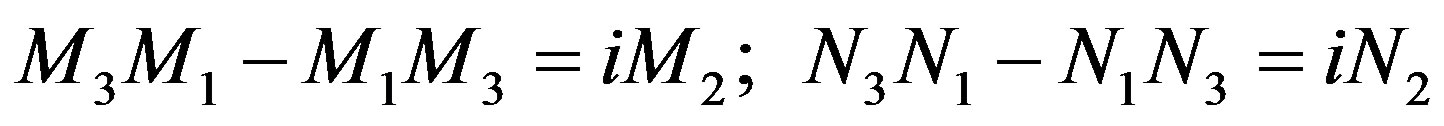 (2.83)
(2.83)
as we obtained previously in (2.68) and in (2.69).
We have now given proof that we are in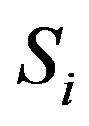 .
.
We have
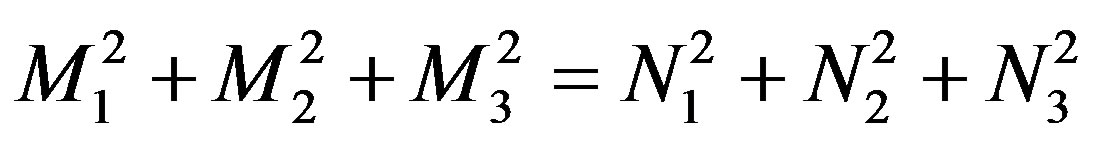 (2.84)
(2.84)
and
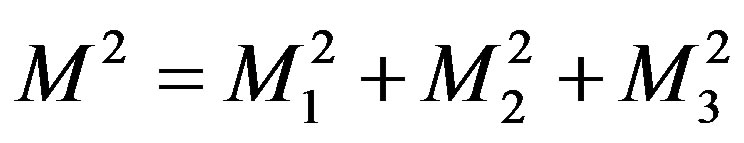 . (2.85)
. (2.85)
We may again realize the Clifford algebraic elements
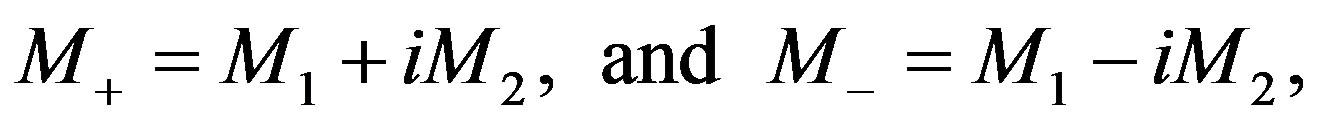 (2.86)
(2.86)
and
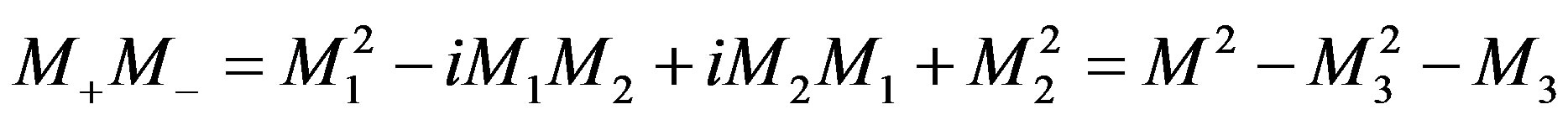 (2.87)
(2.87)
and
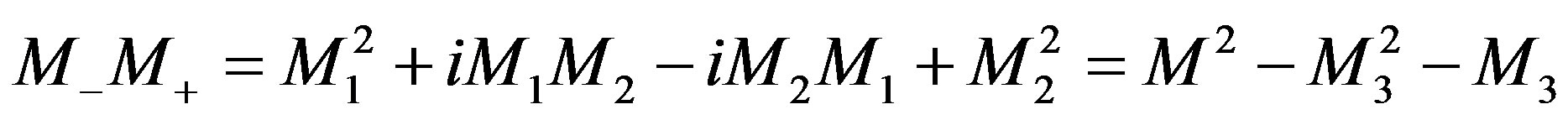
with
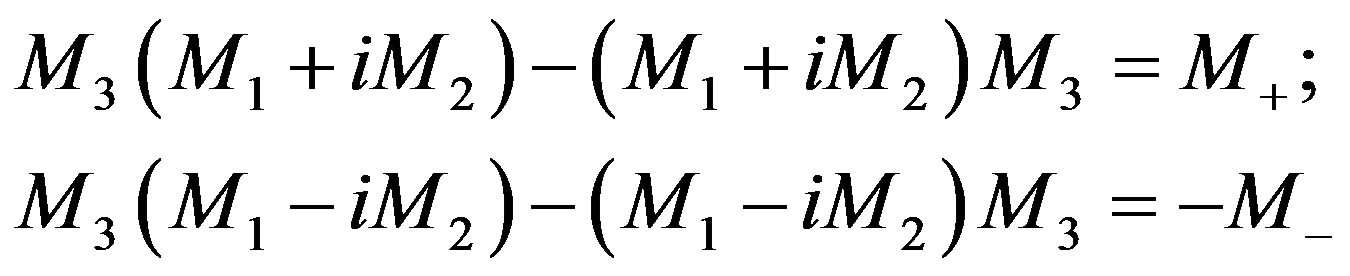 (2.88)
(2.88)
Since we have found that
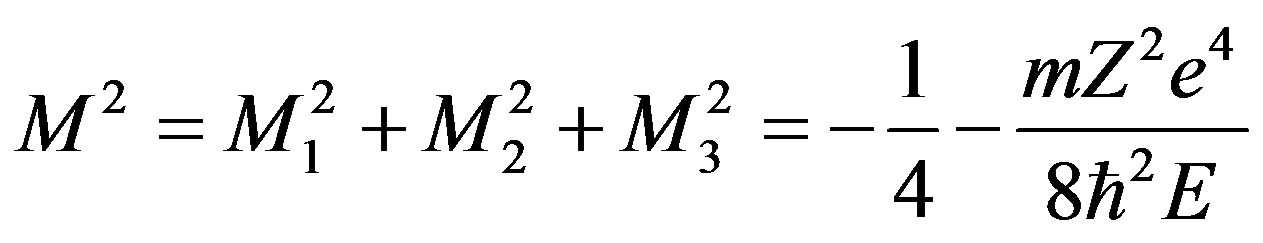 (2.89)
(2.89)
under the condition  < 0, we write that
< 0, we write that
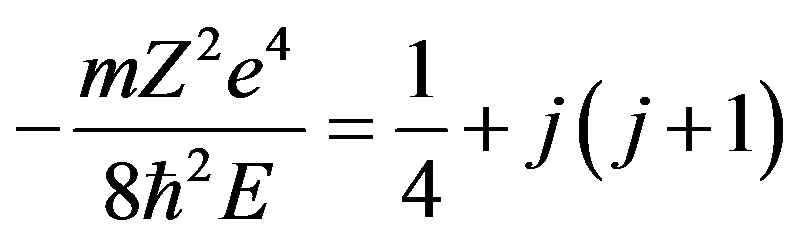 (2.90)
(2.90)
or
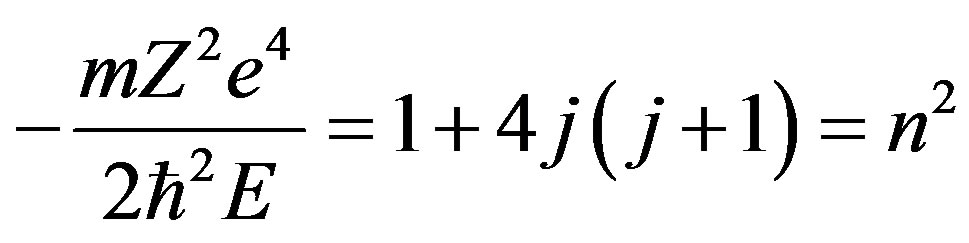 (2.91)
(2.91)
with .
.
In conclusion, we have that
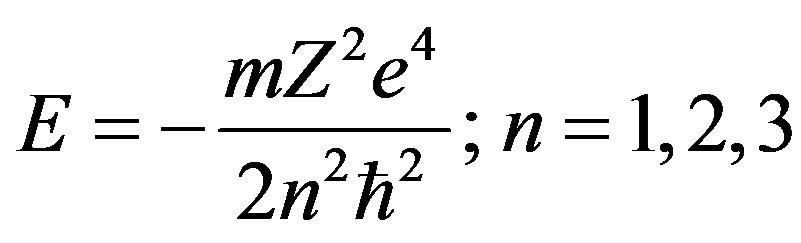 (2.92)
(2.92)
that is just the usual formula of the energy levels for the hydrogen atom as it is obtained in the standard case of the usual quantum mechanics.
It is instructive to observe that the (2.92) arises from the (2.89) that we have obtained by using the (2.82), the (2.83), and, in particular the (2.88). Again idempotent elements are contained in such basic formulation since, looking at the new basic Clifford scheme given in the (2.69) we have expressions as
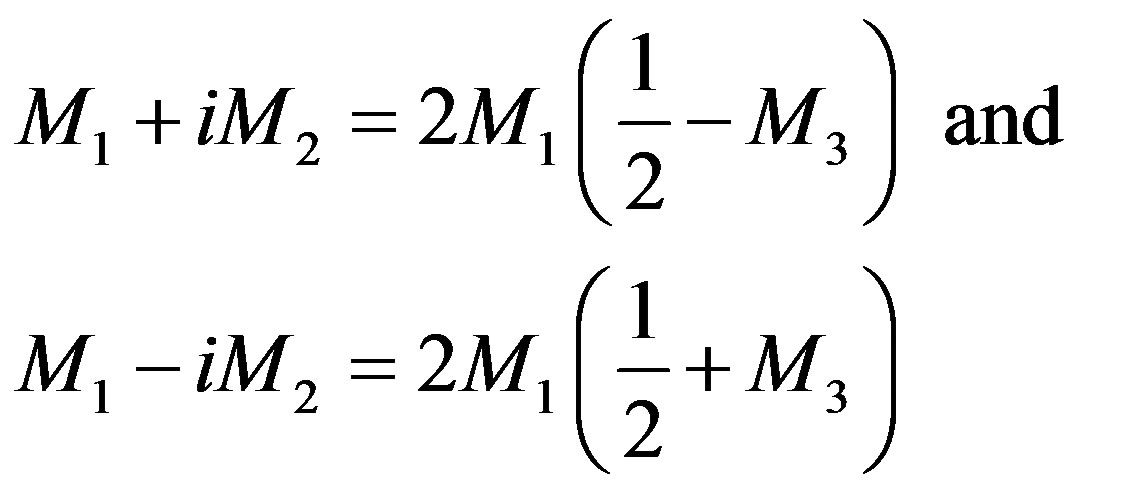 (2.93)
(2.93)
where
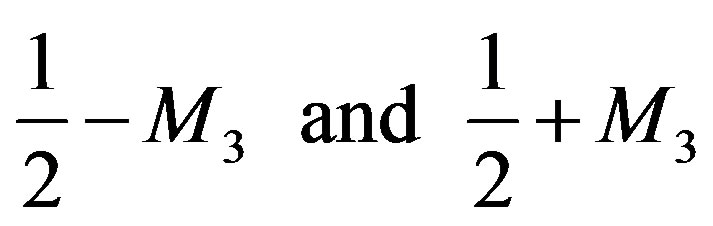 (2.94)
(2.94)
are still idempotent elements according to the (2.69).
3. CONCLUSIONS
The conclusion seems thus unquestionable.
We have derived quantization as general approach to quantum systems. After we have discussed the general case of the classical quantum harmonic oscillator. Soon after we have also discussed the case of the angular momentum. Subsequently we have given a rapid look at the initial quantization procedure as it was formulated initially by Heisenberg, Born, Pauli, Jordan. Still, using the Lorentz-Runge Lentz vector that of course was used also by Pauli, we have performed the analysis of hydrogen atom energy levels. According to standard formulation of quantum mechanics, we have covered a rather large spectrum of interest in this discipline. Always we have found the same result. Idempotent elements are involved. Since, as previously said, idempotent elements are representative of logical statements and thus of cognition and semantics, we conclude that in the basic foundation of our quantized basic reality ab initio there are elements of existence defined, not in terms of some hazy metaphysical concept of existence, but in the sense that existence, related to the cognitive act, is represented by abstract entities of the Clifford algebra, and it contains only two possibilities: existence or non-existence. A pure dichotomic cognitive variable structured ab initio in the inner architecture of our reality. There is ab initio in quantum reality a variable, we could call it “the factor of knowledge and existence” that travels with more traditional physical variables that identify matter per se and that we are accustomed to use in the traditional approach to reality that we formulate in classical physics. There are stages of our reality in which we no more may separate matter per se from the cognition and the principle of existence that we have to attribute to it.
There is still a question that remains to be explained in such novel scheme of quantum reality that we delineate.
Where is that quantum mechanics prospects so innovative peculiarities that of course are totally missing in traditional classical physics?
Let us take a step back. J. von Neumann [2] showed that projection operators , satisfying as it is well known that
, satisfying as it is well known that , and quantum density matrices can be interpreted as logical statements.
, and quantum density matrices can be interpreted as logical statements.
Let us consider a quantum system  and its quantum observable
and its quantum observable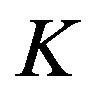 .
. 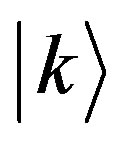 is a state vector for the quantum state in which the observable
is a state vector for the quantum state in which the observable 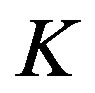 is equal to
is equal to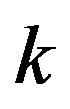 . The density matrix
. The density matrix 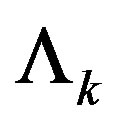 with
with
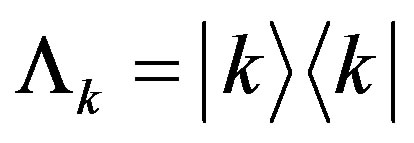 represents the logical statement
represents the logical statement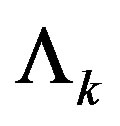 . It says “
. It says “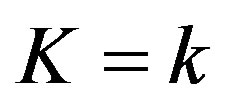 ”. All statements corresponding to mutually commutative observables, constitute a classical logic of propositions where each statement or proposition is represented by its matrix.
”. All statements corresponding to mutually commutative observables, constitute a classical logic of propositions where each statement or proposition is represented by its matrix.
This is of course the basic argument that was developed from Y. F. Orlov just in 1993 [13]. The conclusion is what we have previously evidenced by using Clifford algebra. It is that the main quantum phenomena as quantization, indeterminism, quantum interference can be connected at the basic foundations of the theory with a purely logic basis, and thus with cognition and by it also with an intrinsic principle of existence. The only peculiar nature is that in this elaboration, the statements are represented by projectors, that is to say, as algebraic counterpart, as idempotent elements that of course are isomorphic to Hermitean matrices.
Generally speaking, let  be an observable with a set of possible numerical values (quantum numbers, eigenvalues ),
be an observable with a set of possible numerical values (quantum numbers, eigenvalues ),  , and let the connected physical system be in state
, and let the connected physical system be in state . The logical statement
. The logical statement  is
is
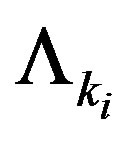 : “The system is in state
: “The system is in state
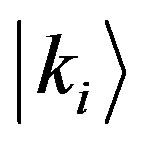 , (2.95)
, (2.95)
that means that
 , (2.96)
, (2.96)
It describes the real situation in this case and therefore it is true.
As it is well known, generalizing we arrive to write the most general relation of quantum mechanics
 (2.97)
(2.97)
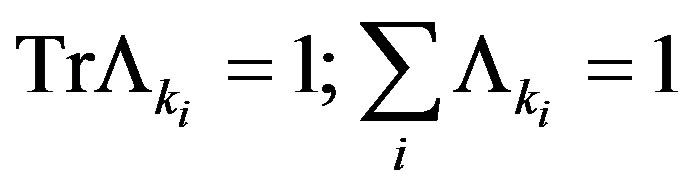 (2.98)
(2.98)
In the (2.97) 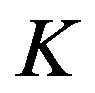 is an operator-observable, connected directly to observable features of matter.
is an operator-observable, connected directly to observable features of matter.  are instead logic statements, thus connected to cognition. The (2.97) clearly explains that such two basic features, matter from one hand and cognition from the other hand, are indissolubly connected from its starting in the theory. Matter cannot be conceived per se but in relation to the cognition that it is possible to have about it. Logic statements, i.e. cognitive elements
are instead logic statements, thus connected to cognition. The (2.97) clearly explains that such two basic features, matter from one hand and cognition from the other hand, are indissolubly connected from its starting in the theory. Matter cannot be conceived per se but in relation to the cognition that it is possible to have about it. Logic statements, i.e. cognitive elements 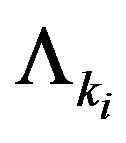 are quantum observables themselves, nonlocal by nature, variables themselves in the dynamics of our reality and commuting with the corresponding quantum observables. The truths of logical statements about numerical values of quantum observables are quantum observables themselves and are represented in quantum mechanics by density matrices of pure states. In this manner a new framework of quantum reality arises in which ab initio information, cognition and principle of existence are structured in it. Matter does no go on by only in its dynamics but it is constantly coupled to an actual principle of existence and to cognition.
are quantum observables themselves, nonlocal by nature, variables themselves in the dynamics of our reality and commuting with the corresponding quantum observables. The truths of logical statements about numerical values of quantum observables are quantum observables themselves and are represented in quantum mechanics by density matrices of pure states. In this manner a new framework of quantum reality arises in which ab initio information, cognition and principle of existence are structured in it. Matter does no go on by only in its dynamics but it is constantly coupled to an actual principle of existence and to cognition.
We have thus two new principles that in our view point delineate new possibilities linking matter to cognitive primitive processes.
The first principle is that logic, cognition, semantic acts are intrinsically structured in the basic scheme of our reality as it relates quantum mechanics.
The second important principle is that in this scheme cognition, here intended as logic statement, does not remain an abstract entity as we are accustomed to admit about cognitive entities, but becomes a quantum observable itself as explained previously.
We are thus in presence of a new approach that has definite implications also for cognitive sciences. Here the starting point is a new physical model in which cognition, also if intended as primitive cognitive entity, is contained ab initio as basic founding principle in the dynamics of reality. In fact in our model we have spoken about a “factor of knowledge” that in quantum reality goes on travelling with the dynamics of the matter.
Have we probing evidences in psychology that could support such view point?
Let us start with some simple example, considering in particular some important papers that years ago were discussed by R. F. Bordley [20].
There is a basic and well known experiment in quantum mechanics. Electrons are produced from a source and move toward a wall with two slits. Let us admit that we install a device that runs as detection screen. It is posed behind the wall and in this manner we may record whether or not the electron hits at a point 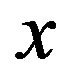 along the wall.
along the wall.
Let us examine different experimental cases. Close the first slit, the slit 1. The probability 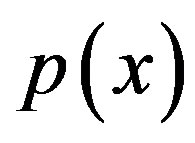 with which the electron hits different positions
with which the electron hits different positions 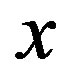 is given by a shaped distribution with the maximum at
is given by a shaped distribution with the maximum at 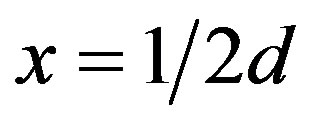 that is the position on the screen directly from slit 2.
that is the position on the screen directly from slit 2.
Now we open the slit 2 and close the slit 1. than 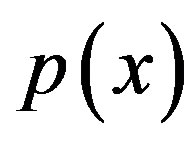 has a shaped distribution with maximum at the point
has a shaped distribution with maximum at the point .We call
.We call  the probability the particle hits pint
the probability the particle hits pint  when slit 1 is closed. It went through the slit 2. Similarly we call
when slit 1 is closed. It went through the slit 2. Similarly we call 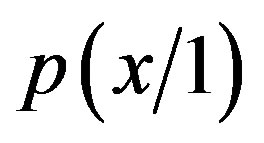 the probability the particle hits pint
the probability the particle hits pint 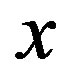 when slit 2 is closed.
when slit 2 is closed.
Now we open both the slits. The probability distribution 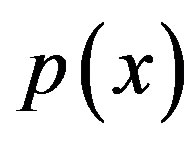 becomes with a maximum centred at
becomes with a maximum centred at 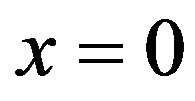 and it has the well known superimposed interference fringes that we well know. Call this probability distribution for two open slits with
and it has the well known superimposed interference fringes that we well know. Call this probability distribution for two open slits with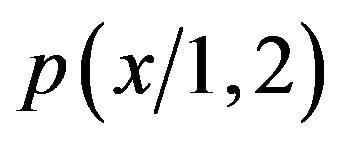 . This is the probability the particle reaches
. This is the probability the particle reaches 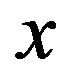 given it can travel through slit 1 or slit 2.
given it can travel through slit 1 or slit 2.
It is also known that we expect some relation among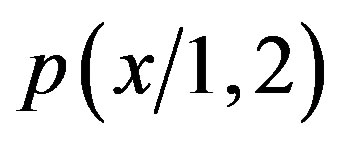 ,
, 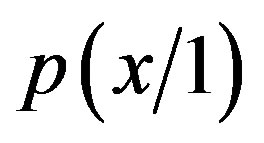 , and
, and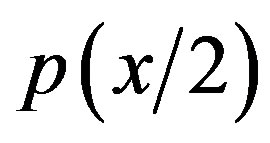 .
.
In fact, if we use the classical theory of probability we have that
 . (2.99)
. (2.99)
As correctly outlined from Bordley where is it the error that we perform at this stage of the usual discussions?
The error is that we assume the following relations to hold:
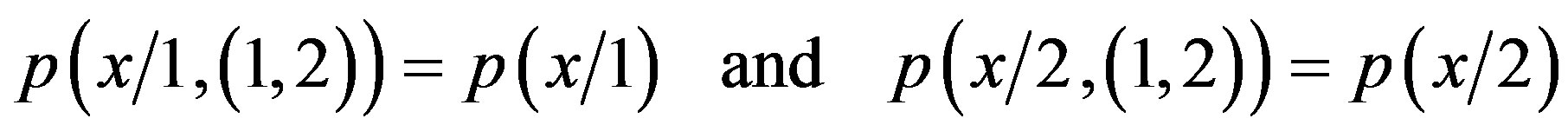 (2.100)
(2.100)
This is the crucial error that we commit.
The (2.100) are in evident violation of the whole model that we have delineated in the present paper.
We cannot admit that
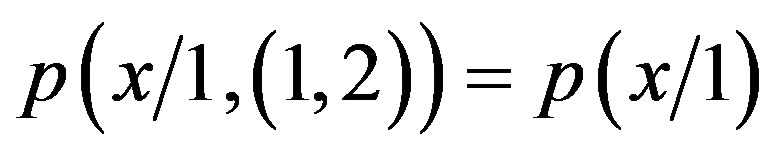 (2.101)
(2.101)
and we cannot admit that
 (2.102)
(2.102)
and the basic reason is that the above mentioned equations, on the basis of the arguments previously outlined, contain a basic difference. This difference is the “knowledge factor” (thus the logic statement and thus the primitive cognition act) that characterizes
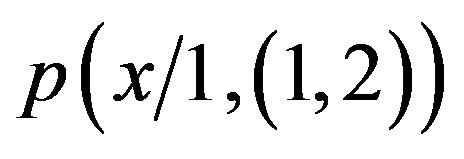 respect to
respect to 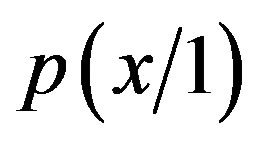 and
and  respect to
respect to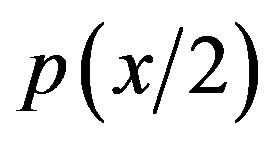 . Relating available information, that is knowledge and thus cognition features, the two relations in the (2.101) and in the (2.102) cannot be admitted at some stages of our reality.
. Relating available information, that is knowledge and thus cognition features, the two relations in the (2.101) and in the (2.102) cannot be admitted at some stages of our reality.
The basic reason is that we cannot ignore the cognitive feature that, as a quantum variables, is structured ab initio in our reality so that the two experimental conditions responding respectively to 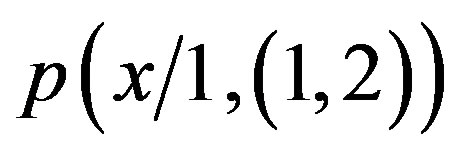 and to
and to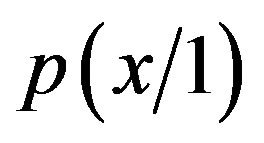 , and, respectively, to
, and, respectively, to 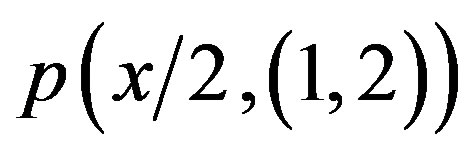 and
and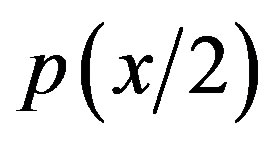 , are totally different.
, are totally different.
This evidence concludes in some manner our exposition. It remains only a feature to be discussed.
Let us see the problem. It is as following. Speaking now at a general level involving directly human cognition and decisions, have we some experimental evidence that at such cognitive level we have an human behaviour that confirms such our model? The answer to such question is affirmative.
We intend to recall here the words of R. F. Bordley that in our opinion wrote an excellent paper [21] in 1997 taking the focus of the question.
First of all we have to observe about a possible analogy. He says that just as physicists usually consider physical systems undergoing trajectories for which the action is an extremum, also scholars in the psychology or social sciences retain that human beings make those choices that lead to consequences having the highest possible value or action. The action associated with an experiment that has 50% chance of giving apples and 50% of giving pears, is equal to the average of the action associated with apples and the action associated with pears. However, experiments in cognitive psychology have evidenced that subjects appear inconsistent with this approach in the sense that they appear to perform decisions that cannot be modelled with any action function. Generally speaking, if in a psychological gamble, the action associated with the pay off 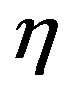 is
is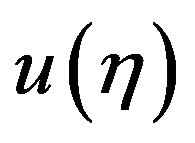 , theory states that the subject choose the pay off
, theory states that the subject choose the pay off  for which
for which  is the smallest. Theory makes predictions also in the case in which one cannot be guaranteed of getting a given pay off. Here we introduce the probability
is the smallest. Theory makes predictions also in the case in which one cannot be guaranteed of getting a given pay off. Here we introduce the probability 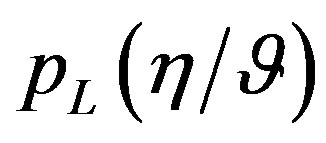 of getting pay off
of getting pay off 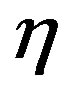 given the occurrence of the event
given the occurrence of the event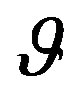 .
.  states for the offered experiment. If the probability of state
states for the offered experiment. If the probability of state 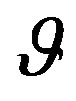 is called
is called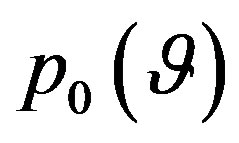 , the assigned action is
, the assigned action is
 (2.103)
(2.103)
where 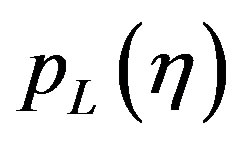 is usually defined as
is usually defined as
 (2.104)
(2.104)
Here is the mandatory point that relates the thesis of our paper.
We have here the following situation. 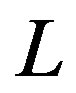 represents the decision maker’s state of knowledge. The (2.104) states that a compound experiment in which first is resolved the uncertainty of the decision maker about an intermediate outcome
represents the decision maker’s state of knowledge. The (2.104) states that a compound experiment in which first is resolved the uncertainty of the decision maker about an intermediate outcome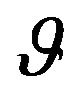 ,
,  , and then, contingent on the intermediate outcome
, and then, contingent on the intermediate outcome , is resolved the uncertainty of the decision maker on
, is resolved the uncertainty of the decision maker on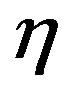 ,
,  , is reducible to a simple experiment in which directly it is resolved the uncertainty of the decision maker about
, is reducible to a simple experiment in which directly it is resolved the uncertainty of the decision maker about .
.
The central question is that a vast number of literature [22] evidences that the way we actually choose among experiments, does not minimize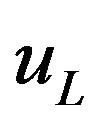 . We know that many theories have attempted to overcome such basic difficulties as Kahneman-Tversky [23], Hogarth-Einborn [24], Chew approach [25], Fishburn model [26].
. We know that many theories have attempted to overcome such basic difficulties as Kahneman-Tversky [23], Hogarth-Einborn [24], Chew approach [25], Fishburn model [26].
Segal has evidenced that the basic violation is contained in the (2.104) [27].
If we denote the information the subject as 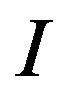 prior to receive the experiment, we have
prior to receive the experiment, we have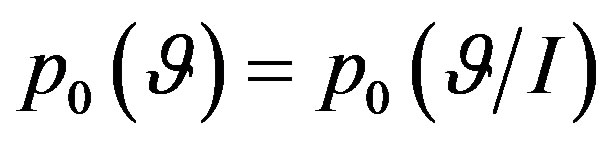 . Since the decision maker becomes aware of the experiment, the starting background information
. Since the decision maker becomes aware of the experiment, the starting background information 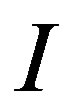 changes, arriving to the new condition
changes, arriving to the new condition . In this manner
. In this manner
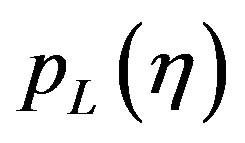 becomes
becomes 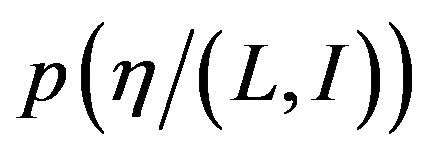 and
and  becomes
becomes .
.
In conclusion, “the factor knowledge” becomes fundamental and unavoidable in cognition of human beings just as it was previously outlined by us in (2.99), in (2.100), in (2.101 ) and (2.102).
To be clear. In human cognition we cannot have
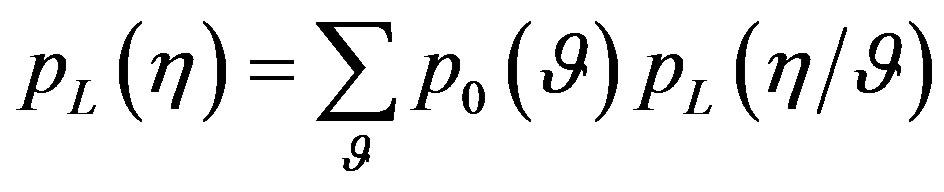 (2.105)
(2.105)
but it is necessarily
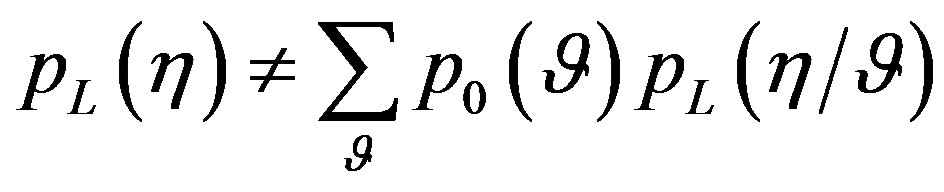 (2.106)
(2.106)
exactly as we find in the present formulation of our theory that the (2.99) no more holds if we claim to insert in it the (2.100).
Of course in the past years we submitted the (2.106) to a number of experimental verification and confirmation at human perceptive-cognitive level [28-50]. Always we found confirmation. We do not discuss in detail such experiments here for brevity but we suggest the reader to examine the results that are reported by us in the quoted references. Reassuming, we may say that we investigated at perceptive-cognitive level by using ambiguous figures. Still we examined the case of semantic conflict by using the well known Stroop effect. Still we considered the case of so called cognitive anomalies by using conjunction fallacy. We also examined experimental situations at cognitive level to demonstrate Bell’s inequality violation in mental states. All such results give experimental and clinical evidence supporting the theory and also indicate a possible way for future applications in neuropsychology. They have the advantage to be now based on a direct and robust theoretical formulation. Finally, we have to outline that the matter to investigate cognitive processes by consideration of quantum mechanics has represented recently also the direct interest of many authors. We invite the reader to take in consideration the quoted references given in [28-50] and the book of A. Khrennikov [51] that gives an extensive list of the contributions given from the different authors.
REFERENCES
- Bell, J.S. (1964) On the Einstein-Podolsky-Rosen paradox. Physics, 1, 195-200.
- Von Neumann, J. (1932) Mathematische grundlagen der quantenmechanik. Springer-Verlag, Berlin.
- Dirac, P.A.M. (1977) History of twentieth century of physics. Weiner Ac. Press, New York.
- Dirac, P.A.M. (1971) The development of quantum mechanics. Gordon and Breach, New York.
- Conte, E. (2010) A proof of Von Neumann’s postulate in quantum mechanics. In: Quantum Theory Reconsideration of Foundations 5, American Institute of Physics, New York, 201-205.
- Conte, E. (2010) A reformulation of von Neumann’s postulates on quantum measurement by using two theorems in Clifford algebra. International Journal of Theoretical Physics, 49, 587-614. doi:10.1007/s10773-009-0239-z
- Stapp, H.P. (2006) Quantum interactive dualism: An alternative to materialism. www-physics.lbl.gov/~stapp/QID.pdf
- Conte, E. (2011) An investigation on the basic conceptual foundations of quantum mechanics by using the Clifford algebra. Advanced Studies in Theoretical Physics, 5, 485- 544.
- Conte, E. (2011) On the logical origins of quantum mechanics demonstrated by using Clifford Algebra: A proof that quantum interference arises in a Clifford algebraic formulation of quantum mechanics. Electronic Journal of Theoretical Physics, 8, 109-126.
- Conte, E. (2011) On the logical origins of quantum mechanics demonstrated by using Clifford algebra. NeuroQuantology, 9, 231-242.
- Conte, E. (2012) What is the reason to use Clifford algebra in quantum cognition? Part I: “It from qubit” on the possibility that the amino acids can discern between two quantum spin states. NeuroQuantology, 10, 561-565.
- Conte, E., Todarello, O., Federici, A., Vitiello, F., Lopane, M. and Khrennikov, A.Y. (2004) A preliminary evidence of quantum like behaviour in measurements of mental states. In: Quantum Theory: Reconsideration of Foundations 2, Vaxjo University Press, Vaxjo, 679-702.
- Orlov, Y.F. (1994) The logical origins of quantum mechanics. Annals of Physics, 234, 245-259. doi:10.1006/aphy.1994.1081
- Eddington, A.S. (1946) Fundamental theory. Cambridge.
- Bohm, D.J., Davies, P.G. and Hiley, B.J. (1982) Algebraic quantum mechanics and pregeometry. Unpublished, 1982.
- Mehra, J. and Rechenberg, H. (1982) The historical development of quantum theory. Sprinegr-Verlag, New York. doi:10.1007/978-1-4612-5783-7
- Pauli, W. (1926) Über das wasserstoffspektrum vom standpunkt der neuen quantenmechanik. Zeitschrift für Physik, 36, 336-363. doi:10.1007/BF01450175
- Laplace, P.S. (1799) Traité de mécanique celeste, tome I, premiere partie, livre II 165, GAUTFUER-VII.LAKS, Paris.
- Lenz, W. (1924) Über den bewegungsverlauf und quantenzustände der gestörten keplerbewegung. Zeitschrift für Physik, 24, 197-207. doi:10.1007/BF01327245
- Bordley, R.F. (1983) Modeling quantum behavior with standard (nonquantum) probability theory. Journal of Mathematical Physics, 24, 2411-2421. doi:10.1063/1.525622
- Bordley, R.F. (1997) Experiment-dependent probabilities in quantum-mechanics and psychology. Physics Essays, 10, 401-406. doi:10.4006/1.3036426
- Kanheman, D., Slovic, P. and Tversky, A. (1982) Judgement under uncertainty: Heuristics and biases. Cambridge University Press, Cambridge. doi:10.1017/CBO9780511809477
- Kanheman, D. and Tversky, A. (1979) Prospect theory: An analysis of decisions under risk. Econometrica, 47, 263-291. doi:10.2307/1914185
- Hogarth, H. and Einborn, H. (1990) Venture theory: A model of decision weights. Management Science, 36, 780- 803. doi:10.1287/mnsc.36.7.780
- Chew, S. (1983) A generalisation of the quasilinear mean with applications to the ... and decision theory resolving the Allais paradox. Econometrica, 51, 1065-1092. doi:10.2307/1912052
- Fishburn, P. (1988) Non linear preference and utility theory. John Hopkins University Press, Baltimore.
- Segal, U. (1988) Does the preference reversal phenomenon necessarily contradict the independence axiom? American Economic Review, 78, 233-236.
- Conte, E. (2011) On the logical origins of quantum mechanics demonstrated by using Clifford algebra: A proof that quantum interference arises in a Clifford algebraic formulation of quantum mechanics. Electronic Journal of Theoretical Physics, 8, 109-126.
- Conte, E. (2011) On the logical origins of quantum mechanics demonstrated by using Clifford algebra. Neuroquantology, 9, 231-242.
- Conte, E. (2012) What is the reason to use Clifford algebra in quantum cognition? Part I: “It from qubit” on the possibility that the amino acids can discern between two quantum spin states. Neuroquantology, 10, 561-565.
- Conte, E., Todarello, O., Federici, A., Santacroce, N., Laterza, V. and Khrennikov, A.Y. (2012) May we verify non-existing dispersion free ensembles by application of quantum mechanics in experiments at perceptive and cognitive level? Neuroquantology, 10, 14-19.
- Conte, E. (2012) Advances in application of quantum mechanics in neuroscience and psychology: A Clifford algebraic approach. Nova Science Publishers, New York.
- Conte, E., Santacroce, N. and Federici, A. (2012) A possible quantum model of consciousness interfaced with a non-lipschitz chaotic dynamics of neural activity (Part I) and (Part II). Journal of Consciousness Exploration & Research, 3, 905-936.
- Conte, E., Khrennikov, A.Y., Todarello, O., De Robertis, R., Federici, A. and Zbilut, J.P. (2012) On the possibility that we think in a quantum mechanical manner: An experimental verification of existing quantum interference effects in cognitive anomaly of conjunction fallacy. In: On the Borders of Complexity Cap, Nova Science Publishers, Inc., Hauppauge, 149-163.
- Conte, E., Santacroce, N., Laterza, V., Conte, S., Federici, A. and Todarello, O. (2012) The brain knows more than it admits: A quantum model and its experimental confirmation. Electronic Journal of Theoretical Physics, 9, 72- 110.
- Conte, E., Khrennikov, A.Y., Todarello, O., De Robertis, R., Federici, A. and Zbilut, J.P. (2011) On the possibility that we think in a quantum mechanical manner: An experimental verification of existing quantum interference effects in cognitive anomaly of conjunction fallacy. Chaos and Complexity Letters, 4, 123-136.
- Conte, E. (2010) The possibility that we think in a quantum probabilistic manner. Neuroquantology, 8, 3-47.
- Conte, E., Todarello, O., Laterza, V., Khrennikov, A.Y., Mendolicchio, L. and Federici, A. (2010) A preliminary experimental verification of violation of bell inequality in a quantum model of Jung theory of personality formulated with Clifford algebra. Journal of Consciousness Exploration & Research, 1, 831-849.
- Conte, E. (2009) A brief note on time evolution of quantum wave function and of quantum probabilities during perception and cognition of human subjects. Neuroquantology, 7, 435-448.
- Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A. and Zbilut, J.P. (2009) On the existence of quantum wave function and quantum interference effects in mental states: An experimental confirmation during perception and cognition in humans. Neuroquantology, 7, 204-212.
- Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A., Mendolicchio, L. and Zbilut, J.P. (2009) Mental states follow quantum mechanics during perception and cognition of ambiguous figures. Open Systems & Information Dynamics, 16, 1-17. doi:10.1142/S1230161209000074
- Conte, E., Khrennikov, A.Y., Todarello, O., Federici, A. and Zbilut, J.P. (2008) A preliminary experimental verification on the possibility of bell inequality violation in mental states. Neuroquantology, 6, 214-221.
- Conte, E. (2008) Testing quantum consciousness. Neuroquantology, 6, 126-139.
- Conte, E., Todarello, O., Federici, A., Vitiello, F., Lopane, M., Khrennikov, A.Y. and Zbilut, J.P. (2007) Some remarks on an experiment suggesting quantum-like behavior of cognitive entities and formulation of an abstract quantum mechanical formalism to describe cognitive entity and its dynamics. Chaos, Solitons and Fractals, 31, 1076-1088. doi:10.1016/j.chaos.2005.09.061
- Conte, E., Pierri, G.P., Federici, A., Mendolicchio, L. and Zbilut, J.P. (2006) A model of biological neuron with terminal chaos and quantum-like features. Chaos, Solitons and Fractals, 30, 774-780. doi:10.1016/j.chaos.2005.08.211
- Conte, E., Pierri, G.P., Mendolicchio, L., Khrennikov, A.Y. and Zbilut, J.P. (2006) On some detailed examples of quantum like structures containing quantum potential states in the sphere of biological dynamics. Cornell University Library.
- Conte, E., Khrennikov, A.Y. and Zbilut, J.P. (2006) The transition from ontic potentiality to actualization of states in quantum mechanical approach to reality: The proof of a mathematical theorem to support it. Cornell University Library.
- Conte, E., Todarello, O., Federici, A., Vitiello, F., Lopane, M. and Khrennikov, A.Y. (2004) A preliminary evidence of quantum like behaviour in measurements of mental states. In: Quantum Theory: Reconsideration of Foundations 2, Vaxjo University Press, Vaxjo.
- Conte, E. (2013) What is the reason to use Clifford algebra in quantum cognition? Part II: Information, cognition and the principle of existence are intrinsically structured in the quantum model of reality. NeuroQuantology, 11, 34-46.
- Conte, E. (2013) Are information, cognition and the principle of existence intrinsically structured in the quantum model of reality? Advanced Studies in Theoretical Physics.
- Khrennikov, A. (2010) Ubiquitous quantum structure. Springer, New York. doi:10.1007/978-3-642-05101-2
NOTES
*A preliminary and partial version of the present paper, based on the mathematical and physical foundations, is going to be published on NeuroQuantology and on Advanced Studies in Theoretical Physics.

