Journal of Quantum Information Science
Vol.06 No.01(2016), Article ID:65198,12 pages
10.4236/jqis.2016.61006
The Pancharatnam Phase of a Three-Level Atom Coupled to Two Systems of N-Two Level Atoms
D. A. M. Abo-Kahla
Department of Mathematics, Faculty of Education, Ain Shams University, Cairo, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2016; accepted 25 March 2016; published 30 March 2016
ABSTRACT
In this paper, we present the analytical solution for the model that describes the interaction between a three-level atom and two systems of N-two level atoms. The effects of the quantum numbers and the coupling parameters between spins on the Pancharatnam phase and the atomic inversion, for some special cases of the initial states, are investigated. The comparison between the two effects shows that the analytic results are well consistent.
Keywords:
Pancharatnam Phase, Atomic Inversion, Systems of N-Two Level Atoms

1. Introduction
The use of statistical mechanics is fundamental to the concepts of quantum optics: Light is described in terms of field operators for creation and annihilation of photons [1] - [7] . Features of quantum optics are mainly based on three different types of interaction, namely, field-field, atom-atom, atom-field interaction. Each one of these interactions represents a certain type of physical phenomena [8] - [13] . For example, Hichem Eleuch and Raouf Bennaceur studied the interaction between a three-level system in the lambda configuration with two resonant electromagnetic fields, through which the motion of a pair of solitons propagating through an absorbing three- level system in the lambda configuration was analyzed [14] .
In addition, based on Dicke’s superradiance, Eyob A. Sete et al. studied the collective spontaneous emission from an ensemble of N identical two-level atoms prepared by absorption of a single photon―a.k.a. single photon Dicke superradiance [15] .
In the present communication we are concerned with the type of atom-atom (spin-spin) interaction, the interaction between a three-level atom and two systems of N-two level atoms. The time evolution of dynamical systems has attracted considerable attention over the past several decades because of its various applications. An important aspect in this regard is the quantum phase associated with the evolution of these states in certain circumstances [16] .
In recent years much attention has paid to the quantum phases [17] such as the Pancharatnam phase [18] - [22] and the geometric phase [23] [24] . The concept of geometric phase naturally arises for polarized light in optics. Simple quantum gates using geometric phase have been demonstrated experimentally in the nuclear magnetic resonance setup [25] . In the fifties, Pancharatnam [26] came up with a rigorous prescription for the phase acquired in a completely general evolution of a system. Pancharatnam discovered that when the polarization state of a beam of light was taken around a closed circuit in the state space, namely the Poincar. Sphere, it acquires an extra phase which is equal to half the solid angle subtended by the circuit at the origin of the sphere [27] . In 1956, Pancharatnam [26] studied how the phase of polarized light changed after a cyclic evolution of its polarization [28] . In 1984 Berry addressed a quantum system undergoing a unitary and cyclic evolution under the action of a time-dependent Hamiltonian [29] . The process was supposed to be adiabatic, meaning that the time scale of the system’s evolution was much shorter than the time scale of the changing Hamiltonian [30] .
The Pancharatnam phase or most commonly Berry phase is a phase difference acquired over the course of a cycle when a system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space of the Hamiltonian. The Pancharatnam phase is very important in the propagation of a light beam where its polarization state is changing periodically [18] . Hence, we study the Pancharatnam phase of a three-level atom coupled to two systems of N-two level atoms as an application.
This paper is organized as follows: in section 2, we will describe the Hamiltonian of the system of interest, and obtain the explicit analytical solution of the model describing the interaction between a three-level atom and two systems of N-two level atoms. The case discussed in this paper is considered to be the generalization of the atom-atom interaction, and most of the previous papers which handled this interaction are, for the most part, considered to be a special case of our case. In section 3, different cases are studied to demonstrate the effects due to both the quantum numbers m1, m2 and the coupling parameters between spins λ1, λ2 on the atomic inversion 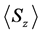 of the model. By analytical calculations in section 4, we examine the influence of the quantum numbers m1, m2 and the coupling parameters between spins λ1, λ2 on the Pancharatnam phase
of the model. By analytical calculations in section 4, we examine the influence of the quantum numbers m1, m2 and the coupling parameters between spins λ1, λ2 on the Pancharatnam phase 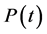 of the model. In section 5, we discuss the second-order correlation function where the examination of the second-order correlation function leads to better understanding for the nonclassical behavior of the system. Finally, section 6 presents the conclusions and an outlook.
of the model. In section 5, we discuss the second-order correlation function where the examination of the second-order correlation function leads to better understanding for the nonclassical behavior of the system. Finally, section 6 presents the conclusions and an outlook.
2. The Model
The Hamiltonian of our model describes the interaction between a three-level atom coupled to two systems of N-two level atoms. In this case the Hamiltonian of the whole system can be written in the form:
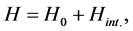 (1)
(1)
where,
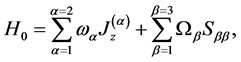 (2)
(2)
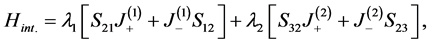 (3)
(3)
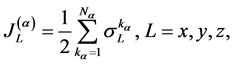 (4)
(4)
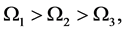 (5)
(5)
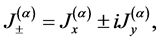 (6)
(6)
where 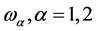 is the strength of the field (the two systems of N-two level atoms). The operators
is the strength of the field (the two systems of N-two level atoms). The operators 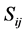 satisfy the commutation relation
satisfy the commutation relation
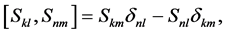 (7)
(7)
while 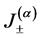 and
and 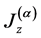 are the collective angular momentum operators for N-two level atoms, which satisfy the relations
are the collective angular momentum operators for N-two level atoms, which satisfy the relations
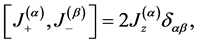 (8)
(8)
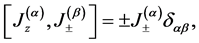 (9)
(9)
and

with the operator 
We define




Let

From Schrödinger equation

we get from Equations (1), (15)



where,




where 
Define

by substituting from Equation (24) in Equations (17)-(19) we get the following equations:



from Figure 1 we set

So, we can write the Equations (25)-(27) as the following:



We solve the Equations (29)-(31) analytically, we get:

where,


Figure 1. Scheme of the interaction between a three-level atom coupled to two systems of N-two level atoms.

similarly


and


So from Equation (24) we get 
As applications to the solution of our case, a three-level atom coupled to two systems of N-two level atoms, we calculate the atomic inversion, the Pancharatnam phase and the correlation functions.
3. The Atomic Inversion
The atomic population inversion
In Figures 2(a)-(c), we consider (Δ = 0, λ1 = λ2 = 1 and j1 = 30, j2 = 20). We investigate the effect of the
quantum numbers m1, m2 on the atomic inversion. In Figure 2(a), the initial state is
inversion (m1 = m2 = 1) has regular and periodic oscillations. It starts from its maximum value, 


(straight line). In Figure 2(b), the initial state is
and periodic oscillations. It starts from its maximum value, 
2(c), the initial state is
It starts from its maximum value, 




Figure 2. The evolution of the atomic inversion as function of the scaled time t. Δ = 0, λ1 = λ2 = 1 and j1 = 30, j2 = 20. The dashed, bold solid, gray solid curves correspond, respectively, to m1 = m2 = 1, 18, 20 Where (a) the initial state is


Figure 3. Figure of the case in which Δ = 0, m1 = m2 = 1, j1 = 30, j2 = 20 and the initial state is
atomic inversion. The atomic inversion has regular and periodic oscillations. It starts from its maximum value, 

4. The Pancharatnam Phase
The total phase both dynamic and geometric phase parts for an arbitrary quantum evolution of a system from a state at t = 0 to a final state at time t. Without invoking the fact that any initial state vector 





In Figure 4, we consider (Δ = 0, λ1 = λ2 = 1 and j1 = 30, j2 = 20 and the initial state is

The Correlation Function
In this section, we discuss the behavior of the second-order correlation function where the examination of the correlation function is usually used to discuss the correlated or uncorrelated behavior from which we can distinguish between classical and nonclassical behavior. The normalized second-order correlation function is defined by [13] [32]

Figure 4. The evolution of the Pancharatnam phase as function of the scaled time t. Δ = 0, λ1 = λ2 = 1 and j1 = 30, j2 = 20 and the initial state is
Figure 5. Figure of the case in which Δ = 0, m1 = m2 = 1, j1 = 30, j2 = 20 and the initial state is
To discuss the behavior of the correlation function, we have to calculate the expectation value of the quantity 

We know that


So


we get from Equations (15) (41)


where


In Figure 6, we consider (Δ = 0, λ1 = λ2 = 1, 

gate the effect of the quantum numbers m1, m2 on the correlation functions 

2 respectively. When






functions








the coupling parameters between spins λ1, λ2 on the correlation functions 





5. Conclusions
In this paper, we analytically solved the model that described the interaction between a three-level atom coupled to two systems of N-two level atoms. We calculated the atomic inversion and the Pancharatnam phase for some special cases of the initial states




Figure 6. The normalized second-order correlation functions 




Figure 7. The normalized second-order correlation functions 




oscillations when the quantum numbers m1, m2 increase, the number of periodic oscillations decreases and the small oscillations disappear gradually. We observe that there is constant interval at the maximum value. It increases remarkably when the coupling parameters between spins λ1, λ2 decrease and the number of periodic oscillations gradually decreases. The Pancharatnam phase has regular and periodic straight lines following the shape of the letter N. We note that there is a regular repeat in the behavior of the Pancharatnam phase. When the quantum numbers m1, m2 increase and the coupling parameters between spins λ1, λ2 decrease, each period of the Pancharatnam phase widens on the time axe and the overall number of periods decreases. Comparing the change of the Pancharatnam phase in Figure 4 and Figure 5, we observe that the effect of the quantum numbers m1, m2 is larger than the effect of the coupling parameters between spins λ1, λ2 in respect to the overall number of periods. Finally, we discuss the second-order correlation function where the examination of the second-order correlation function leads to better understanding for the nonclassical behavior of the system. When the quantum numbers m1, m2 increase the correlated behavior shows remarkably.
The model presented in this paper can further be applied to two-two level atom or two qubits where in this case j = 1. This can make contribution to more understanding and possible applications in the field of quantum optics as well as solid-state physics. In addition, the atom-atom (i.e. spin-spin) interaction is a promising candidate for implementing the quantum computer, which accordingly can be connected vitally to the demonstration of spin dynamics in semiconductor structures [33] .
Acknowledgements
I would like to express my deep gratitude to Professors Abdel-Shafy F. Obada, Mohamed M. A. Ahmed, Department of Mathematics, Faculty of Science, Al-Azhar University and Professor Mahmoud Abdel-Aty, Zewail City of Science and Technology, Giza, Egypt, for their support, care, their useful suggestions, useful discussion and for their continuous help and guidance.
Cite this paper
D. A. M. Abo-Kahla, (2016) The Pancharatnam Phase of a Three-Level Atom Coupled to Two Systems of N-Two Level Atoms. Journal of Quantum Information Science,06,44-55. doi: 10.4236/jqis.2016.61006
References
- 1. Mandel, L. and Wolf, E. (1995) Optical Coherence and Quantum Optics. Cambridge University Press, Cambridge.
http://www.cambridge.org/US/academic/subjects/physics/optics-optoelectronics-and-photonics/optical-coherence-and-quantum-optics http://dx.doi.org/10.1017/CBO9781139644105 - 2. Walls, D.F. and Milburn, G.J. (1994) Quantum Optics. Springer, Berlin Heidelberg.
http://dx.doi.org/10.1007/978-3-642-79504-6 - 3. Gardiner, C.W. and Zoller, P. (2004) Quantum Noise. Springer, Berlin Heidelberg.
http://www.amazon.com/Quantum-Noise-Non-Markovian-Applications-Synergetics/dp/3540223010 - 4. Moya-Cessa, H.M. and Soto-Eguibar, F. (2011) Introduction to Quantum Optics. Rinton Press, New Jersey.
http://www.rintonpress.com/books/0611.html - 5. Scully, M.O. and Zubairy, M.S. (1997) Quantum Optics. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511813993 - 6. Schleich, W. P. (2001) Quantum Optics in Phase Space. Wiley, Weinheim.
http://www.amazon.com/Quantum-Optics-Phase-Wolfgang-Schleich/dp/352729435X - 7. Kira, M. and Koch, S.W. (2011) Semiconductor Quantum Optics. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139016926 - 8. Agrawal, G.P. and Mehta, C.L. (1974) Dynamics of Parametric Processes with a Trilinear Hamiltonian. Journal of Physics A: Mathematical and General, 7, 607.
http://dx.doi.org/10.1088/0305-4470/7/5/011 - 9. Tucker, J. and Walls, D.F. (1969) Quantum Theory of Parametric Frequency Conversion. Annals of Physics, 52, 1-15.
http://dx.doi.org/10.1016/0003-4916(69)90318-2 - 10. Tang, C.L. (1969) Spontaneous Emission in the Frequency Up-Conversion Process in Nonlinear Optics. Physical Review, 182, 367.
http://dx.doi.org/10.1103/PhysRev.182.367 - 11. Tucker, J. and Walls, D.F. (1969) Quantum Theory of the Traveling-Wave Frequency Converter. Physical Review, 178, 2036.
http://dx.doi.org/10.1103/PhysRev.178.2036 - 12. Walls, D.F. and Barakat, R. (1970) Quantum-Mechanical Amplification and Frequency Conversion with a Trilinear Hamiltonian. Physical Review A, 1, 446.
http://dx.doi.org/10.1103/PhysRevA.1.446 - 13. Sebawe Abdalla, M. and Ahmed, M.M.A. (2012) Some Statistical Properties for a Spin-(1/2) Particle Coupled to Two Spirals. Optics Communications, 285, 3578-3586.
http://dx.doi.org/10.1016/j.optcom.2012.04.014 - 14. Eleuch, H. and Bennaceur, R. (2003) An Optical Soliton Pair among Absorbing Three-Level Atoms. Journal of Optics A: Pure and Applied Optics, 5, 528.
http://dx.doi.org/10.1088/1464-4258/5/5/315 - 15. Setea, E.A., Svidzinsky, A.A., Eleuch, H., Yang, Z., Nevels, R.D. and Scully, M.O. (2010) Correlated Spontaneous Emission on the Danube. Journal of Modern Optics, 57, 1311-1330.
http://dx.doi.org/10.1080/09500341003605445 - 16. Abdel-Aty, M. (2002) Influence of Second-Order Correction to Rayleigh Scattering on Pancharatnam Phase in a Three-Level Atom. Modern Physics Letters B, 16, 319.
http://dx.doi.org/10.1142/S0217984902003816 - 17. Abdel-Aty, M., Abdel-Khalek, S. and Obada, A.-S.F. (2000) Pancharatnam Phase of Two-Mode Optical Fields with Kerr Nonlinearity. Optical Review, 7, 499-504.
http://dx.doi.org/10.1007/s10043-000-0499-6 - 18. Bhandari, R. and Samuel, J. (1988) Observation of Topological Phase by Use of a Laser Interferometer. Physical Review Letters, 60, 1211.
http://dx.doi.org/10.1103/PhysRevLett.60.1211 - 19. Wagh, A.G. and Rakhecha, V.C. (1995) On Measuring the Pancharatnam Phase. I. Interferometry. Physics Letters A, 197, 107-111.
http://dx.doi.org/10.1016/0375-9601(94)00914-B - 20. Wagh, A.G. and Rakhecha, V.C. (1995) On Measuring the Pancharatnam Phase. II. SU(2) Polarimetry. Physics Letters A, 197, 112-115.
- 21. Zhao, Y.-G. and Li, B.-Z. (1997) Quantum Phases of Pancharatnam Type for a General Spin in a Time-Dependent Magnetic Field. Chinese Physics Letters, 14, 801.
http://dx.doi.org/10.1088/0256-307X/14/11/001 - 22. Lawande, Q.V., Lawande, S.V. and Joshi, A. (1999) Pancharatnam Phase for a System of a Two-Level Atom Interacting with a Quantized Field in a Cavity. Physics Letters A, 251, 164-168.
http://dx.doi.org/10.1016/S0375-9601(98)00882-2 - 23. Simon, B. (1983) Holonomy, the Quantum Adiabatic theoreM and Berry’s Phase. Physical Review Letters, 51, 2167.
http://dx.doi.org/10.1103/PhysRevLett.51.2167 - 24. Facchi, P., Mariano, A. and Pascazio, S. (1999) Wigner Function and Coherence Properties of Cold and Thermal Neutrons. Acta Physica Slovaca, 49, 677-682.
- 25. Jones, J.A., Vedral, V., Ekert, A. and Castagnoli, G. (2000) Geometric Quantum Computation Using Nuclear Magnetic Resonance. Nature, 403, 869-871.
http://dx.doi.org/10.1038/35002528 - 26. Pancharatnam (1956) Generalized Theory of Interference and Its Applications. S.Proc. Ind. Acad. Sci, 44, 247.
- 27. Francisco De Zela, F. (2012) The Pancharatnam-Berry Phase: Theoretical and Experimental Aspects. In: Pahlavani, M.R., Ed., Theoretical Concepts of Quantum Mechanics, Intech, 289.
http://dx.doi.org/10.5772/34882 - 28. Abdel-Khalek, S., El-Saman, Y.S. and Abdel-Aty, M. (2010) Geometric Phase of a Moving Three-Level Atom. Optics Communications, 283, 1826-1831.
http://dx.doi.org/10.1016/j.optcom.2009.12.065 - 29. van Dijk, T., Schouten, H.F., Ubachs, W. and Visser, T.D. (2010) The Pancharatnam-Berry Phase for Non-Cyclic Polarization Changes. Optics Express, 18, 10796-10804.
http://dx.doi.org/10.1364/OE.18.010796 - 30. Bhandari, R. (1989) Berry’s Phase and the Pancharatnam Angle-Some Recent Observations. Bulletin of the Calcutta Mathematical Society, 81, 496.
- 31. Hariharan, P. and Roy, M. (1992) A Geometric-Phase Interferometer. Journal of Modern Optics, 39, 1811-1815.
http://dx.doi.org/10.1080/09500349214551881 - 32. Masashi, B. (1993) Decomposition Formulas for Su(1, 1) and Su(2) Lie Algebras and Their Applications in Quantum Optics. Journal of the Optical Society of America B, 10, 1347-1359.
http://dx.doi.org/10.1364/JOSAB.10.001347 - 33. Sebawe Abdalla, M., Ahmed, M.M.A., Khalil, E.M. and Obada A.-S.F. (2014) Dynamics of an Adiabatically Effective Two-Level Atom Interacting with a Star-Like System. Progress of Theoretical and Experimental Physics, 2014, 073A02.
http://dx.doi.org/10.1093/ptep/ptu091











