Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:43826,7 pages DOI:10.4236/jqis.2014.41006
Approximate Quantum State Sharings via Pair of Private Quantum Channels
Dong Pyo Chi1, Kabgyun Jeong2
1Department of Mathematical Sciences, Seoul National University, Seoul, Korea
2School of Computational Sciences, Korea Institute for Advanced Study, Seoul, Korea
Email: kgjeong6@kias.re.kr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 January 2014; revised 22 February 2014; accepted 12 March 2014
ABSTRACT
We investigate a quantum communication protocol, of so-called approximate quantum state sharing (AQSS), that protocol is basically based on pair of private quantum channels. In this paper, we prove that the scheme is secure against any external and internal attacks of wiretapping in principle. Although the protocol leaks small amount of information corresponding to a security parameter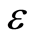 , the scheme still preserves its information-theoretic security.
, the scheme still preserves its information-theoretic security.
Keywords:Quantum State Sharing; (Approximate) Private Quantum Channel; Trace Norm

1. Introduction
Quantum physics promises perfect and well-defined randomness, in this way, most of all quantum information-theoretic primitives try to offer an unconditional security given by the quantum randomness. For examples, quantum key distribution protocols such as BB84 [1] and B92 [2] highly depend on prerequisite random measurements, assigning randomness, for some quantum states.
Instead of such random measurements on quantum states, we can consider a direct randomizing technique for quantum encodings through a quantum channel. (Mathematically quantum channel is a completely positive and trance-preserving map.) These randomizing procedures can be efficiently accomplished by exploiting the notion of private quantum channel (PQC) or quantum one-time pad [3] . In the paper, we are interesting to special scheme of an approximate version of encryption/decryption, although it is not perfect but we can make use of the protocol to attempt to reduce some quantum operation resources. We also call the map to randomizing quantum states as random unitary channel (RUC) in the sense of quantum channel. In the future, we will use the meaning of private quantum channel as equivalent as random unitary channel. There are several methods for approximate randomizing quantum states, for examples, [4] -[6] . We here adapt the encoding/decoding logic of the work of Hayden et al. [4] , and use the proof of Dickinson and Nayak’s trace norm method [6] . There are many applications of the private quantum channel in quantum information science [4] [7] [8] and it is mostly originated from the approximate version of PQC.
In this paper, we propose an approximate quantum state sharing (AQSS) scheme in which participants use two parallel approximate private quantum channels (APQC). The scheme reduces a secret and random string (classical pre-shared key) of about one-half as compare to the complete PQC protocol. Actually our protocol naturally includes the famous quantum secret sharing protocols [9] [10] in broad sense. Furthermore, quantum states in itself are able to operate some quantum tasks, though those are not possible in classical regime. Assume that if there is a quantum computer only activated by a bipartite quantum state (or bipartite quantum key), then our protocol AQSS may achieve the goal efficiently, and also offers new opportunities for quantum information processing.
We briefly review the key-sharing efficiency of AQSS for using pair of random unitary channels. Assume that (a sender) Charlie prepares a pure quantum state 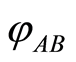 (two-qudit) and transmits the state to another distant receivers Alice and Bob through two independent RUCs. The transmitted state is generally maximally-mixed state. Then, for the state
(two-qudit) and transmits the state to another distant receivers Alice and Bob through two independent RUCs. The transmitted state is generally maximally-mixed state. Then, for the state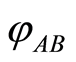 , perfect randomization protocol requires exactly the amount of
, perfect randomization protocol requires exactly the amount of 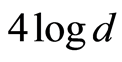 -bits of unitary operations (
-bits of unitary operations (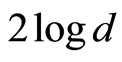 -bits for Alice and Bob, respectively), where
-bits for Alice and Bob, respectively), where  is the dimension of the input quantum state
is the dimension of the input quantum state 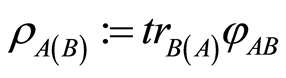 through each random unitary channels. On the other hand, the construction of Hayden et al.’ method [4] for a pair of random unitary channels implies that only
through each random unitary channels. On the other hand, the construction of Hayden et al.’ method [4] for a pair of random unitary channels implies that only 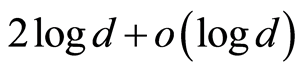 -bits of unitaries are sufficient. In other words, perfect quantum state sharing (QSS) protocol by using bilateral PQCs needs to
-bits of unitaries are sufficient. In other words, perfect quantum state sharing (QSS) protocol by using bilateral PQCs needs to 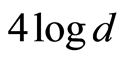 - bits of shared secret information, while the approximate QSS protocol (by using bilateral PQCs) demands about only
- bits of shared secret information, while the approximate QSS protocol (by using bilateral PQCs) demands about only 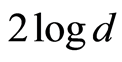 bits of classical information. Note that the works in [5] [6] give a similar result, but the lower bound for the key-information is little bit improved.
bits of classical information. Note that the works in [5] [6] give a similar result, but the lower bound for the key-information is little bit improved.
After an introduction to the definition of random unitary channel, we shortly mention about special properties of a destruction of quantum states in Section 2. Main part follows in Section 3. In Section 3, we present our AQSS protocol based on two approximate PQCs, and investigate the information-theoretic security of AQSS under considering two attacks such as exterior and interior strategies, respectively. We finally conclude our results in Section 4.
2. Random Unitary Channel and Its Properties
Now we define random unitary channel (or private quantum channel), and then explicitly construct the approximate version of private quantum channel. For any density matrices 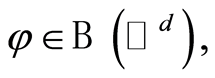 a completely positive and trace-preserving map
a completely positive and trace-preserving map 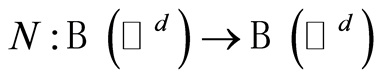 is said to be
is said to be  -randomizing, if
-randomizing, if
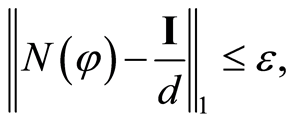 (1)
(1)
where the trace norm is defined by , and
, and 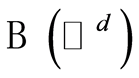 denotes the bounded linear operator on
denotes the bounded linear operator on 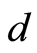 - dimensional (complex) Hilbert space
- dimensional (complex) Hilbert space 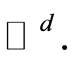 The character
The character 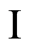 represents the
represents the 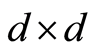 identity matrix on the space. This definition directly induces the notion of the RUC or PQC. That is, for every
identity matrix on the space. This definition directly induces the notion of the RUC or PQC. That is, for every 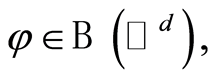 a quantum channel
a quantum channel 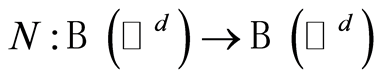 is called to private quantum channel, if the following construction
is called to private quantum channel, if the following construction
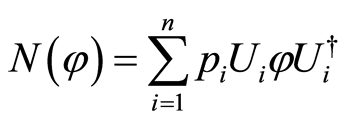 (2)
(2)
is  -randomizing, where the unitary operator
-randomizing, where the unitary operator  live in a unitary group
live in a unitary group , and the probability
, and the probability ’s are all positive and
’s are all positive and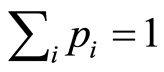 . Notice that the parameter
. Notice that the parameter 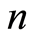 is closely related to the number of Kraus (operation) elements for establishing the private quantum channel. The perfect PQC demands on exactly
is closely related to the number of Kraus (operation) elements for establishing the private quantum channel. The perfect PQC demands on exactly  and this optimality condition is proved by several groups [11] [12] .
and this optimality condition is proved by several groups [11] [12] .
For the approximate constructions of PQC, it was known that for all 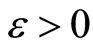 there exist a private quantum channel, in sufficiently larger dimension
there exist a private quantum channel, in sufficiently larger dimension 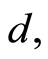 such that
such that 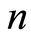 can be taken to be
can be taken to be 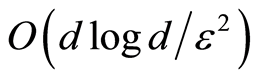 in [4] and
in [4] and 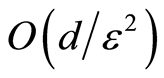 in [13] where
in [13] where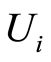 ’s are chosen randomly according to the unitarily invariant measure (or Haar measure). We here fix the number
’s are chosen randomly according to the unitarily invariant measure (or Haar measure). We here fix the number 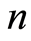 of having exactly
of having exactly 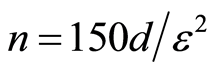 from the Theorem 1 in [13] . As mentioned in Introduction, most applications of private quantum channel are closely connected to the approximate version of the private quantum channel [4] . That is, approximate PQC is the main tool for constructing following AQSS protocol.
from the Theorem 1 in [13] . As mentioned in Introduction, most applications of private quantum channel are closely connected to the approximate version of the private quantum channel [4] . That is, approximate PQC is the main tool for constructing following AQSS protocol.
The security of PQC is conserved by the argument of the accessible information in which leakage information is less than sufficiently small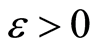 . Although small leakage-information can be attacked to an eavesdropper (Eve), the Bob’s decoding state is almost equal to the Alice’s original state
. Although small leakage-information can be attacked to an eavesdropper (Eve), the Bob’s decoding state is almost equal to the Alice’s original state . Figure 1 describes the total procedure of PQC. (The double line describes a classical channel for secret bits between Alice and Bob.)
. Figure 1 describes the total procedure of PQC. (The double line describes a classical channel for secret bits between Alice and Bob.)
2.1. Bilateral Private Quantum Channel
In this subsection we introduce a bilateral form of private quantum channels. These channels will be used to create following (approximate) QSS scheme in Section 3. First of all, we consider that two one-way independent PQCs are constituted between a sender Charlie and a receiver Alice, and Charlie and another receiver Bob, simultaneously. Then, let us define two PQCs, following the definition of Equation (2), such that
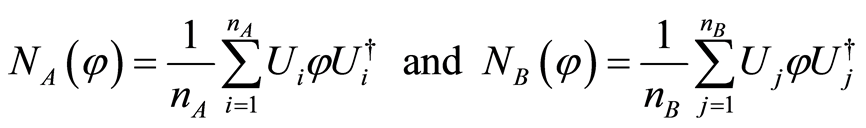 (3)
(3)
are 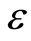 -randomizing maps, where we fix a probability as equally weighted probabilities
-randomizing maps, where we fix a probability as equally weighted probabilities  and
and
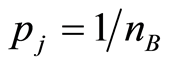 for all
for all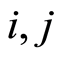 . For convenience, the number of
. For convenience, the number of 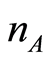 is fixed exactly equal to
is fixed exactly equal to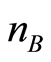 , i.e.,
, i.e.,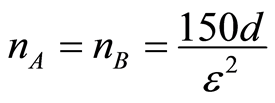 .
.
As mentioned above, for an approximate, but secure, state sharing of any bipartite quantum states (either separable or entangled), those two channels play an important role to making approximate quantum state sharing scheme later.
For given 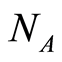 and
and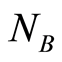 , and for all input
, and for all input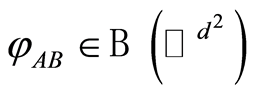 , we can bound the trace norm for the difference between a channel-output state of product channel
, we can bound the trace norm for the difference between a channel-output state of product channel 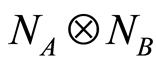 and the maximally mixed state
and the maximally mixed state 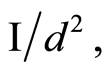 such that
such that
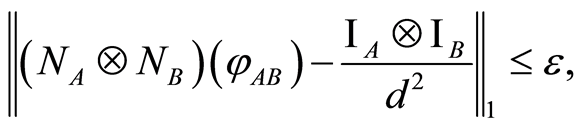 (4)
(4)
where a security parameter 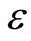 is small and positive, but less than 1. The inequality above asserts that all encoding states are information-theoretically secure. Unfortunately, for any entangled state
is small and positive, but less than 1. The inequality above asserts that all encoding states are information-theoretically secure. Unfortunately, for any entangled state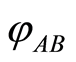 , calculation of the bound is not a trivial task.
, calculation of the bound is not a trivial task.
Here we notice that the efficiency argument for the randomizing procedure is intimately related to the destruction of correlations in the quantum states [4] [14] . Another words, if we desire to completely destroy the total correlation in the channel-output states, then we are needed to unitary operations of the amount of corresponding to the quantum mutual information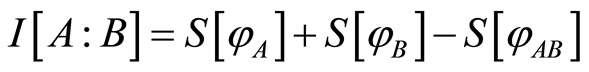 , where
, where  the von Neumann entropy for given quantum state
the von Neumann entropy for given quantum state 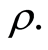 For example, a maximally entangled state
For example, a maximally entangled state  has precisely
has precisely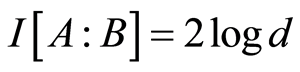 , so we guess the asymptotic amount of quantum operations needed. Formally speaking, the Equation (4), can be inferred from triangle inequality with respect to the
, so we guess the asymptotic amount of quantum operations needed. Formally speaking, the Equation (4), can be inferred from triangle inequality with respect to the
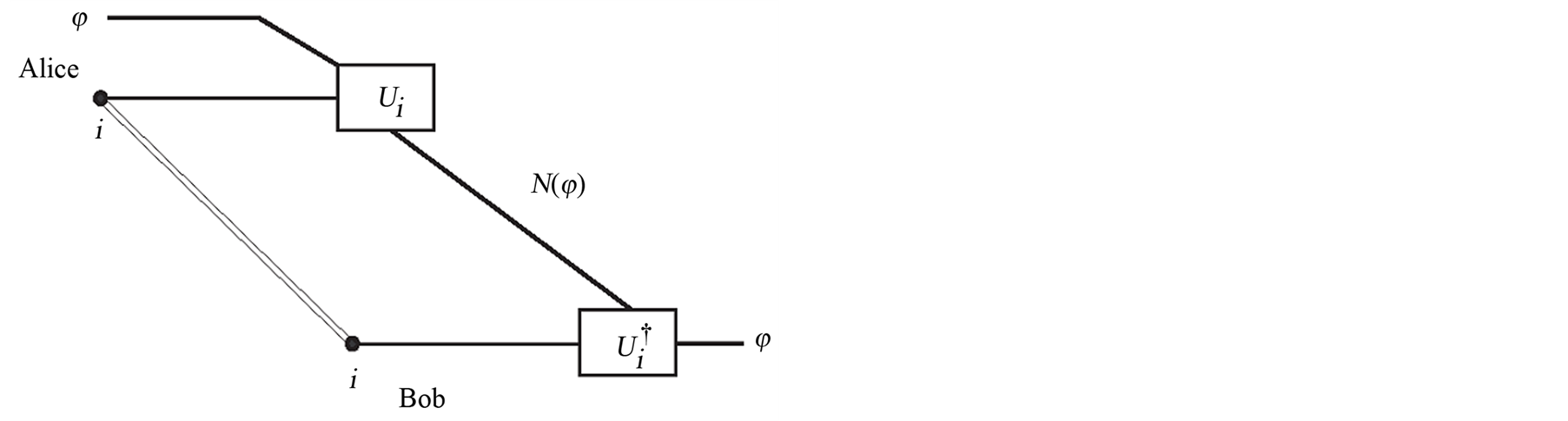
Figure 1. Private quantum channel: Alice applies Ui’s for encoding of φ and Bob decodes N(φ) with a secret key i which is pre-shared log n-bits of classical information.
trace norm on two PQCs, i.e., suppose that 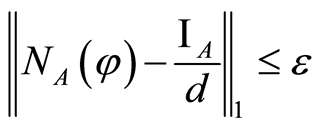 and
and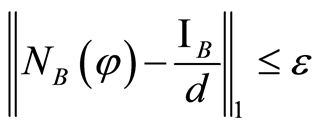 , then we have
, then we have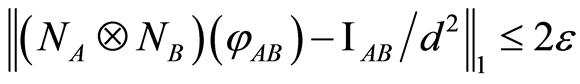 . (See the proof of the Proposition 1 in [14] .) In Appendix of this paper, we examine the inequality precisely by exploiting the relation between the trace and Hilbert-Schmidt norms.
. (See the proof of the Proposition 1 in [14] .) In Appendix of this paper, we examine the inequality precisely by exploiting the relation between the trace and Hilbert-Schmidt norms.
3. Approximate Quantum State Sharing Protocol
In this section we construct a scheme of so-called approximate quantum state sharing. Suppose that Charlie-Alice and Charlie-Bob are linked by independent two quantum communication channels of such approximate private quantum channels, which endow the outputs of  -dimensional maximally mixed states, respectively. First of all, Charlie prepares (arbitrary) bipartite quantum state
-dimensional maximally mixed states, respectively. First of all, Charlie prepares (arbitrary) bipartite quantum state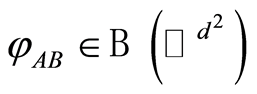 , it does not matter the state of pure or mixed. He wants to securely transmit
, it does not matter the state of pure or mixed. He wants to securely transmit 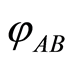 to Alice and Bob together, and then to reconstruct the cleft state to original one on Alice and Bob’s site via mutual cooperation. The total procedure of transmitting-reconstructing scheme, for a bipartite quantum state sharing, is quite simple, more specifically the scheme has only three steps:
to Alice and Bob together, and then to reconstruct the cleft state to original one on Alice and Bob’s site via mutual cooperation. The total procedure of transmitting-reconstructing scheme, for a bipartite quantum state sharing, is quite simple, more specifically the scheme has only three steps:
• Sender Charlie prepares two-qudit , and transmit the state through the channel
, and transmit the state through the channel 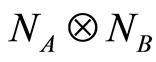 to two receivers Alice and Bob.
to two receivers Alice and Bob.
• Distant two parties Alice and Bob just hold the state they received, until they need the information of the quantum state.
• When Alice and Bob want to reveal the original state , they must clearly cooperate in a single location. They perform inverse unitary operations based on the locally shared classical secret-key information.
, they must clearly cooperate in a single location. They perform inverse unitary operations based on the locally shared classical secret-key information.
The security check of the AQSS protocol is divided by two cases of exterior and interior attacks. Actually the security is based on information-theoretic assumption, which means that the intercepted states by Eve have sufficiently higher von Neumann entropy. Thus any attacks on the channel are impossible to be obtained any information to revealing the original quantum information.
First, let us take account of an attack accomplished by an external Eve. Suppose that if Eve intercepts the state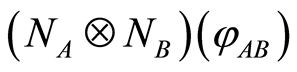 , we hope that the state has higher entropic condition. In this reason, we propose that the entropy of the channel-output state to be following
, we hope that the state has higher entropic condition. In this reason, we propose that the entropy of the channel-output state to be following
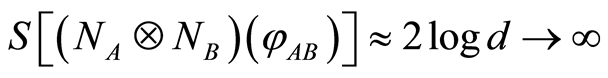 (5)
(5)
as 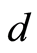 goes to infinity. (The notation “
goes to infinity. (The notation “ ” denotes that left side is “approximately equal to” right side.) We do not know the accurate description for the state
” denotes that left side is “approximately equal to” right side.) We do not know the accurate description for the state 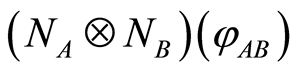 right now, so we divide the input state
right now, so we divide the input state 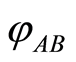 into cases of separable and entangled, and prove its entropic condition. If product state is given, then it is possible to prove the inequality Equation (4) easily. Since, by using the triangle inequality once again with respect to the trace norm, the following inequality
into cases of separable and entangled, and prove its entropic condition. If product state is given, then it is possible to prove the inequality Equation (4) easily. Since, by using the triangle inequality once again with respect to the trace norm, the following inequality  holds for any
holds for any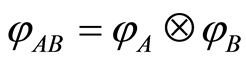 . If we generally assume that
. If we generally assume that 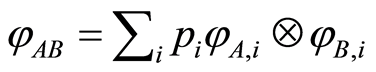 a separable state, then we have
a separable state, then we have
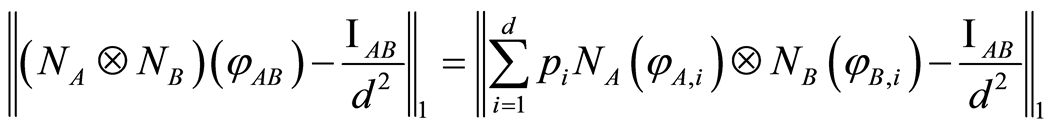
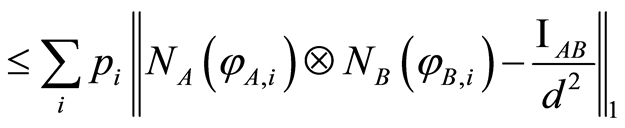 (6)
(6)
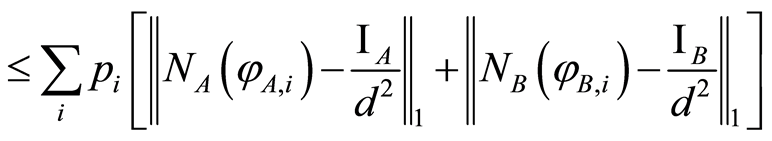 (7)
(7)

where the inequalities Equations (6) and (7) are derived from the norm convexity and triangle inequality, respectively. Thus any separable inputs for the product channel are very close to the maximally mixed state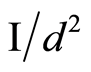 . This implies that
. This implies that 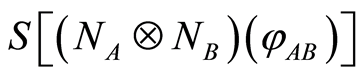 is equal to
is equal to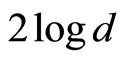 .
.
For the separable input cases, there is another proof that depends on the dimension parameter 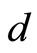 and
and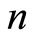 : We can prove that the expectation value for the difference between the output of the quantum channel and the maximally mixed state (with respect to the trace norm) is bounded by a small quantity (dimension related)
: We can prove that the expectation value for the difference between the output of the quantum channel and the maximally mixed state (with respect to the trace norm) is bounded by a small quantity (dimension related)
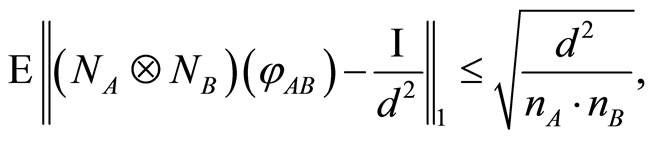 (8)
(8)
where 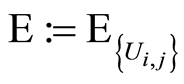 denotes the total expectation of
denotes the total expectation of 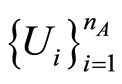 and
and 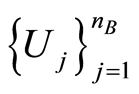 for the independent PQCs
for the independent PQCs 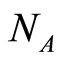 and
and , respectively. The Appendix in this paper shows that the inequality Equation (8) can be derived precisely by exploiting the relation between the trace norm and Hilbert-Schmidt norm. As mentioned above, when one takes
, respectively. The Appendix in this paper shows that the inequality Equation (8) can be derived precisely by exploiting the relation between the trace norm and Hilbert-Schmidt norm. As mentioned above, when one takes 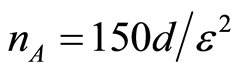 and
and 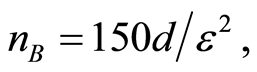 then we have
then we have
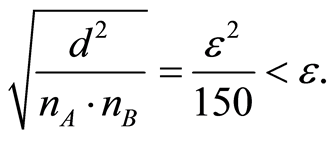 (9)
(9)
This implies that Eve’s attack is impossible in principle. Then how can we treat of entangled input states? Although direct proof is impossible, there is an evidence for the statement on Equation (5). The Theorem III.3 in [4] states that, for a positive operator-valued measure (POVM)  which is implemented by using local operation and classical communication (LOCC),
which is implemented by using local operation and classical communication (LOCC),
 is true, where
is true, where 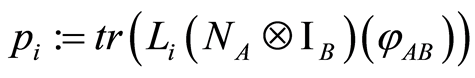 and
and 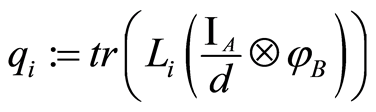 with a maximally entangled state such that
with a maximally entangled state such that  and
and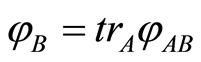 . Natural extension to channel
. Natural extension to channel  is possible via adding the channel
is possible via adding the channel : Define
: Define 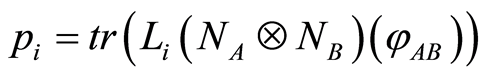 and
and 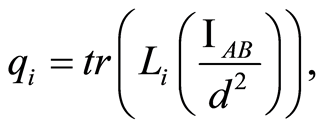 then also we have
then also we have 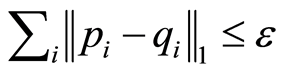 Therefore, we can conclude that an output state of the product channel,
Therefore, we can conclude that an output state of the product channel, 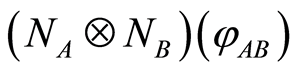 , is close to
, is close to 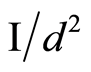 under the LOCC-implemented POVM. In this reason, any input entangled states
under the LOCC-implemented POVM. In this reason, any input entangled states  through the product channel
through the product channel 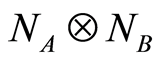 has always high entropy condition for
has always high entropy condition for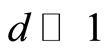 .
.
Second, we take care of a situation when Alice or Bob is malicious. Assume that Bob intercepts the Alice’s state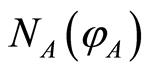 , but Bob’s state decoded will be
, but Bob’s state decoded will be
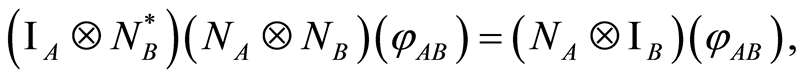 (10)
(10)
where * denotes the inverse (unitary) operation for Bob’s PQC , so
, so 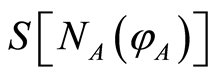 for the resulting state has still higher entropy such as
for the resulting state has still higher entropy such as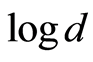 . Because the intercepted state
. Because the intercepted state 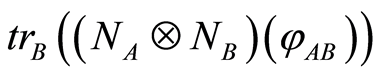 is almost maximally mixed state by the definition of PQC
is almost maximally mixed state by the definition of PQC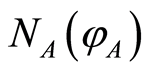 . Thus, Bob cannot obtain any information for
. Thus, Bob cannot obtain any information for 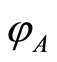 without Alice's secret key information. Symmetrically, Alice’s attack is also useless. In other words, Charlie’s aim of sharing a quantum state
without Alice's secret key information. Symmetrically, Alice’s attack is also useless. In other words, Charlie’s aim of sharing a quantum state 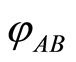 between Alice and Bob can be securely accomplished. At least two attacks of external and internal eavesdroppings cannot break the security condition of our AQSS protocol. Furthermore, only cooperation between Alice and Bob always gives birth to the original state.
between Alice and Bob can be securely accomplished. At least two attacks of external and internal eavesdroppings cannot break the security condition of our AQSS protocol. Furthermore, only cooperation between Alice and Bob always gives birth to the original state.
We notice that perfect protocol for QSS requires exactly  unitary operators as mentioned above, while our protocol is only needed to total
unitary operators as mentioned above, while our protocol is only needed to total 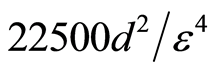 unitaries. This fact directly implies that some shared key bits can be reduced about
unitaries. This fact directly implies that some shared key bits can be reduced about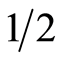 . Because our AQSS is just needed
. Because our AQSS is just needed 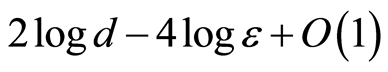 secret bits, but perfect QSS is required
secret bits, but perfect QSS is required 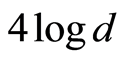 bits. In summary of this section, for any state
bits. In summary of this section, for any state  and a quantum channel
and a quantum channel 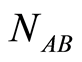 (for an
(for an 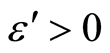 is arbitrary), assume that following inequality
is arbitrary), assume that following inequality
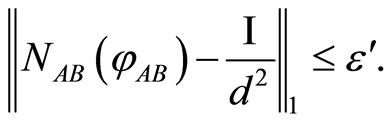 (11)
(11)
Then, it is sufficient to create a perfect QSS 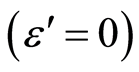 with
with 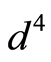 unitary operations [4] [6] . In the case, our approximate QSS via pair of two PQCs,
unitary operations [4] [6] . In the case, our approximate QSS via pair of two PQCs, 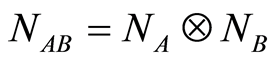 , just consume of one-half secret classical bits. Thus we can say that it is efficient.
, just consume of one-half secret classical bits. Thus we can say that it is efficient.
Finally we remark that a direct generalization is possible for the bipartite quantum state sharing (Equation (8)) scheme to a multiparty approximate quantum state sharing (MAQSS), and the secrecy is also preserved. Suppose that a situation of Charlie  prepares an
prepares an 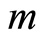 -qudit quantum state
-qudit quantum state 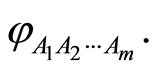 If they had secret bitstrings for PQCs between
If they had secret bitstrings for PQCs between 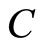 -
-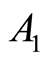 ,
, 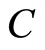 -
- and so on, then we have
and so on, then we have
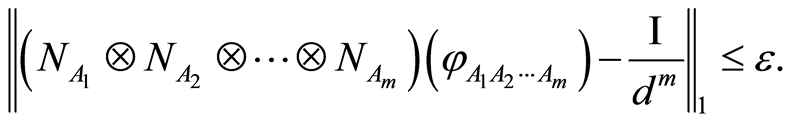 (12)
(12)
Equation (12) implies that any exterior attacks are failed, as well as all interior attacks (including group conspiracy) are also to be frustrated, since, without secret-bits of another participants, it is similar to the two receiver cases. We briefly mention about the cost of secret classical information on MAQSS scheme. Roughly speaking, the perfect scheme requires 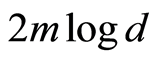 classical bits, but the MAQSS only
classical bits, but the MAQSS only 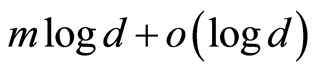 -bits are sufficient. As an alternative of the study on multiparty AQSS protocol, in the near future we will analyze that a generalized security proof of AQSS with respect to the Shatten
-bits are sufficient. As an alternative of the study on multiparty AQSS protocol, in the near future we will analyze that a generalized security proof of AQSS with respect to the Shatten 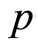 -norms beyond the trace case.
-norms beyond the trace case.
4. Conclusion
We studied that an approximate quantum state sharing scheme is efficient from the classical information cost of view and the protocol is robust to the two kinds (internal and external) of wiretappings from the construction via bilateral private quantum channel. Especially, we analyzed that given protocol is strong under the channel-inputs of all separable and entangled quantum states. The proposed AQSS protocol basically depends on approximate private quantum channels, which are essentially equivalent to pair of independent random unitary channels. Although the protocol leaks small information corresponding to a security parameter , we can conclude that the scheme preserves its information-theoretic security for any bipartite quantum states.
, we can conclude that the scheme preserves its information-theoretic security for any bipartite quantum states.
Acknowledgements
This work was partly supported by the IT R\&D program of MOTIE/KEIT [10043464 (2013)].
References
- Bennett, C.H. and Brassard, G. (1984) Quantum Cryptography: Public Key Distribution and Coin Tossing. Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, Bangalore, 175-179.
- Bennett, C.H. (1992) Quantum Cryptography Using Any Two Nonorthogonal States. Physical Review Letters, 68, 3121. http://dx.doi.org/10.1103/PhysRevLett.68.3121
- Ambainis, A., Mosca, M., Tapp, A. and de Wolf, R. (2000) Private Quantum Channels. IEEE Symposium on Foundations of Computer Sciences (FOCS), 547-553.
- Hayden, P., Leung, D., Shor, P.W. and Winter, A. (2004) Randomizing Quantum States: Constructions and Applications. Communication in Mathematical Physics, 250, 371-391. http://dx.doi.org/10.1007%2Fs00220-004-1087-6
- Ambainis, A. and Smith, A. (2004) Small Pseudo-Random Families of Matrices: Derandomizing Approximate Quantum Encryption. Proceedings of RANDOM, LNCS 3122, Springer, Berlin-Heidelberg-New York.
- Dickinson, P.A. and Nayak, A. (2006) Approximate Randomization of Quantum States With Fewer Bits of Key. AIP Conference Proceedings, 864, 18. http://dx.doi.org/10.1063/1.2400876
- Harrow, A., Hayden, P. and Leung, D. (2004) Superdense Coding of Quantum States. Physical Review Letters, 92, Article ID: 187901. http://dx.doi.org/10.1103/PhysRevLett.92.187901
- Bennett, C.H., Hayden, P., Leung, D., Shor, P.W. and Winter, A. (2006) Remote Preparation of Quantum States. IEEE Transactions on Information Theory, 51, 56-74. http://dx.doi.org/10.1109/TIT.2004.839476
- Hillery, M., Bužek, V. and Berthiaume, A. (1999) Quantum Secret Sharing. Physical Review A, 59, 1829. http://dx.doi.org/10.1103/PhysRevA.59.1829
- Karlsson, A., Koashi, M. and Imoto, N. (1999) Quantum Entanglement for Secret Sharing and Secret Splitting. Physical Review A, 59, 162. http://dx.doi.org/10.1103/PhysRevA.59.162
- Nagaj, D. and Kerenidis, I. (2006) On the Optimality of Quantum Encryption Schemes. Journal of Mathematical Physics, 47, Article ID: 092102. http://dx.doi.org/10.1063/1.2339014
- Bouda, J. and Ziman, M. (2007) Optimality of Private Quantum Channels. Journal of Physics A: Mathematical and Theoretical, 40, 5415. http://dx.doi.org/10.1088/1751-8113/40/20/011
- Aubrun, G. (2009) On Almost Randomizing Channels with a Short Kraus Decomposition. Communication in Mathematical Physics, 288, 1103-1116. http://dx.doi.org/10.1007/s00220-008-0695-y
- Groisman, B., Popescu, S. and Winter, A. (2005) Quantum, Classical, and Total Amount of Correlations in a Quantum state. Physical Review A, 72, Article ID: 032317. http://dx.doi.org/10.1103/PhysRevA.72.032317
Appendix
For given two random unitary channels 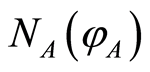 and
and 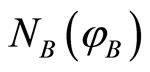 in Equation (3), and for all pure separable states
in Equation (3), and for all pure separable states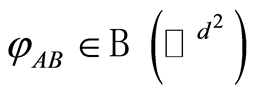 ,
,
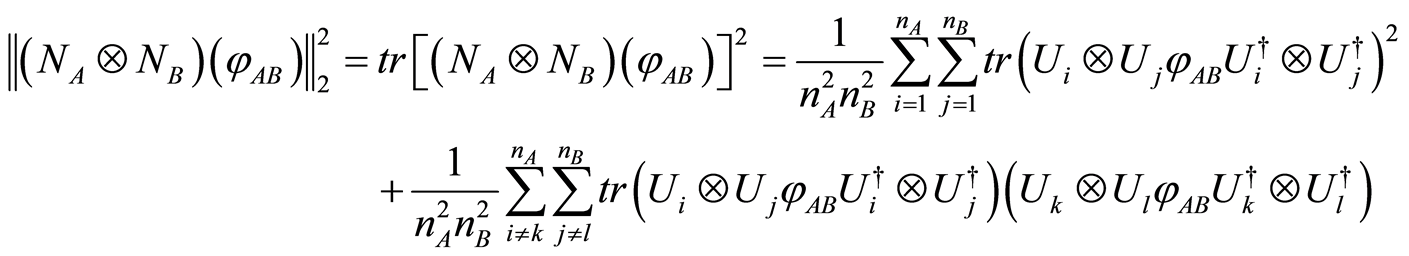 (13)
(13)
where 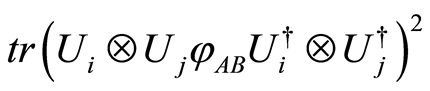 for any pure state
for any pure state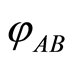 . (Note that this method is just an expansion of the statement, the chapter 3, in [8] .)
. (Note that this method is just an expansion of the statement, the chapter 3, in [8] .)
Recall that the unitary operators are chosen randomly according to the unitarily invariant (Haar) measure, and if we take the expectation over all random selection of unitaries, then
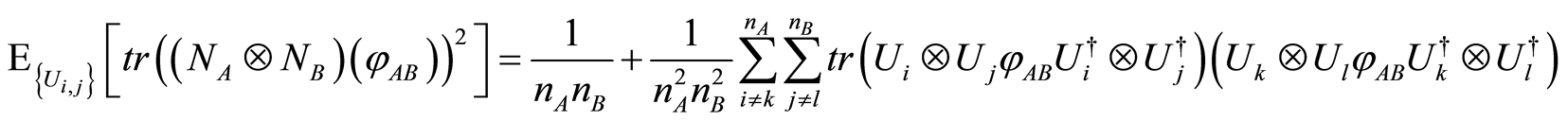
 (14)
(14)
 (15)
(15)
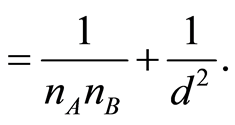 (16)
(16)
In Equation (14), we make use of the fact that the sets of unitary operators 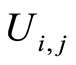 and
and 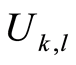 are chosen independently at random, and the Equation (15) is inherited from the definition of the Haar measure on the unitary group. (Notice that for any
are chosen independently at random, and the Equation (15) is inherited from the definition of the Haar measure on the unitary group. (Notice that for any 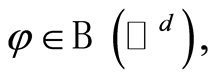 a Haar-distributed unitary set
a Haar-distributed unitary set 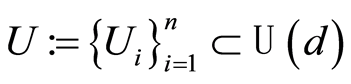 satisfies that
satisfies that
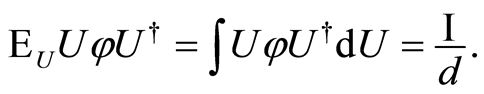 ) The Equation (15) exploits the separable condition for
) The Equation (15) exploits the separable condition for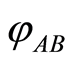 . Note that, for any rank
. Note that, for any rank  matrix
matrix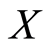 ,
,  , actually it is the very Cauchy-Schwartz inequality. For any rank
, actually it is the very Cauchy-Schwartz inequality. For any rank 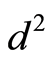 matrix
matrix , a generalization of the Corollary A.2 in [8] directly shows that
, a generalization of the Corollary A.2 in [8] directly shows that
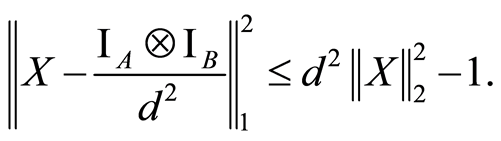 (17)
(17)
Then, from considering the random variable 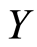 defined by
defined by  and by using Equation (16), we have
and by using Equation (16), we have
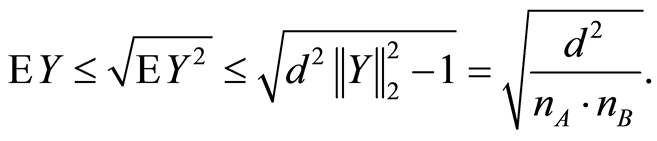 (18)
(18)

