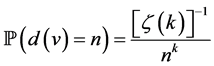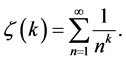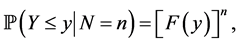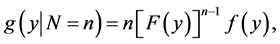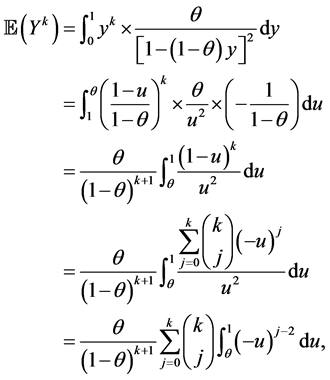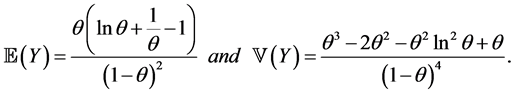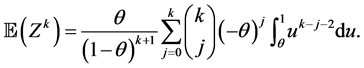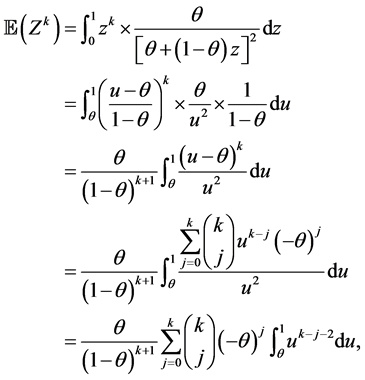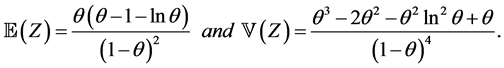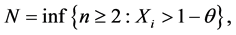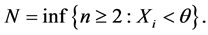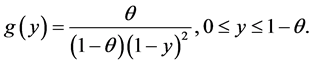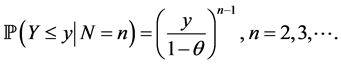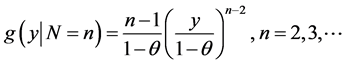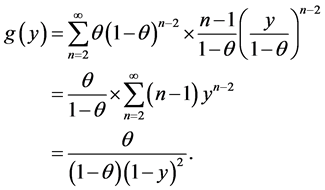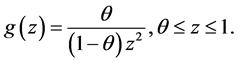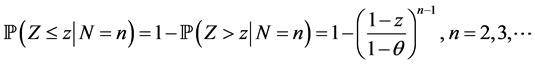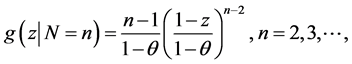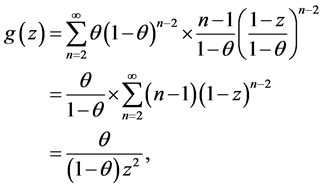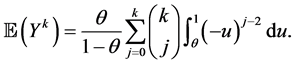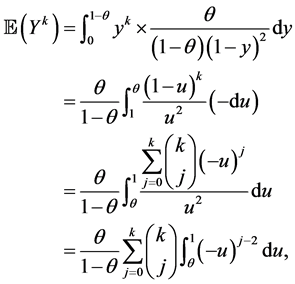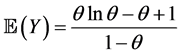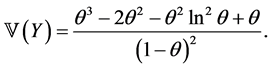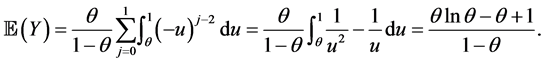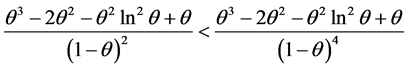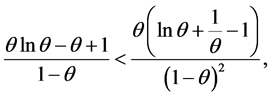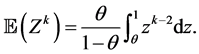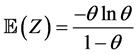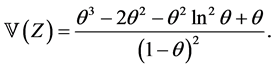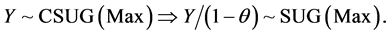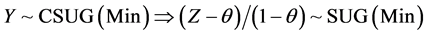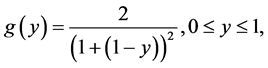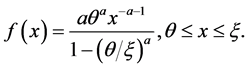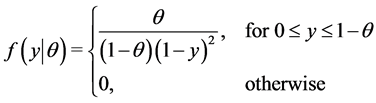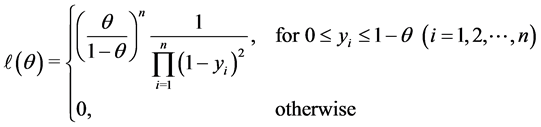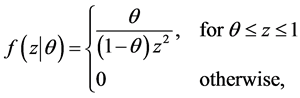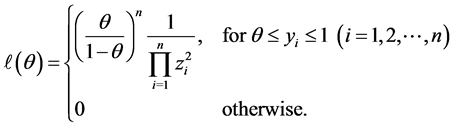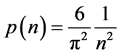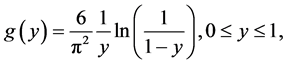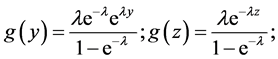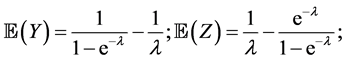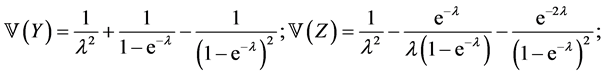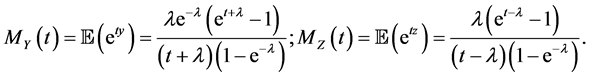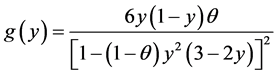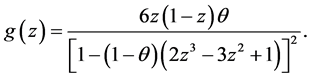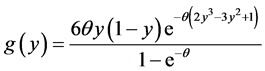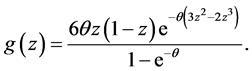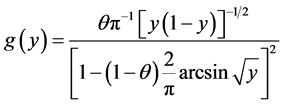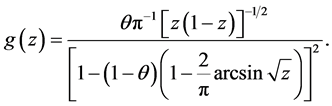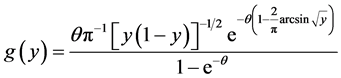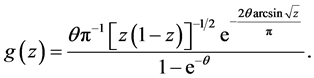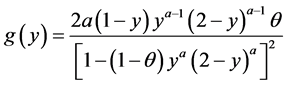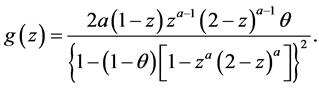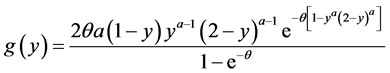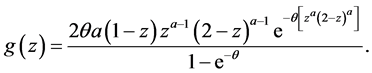Open Journal of Statistics
Vol.06 No.02(2016), Article ID:65869,12 pages
10.4236/ojs.2016.62023
Distribution of the Maximum and Minimum of a Random Number of Bounded Random Variables
Jie Hao1, Anant Godbole2
1Department of Statistics and Analytical Sciences, Kennesaw State University, Kennesaw, USA
2Department of Mathematics and Statistics, East Tennessee State University, Johnson City, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2016; accepted 23 April 2016; published 26 April 2016
ABSTRACT
We study a new family of random variables that each arise as the distribution of the maximum or minimum of a random number N of i.i.d. random variables X1, X2, ∙∙∙, XN, each distributed as a variable X with support on [0, 1]. The general scheme is first outlined, and several special cases are studied in detail. Wherever appropriate, we find estimates of the parameter θ in the one-parameter family in question.
Keywords:
Maximum and Minimum, Random Number of i.i.d. Variables, Statistical Inference

1. Introduction
Consider a sequence 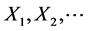 of i.i.d. random variables with support on
of i.i.d. random variables with support on 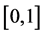 and having distribution function F. For any fixed n, the distributions of
and having distribution function F. For any fixed n, the distributions of
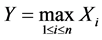
and
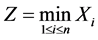
have been well studied; in fact it is shown in elementary texts that 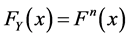 and
and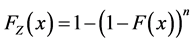 . But what if we have a situation where the number N of Xi’s is random, and we are instead considering the extrema
. But what if we have a situation where the number N of Xi’s is random, and we are instead considering the extrema
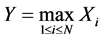 (1)
(1)
and
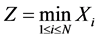 (2)
(2)
of a random number of i.i.d. random variables? Now the sum S of a random number of i.i.d. variables, defined as
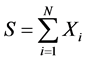
satisfies, according to Wald’s Lemma [1] , the equation
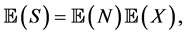
provided that N is independent of the sequence 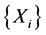 and assuming that the means of X and N exist.
and assuming that the means of X and N exist.
The purpose of this paper is to show that the distributions in (1) and (2) can be studied in many canonical cases, even if N and 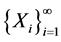 are correlated. The main deviation from the papers [2] [3] and [4] , where similar questions are studied, is that the variable X is concentrated on the interval
are correlated. The main deviation from the papers [2] [3] and [4] , where similar questions are studied, is that the variable X is concentrated on the interval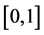 ―unlike the above references, where X has lifetime-like distributions on
―unlike the above references, where X has lifetime-like distributions on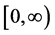 . Even then, we find that many new and interesting distributions arise, none of them to be found, e.g., in [5] or [6] via the “extreme values of a random number of i.i.d. variables” connection. See, however, Remarks 1 and 2 in Section 3. In another deviation from the theory of extremes of random sequences (see, e.g., [7] ), we find that the tail behavior of the extreme distributions is not relevant due to the fact that the distributions have compact support. We next cite three examples where our methods might be useful. First, we might be interested in the strongest earthquake in a given region in a given year. The number of earthquakes in a year, N, is usually modeled using a Poisson distribution, and, ignoring aftershocks and similarly correlated events, the intensities of the earthquakes can be considered to be i.i.d. random variables in
. Even then, we find that many new and interesting distributions arise, none of them to be found, e.g., in [5] or [6] via the “extreme values of a random number of i.i.d. variables” connection. See, however, Remarks 1 and 2 in Section 3. In another deviation from the theory of extremes of random sequences (see, e.g., [7] ), we find that the tail behavior of the extreme distributions is not relevant due to the fact that the distributions have compact support. We next cite three examples where our methods might be useful. First, we might be interested in the strongest earthquake in a given region in a given year. The number of earthquakes in a year, N, is usually modeled using a Poisson distribution, and, ignoring aftershocks and similarly correlated events, the intensities of the earthquakes can be considered to be i.i.d. random variables in 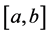 whose distribution can be modeled using, e.g., the data set maintained by Caltech at [8] . Second, many “small world” phenomena have recently been modeled by power law distributions, also sometimes termed discrete Pareto or Zipf distributions. See, for example, the body of work by Chung and her co-authors [9] [10] , and the references therein, where vertex degrees
whose distribution can be modeled using, e.g., the data set maintained by Caltech at [8] . Second, many “small world” phenomena have recently been modeled by power law distributions, also sometimes termed discrete Pareto or Zipf distributions. See, for example, the body of work by Chung and her co-authors [9] [10] , and the references therein, where vertex degrees 
for some constant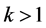
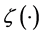
Thus if the vertices v in a large internet graph have some bounded i.i.d. property Xi, then the maximum and minimum values of Xi for the neighbors of a randomly chosen vertex can be modeled using the methods of this paper. Third, we note that N and the Xi may be correlated, as in the CSUG example (studied systematically in Section 3) where 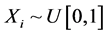
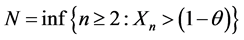
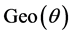
Here is our general set-up: Suppose 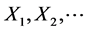
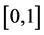
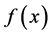
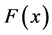
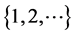
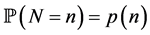
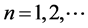
we see that
and consequently, the marginal p.d.f. of Y is
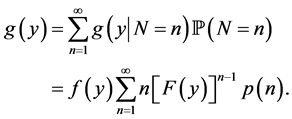
In a similar fashion, the p.d.f. of Z can be shown to be
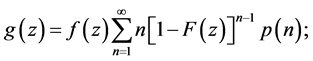
what is remarkable is that the sums in (3) and (4) will be shown to assume simple tractable forms in a variety of cases.
We want to point out that some of our distributions have been studied before but not using this motivation. For example, the Marshall-Olkin distributions [11] give a new method of adding a parameter to a distribution. Also, other distributions such as the beta and Kumaraswamy [12] distributions can be used to model continuous bounded data, but these do not apply to our set-up. See also Remark 2 in Section 3.
Our paper is organized as follows. Section 1 provided a summary and motivation for studying the distributions in the fashion we do. In Section 2, we study the case of 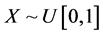
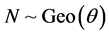
2. Standard Uniform Geometric (SUG) Model
Since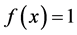
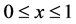
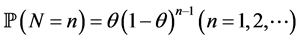
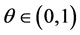
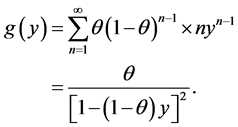
Similarly, (4) gives that
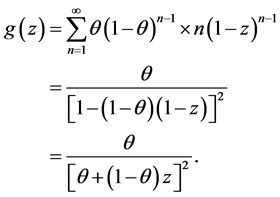
Proposition 2.1. If the random variable Y has the “SUG maximum distribution” (5) and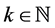
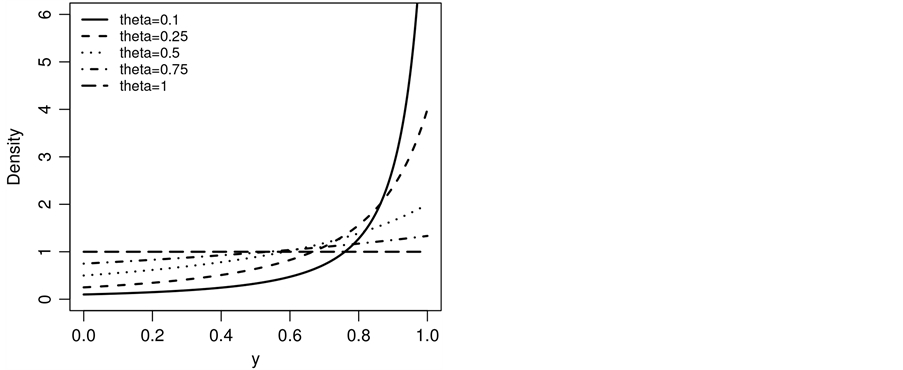
Figure 1. Plot of the SUG maximum density for some values of θ (see Equation (5)).
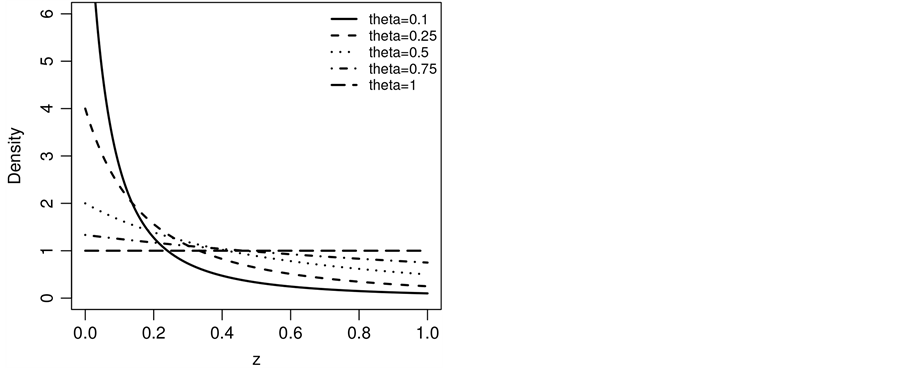
Figure 2. Plot of the SUG minimum density for some values of θ (see Equation (6)).
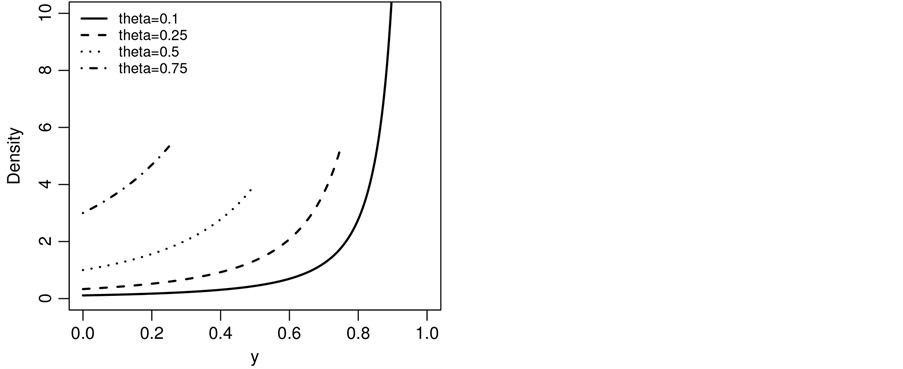
Figure 3. Plot of the CSUG maximum density for some values of θ.
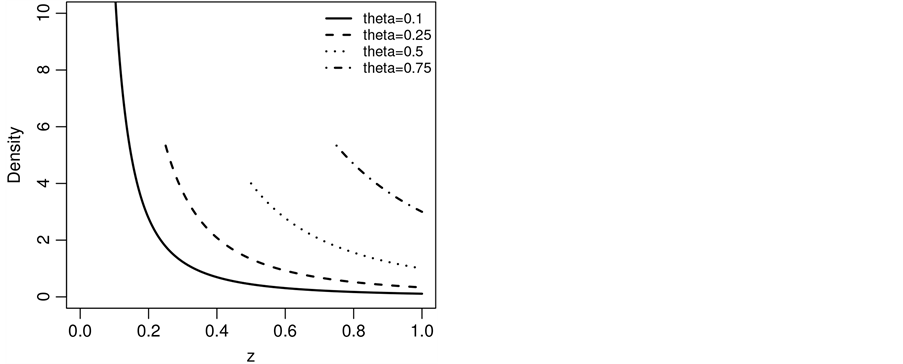
Figure 4. Plot of CSUG minimum density for some values of θ.
as claimed. □
Note. Even though we take the distributions to have support on
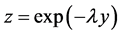
Proposition 2.2. The random variable Y has mean and variance given, respectively, by
Proof. Using Proposition 2.1, we can directly compute the mean and variance by setting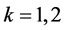
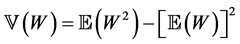
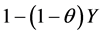
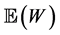
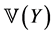
Proposition 2.3. If the random variable Z has the “SUG minimum distribution” and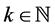
Proof.
as asserted. □
Proposition 2.4. The random variable Z has mean and variance given, respectively, by
Proof. Using Proposition 2.3, it is easily to compute the mean and variance by setting k = 1, k = 2. □
The m.g.f.’s of Y, Z are easy to calculate too. Notice that the logarithmic terms above arise due to the contributions of the j = 1 and 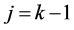
3. The Correlated Standard Uniform Geometric (CSUG) Model
The Correlated Standard Uniform Geometric (CSUG) model is related to the SUG model, as the name suggests, but X and N are correlated as indicated in Section 1. The CSUG problems arise in two cases. One case is that we conduct standard uniform trials until a variable Xi exceeds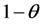
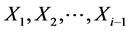
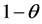
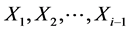
Specifically, let 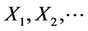
or
In either case N has probability mass function given by
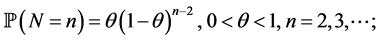
note that this is simply a geometric random variable conditional on the success having occurred at trial 2 or later. Clearly N is dependent on the X sequence.
Proposition 3.1. Under the CSUG model, the p.d.f. of Y, defined by (1), is given by
Proof. The conditional c.d.f. of Y given that 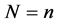
Taking the derivative, we see that the conditional density function is given by
Consequently, the p.d.f. of Y in the CSUG model is given by
This completes the proof. □
Proposition 3.2. The p.d.f. of Z under the CSUG model is given by
Proof. The conditional cumulative distribution function of Z given that 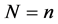
Thus, the conditional density function is given by
which yields the p.d.f. of Z under the CSUG model as
which finishes the proof. □
Proposition 3.3. If the random variable Y has the “CSUG maximum distribution” and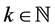
Proof.
as claimed. □
Proposition 3.4. The random variable Y has mean and variance given, respectively, by
and
Proof. Using Proposition 3.3, we can directly compute the mean and variance by setting k = 1, 2. For example with k = 1 we get
Notice that the variance of Y is smaller than that of Y under the SUG model, with an identical numerator term. Also, the expected value is smaller under the CSUG model than in the SUG case. This can be best seen by the inequalities
and
valid for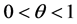
Proposition 3.5. If the random variable Z has the “CSUG Minimum distribution” and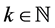
Proof. Routine, as before. □
Proposition 3.6. The random variable Z has mean and variance given, respectively, by
and
Proof. A special case of Proposition 3.3; note that as in the SUG model,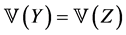
Remark 1. The four distributions of Y and Z under the SUG and the CSUG models can be shown to be affine transformations of the same distribution as seem by the following results (proofs omitted):
Proposition 3.7. Changing the variable Y of (5) as 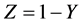
Proposition 3.8. Changing the variable Y of the CSUG model (in Proposition 3.1) as 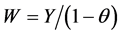
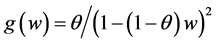
Proposition 3.9. Changing the variable Z of the CSUG model (in Proposition 3.2) as 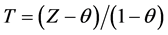
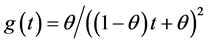
As a result of these affine transformations, the moment equations (Propositions from 2.1 to 2.4 and from 3.3 to 3.6) can be derived in an easier fashion, though these facts are easier to observe post facto.
Remark 2. As stated earlier the distributions of this paper are related to other distributions in the literature, but these do not exploit the extreme value connection as we do. For example, when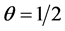
which is a special case, with k = 1, of the generalized half-logistic distribution [5] , eq. 23.83.
Second, the distribution of Z under the CSUG model is a special case of a truncated Pareto distribution, which, for positive a, is defined by
Putting 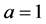
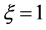
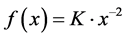
4. Parameter Estimation
The intermingling of polynomial and logarithmic terms makes method of moments estimation difficult in closed form, as in the SUG case. However, if θ is unknown, the maximum likelihood estimate of θ can be found in a satisfying form, both in the CGUG maximum and CSUG minimum cases. Suppose that 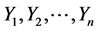
the likelihood function is given by
The MLE of θ is a value of θ, where 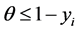
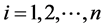
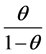
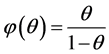
Since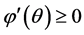
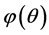
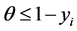
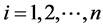
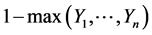
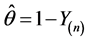
Suppose next that 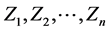
it follows that the likelihood function is given by
As above, it now follows that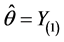
5. A Summary of Some Other Models
The general scheme given by (3) and (4) is quite powerful. As another example, suppose (using the example from Section 1) that
and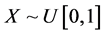
and that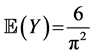
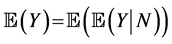
UNIFORM-POISSON MODEL. Here we let 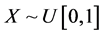
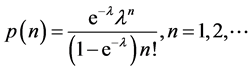
Proposition 5.1. Under the Uniform-Poisson model,
In some sense, the primary motivation of this paper was to produce extreme value distributions that did not fall into the Beta family (such as 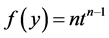
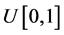
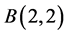
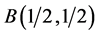
GEOMETRIC-BETA(2, 2) MODEL. Here 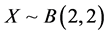
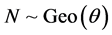
and
POISSON-BETA(2, 2) MODEL. Here 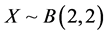
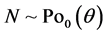
and
GEOMETRIC-ARCSINE MODEL. Here 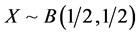
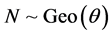
and
POISSON-ARCSINE MODEL. Here 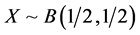
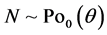
and
GEOMETRIC-TOPP-LEONE MODEL. Here 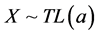
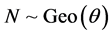
and
POISSON-TOPP-LEONE MODEL. 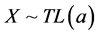
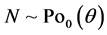
and
6. Conclusion
In this paper we studied a general scheme for the distribution of the maximum or minimum of a random number of i.i.d. random variables with compact support. While some of the distributions obtained through this process have appeared before in the literature, they do not been studied using this approach. Our biggest open problem is to find data sets for which these new distributions are appropriate.
Acknowledgements
The research of AG was supported by NSF Grants 1004624 and 1040928. We thank the referees for their insightful suggestions for improvement.
Cite this paper
Jie Hao,Anant Godbole, (2016) Distribution of the Maximum and Minimum of a Random Number of Bounded Random Variables. Open Journal of Statistics,06,274-285. doi: 10.4236/ojs.2016.62023
References
- 1. Durrett, R. (1991) Probability: Theory and Examples. Wadsworth and Brooks/Cole, Pacific Grove.
http://dx.doi.org/10.4236/am.2012.34054 - 2. Louzada, F., Roman, M. and Cancho, V. (2011) The Complementary Exponential Geometric Distribution: Model, Properties, and a Comparison with Its Counterpart. Computational Statistics and Data Analysis, 55, 2516-2524.
http://dx.doi.org/10.1016/j.csda.2010.09.030 - 3. Louzada, F., Bereta, E. and Franco, M. (2012) On the Distribution of the Minimum or Maximum of a Random Number of i.i.d. Lifetime Random Variables. Applied Mathematics, 3, 350-353.
- 4. Morais, A. and Barreto-Souza, W. (2011) A Compound Class of Weibull and Power Series Distributions. Computational Statistics and Data Analysis, 55, 1410-1425.
- 5. Johnson, N., Kotz, S. and Balakrishnan, N. (1995) Continuous Univariate Distributions. Vol. 2, Wiley, New York.
- 6. Kotz, S. and van Dorp, J. (2004) Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications. World Scientific Publishing Co., Singapore.
http://dx.doi.org/10.1142/5720 - 7. Leadbetter, M., Lindgren, G. and Rootzén, H. (1983) Extremes and Related Properties of Random Sequences and Processes. Springer Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-5449-2 - 8. Earthquake Data Set.
http://www.data.scec.org/eq-catalogs/date_mag_loc.php - 9. Chung, F., Lu, L. and Vu, V. (2003) Eigenvalues of Random Power Law Graphs. Annals of Combinatorics, 7, 21-33.
http://dx.doi.org/10.1007/s000260300002 - 10. Aiello, B., Chung, F. and Lu, L. (2001) A Random Graph Model for Power Law Graphs. Experimental Mathematics, 10, 53-66.
http://dx.doi.org/10.1080/10586458.2001.10504428 - 11. Marshall, A. and Olkin, I. (1997) A New Method of Adding a Parameter to a Family of Distributions with Applications to the Exponential and Weibull Families. Biometrika, 84, 641-652.
http://dx.doi.org/10.1093/biomet/84.3.641 - 12. Kumaraswamy, P. (1980) A Generalized Probability Density Function for Double-Bounded Random Processes. Journal of Hydrology, 46, 79-88.
http://dx.doi.org/10.1016/0022-1694(80)90036-0 - 13. Urzúa, C.M. (2000) A Simple and Efficient Test for Zipf’s Law. Economics Letters, 66, 257-260.
http://dx.doi.org/10.1016/S0165-1765(99)00215-3 - 14. Aban, I.B., Meerschaert, M.M. and Panorska, A.K. (2006) Parameter Estimation for the Truncated Pareto Distribution. Journal of the American Statistical Association, 101, 270-277.
http://dx.doi.org/10.1198/016214505000000411 - 15. Topp, C.W. and Leone, F.C. (1955) A Family of J-Shaped Frequency Functions. Journal of the American Statistical Association, 50, 209-219.
http://dx.doi.org/10.1080/01621459.1955.10501259