Open Journal of Statistics
Vol.05 No.05(2015), Article ID:58584,8 pages
10.4236/ojs.2015.55042
Optimal Generalized Biased Estimator in Linear Regression Model
Sivarajah Arumairajan1,2, Pushpakanthie Wijekoon3
1Postgraduate Institute of Science, University of Peradeniya, Peradeniya, Sri Lanka
2Department of Mathematics and Statistics, Faculty of Science, University of Jaffna, Jaffna, Sri Lanka
3Department of Statistics & Computer Science, Faculty of Science, University of Peradeniya, Peradeniya, Sri Lanka
Email: arumais@gmail.com, pushpaw@pdn.ac.lk
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC- BY-NC).
http://creativecommons.org/licenses/by-nc/4.0/



Received 3 June 2015; accepted 2 August 2015; published 5 August 2015
ABSTRACT
The paper introduces a new biased estimator namely Generalized Optimal Estimator (GOE) in a multiple linear regression when there exists multicollinearity among predictor variables. Stochastic properties of proposed estimator were derived, and the proposed estimator was compared with other existing biased estimators based on sample information in the the Scalar Mean Square Error (SMSE) criterion by using a Monte Carlo simulation study and two numerical illustrations.
Keywords:
Multicollinearity, Biased Estimator, Generalized Optimal Estimator, Scalar Mean Square Error

1. Introduction
To overcome the multicollinearity problem in the linear regression model, several biased estimators were defined in the place of Ordinary Least Squares Estimator (OLSE) to estimate the regression coefficients, and the properties of these were discussed in the literature. Some of these estimators are based on only sample information such as Ridge Estimator (RE) [1] , Almost Unbiased Ridge Estimator (AURE) [2] , Liu Estimator (LE) [3] and Almost Unbiased Liu Estimator (AULE) [4] . However for each case, the researcher has to obtain their properties and to compare the superiority of one estimator over another estimator when selecting a suitable estimator for a practical situation. Therefore [5] proposed a Generalized Unrestricted Estimator (GURE) 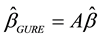 to represent the RE, AURE, LE and AULE, where
to represent the RE, AURE, LE and AULE, where 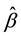 is the OLSE, and A is a positive definite matrix which depends on the corresponding estimators of RE, AURE, LE and AULE.
is the OLSE, and A is a positive definite matrix which depends on the corresponding estimators of RE, AURE, LE and AULE.
However, the researchers are still trying to find the best estimator by changing the matrix A compared to the already proposed estimators based on sample information. Instead of changing A, in this research we introduce a more efficient new biased estimator based on optimal choice of A.
The rest of the paper is organized as follows. The model specification and estimation is given in Section 2. In Section 3, we propose a biased estimator namely Generalized Optimal Estimator (GOE), and we obtain its stochastic properties. In Section 4 we compare the proposed estimator with some biased estimators in the Scalar Mean Square Error criterion by using a real data set and a Monte Carlo simulation. Finally some conclusion remarks are given in Section 5.
2. Model Specification and Estimation
First we consider the multiple linear regression model
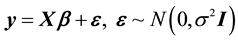 (1)
(1)
where y is an 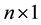 observable random vector, X is an
observable random vector, X is an  known design matrix of rank p,
known design matrix of rank p, 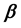 is a
is a 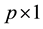 vector of unknown parameters and ε is an
vector of unknown parameters and ε is an  vector of disturbances.
vector of disturbances.
The Ordinary Least Square Estimator of 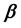 and
and 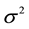 are given by
are given by
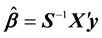 (2)
(2)
and
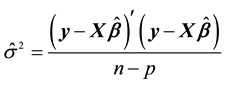 (3)
(3)
respectively, where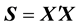 .
.
The Ridge Estimator (RE), Almost Unbiased Ridge Estimator (AURE), Liu Estimator (LE) and Almost Unbiased Liu Estimator (AULE) are some of the biased estimators proposed to solve the multicollinearity problem which are based only on sample information. The estimators are given below:
RE: 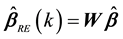 where
where 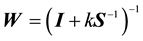 for
for 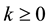
LE: 

AURE: 

AULE: 

Since RE, LE, AURE and AULE are based on OLSE, [5] proposed a generalized form to represent these four estimators, the Generalized Unrestricted Estimator (GURE) which is given as

where 




The bias vector, dispersion matrix and MSE matrix of 


and

respectively.
Instead of changing the matrix 


3. The Proposed Estimator
From (7) the following equation can be obtained by taking trace operator as

By minimizing (8) with respect to


where
Now we can simplify the matrix B as
Therefore

Now we will use the following three results (see [6] , p. 521, 522) to obtain the 

(a) Let M and X be any two matrixes with proper order. Then
(b) If x is an n-vector, y is an m-vector, and C an 
(c) Let x be a K vector, M a symmetric 

By applying (a) we can obtain

Now we consider

By using (b) and (c) we can obtain

and

respectively.
Hence

Substituting (11) and (15) to (9), we can derive that

Equating (16) to a null matrix, we can obtain the optimal matrix 

Note that 

Now we are ready to propose a biased estimator namely Generalized Optimal Estimator (GOE) as

The bias vector, dispersion matrix, mean square error matrix and scalar mean square error of 



and

respectively.
Note that since 





matrix. Now we write the optimal matrix 

Now the bias vector, dispersion matrix, mean square error matrix and scalar mean square error of 



and

respectively.
For practical situations we have to replace the unknown parameters 




4. Numerical Illustration
4.1. Monte Carlo Simulation
To study the behavior of our proposed estimator, we perform the Monte Carlo Simulation study by considering different levels of multicollinearity. Following [7] we generate explanatory variables as follows:
where 


where 












Table 1 can be obtained by using estimated SMSE values obtained by using equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in equation (21) respectively instead of 

According to Table 1, we can say that the GOE-OLSE has the smallest scalar mean square error values with compared to RE, LE, AURE, AULE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE when γ = 0.8, 0.9, 0.99 and 0.999.
4.2. Numerical Example
To further illustrate the behavior of our proposed estimator we consider two data sets. First we consider the data set on Portland cement originally due to [9] . This data set has since then been widely used by many researchers such as [10] - [13] . This data set came from an experimental investigation of the heat evolved during the setting and hardening of Portland cements of varied composition and the dependence of this heat on the percentages of four compounds in the clinkers from which the cement was produced. The four compounds considered by [9] are tricalium aluminate: 3CaO∙Al2O3, tricalcium silicate: 3CaO∙SiO2, tetracalcium aluminaferrite: 4CaO∙Al2O3∙Fe2O3, and beta-dicalcium silicate: 2CaO∙SiO2, which we will denote by



Table 1. Estimated SMSE values of the RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE- AULE when γ = 0.8, 0.9, 0.99 and 0.999.
We assemble our data set in the matrix form as follows:

For this particular data set, we obtain the following results:
a) The eigen values of
b) The condition number = 20.58464
c) The OLSE of 

d) The OLSE of

Table 2 can be obtained by using estimated SMSE values obtained by using Equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in Equation (21) respectively instead of 

From Table 2 we can notice that the GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE have the smallest scalar mean square error value with compared to RE, LE, AURE, AULE. Therefore we can suggest the GOE to estimate the regression coefficients. When k is large, GOE-OLSE has smallest SMSE than GOE-RE. When d is small, GOE-OLSE has smallest SMSE than GOE-LE.
Now we consider the second data set on Total National Research and Development Expenditures as a Percent of Gross National product originally due to [14] , and later considered by [15] - [17] .
Table 2. Estimated SMSE values of RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE- AULE the data set on Portland Cement.
The data set is given below:
The four column of the 10 × 4 matrix 




For this particular data set, we obtain the following results:
a) The eigen values of
b) The condition number = 93.68
c) The OLSE of 
d) The OLSE of

Table 3 can also be obtained by using estimated SMSE values obtained by using Equations (7) and (21) for different shrinkage parameter d or k values selected from the interval (0, 1). The SMSE of GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE are obtained by substituting OLSE, RE, LE, AURE and AULE in Equation (21) respectively instead of 

From Table 3, we can say that our proposed estimator is superior to RE, LE, AURE and AULE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE.
5. Conclusions
In this paper we proposed a new biased estimator namely Generalized Optimal Estimator (GOE) in a multiple linear regression when there exists multicollinearity problem in the independent variables. The proposed estimator is superior to biased estimators which are based on sample information and takes the form
Table 3. Estimated SMSE values of RE, LE, AURE, AULE, GOE-OLSE, GOE-RE, GOE-LE, GOE-AURE and GOE-AULE the data set on total national research and development expenditures.
Acknowledgements
We thank the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing all facilities to do this research.
Cite this paper
SivarajahArumairajan,PushpakanthieWijekoon,11, (2015) Optimal Generalized Biased Estimator in Linear Regression Model. Open Journal of Statistics,05,403-411. doi: 10.4236/ojs.2015.55042
References
- 1. Hoerl, E. and Kennard, W. (1970) Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, 12, 55-67.
http://dx.doi.org/10.1080/00401706.1970.10488634 - 2. Singh. B., Chaubey. Y.P. and Dwivedi, T.D. (1986) An Almost Unbiased Ridge Estimator. Sankhya: The Indian Journal of Statistics B, 48, 342-346.
- 3. Liu, K. (1993) A New Class of Biased Estimate in Linear Regression. Communications in Statistics—Theory and Methods, 22, 393-402.
http://dx.doi.org/10.1080/03610929308831027 - 4. Akdeniz, F. and Kaçiranlar, S. (1995) On the Almost Unbiased Generalized Liu Estimator and Unbiased Estimation of the Bias and MSE. Communications in Statistics—Theory and Methods, 34, 1789-1797.
http://dx.doi.org/10.1080/03610929508831585 - 5. Arumairajan, S. and Wijekoon, P. (2014) Generalized Preliminary Test Stochastic Restricted Estimator in the Linear regression Model. Communication in Statistics—Theory and Methods, In Press.
- 6. Rao, C.R. and Touterburg, H. (1995) Linear Models, Least Squares and Alternatives. Springer Verlag.
http://dx.doi.org/10.1007/978-1-4899-0024-1 - 7. McDonald, G.C. and Galarneau, D.I. (1975) A Monte Carlo Evaluation of some Ridge-Type Estimators. Journal of American Statistical Association, 70, 407-416.
http://dx.doi.org/10.1080/01621459.1975.10479882 - 8. Newhouse, J.P. and Oman, S.D. (1971) An Evaluation of Ridge Estimators. Rand Report, No. R-716-Pr, 1-28.
- 9. Woods, H., Steinour, H.H. and Starke, H.R. (1932) Effect of Composition of Portland Cement on Heat Evolved during Hardening. Industrial and Engineering Chemistry, 24, 1207-1214.
http://dx.doi.org/10.1021/ie50275a002 - 10. Kaciranlar, S., Sakallioglu, S., Akdeniz, F., Styan, G.P.H. and Werner, H.J. (1999) A New Biased Estimator in Linear Regression and a Detailed Analysis of the Widely Analyzed Dataset on Portland Cement. Sankhyā, Ser. B, 61, 443-459.
- 11. Liu, K. (2003) Using Liu-Type Estimator to Combat Collinearity. Communications in Statistics—Theory and Methods, 32, 1009-1020.
http://dx.doi.org/10.1081/STA-120019959 - 12. Yang, H. and Xu, J. (2007) An Alternative Stochastic Restricted Liu Estimator in Linear Regression. Statistical Papers, 50, 639-647.
http://dx.doi.org/10.1007/s00362-007-0102-3 - 13. Sakallioglu, S. and Kaçiranlar, S. (2008) A New Biased Estimator Based on Ridge Estimation. Statistical Papers, 49, 669-689.
http://dx.doi.org/10.1007/s00362-006-0037-0 - 14. Gruber, M.H.J (1998) Improving Efficiency by Shrinkage: The James-Stein and Ridge Regression Estimators. Dekker, Inc., New York.
- 15. Akdeniz, F. and Erol, H. (2003) Mean Squared Error Matrix Comparisons of Some Biased Estimators in Linear Regression. Communication in Statistics—Theory and Methods, 32, 2389-2413.
http://dx.doi.org/10.1081/STA-120025385 - 16. Li, Y. and Yang, H. (2011) Two Kinds of Restricted Modified Estimators in Linear Regression Model. Journal of Applied Statistics, 38, 1447-1454.
http://dx.doi.org/10.1080/02664763.2010.505951 - 17. Alheety, M.I. and Kibria, B.M.G (2013) Modified Liu-Type Estimator Based on (r-k) Class Estimator. Communications in Statistics—Theory and Methods, 42, 304-319.
http://dx.doi.org/10.1080/03610926.2011.577552















