Open Journal of Statistics
Vol.05 No.04(2015), Article ID:56877,6 pages
10.4236/ojs.2015.54030
A Three-Stage Stochastic Dynamic Pricing Game Model Affected by New Products into the Market
Waka Cheung, Fang Chen
Department of Statistics, College of Economics, Jinan University, Guangzhou, China
Email: emailzhj@163.com, 15521332629@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 April 2015; accepted 31 May 2015; published 3 June 2015
ABSTRACT
In real-life marketing, a common phenomenon is that the prices of current product will have been cut down even the new product has not gone into market yet. Thus, it is very important for merchant to set the strategy which can make the excepted revenue maximum. So, this paper constructs a three-stage stochastic dynamic pricing game model for analyzing the influence of the uncertainty of entry timing of the new products on pricing of products being sold. By analyzing of the pricing strategy, there are big differences in the predictions of new product going into market between merchant and customers; the merchant will adopt cutting price for promotion strategy to reduce negative influence of the new products on the demand of the products sold now. Otherwise, the merchant will adopt the strategy of maximizing current period’s profit.
Keywords:
Stochastic Dynamic Pricing Game Model, New Products Entry into Market, Depreciate Sales Promotion Means

1. Introduction
With the development of science and economic technology, dynamic pricing of perishable goods has become a popular research project in academia. Perishable products can be divided into two groups. One has a short validity periods, such as air ticket, movie tickets, foods and so on, thus business’s biggest concern is market clearing. The pricing strategy of these kinds of products has been widely discussed. Another one has a long enough period of validity but updates rapidly, such as 3C product. Their prices will be significantly affected by new products. So, this paper makes perishable products as the research objective. It is important to note that the prices of products sold begin to fall gradually some time before new products going into the market.
In the research about dynamic pricing of perishable goods, [1] from revenue management aspect expounded the dynamic pricing of perishable goods. [2] showed that it is optimal to decrease (resp., to increase) the price as soon as the time-to-go falls below (resp., above) a time threshold that depends on the number of yet unsold items. [3] considered a family of continuous pricing functions, where the optimal pricing strategy can be explicitly characterised and easily implemented. [4] studied the problem of jointly determining the order size and dynamic prices for a perishable inventory system. Owing to the technological change and the volatility of customers’ tastes, the common probabilistic demand model cannot be estimated accurately in practice. Therefore, when the demand is a hybrid uncertainty, the optimal strategy for perishable goods can be obtained in [5] . Based on [5] , [6] applied the Hamilton-Jacobi-Bellman (HJB) equation to discuss the dynamic pricing when the products demand is a stochastic variable and the discounted criterion is included.
As the time going on, compared with the current products in the market, the potential products will be into market so that a demand transfers between potential products and current products. To solve this problem, [7] proposed a concept about “demand distraction” which constructs a bridge between new product and current product. To consider the discount principles situation, [8] constructed a Cournot game model which describes the influence of transfer probability to the balance result. Five years ago, [9] modeled Cournot competition as a stochastic dynamic game and the optimization algorithm for decision making is proposed. However, in those researches time is not as a divisor in pricing research and the time is a very importance factor in product pricing.
So this paper carries the time as a stochastic variable, and under this condition, the optimal strategy is discussed. In this problem, it is assumed that merchant knows time distribution of new products which will be launched in next 3 periods, while customers have no information on the time of the new products. Merchant can transfer the demand of next phase into current consumption by depreciating. Sales promotion means to reduce negative influence of the new products on the demand of the products sold now. Based on those assumptions, a stochastic dynamic pricing game model is constructed. Then we get the conclusion, that is to say, if the probability of launching new products next phase is less than or equal to a marginal value, merchant will not carry out promotion tactics. If the probability is greater than the marginal value, merchant will not implement promotional strategies until lunching new products.
2. The Model and Main Results
2.1. The Model Construction
In the market of a product, there exists one merchant and multiple customers. Besides the products on sale, there is one potential new product coming in the market. However, no one knows its exact time of entering. Before the new product entering into market, the demand function of the product on sale is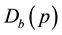 . After the new product entering into market, the demand function of the product on sale is
. After the new product entering into market, the demand function of the product on sale is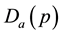 , where a market price is p. We assume that
, where a market price is p. We assume that
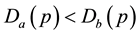 and
and . For the merchants, denoting the purchase price as
. For the merchants, denoting the purchase price as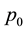 , which is not affected by the new product into market.
, which is not affected by the new product into market.
Thus, before the new product entering into market, the profit function is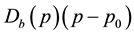 . After the new product entering into market, the profit function is
. After the new product entering into market, the profit function is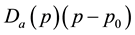 . Let both of these two profit functions be concave functions with respect to p. If we want to only maximize the profit of current period, before the new product entering into market, merchant’s maximum profit should satisfy
. Let both of these two profit functions be concave functions with respect to p. If we want to only maximize the profit of current period, before the new product entering into market, merchant’s maximum profit should satisfy
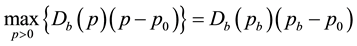 (1)
(1)
where
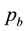 is the price for the maximum profit. After the new product entering into market, merchant’s maximum profit should satisfy
is the price for the maximum profit. After the new product entering into market, merchant’s maximum profit should satisfy
 (2)
(2)
where
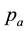 is the price for the maximum profit.
is the price for the maximum profit.
Lemma 1: 1) merchant’s maximum profit before the new product into market should be larger than merchant’s maximum profit after the new product going into market.
2)

Proof: 1)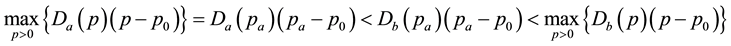 (3)
(3)
2)
 is the price for the maximum profit and the profit function is a concave function. Therefore,
is the price for the maximum profit and the profit function is a concave function. Therefore,
 satisfy first-order condition:
satisfy first-order condition:
 (4)
(4)
Similarly,


Due to that



Since the profit function is concave function and its derivative function is monotonic decreasing function, we can obtain

Table 1 shows all stages of decision tree denoted by the position




From Table 1, the new product has not gone into market yet in period 1 and in period 2, the new product maybe has gone into market or maybe not. However, the new product must go into market in period 3.
In practice, the information acquitted by merchants is usually different from customers, which means that merchants and customers would have different prediction about the new product’s time to market. Therefore, we make the following assumptions in this paper:
Assumption 1: In period 1, merchant does not know whether the new product goes into market in period 2, but knows the probability, which is
Assumption 2: In period 1, customers do not know whether the new product goes into market in period 2, but knows the probability, which is
In each period, the merchant firstly make the decision of sale price. In period 1 and period 2, the merchant have two strategies to chose. The first strategy maximizes the profit of current period and the merchant will give the price according to the first strategy. The second strategy reduces the sale price to attract customers to buy the products for the demand of next period. Assuming that customers’ purchase behaviors ahead of one period happen, the merchant will give the price to maximize the profit sum of current period and next period. In the final period, the merchant does not have the cross-period goal. What the merchant has is the strategy maximizing the profit of current period.
In each period, customers will make the consumption decision when they see the price provided by the merchant. In period 1 and period 2, customers have two strategy choices. One is to purchase the demand goods of current periods. Another is cross-period purchase strategy, which means that customers purchase the demand goods of current and next periods at the same time. To simplify the model, we assume that customers do not have cross-period purchase strategy.
2.2. The Main Results and Proof
In the following, inverses induction method will be used to derive the sub-game refining solutions in three-stage
Table 1. Merchant’s decision tree.
game. It is assumed that the merchant adopts the strategy of maximizing the profit of current period in period 1: the merchant set the price of current period to maximize the current period’s profit. Since the new product does not go into market, the merchant’s maximum profit can be shown as (1).
The following period 2 has two stages. The first stage stands for the new product to market in position (1, 2). Under this condition, the merchant has two strategies, i.e., maximizing current period’s profit and cutting price for promotion. Since the new product has gone into market, the merchant’s maximum profit can be seen as (2) if the merchant adopts the strategy of maximizing the current period’s profit. In final period, the merchant only has the strategy of maximizing the current period’s profit and his profit is also (2). In other words, if the merchant adopts the strategy of maximizing the current period’s profit in the position (1, 2), profit sum of the final two periods can be written as

For the merchant, another strategy in the position (1, 2) is cutting price to promote. We assume that customers have cross-period purchase behavior. If customers purchase goods in current period but do not use until the next period, each product costs c for the preservation cost. If customers think that they can purchase



Since customers know that the new product has gone into market, the demand of customers is




where the current demand quantity is



Since the profit (7) is larger than (8), the merchant will adopt the strategy of maximizing the current period’s profit.
The second stage shows that in the position (2, 2) the new product has not gone into market. Under this condition, the merchant has two strategies, i.e., maximizing current period’s profit and cutting price for promotion. If the merchant adopts the strategy of maximizing current period’s profit in the position (2, 2), his maximum profit is (1). In the final period, the merchant can only use the strategy of maximizing current period’s profit and his maximum profit is (2).
In other words, if the merchant adopts the strategy of maximizing current period’s profit in the position (2, 2), the excepted profit sum of the final two periods is

For the merchant, another strategy in the position is cutting price. Similar to the above analysis, since the customers know the new profit goes into market in period 3, their demand quantity in period 3 is


Since the profit (9) is larger than (10), the merchant will adopt the strategy of maximizing the current period’s profit in the position (2, 2).
To sum up, if the merchant adopts the strategy of maximizing the current period’s profit in period 1, he will adopt the strategy of maximizing the current period’s profit in the final two periods no matter whether the new product appears in period 2. The merchant’s profits are (7) and (9), respectively. In period 1, since the merchant knows the probability of new product to market in period 2 is

Equation (11) is the meaning of profit sum under the assumption that the merchant adopts the strategy of maximizing the current period’s profit in period 1. In the following, the meaning of profit sum will be analyzed on the condition that the merchant adopts cutting price strategy in period 1. Owing to new product has not gone into market in period 1, there exists two possible equilibrium price in period 2 if the merchant does not adopt cross-period strategy in period 1. That is to say the price of product on sale is






where the current demand quantity is



Considering the price problem of current product in period 2, regardless of whether the new product coming to market or not, if the merchant adopts the strategy of maximizing current period’s profit, the profit of current periods is zero. The reason is that the demand of period 2 has been purchased in period 1. Thanks to the last period, the merchant only has the strategy of maximizing the current period’s profit and his profit is (2), so his profit sum of the final two periods can be written as

Another strategy in period 2 is that slashing prices to improve the demand. In this situation customers has knew that the new product has gone into market, the demand of customers and the price of product on sale are



Since the profit (13) is larger than (15), the merchant will adopt the strategy of maximizing the current period’s profit in period 2. Thus, if the merchant adopts cutting price for promotion strategy in period 1, the merchant will adopt the strategy of maximizing the current period’s profit in period 2, his expected profit sum of the whole periods can be written as

We discuss the next problem is that which strategy can be selected by merchant in period 1, either maximizing current period’s profit or cutting price for promotion. When the merchant adopt two strategies, his expected profit sum of the whole periods are (11) and (15). At this moment, if the profit (11) is larger than (15), the merchant will adopt the strategy of maximizing the current period’s profit. On the other hand, if the profit (15) is greater than or equal to (11), the merchant will adopt cutting price for promotion strategy.
That’s to say profit (11) > (15) is equal to

Profit (15) ≥ (11) is equal to

where
In conclusion, according to the inverses induction method analysis, the sub-game refining solutions in three- stage game were obtained.
Proposition 1: the sub-game refining solutions in three-stage game are as follows:
1) If (16) is formed, the merchant will adopt the strategy of maximizing the current period’s profit in each period and the customer is to purchase the demand goods of current periods.
2) If (17) is formed, the merchant will adopt cutting price for promotion strategy in period 1 and will adopt the strategy of maximizing the current period’s profit in the final two periods .In such circumstances, the customers will purchase the demand products of the two former periods in period 1and purchase the demand products of current period in period 3.
In the following, the proposition 1 will be used to find the reason why the merchant adopts cutting price for promotion strategy in period 1 and the regularity will be found when (17) is correct.
Assumption 3: let

where the inequality (18) is a special situation about (17) when the condition satisfy




Corollary 1: As with the assumption 3 is correct, the merchant will adopt cutting price for promotion strategy in period 1 when the merchant predicts the probability of new product does go into market is sufficient lager and the customer forecast the probability of new product does go into market is sufficient small in period 2.
Proof: Owing to the inequality (18) is a special situation about (17) when the condition satisfies






Why do merchant carry out depreciate sales promotion in period 1 when there are big differences in the predictions of launching new products between customers and them? When customer expects the probability of new products launched in next period is low, he would think that the price of products sold now in next period will be similar to the current price. If merchant slash the price, the customers advance their future demand to current consumption. On the contrary, while customer expects the probability of new products launched in next period is great, he would think that the price of products sold now in next period will be lower, thus business has to cut prices deeply to attract customers to consume their future demand.
On the other hand, when merchant expects there is very probability of new products launching in next period, he thinks the profits in next period will be less than this period. So, he will attract customers to consume their future demand now by slashing price to reduce negative influence of the new products on the demand of the products sold now.
3. Conclusions
This paper constructs a three-stage stochastic dynamic pricing game model, and offers a motive of the businesses in cutting prices strategy. Because merchants know more about the new products than the customers, the probability of new products launched in next period they predicts will be greater than their customers. The conclusion is that if there are big differences [see Proposition 1] in the predictions of launching new products between merchant and customers, merchant will attract customers to consume their future demand now by slashing price to reduce negative influence of the new products on the demand of the products sold now.
In general, this paper carries the time as a stochastic variable and the optimal strategy is given, which is most practical for the merchants. And it makes the market economy and real life meaningful.
References
- Weatherford, R. and Bodily, S. (1992) A Taxonomy and Research Overview of Perishable Asset Revenue Management: Yield Management, Overbooking and Pricing. Operations Research, 10, 831-844. http://dx.doi.org/10.1287/opre.40.5.831
- Feng, Y. and Gallego, G. (1995) Optimal Starting Times for End-of-Season Sales and Optimal Stopping Times for Promotional Fares. Management Science, 41, 1371-1391. http://dx.doi.org/10.1287/mnsc.41.8.1371
- Anjos, M.F., Cheng, R.C.H. and Currie, C.S.M. (2005) Optimal Pricing Policies for Perishable Products. European Journal of Operational Research, 166, 246-254. http://dx.doi.org/10.1016/j.ejor.2004.02.015
- You, P.S. and Chen, T.C. (2007) Dynamic Pricing of Seasonal Goods with Spot and Forward Purchase Demands. Computers and Mathematics with Applications, 54, 490-498. http://dx.doi.org/10.1016/j.camwa.2007.01.026
- Li, G.D., Xiong, Z.K., Zhou, Y. and Xiong, Y. (2013) Dynamic Pricing for Perishable Products with the Hybrid Uncertainty in Demand. Applied Mathematics and Computation, 219, 10366-10377. http://dx.doi.org/10.1016/j.amc.2013.04.008
- Cao, P., Li, J.B. and Yan, H. (2012) Optimal Dynamic Pricing of Inventories with Stochastic Demand and Discounted Criterion. Operations Research, 217, 580-588. http://dx.doi.org/10.1016/j.ejor.2011.09.048
- Luo, L., Yu, Y.B. and Liu, D.W. (2006) Optimal Pricing Policies of Perishable Products with Demand Transfer. Journal of Industrial Engineering and Engineering Management, 20, 38-42.
- Yang, H. and Zhou, J. (2006) A Cournot Game of Setting Optimal Markdown Timing for Perishable Products. Chinese Journal of Management Science, 14, 46-50.
- Hamed, K. and Ashkan, R.K. (2011) Decision Making in Dynamic Stochastic Cournot Games. Mathematics and Computers in Simulation, 81, 1202-1217. http://dx.doi.org/10.1016/j.matcom.2010.11.007


