Open Journal of Statistics
Vol.05 No.02(2015), Article ID:55814,2 pages
10.4236/ojs.2015.52017
A Note on the Characterization of Zero-Inflated Poisson Model
G. Nanjundan, Sadiq Pasha
Department of Statistics, Bangalore University, Bangalore, India
Email: nanzundan@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 March 2015; accepted 16 April 2015; published 20 April 2015
ABSTRACT
Zero-Inflated Poisson model has found a wide variety of applications in recent years in statistical analyses of count data, especially in count regression models. Zero-Inflated Poisson model is characterized in this paper through a linear differential equation satisfied by its probability generating function [1] [2] .
Keywords:
Zero-Inflated Poisson Model, Probability Generating Function, Linear Differential Equation

1. Introduction
A random variable X is said to have a zero-inflated Poisson distribution if its probability mass function is given by
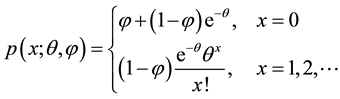 (1)
(1)
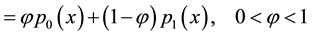
where 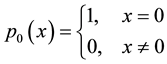 and
and
 ,
,  ,
,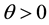 .
.
Thus, the distribution of X is a mixture of a distribution degenerate at zero and a Poisson distribution with mean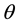 .
.
2. Probability Generating Function
The probability generating function (pgf) of X is given by

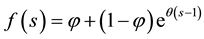 .
.
3. Characterization
Let X be a non-negative integer valued random variable with  and the pgf
and the pgf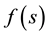 . Then, the distribution of X is zero-inflated Poisson if and only if
. Then, the distribution of X is zero-inflated Poisson if and only if , where
, where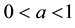 , b are constants and
, b are constants and 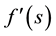 is the first derivative of
is the first derivative of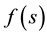 .
.
Proof:
1) Suppose that X has a zero-inflated Poisson distribution specified in (1.1). Then the pgf of X is given by
On differentiation, we get

Hence 

2) Suppose that the pgf 
If





Therefore
3) The Linear Differential Equation
The linear differential equation 
where 


Then its solution is given by

where c is an arbitrary constant.
Here

Hence

Therefore the solution of the Equation (2) is given by

We now extract the probabilities

Since 



We get



Now,
Since

We have
with 

Therefore X has the pgf specified in Equation (1).
References
- Nanjundan, G. (2011) A Characterization of the Members of a Subfamily of Power Series Distributions. Applied mathematics, 2, 750-751. http://dx.doi.org/10.4236/am.2011.26099
- Nanjundan, G. and Ravindra Naika, T. (2012) An Asymptotic Comparison of the Maximum Likelihood and the Moment Estimators in a Zero-Inflated Poisson Model. Applied mathematics, 3, 610-617. http://dx.doi.org/10.4236/am.2012.36095









