Open Journal of Statistics
Vol.05 No.01(2015), Article ID:53860,4 pages
10.4236/ojs.2015.51006
Statistical Significance of Geographic Heterogeneity Measures in Spatial Epidemiologic Studies
Min Lian1,2
1Department of Medicine, Washington University School of Medicine, St. Louis, Missouri, USA
2Alvin J. Siteman Cancer Center, Barnes-Jewish Hospital and Washington University School of Medicine, St. Louis, Missouri, USA
Email: mlian@wustl.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 January 2015; accepted 3 February 2015; published 6 February 2015
ABSTRACT
Assessing geographic variations in health events is one of the major tasks in spatial epidemiologic studies. Geographic variation in a health event can be estimated using the neighborhood-level variance that is derived from a generalized mixed linear model or a Bayesian spatial hierarchical model. Two novel heterogeneity measures, including median odds ratio and interquartile odds ratio, have been developed to quantify the magnitude of geographic variations and facilitate the data interpretation. However, the statistical significance of geographic heterogeneity measures was in- accurately estimated in previous epidemiologic studies that reported two-sided 95% confidence intervals based on standard error of the variance or 95% credible intervals with a range from 2.5th to 97.5th percentiles of the Bayesian posterior distribution. Given the mathematical algorithms of heterogeneity measures, the statistical significance of geographic variation should be evaluated using a one-tailed P value. Therefore, previous studies using two-tailed 95% confidence intervals based on a standard error of the variance may have underestimated the geographic variation in events of their interest and those using 95% Bayesian credible intervals may need to re-evaluate the geographic variation of their study outcomes.
Keywords:
Spatial Epidemiology, Heterogeneity, Statistical Significance, 95% Confidence Interval, 95% Credible Interval

1. Introduction
Spatial epidemiology is an important methodology to deal with spatial-correlated issues in epidemiologic studies. One of its core tasks is to determine geographic variations and quantify the magnitude of geographic variations in diseases, health behaviors, or environmental exposures [1] . Some published epidemiologic studies inappropriately estimated the statistical significance of geographic heterogeneity measures of examined events.
The generalized linear mixed model and the Bayesian spatial hierarchical model are the most commonly applied to fit the data with a multilevel spatial structure. A geographic variation can be directly quantified as neighborhood-level variance 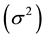 from parameter estimations of the multilevel model fitting. However, this variance has no meaningful unit and is difficult to interpret. Spatial statisticians and epidemiologists have developed two state-of-the-art heterogeneity measures, the median odds ratio (MOR, Equation (1)) [2] - [4] and the interquartile odds ratio (IqOR, Equation (2)) [5] , to facilitate the interpretation of geographic heterogeneity of an event.
from parameter estimations of the multilevel model fitting. However, this variance has no meaningful unit and is difficult to interpret. Spatial statisticians and epidemiologists have developed two state-of-the-art heterogeneity measures, the median odds ratio (MOR, Equation (1)) [2] - [4] and the interquartile odds ratio (IqOR, Equation (2)) [5] , to facilitate the interpretation of geographic heterogeneity of an event.
 (1)
(1)
where 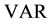 is the neighborhood-level variance, while
is the neighborhood-level variance, while 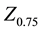 is the
is the 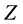 value of the Gaussian distribution at the 75th percentile (0.6745).
value of the Gaussian distribution at the 75th percentile (0.6745).
 (2)
(2)
where 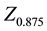 and
and 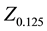 are the
are the 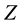 values of the Gaussian distribution at the 87.5th and 12.5th percentiles (1.1504, −1.1504), respectively.
values of the Gaussian distribution at the 87.5th and 12.5th percentiles (1.1504, −1.1504), respectively.
Both MOR and IqOR are derived from the variance and are always greater than or equal to one. Larger values of MOR and IqOR denote greater geographic variations in the event of interest. The MOR reflects the average difference of risk when comparing two subjects who have the same individual characteristics and are selected randomly from two different neighborhoods. The IqOR represents the average difference of risk when comparing the first quartile of study subjects residing in neighborhoods with the highest risk to the fourth quartile of study subjects residing in neighborhoods with the lowest risk [3] [5] . Similarly, the median rate ratio (MRR) and the interquartile rate ratio (IqRR) can be estimated in a prospective study, and the median hazards ratio (MHR) and the interquartile hazard ratio (IqHR) [6] are for time-to-event studies. To facilitate the explanation, the MOR and IqOR are applied in the following discussions.
2. Issues in Determining the Statistical Significance of Geographic Heterogeneity Measures
Geographic variations can be qualitatively assessed by using neighborhood-level variance estimation derived from a generalized linear mixed model. The modeling conducted by a commonly used statistical analysis package, such as the SAS, also gives a Z value and a corresponding P value based on an approximately normal distribution of the estimated parameter. With the standard error of the variance from the multilevel model fitting, a 95% CI is able to be computed mathematically. However, one cannot perform a generalized linear mixed analysis to estimate the statistical significance and 95% CIs of the MOR and IqOR because both MOR and IqOR are derived from the variance and do not have their own standard errors.
Alternatively, a Bayesian spatial hierarchical model with a Markov Chain Monte Carlo (MCMC) simulation has been used to estimate geographic heterogeneities. In this setting, the 95% Bayesian credible interval (CrI), defined by the 2.5th and 97.5th percentiles of Bayesian posterior distribution of the geographic heterogeneity measure, has been commonly reported.
In the estimation of a fixed effect of an exposure, its statistical significance can be identified if the 95% confidence/credible interval of its regression coefficient does not cross zero. However, this empirical method conflicts with the nature of geographic heterogeneity measures. Two unreasonable results are usually reported in the studies in which the 95% CI or CrI of geographic heterogeneity measures were used to determine their statistical significance. The 95% CI of the variance could cross zero based on an approximately normal distribution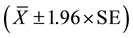 . This is unreasonable because the variance should always be greater than or equal to 0. In addition, the 2.5th percentile of the Bayesian posterior distribution of the variance is always greater than 0 and consequently the MOR and IqOR are always greater than one. This leads to the overestimation of geographic disparities.
. This is unreasonable because the variance should always be greater than or equal to 0. In addition, the 2.5th percentile of the Bayesian posterior distribution of the variance is always greater than 0 and consequently the MOR and IqOR are always greater than one. This leads to the overestimation of geographic disparities.
3. Example and Solution
3.1. Example
A simulation analysis was performed to illustrate the issues relevant to the statistical significance of spatial heterogeneity measures. It is assumed that a population of colorectal cancer (CRC) survivors come randomly from 100 neighborhoods, each with 5 - 20 patients, and that the probability of smoking for each patient is 0.2 - 0.5. A random simulation generated a dataset that included 1245 patients and 420 smokers. Multilevel logistic regression is applied to quantify small-area geographic variation in smoking behavior among these CRC patients (Equation (3)).
 (3)
(3)
where 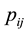 is the probability of smoking for patient
is the probability of smoking for patient  who resides in neighborhood
who resides in neighborhood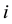 ;
; 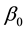 is the intercept;
is the intercept; 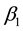 and
and 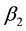
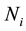
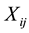
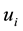

To simplify the explanation, an empty model without neighborhood- and individual-level covariates was fit to estimate the overall geographic heterogeneity of smoking among these CRC patients using the Bayesian hierarchical approach with a MCMC simulation in WinBUGS (Version 1.4.3, MRC, UK). After 50,000 iterations for the convergence, additional 50,000 iterations were run to obtain the posterior estimates of three spatial heterogeneity measures. Because the dataset was simulated randomly, the geographic variation in smoking was expected to be small.
Table 1 shows the Bayesian parameter estimates of three heterogeneity measures. Based on an approximately normal assumption, the 95% CIs of three geographic measures were computed as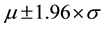
3.2. Solution
Table 2 shows that, the variance is a non-negative measure, and MOR and IqOR are never less than one. The null hypothesis of the statistical test should be that the variance equals to zero and both MOR and IqOR equal to one, that is, there is no significant geographic variation in the event of interest. Meanwhile, the alternative hypothesis of the statistical test should be that the variance is greater than zero, and both MOR and IqOR are greater than one. Therefore, the statistical test is theoretically one-tailed, rather than two-tailed. The critical value for the significance level at 0.05 is 1.645 instead of 1.960. The statistical significance should be denoted directly using one-tailed (right-tailed) P value. One may not report the 95% CI or the interval between the 2.5th
Table 1. Three Bayesian estimates of three spatial heterogeneity measures in the simulated example.
*VAR, variance; †MOR, median odds ratio; ‡IqOR, interquartile odds ratio.
Table 2. Three spatial heterogeneity measures and their statistical hypotheses.
*VAR, variance; †MOR, median odds ratio; ‡IqOR, interquartile odds ratio.
and the 97.5th percentiles of Bayesian posterior distribution (95% CrI) of geographic heterogeneity measures to avoid the misinterpretation of geographic variations. In fact, a one-tailed P value for the variation/heterogeneity estimation has been given from a generalized linear mixed model fitting using common statistical analysis packages, such as the SAS. For the heterogeneity estimation from a Bayesian hierarchical model, one should compute the corresponding statistics, based on the prior distribution of the variance, to obtain their one-tailed P value to determine its statistical significance. In the simulated example, since the Z value for the variance is: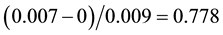
4. Discussions
The purpose of this study was to point out an inappropriate method that was used to determine the statistical significance of geographic heterogeneity measures. The simulated data suggested that empirically reporting of the 95% CI/CrI of geographic heterogeneity measures may lead to misunderstanding of the statistical significance of geographic variations of an event.
According to the nature of geographic heterogeneity measures, the statistical inference should be one-tailed (right-tailed). It is inappropriate to report a two-tailed 95% CI/CrI of a heterogeneity measure in spatial epidemiologic studies. It could mislead one in understanding the statistical significances of heterogeneity measures. In the studies using standard errors to obtain two-tailed P values or 95% CIs, geographic variations in the events may be underestimated because a two-tailed test is more conservative than a one-tailed test. In contrast, the studies using the interval between the 2.5th and the 97.5th percentiles of a Bayesian posterior distribution to obtain a 95% CrI may overestimate the statistical significance of geographic variation of the event because a Bayesian 95% CrI never crosses zero for the variance and one for both MOR and IqOR. The issue of statistical significance of geographic heterogeneity measures, which was discussed in this paper, is also extendible to a general multilevel study aiming to investigate the variation(s) in one or multiple event(s) of interest across a non-spatial higher level, such as healthcare providers or medical service facilities.
Acknowledgements
This work is supported partly by a Career Development Award (K07 CA178331) and a Research Award (R21 CA169807) funded by the National Cancer Institute, and a Research Award (R01 AA021492) funded by the National Institute of Alcohol Abuse and Alcoholism, both at the National Institutes of Health. I also thank the service provided by the Health Behavior, Communication and Outreach Core, which is supported by the National Cancer Institute Cancer Center Support grant (P30 CA091842) awarded to the Alvin J. Siteman Cancer Center at Barnes-Jewish Hospital and Washington University School of Medicine. I declare no conflict of interest.
References
- Elliott, P. and Wartenberg, D. (2004) Spatial Epidemiology: Current Approaches and Future Challenges. Environmental Health Perspectives, 112, 998-1006. http://dx.doi.org/10.1289/ehp.6735
- Larsen, K., Petersen, J.H., Budtz-Jorgensen, E. and Endahl, L. (2000) Interpreting Parameters in the Logistic Regression Model with Random Effects. Biometrics, 56, 909-914. http://dx.doi.org/10.1111/j.0006-341X.2000.00909.x
- Larsen, K. and Merlo, J. (2005) Appropriate Assessment of Neighborhood Effects on Individual Health: Integrating Random and Fixed Effects in Multilevel Logistic Regression. American Journal of Epidemiology, 161, 81-88. http://dx.doi.org/10.1093/aje/kwi017
- Merlo, J., Chaix, B., Ohlsson, H., Beckman, A., Johnell, K., Hjerpe, P., Rastam, L. and Larsen, K. (2006) A Brief Conceptual Tutorial of Multilevel Analysis in Social Epidemiology: Using Measures of Clustering in Multilevel Logistic Regression to Investigate Contextual Phenomena. Journal of Epidemiology and Community Health, 60, 290-297. http://dx.doi.org/10.1136/jech.2004.029454
- Chaix, B., Merlo, J., Subramanian, S.V., Lynch, J. and Chauvin, P. (2005) Comparison of a Spatial Perspective with the Multilevel Analytical Approach in Neighborhood Studies: The Case of Mental and Behavioral Disorders Due to Psychoactive Substance Use in Malmo, Sweden, 2001. American Journal of Epidemiology, 162, 171-182. http://dx.doi.org/10.1093/aje/kwi175
- Chaix, B., Rosvall, M. and Merlo, J. (2007) Assessment of the Magnitude of Geographical Variations and Socioeconomic Contextual Effects on Ischaemic Heart Disease Mortality: A Multilevel Survival Analysis of a Large Swedish Cohort. Journal of Epidemiology and Community Health, 61, 349-355. http://dx.doi.org/10.1136/jech.2006.047597
Abbreviations and Acronyms
VAR: variance;
MOR: median odds ratio;
MRR: median rate ratio;
MHR: median hazard ratio;
IqOR: interquartile odds ratio;
IqRR: interquartile rate ratio;
IqHR: interquartile hazard ratio.


