Received 6 August 2014; revised 9 September 2014; accepted 28 September 2014

ABSTRACT

It is well known that the number of people with Tuberculosis (TB) and those who develop multi- drug resistance (MDR) are the fundamental components that affect the total cost of treatment of TB. This paper has two-fold objectives. Firstly, we use the Generalized Linear Regression Models (GLM) to predict the future count of persons with TB and MDR. Due to the fact that assessment of TB cost is methodologically difficult, and compounded with the lack of concrete information about the treatment cost in Saudi Arabia, our second objective is to use cost information from the EU countries as proxy to estimate the cost of treating TB. The cost predictions provide essential information that is part of the evidence needed for budgeting and financing the health care facilities of TB services, especially with respect to avoiding under-estimation of the cost of TB-MDR treatment.

Keywords:

Infectious Diseases, Negative Binomial Model, TB Cost, MDR

1. Introduction

Tuberculosis (TB) has remerged as a threat to global health and is considered to be the second most common cause of death due to infectious diseases after HIV/AIDS (Human Immunodeficiency Virus/Acquired Immunodeficiency Syndrome) globally. In 2012, approximately 8.6 million new TB cases and 1.3 million TB-related deaths were reported including 0.17 million death due to multi drug resistance TB [1] . It has been evidenced that majority of the TB related deaths are reported from low and middle income countries [1] . The largest number of cases was reported from Asia (58%), and Africa (27%). Smaller proportions were reported from the Eastern Mediterranean Region (8%), European Region (4%) and The Americas (3%). The five countries that rank first to fifth in terms of total numbers of incident cases in 2012 are India (1.6 - 2.4 million), China (1.0 - 1.6 million), South Africa (0.38 - 0.57 million), Indonesia (0.34 - 0.52 million) and Pakistan (0.42 - 0.60 million). India and China alone accounted for an estimated 38% of TB cases worldwide [1] . However, prevalence and mortality rates appear to be falling in all the six regions reported by [1] .

Disturbingly, there were an estimated 450,000 cases of multidrug-resistant TB (MDR-TB) in 2012 with an estimated 170,000 deaths [1] . Overall 3.6% of newly diagnosed and 20% of the previously treated cases had MDRTB. Globally, 92 countries had reported cases of extensively drug-resistant tuberculosis (XDR-TB) by the end of 2012 [1] . These last figures are reason for considerable concern and highlight a potential threat to our ability to treat tuberculosis, both in individual patients and in the context of a treatment program [2] .

According to the WHO the incidence of TB all forms, smear positive TB and deaths from TB each rose by 6.2% between 1990 and 2004, but the prevalence declined. These figures suggest that the notification rates of TB in Saudi Arabia increased during this period, as did the successful treatment rate, such that a decrease in the total number of cases was seen at the same time as the incidence and death rates increased [1] [2] . Despite the noticeable improvements on notification and successful treatment rates yet Saudi Arabia has a moderate infection rate in comparison with the other countries [3] . Figure 1 shows the TB incidence from 1992 to 2010. Note the sharp decline in the incidence starting from 2000, which may be attributed to the control measures (regulations related to mandatory TB testing, treatment protocol, and hospitalization of TB MDR patients) imposed by the country’s Ministry of Health (MOH).

In the Kingdom of Saudi Arabia, there are up to nine million migrants mainly from TB endemic regions, in South/South East Asia and Africa. In addition, annually 3 - 6 million pilgrims are visiting the holy cities located in the western region of the Kingdom for performing the holy rituals, Hajj and Umrah. Interestingly, the majority of these pilgrims are coming from TB endemic areas of Asia and Africa. There are differences in the rate of TB infection between different regions of the country. For instance in Jeddah (sea and air ports for pilgrims) the infection rate can reach up to 64 cases per 100,000 compared with 32 per 100,000 in Riyadh (Central). The higher rate in Jeddah may be attributed to the inflow of pilgrims.

The published data depict that TB in Saudi Arabia is still not fully controlled despite the huge efforts exerted by the MOH under the National TB Programs to eradicate the disease even with the implementation of Direct Observed Therapy (DOTS). However in the last 10 years, the mortality rates among TB patients in the country showed a decreasing trend (7.2% to 6.1%) among Saudis and a steady trend among non-Saudis [3] . A distribution of the number of TB cases by province over the years 2000-2009 in KSA was given in Table 6 of reference [3] . A graphical representation of the data is given Figure 2.

From the available data we would like to build a prediction model to provide projections for the future burden of the disease in KSA. This model may help public health officials determine the most appropriate intervention strategy to reduce the burden of diseases. The immediate benefits that can be gained from this predictive model are:

・ With the extraneous available cost data, the model helps in evaluating the economic burden for TB and MDR treatments. We shall develop a reliable model, with high prediction accuracy to predict the TB counts in KSA.

・ Many TB patients may develop Multi-Drug-Resistance (MDR) and this would substantially increase the cost of therapy. Predicting the MDR fraction of patients from the total TB count is required to provide a more credible estimate of the economic burden of the disease.

The most likely major cost saving for TB treatment is the reduction in MDR admissions [4] , hence reducing the risk of hospital admission, and avoiding toxicity resulting from giving higher doses to patients.

This paper is structured as follows: In Section 2 we use the data published in [3] to build a time series fixed effect model from which we predict future counts of TB cases. In Section 3 we analyze the EU cost data published in [5] and establish a relationship between cost of treatment, the number of TB cases and the Gross Domestic Product (GDP) of each country, and in Section 4 we combine the results obtained from Sections 3 and 4 to predict the treatment cost of both TB and MDR cases. A general discussion will be taken up in Section 5.

2. TB Counts Prediction: Generalized Linear Regression Models

The data presented in Figure 2, prevalence data in each province given in [3] show the trend over time. From Figure 2, there seems to be a clustering of the data in three sub-groups. The first is Makkah, the second is the Riyadh Region and all other regions constituted as a third cluster. Regardless of this apparent sub-group clustering, the natural physical grouping of the data in the 7 regions will be kept in-tact, and regions will be explicitly included as 6 fixed covariates in the proposed modeling strategy. The available data are presented as time series of counts. Variability over time and region (province) must be accounted for in the process of building a predictive model. Unlike most regression techniques, time series methods acknowledge the correlation structure of the data. For surveillance data which are generally collected monthly, or yearly the principal correlations are auto- correlations at a lag of one time period, or serial correlation [6] . When time series data are available over a relatively long period of time, it is important to estimate the trend and seasonal components as the auto-correlation structure can only be identified by using a stationary time series. Failure to account properly for the auto-corre- lation will result in a miss-specified model which may have bias in the estimated effects and prediction intervals which are too narrow.

A major attraction of longitudinal data is the ability to control for all stable covariates, without actually including them in a regression equation. In general, this is accomplished by using only within-regional variation to estimate the parameters, and then averaging the estimates over regions. Regression models for accomplishing this are often called fixed-effects models [7] [8] .

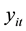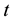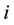
Fixed-effects have been developed for a variety of different data types and models, including the Poisson regression models for count data [7] . The fixed-effects Poisson regression model for longitudinal data has been described in detail by Cameron et al. [9] . Let the dependent variable denote the TB count at time for region 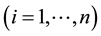and over time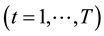. It is assumed that 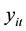to have a Poisson distribution with parameter 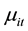which, in turn, depends on a vector of exogenous variables 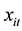according to the log-linear link function [9] :

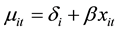(1)

One way to estimate the parameter of this model is to do conventional Poisson regression by maximum likelihood, including dummy variables for all 7 regions (less one) to directly estimate the fixed effects.

For Poisson regression, two estimation methods―unconditional maximization of the likelihood and conditional likelihood―always yield identical estimates for 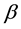and the associated covariance matrix [9] . For the fixed-effects Poisson regression model we have the restriction that the mean of each count must equal its variance:

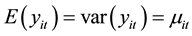(2)

The probability distribution of 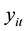is given by:

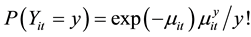(3)

In many data sets, however there may be additional heterogeneity not accounted for by the model. A potential problem with our data is that there is still some evidence of over-dispersion in the data. Substantial departures from the mean variance ratio could indicate a problem with the model specification, and also suggest that the estimated standard errors may be downwardly biased.

One way to deal with the problem of over-dispersion is to alternatively assume that has a negative binomial distribution (NBD), which can be regarded as a generalization of the Poisson distribution with an additional parameter (dispersion parameter) allowing the variance to exceed the mean [9] . The probability distribution of NBD is given by:

(4)

The parameter is assumed to be constant over time for each region or province depends on covariates through the transformation:

(5)

The mean and variance of are given by

(6)

Therefore, when, the NB distribution reduces to the Poisson distribution. For the time series regional data graphed in Figure 2, we have two fixed effects, the year, and the province. Therefore the parameters vector has three components. We use dummy variables for the fixed effects representing regions, and a continuous covariate representing time, we fitted the count data with both models using the SAS software V9.3. Results of fitting the Poisson and NB regression models are summarized in Table 1. The goodness of fit measure is the scaled deviance. The closer the scaled deviance to 1, the better the fit is. The Akaike Information Criterion (AIC) may also be used as measure of goodness of fit as well (the smaller the AIC the better the fit is). The p-value is summary statement of the omnibus test that, the data follow the underlined model. A small p-value indicates that the Poisson model is not supported by the data. Clearly the NB is superior to the Poisson model.

The NB fitted equation, under the log-link is given by:

(7)

where

^*Northern territory includes North, Tabuk, and Al-Jouf. Southern territory includes Aseer, Jizan, Naran, and Al-Baha. The Makkah Region is the reference.

For example the predicted count in Makkah in the year 2020 is:

All covariates are significant with p-value < 0.0001.

For a model to be used as predictive tool, the observed counts should be as close as possible to the model based predictive counts. This basically is the concept of goodness-of-fit, which also means that the model has to be internally valid. The Pearson’s Chi-square is often used for this purpose. However, this test is affected by one or two discrepancies between observed and expected counts, even if the rest of the expected counts are quite close to their corresponding observed counts. We alternatively use the Concordance Correlation Coefficient (CCC) [10] to assess the goodness of fit of the NBM, or its internal validity. The CCC is given by:

(8)

and are respectively the standard deviations of the observed and the NB predicted counts, and is the Pearson’s correlation between the two sets of counts. The observed and predicted totals are depicted in Table 2.

Direct computation from the data in Table 3 gives. This high value of the CCC confirms the high reproducibility of the model as a predicting tool.

Based on the NBM, the projections from the year 2011 to 2020 are given in the following Table 3.

3. Statistical Analysis of Cost of Treating TB in the EU

The main objective of this section is to review and summarize the available evidence on the global cost and the cost components of TB and MDR in the EU countries [5] . Comparing cost of illness studies is difficult because of the different definitions and methods used to measure and quantify cost, whether direct or indirect. The scope of the indirect cost measurement varies considerably across studies: some only include economically active individuals, but others include children and the elderly; most measure the time spent seeking treatment by the patient and caregiver and their loss of productive labor time due to illness.

Diel et al. [5] performed a systematic literature review, followed by the extraction of direct as well as indirect costs of TB. Direct costs include costs for the medical treatment of TB (medication, laboratory, hospitalization and outpatient visits) and indirect costs represent productivity loss because of TB?induced sick days off?work. They gathered information on several cost components based on data available in the year 2012:

1) Duration of hospitalization and inpatient cost per day.

2) Outpatient cost.

3) Cost of medication.

4) Cost due to loss of productivity.

5) Year in which the costs were assessed or collected.

The authors of [5] recognized the limitation of the review. Nevertheless, despite the limitations, the best available cost data are part of the evidence needed for budgeting and financing the expansion of TB services, especially with respect to scaling-up MDR-TB treatment. In their review, the authors emphasize the fact that lack of sufficient information from many countries makes extrapolation a necessity.

It should be noted that the recent WHO global tuberculosis report [11] data may be utilized to identify the major factors that affect the total cost levels. These are the total TB count and cost of treatment, percentage of MDR and its treatment cost. In reviewing the literature on cost of treating TB, we discovered that there is a wide variation in allocation of treatment cost that is attributed mainly to the annual household income. To strengthen the analysis we augmented the data with information regarding the Gross Domestic Product [12] of each country in the data base.

Our proposed cost estimation proceeded in three steps:

1) In the first step, we split the EU countries into two groups. The first group included the founding nations of the EU, and this includes 16 countries (Austria, Belgium, Cyprus, Denmark, Finland, France, Germany, Greece, Ireland, Italy, Luxemburg, Malta, Portugal, Spain, Sweden, and UK). The second group includes countries that joined the union at later dates, and this group included 10 countries (Bulgaria, Czeck R. Estonia, Hungary, Latvia, Lithuania, Poland, Romania, Slovakia, Slovenia), most of which were the former Eastern-Bloc Nations. To evaluate the accuracy of the grouping, we used the ROC to classify the EU nations into two categories using as a predictor. The ROC curve is given in Figure 3.

The area under the AUC is 0.956 ± 0.036 (p-value < 0.00001), and the cut-off point is US $24,800. At this point the sensitivity and specificity of our classification scheme were given respectively as 76% and 80%. The coefficient of agreement “kappa” between the observed and the predicted classifications was 78%, which according to the benchmarks set by Landis and Koch [13] is substantial.

2) In Table 4, we produced some relevant summary statistics for the two groups. The two groups differ significantly with respect to the GDP/per capita and the log-cost of treatment per TB case. Thereafter we looked at the relationship between the total cost of treating TB and the number of TB cases. It is evident from Figure 4 evident, which is the scatter plot of the cost of treatment and the number of TB cases, that there is a quadratic relationship between the total cost and the number of TB cases (Figure 4). When we fitted a quadratic regression model to the data, the relationship is given Equation (8).

(8)

In (8) TB is the total count in 2011 The percent of explained variation in total cost that attributed to the total number of TB cases is measured by, indicating an excellent fit.

In an interesting review [14] it was reported that there is a significant relationship between the treatment cost per TB case and the annual household income, a variable that is not measured in the data base that we are analyzing from [5] . However, we may use the GDP as a proxy variable [15] to predict the cost of treatment. Proxy variables are occasionally used in econometric analysis when important independent predictors are not available. We attempted to model the relationship between cost of treatment per TB case and the GDP as a proxy variable, but the relationship was not statistically significant. However, when we dichotomized the GDP at the cut-off vale $24,900, as mentioned earlier, we created two classes of countries, thereafter. Using this categorical variable as a predictor, we were able to establish a statistically significant relationship between the country-class and the cost per TB case on the log scale. This approach may be controversial, but we claim that this is a case of zero-causal effect but positive predictive comparison between the two classes of countries [15] - [17] . This regression equation is given in (9)

, (9)

where country class = 1, if a country belongs to the first 16 nations, and zero otherwise. The negative value of the regression coefficient means that the group of countries in class = 1 have on the average lower cost of treatment per TB case, relative to the other 10 countries in the sample.

4. Cost Prediction in KSA

Since the EU cost data are for the year 2011, the projected number of TB cases in 2011 in KSA, based on the NBM is 4171. It has been reported that the GDP in KSA is 29,600 US. This means that KSA belongs to country- class = 1.

Therefore the estimated total cost of TB in KSA in 2011

.

This is a baseline cost, and it in be adjusted upward to offset the effect of inflation, or downward if a cheaper drugs are available.

On the other hand, from the EU data [5] the relationship between the total cost of treatment of MDR-TB is linearly related to the number of MDR-TB cases (scatter plot is Figure 5). The regression equation is:

(10)

The fitted equation is excellent since the.

Now, if the percentage of MDR in KSA in 2011 was 0.045, this means that the projected number of MDR-TB cases in KSA is MDR cases.

The projected cost due to MDR in KSA is therefore expected to be:

.

This means, on average MDR cost per case, while a TB-case costs .

The above calculations show that although MDR-TB is a small fraction of the total TB cases, it consumes a huge proportion of the total budget allocated for the treatment of TB. It is therefore aids the policy makers in their disease management strategy.

5. Discussion

Despite declining global TB incidence, this infectious disease remains a major public health issue, particularly in KSA. What exacerbates the problem is the large number of migrant workers who come from countries with high TB burden. In several EU countries where there was a low incidence of TB, the rate of decline had slowed down [18] . Drug resistance and HIV co-infection are the main factors affecting the trend [19] . From the regression analysis of the EU cost data, we found that the total cost of treating TB was a quadratic function of the TB count. Therefore a reliable estimate of TB count is needed in order to accurately estimate the total treatment cost, moreover the reliability of the prediction would definitely improve when we use longer time series data. The NBM was proved to be a good predicting tool with and its goodness of fit to the data was excellent. Because we lacked information about the treatment cost in KSA, we relied on the published EU cost data and the GDP of the EU countries to establish a relationship between the cost-per TB case and the GDP-dependent class category of the country, and from this relationship we produced a base-line estimate of the total cost of TB treatment in KSA. This algorithm has two limitations. Firstly, the cost structure, as reported in the meta-analysis paper [5] , varies from one country to the other, even within the EU countries, and naturally this variation should encompass KSA. The second is related to the use of proxy information in the prediction process. This approach has theoretical challenges that could not be discussed in this paper.

Acknowledgements

The authors acknowledge the constructive comments made by two anonymous reviewers.

References

NOTES

^*Corresponding author.