Open Journal of Statistics
Vol.3 No.6A(2013), Article ID:41371,8 pages DOI:10.4236/ojs.2013.36A006
Inference Based on Empirical Likelihood for Varying Coefficient Model with Random Effect
1College of Applied Sciences, Beijing University of Technology, Beijing, China
2Department of Mathematics, Yancheng Teachers University, Yancheng, China
Email: lwb@emails.bjut.edu.cn, lgxue@bjut.edu.cn
Copyright © 2013 Wanbin Li, Liugen Xue. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Wanbin Li, Liugen Xue. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received November 14, 2013; revised December 14, 2013; accepted December 21, 2013
Keywords: Varying Coefficient Model; Random Effect; Empirical Likelihood; Longitudinal Data
ABSTRACT
In this article, we develop a statistical inference technique for the unknown coefficient functions in the varying coefficient model with random effect. A residual-adjusted block empirical likelihood (RABEL) method is suggested to investigate the model by taking the within-subject correlation into account. Due to the residual adjustment, the proposed RABEL is asymptotically chi-squared distribution. We illustrate the large sample performance of the proposed method via Monte Carlo simulations and a real data application.
1. Introduction
Varying coefficient model has been widely used to model all kinds of data. One popular application is the analysis of the longitudinal data (e.g. [1,2]). Although both [3] and [4] proposed effective inference procedure for the varying coefficient model and applied them to the analysis of CD4 count data, whose detailed information can be referred to [5], none of them considered the within-subject correlation of longitudinal data. To improve the efficiency of the inference by considering this kind of correlation, we consider the varying coefficient model with random effect
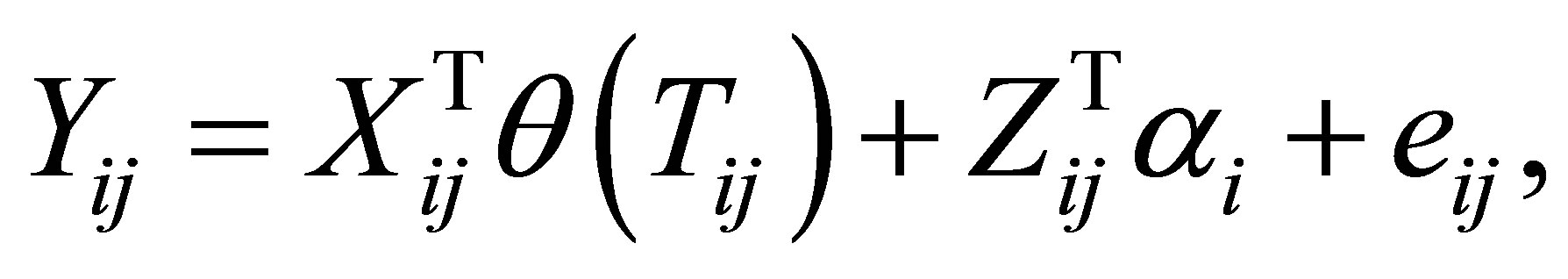 (1)
(1)
with  where
where  is an unknown smoothing
is an unknown smoothing 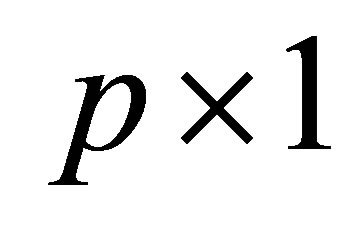 function vector,
function vector,  are independent
are independent  vectors of random effect with mean 0 and covariance matrix D and
vectors of random effect with mean 0 and covariance matrix D and  are independent mean 0 random variables with variance
are independent mean 0 random variables with variance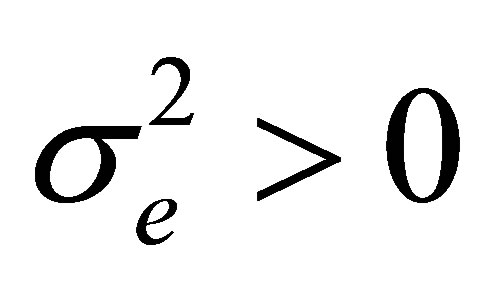 . Let
. Let 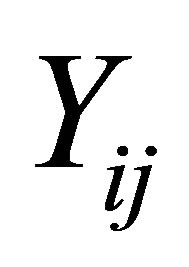 and
and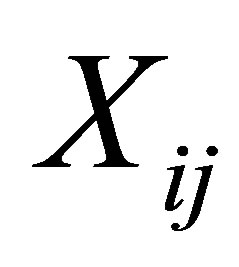 ,
,  ,
, 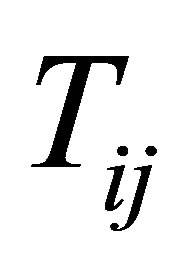 denote the response and covariate variable, respecttively, where the i and j are their associated jth measurement of the ith subject among all of the longitudinal data.
denote the response and covariate variable, respecttively, where the i and j are their associated jth measurement of the ith subject among all of the longitudinal data.
Random effect model is frequently employed to exploit the characteristics of longitudinal data over several time periods. Recently, there has been fruitful research on it. (e.g. [6-9]) proposed an efficient estimation for the single index model with random effect and provided a further way to construct the confidence interval for the parameter of interest with the aid of an estimator for its asymptotic variance.
In this article, we address a general problem to construct the confidence interval for the varying coefficient model with random effect by using the empirical likelyhood method (e.g. [10-12]). Thanks to the empirical likelihood method, we can construct the confidence interval without the estimation for the asymptotic variance, and the whole inference procedure is totally data-adaptive. For longitudinal data, except for [3,13] studied an empirical likelihood method for the varying coefficient error-in-variable models with longitudinal data. Both of them did not consider incorporating the within-subject correlation. [14] reported that it caused a loss of efficiency for empirical likelihood applications by ignoring the within-subject correlation. In this article, we propose a residual-adjusted block empirical likelihood (RABEL) method for the varying coefficient model with random effect to incorporate the within-subject correlation for longitudinal data. This approach is appealing in that it can not only construct the confidence interval for the unknown coefficient function, but also improve estimation efficiency through considering the within-subject correlation of longitudinal data. Also the estimation procedure introduced in Section 2 makes the implementation much easier.
The rest of this article is organized as follows. In Section 2, we introduce the residual-adjusted block empirical likelihood method and provide details on constructing the confidence interval for the varying coefficient function of interest. Some asymptotic results are derived in Section 3 and several implementation issues are shown in Section 4. Simulations are reported in Section 5. Data arising from CD4 study is analyzed in Section 6. Proofs of the main results are relegated to Appendix.
2. Estimation Method
2.1. Empirical Likelihood Estimation
Assume that the observed data 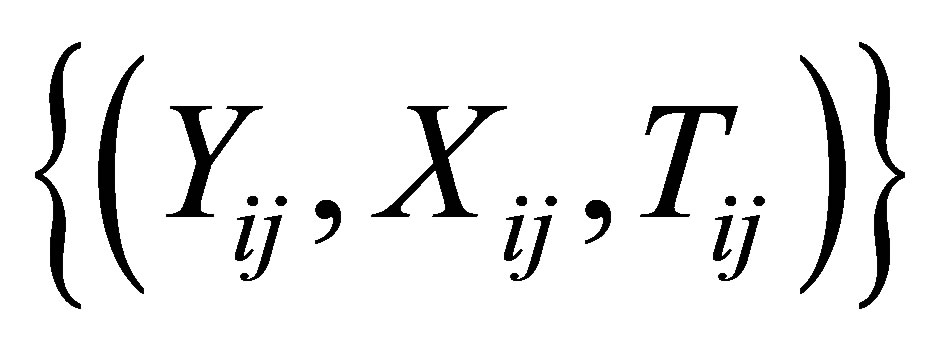 are generated from model (1). Moreover, let
are generated from model (1). Moreover, let ,
, 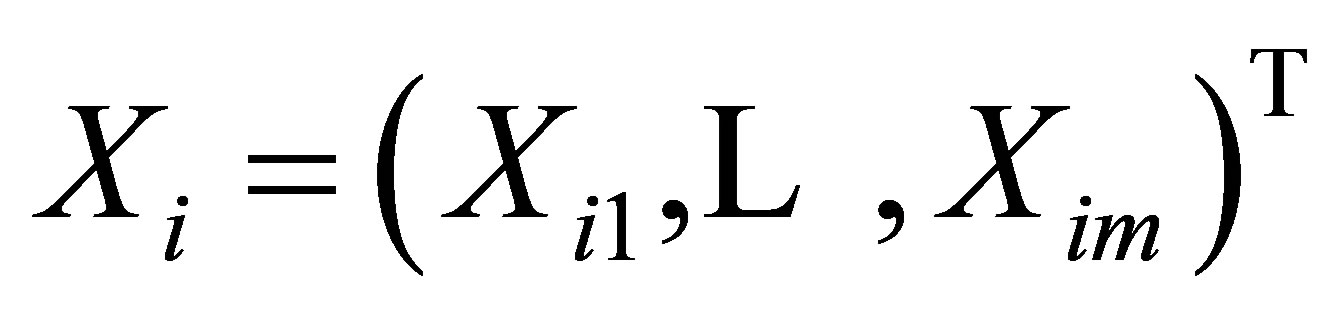 ,
, 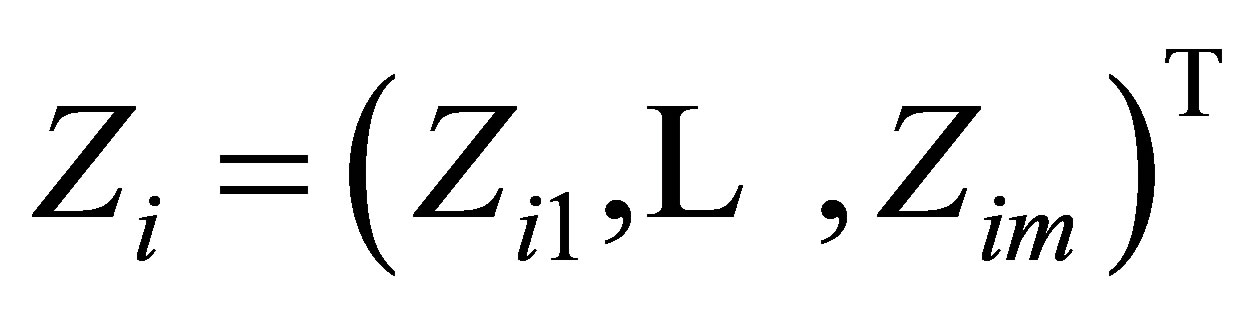 and
and  . Based on the idea of GEE [15], we can construct an auxiliary random vector nonparametric component
. Based on the idea of GEE [15], we can construct an auxiliary random vector nonparametric component
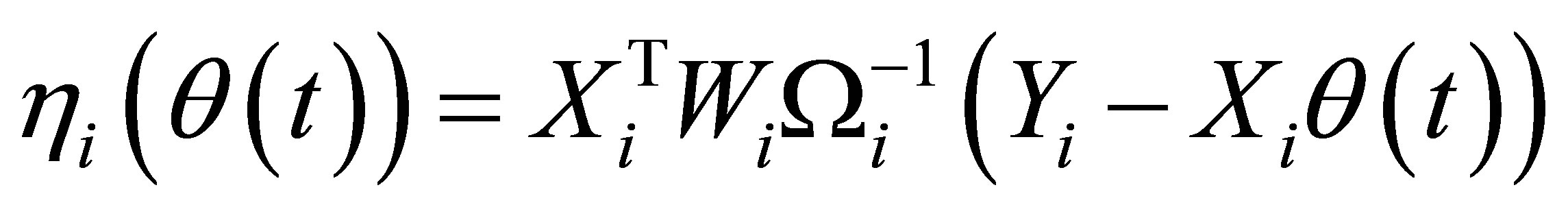 (2)
(2)
where 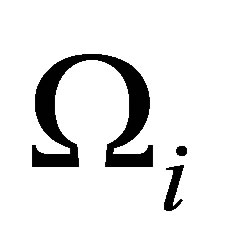 is the within-subject covariance matrix. Denote
is the within-subject covariance matrix. Denote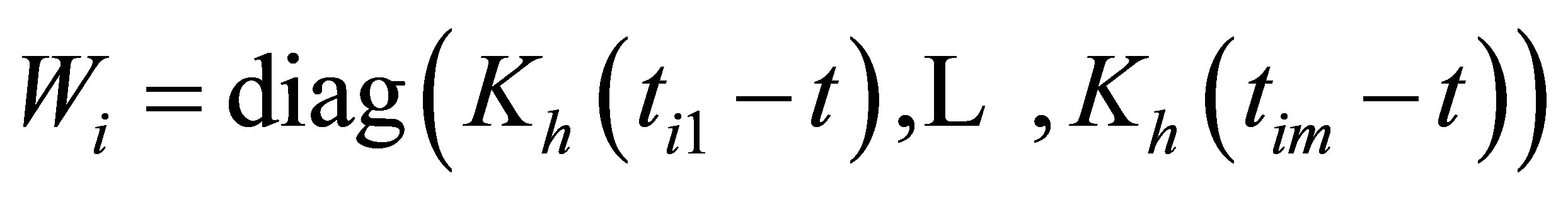 , where
, where  with
with 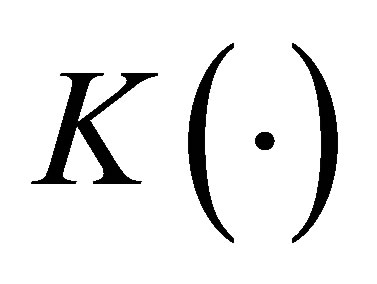 and
and  being a kernel function and proper bandwidth, respectively. Note that
being a kernel function and proper bandwidth, respectively. Note that 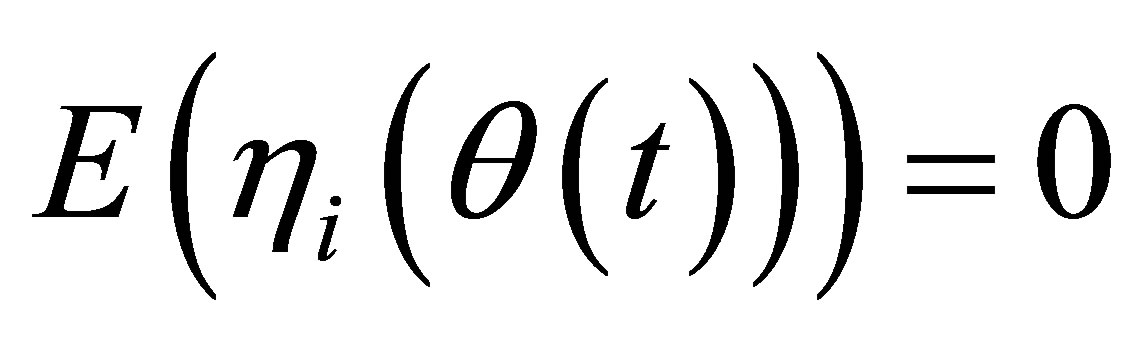 if
if 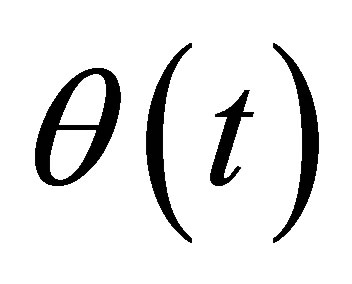 is the true parameter. Therefore, we can introduce an estimating equation as
is the true parameter. Therefore, we can introduce an estimating equation as
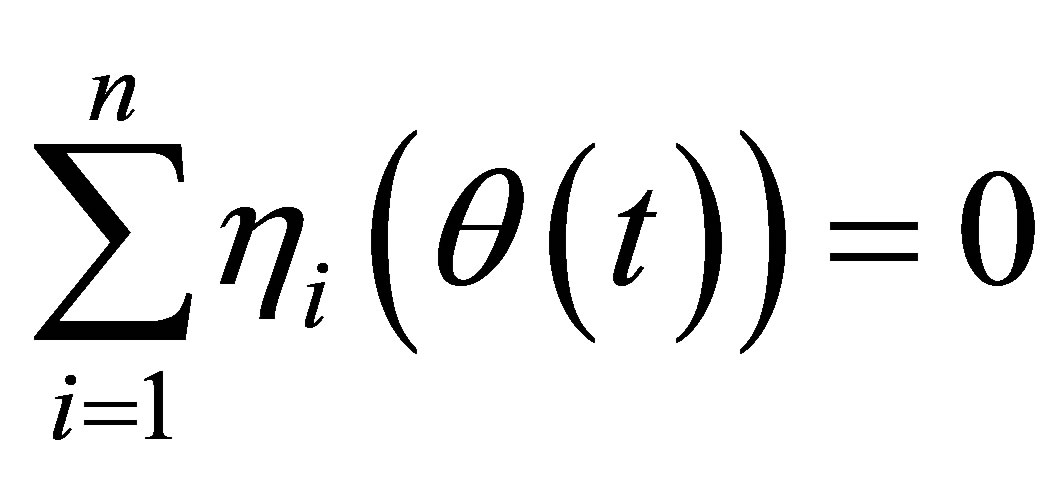 , and a naive empirical log-likelihood ratio function for
, and a naive empirical log-likelihood ratio function for 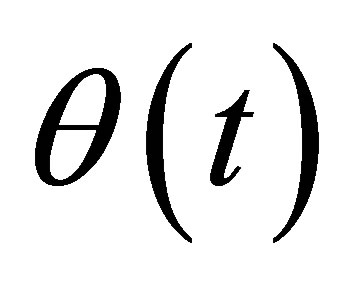 can be derived as
can be derived as
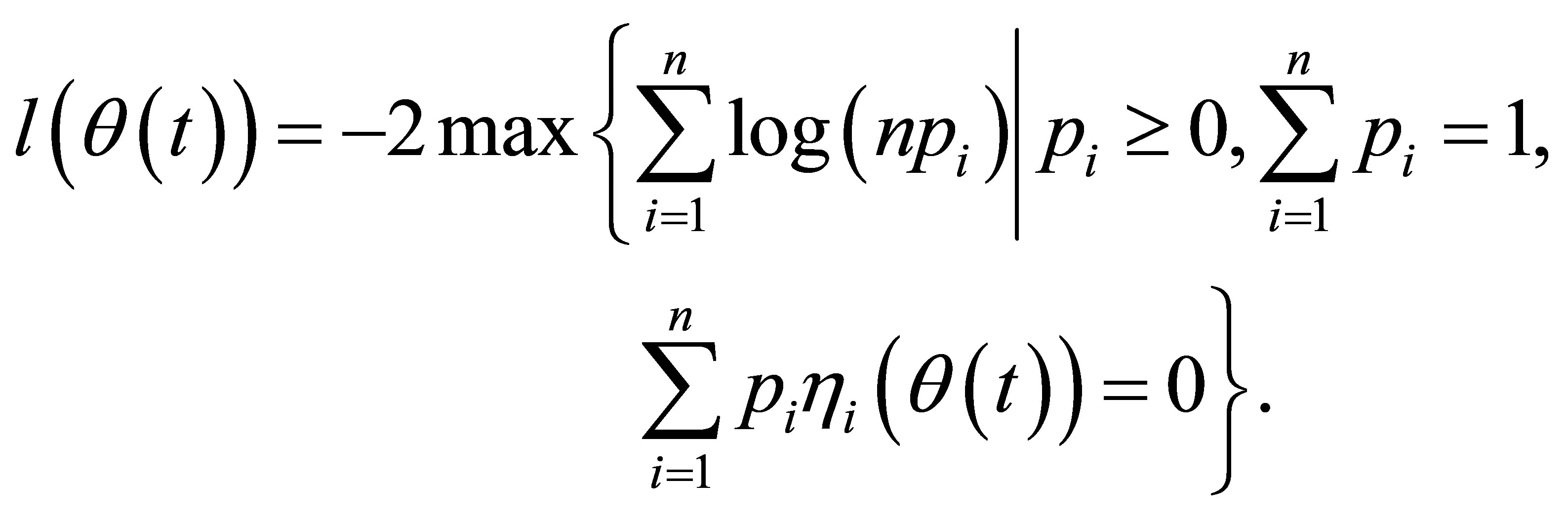 (3)
(3)
However, by the similar argument in [3], the proposed empirical log-likelihood ratio (3) is no longer a standard chi-square distribution unless an undersmoothing bandwidth is chosen. And some complicated techniques, such as Monte Carlo approximation or estimated transformation, have to be employed to make further inference. For its limit being chi-square in practice, we propose a RABEL method by taking the ideal of [14] and [16]. Under the framework of RABEL, the auxiliary random vector function is newly defined as
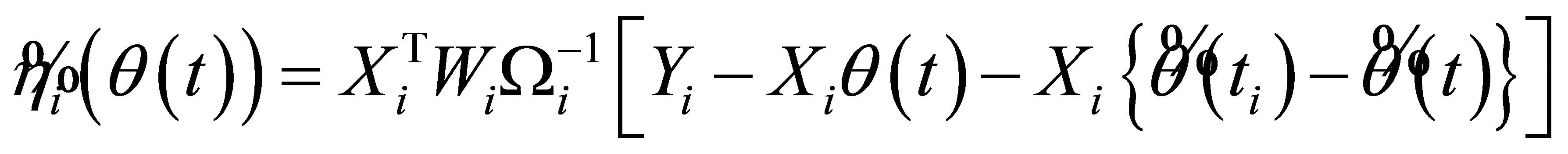 (4)
(4)
where the estimator  is a preliminary estimator. And the RABEL ratio is further derived as
is a preliminary estimator. And the RABEL ratio is further derived as
 (5)
(5)
By the Lagrange multiplier method, we have
 (6)
(6)
where  is a
is a 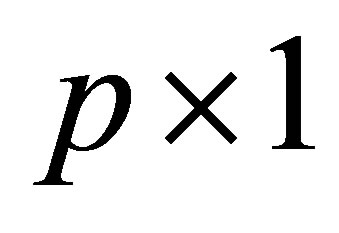 vector satisfying
vector satisfying
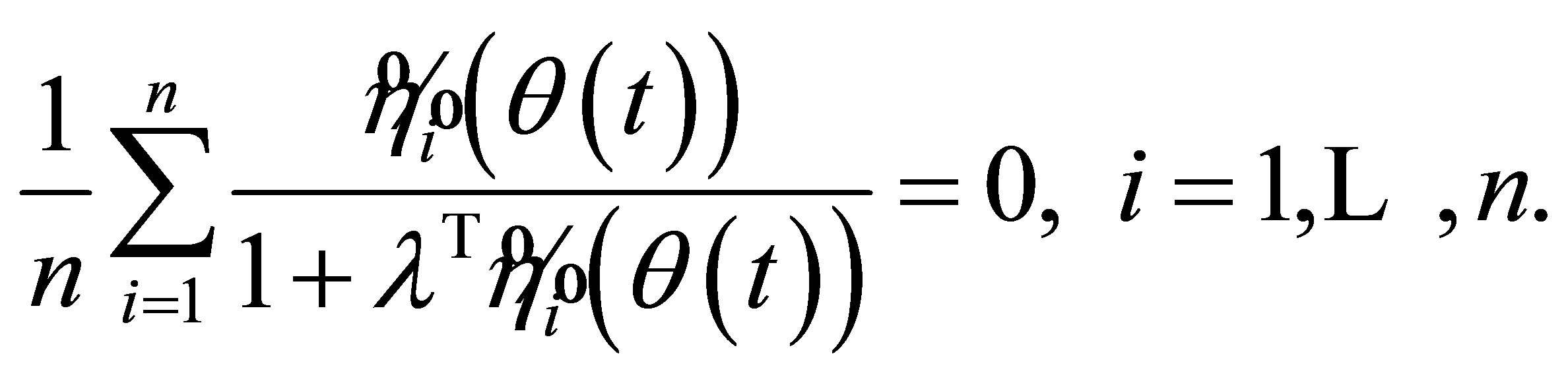 (7)
(7)
Then, the empirical likelihood ratio function (5) can be represented as
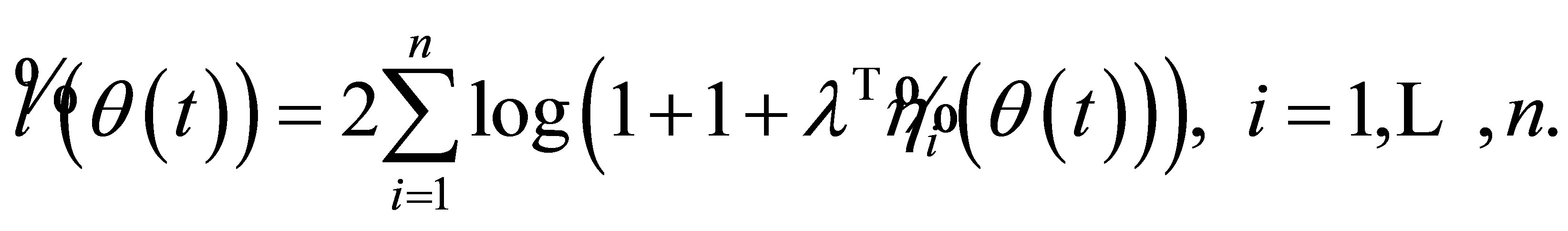 (8)
(8)
2.2. Estimation of the Variance Component
The within-subject covariance 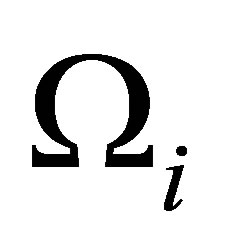 is assumed to be known in the proposed RABEL procedure in Section 2.1. However, in practice, we need to construct an estimator for it. Assume that the model (1) satisfies the variance covariance-variance model
is assumed to be known in the proposed RABEL procedure in Section 2.1. However, in practice, we need to construct an estimator for it. Assume that the model (1) satisfies the variance covariance-variance model
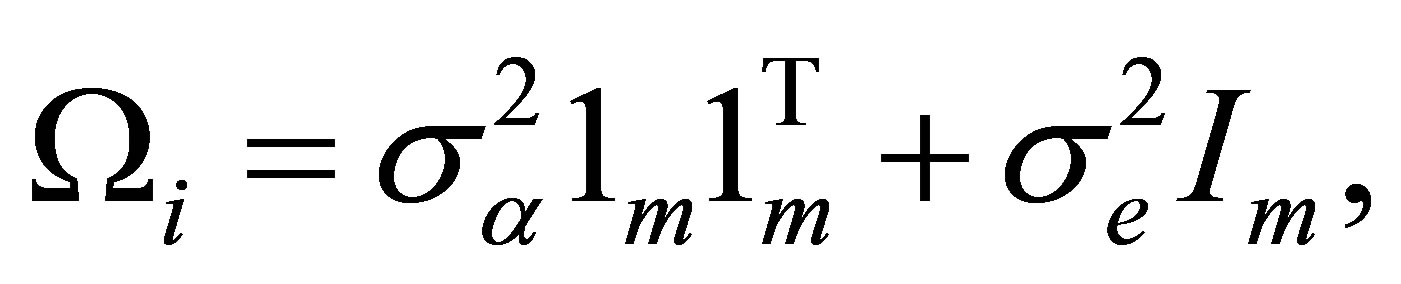 (9)
(9)
where  represents an
represents an  vector of ones and
vector of ones and 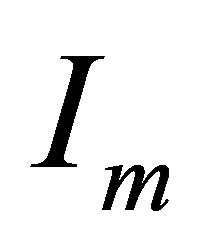 is the
is the 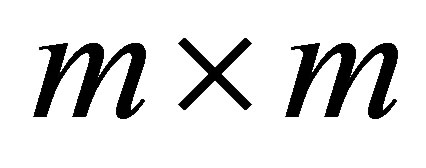 identity matrix. This proposed model (9) is called a variance component model and widely used in longitudinal analysis, see, for example (e.g. [8,9]). Let
identity matrix. This proposed model (9) is called a variance component model and widely used in longitudinal analysis, see, for example (e.g. [8,9]). Let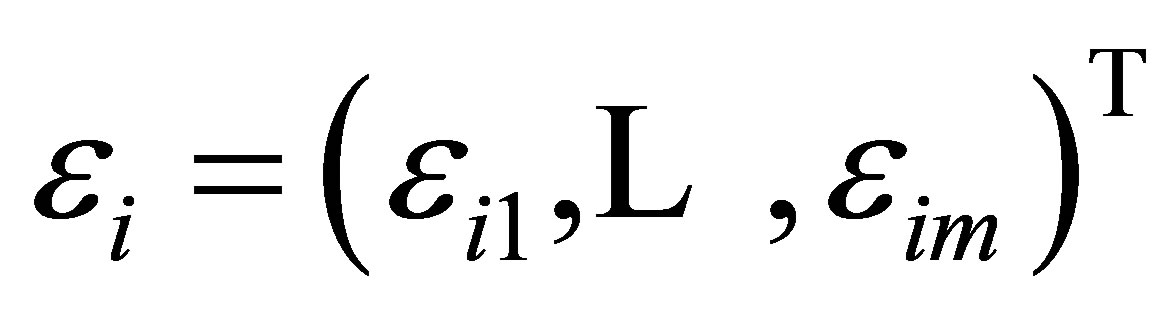 , with
, with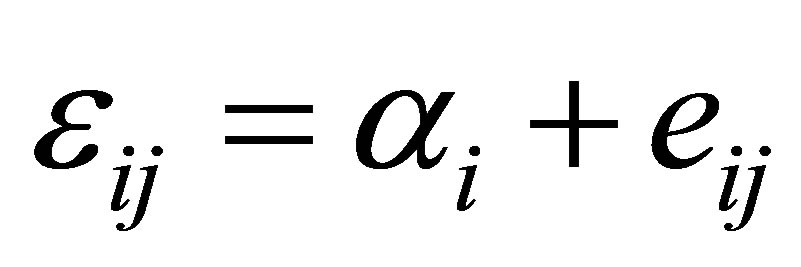 . Hence, an estimator for the variance component
. Hence, an estimator for the variance component  is derived as
is derived as
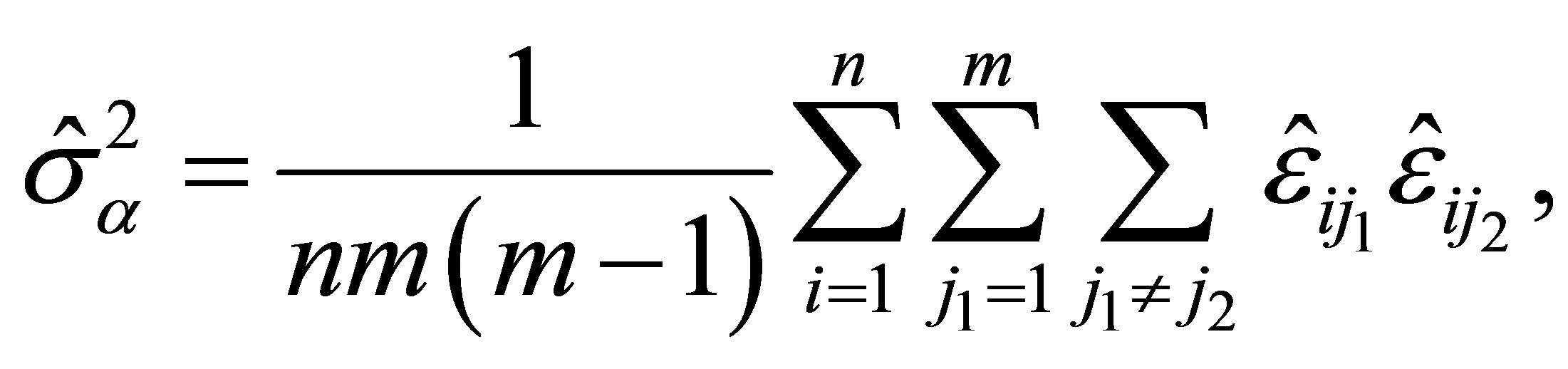
and
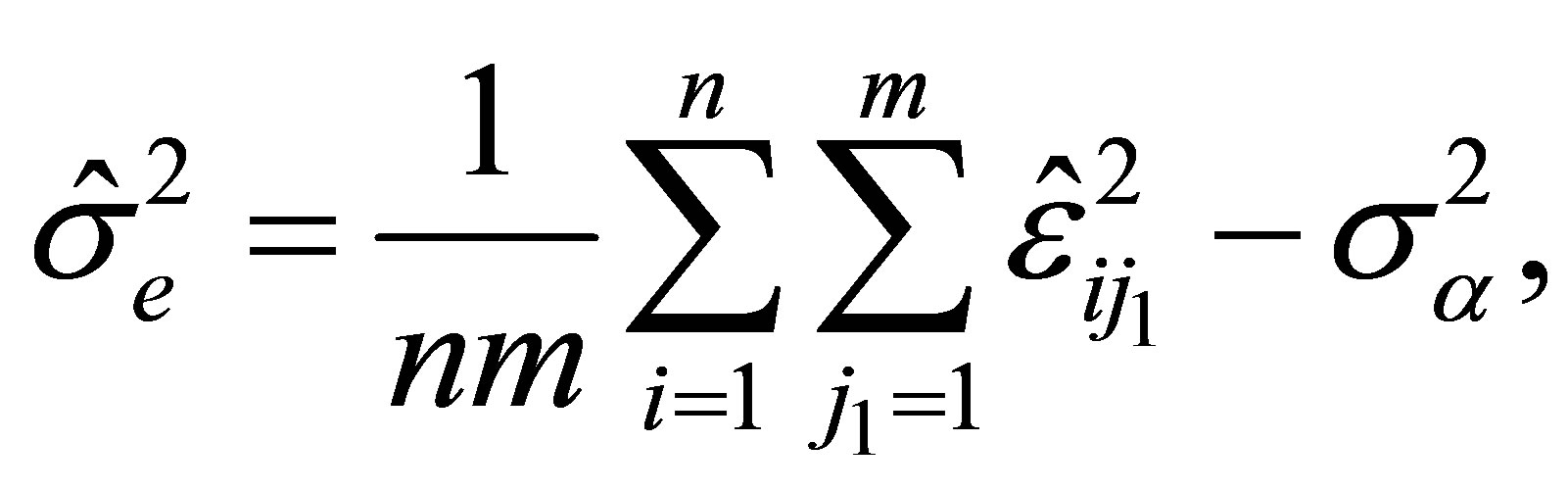 (10)
(10)
where with the preliminary estimator  for
for , the residual
, the residual  is defined as
is defined as
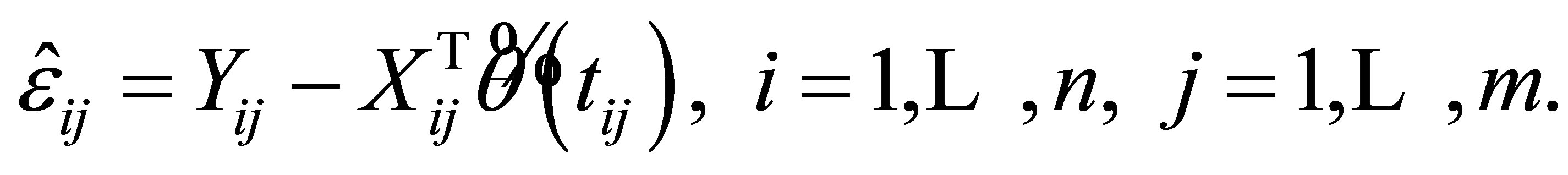
Therefore, we obtain the estimator for , that is
, that is
 (11)
(11)
Furthermore, with the true covariance in (4) being interpolated by the estimator (11), we derive a new auxiliary random vector
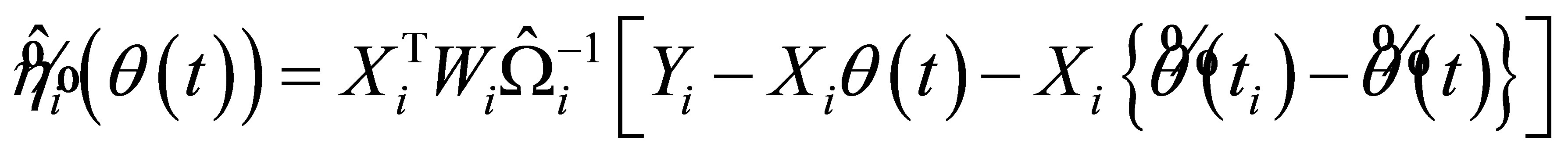 (12)
(12)
And, the newly estimated RABEL ratio function is
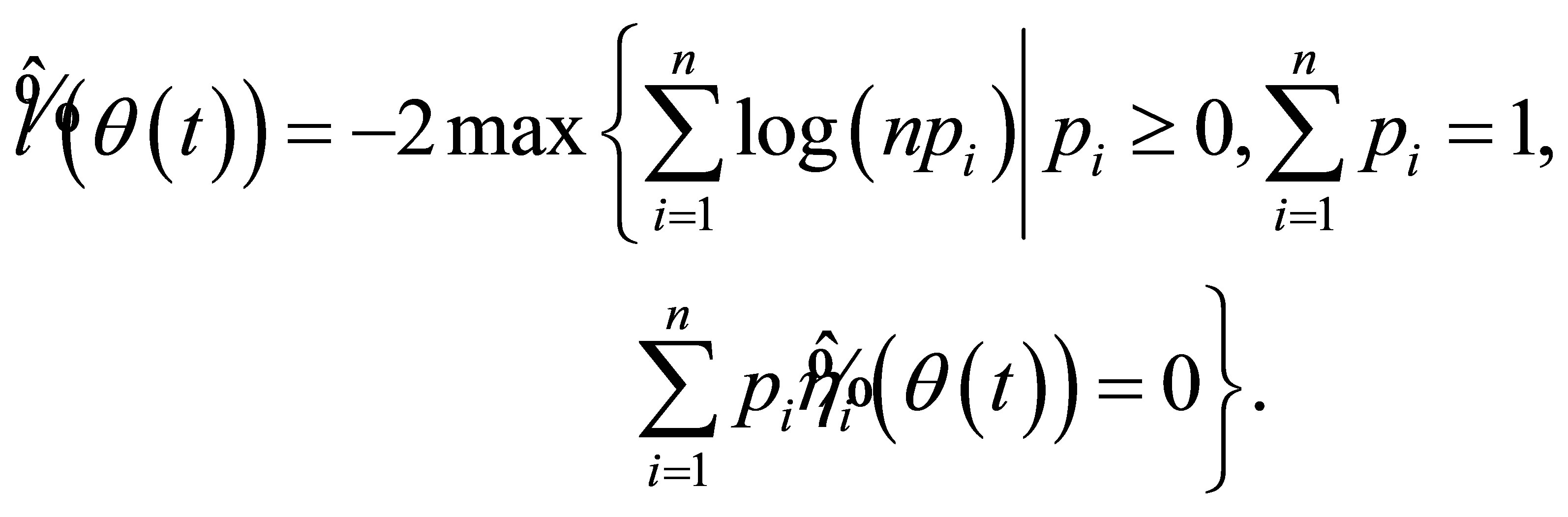 (13)
(13)
Additional implementation details of solving the preliminary estimator will be postponed to Section 4, after discussion of the asymptotic properties of the proposed method.
3. Asymptotic Result
In this section, we study the asymptotic properties of the estimators. Denote 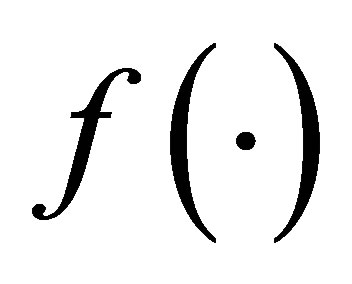 to be the density for covariate variable
to be the density for covariate variable .
.
Theorem 1. Suppose that conditions (C1)-(C6) in the Appendix hold, then
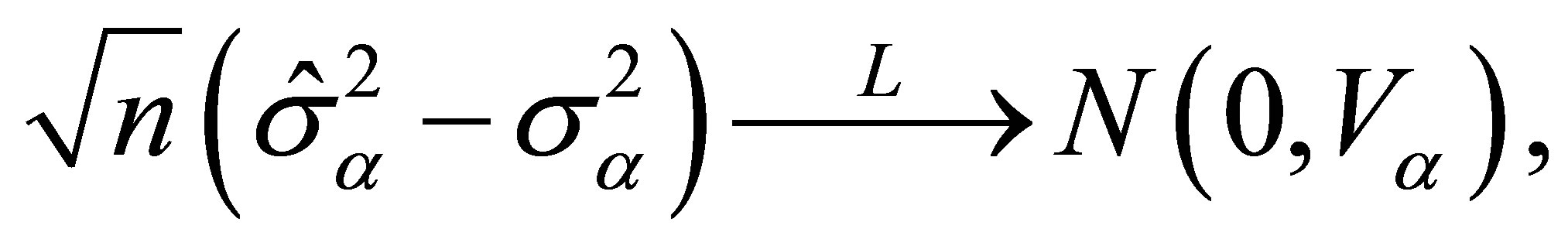 (14)
(14)
and
 (15)
(15)
where 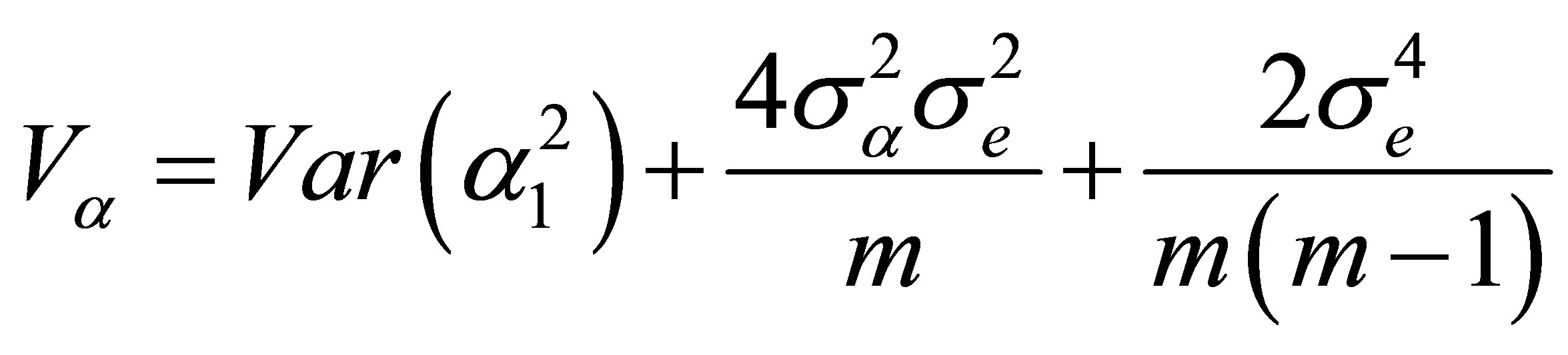 and
and 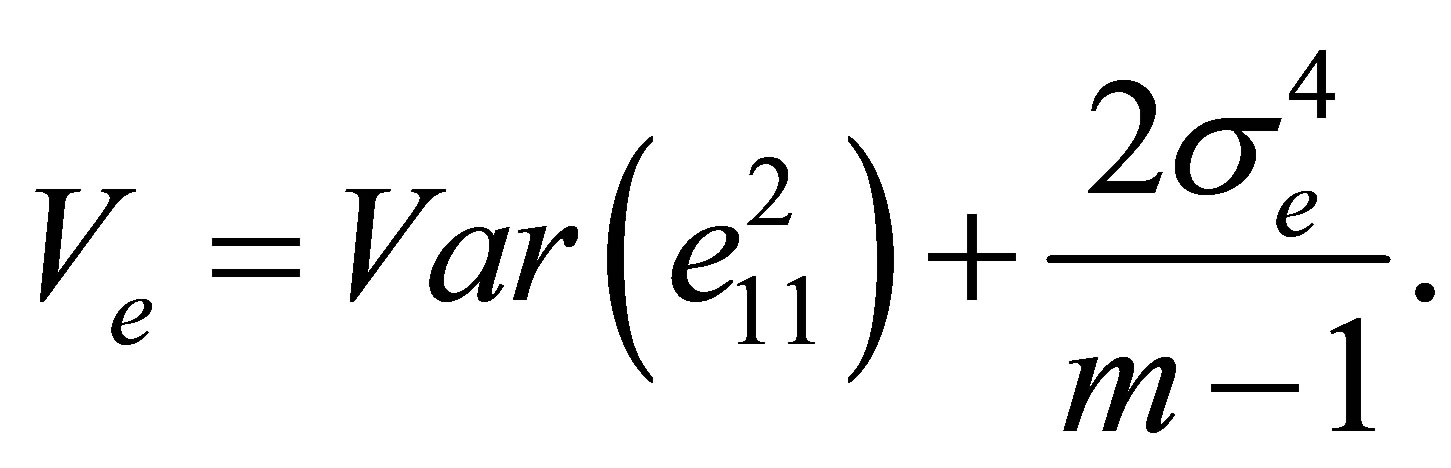
Theorem 2. Suppose that conditions (C1)-(C7) in the Appendix hold. If 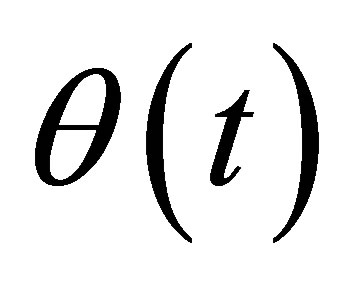 is the true value of the parameter, then
is the true value of the parameter, then
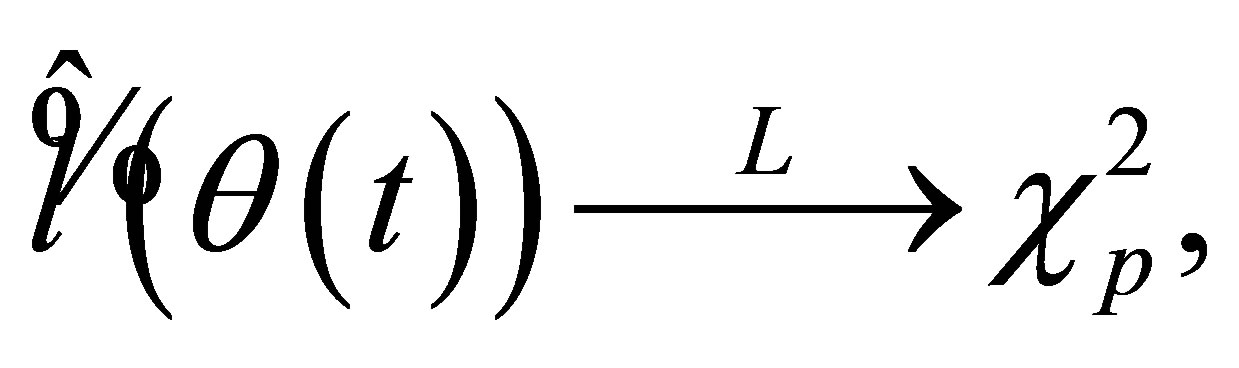 (16)
(16)
where 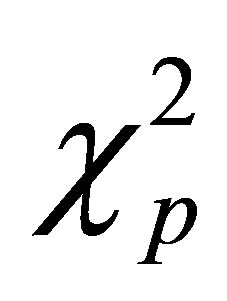 means a
means a  distribution with freedom
distribution with freedom .
.
Note that 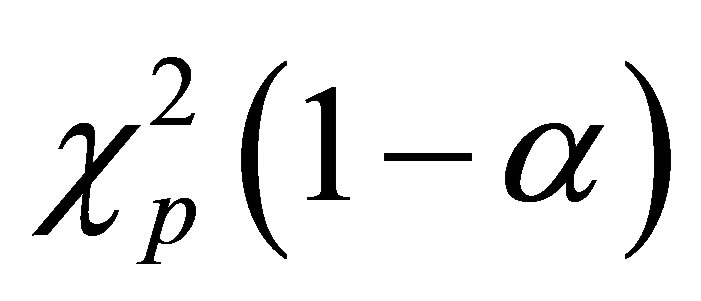 is the
is the 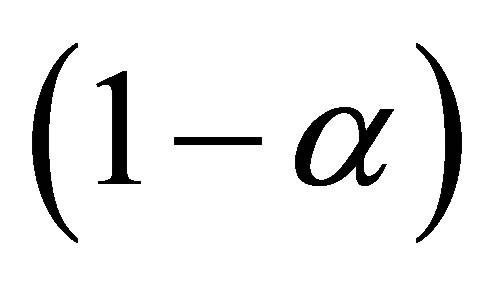 quantile of
quantile of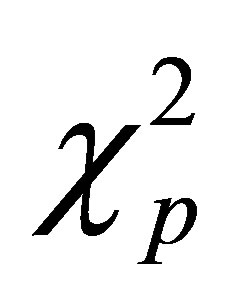 . Based on Theorem 2, we can derive the
. Based on Theorem 2, we can derive the  confidence interval of
confidence interval of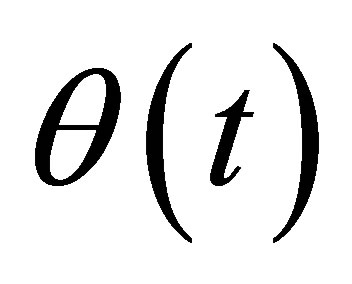 , that is
, that is
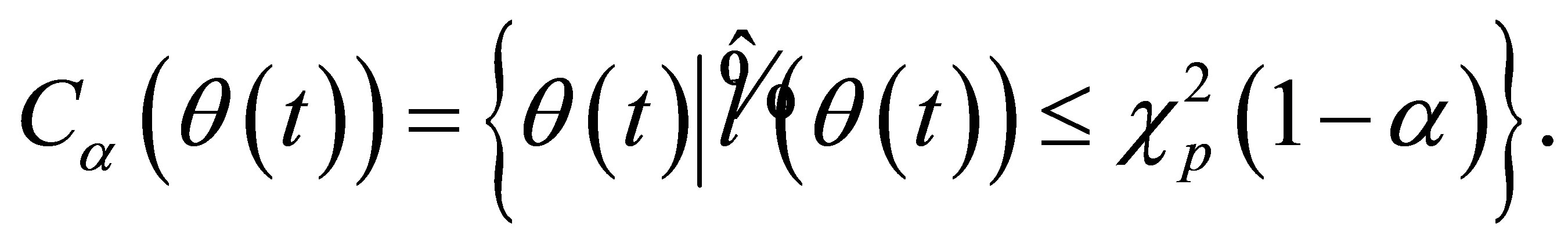
4. Implementation Issue
4.1. Calculation of the Preliminary Estimator
For t in the small neighborhood of , a Taylor expansion for the kth component of the varying coefficient function
, a Taylor expansion for the kth component of the varying coefficient function 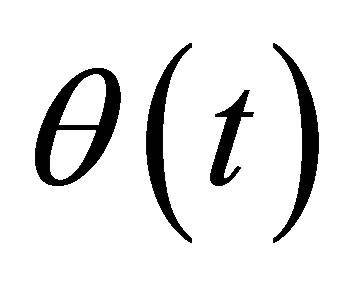 leads to
leads to
 (17)
(17)
where 
By ignoring the within-subject correlation, we can obtain the unknown vector a, b by minimizing
 (18)
(18)
where ,
,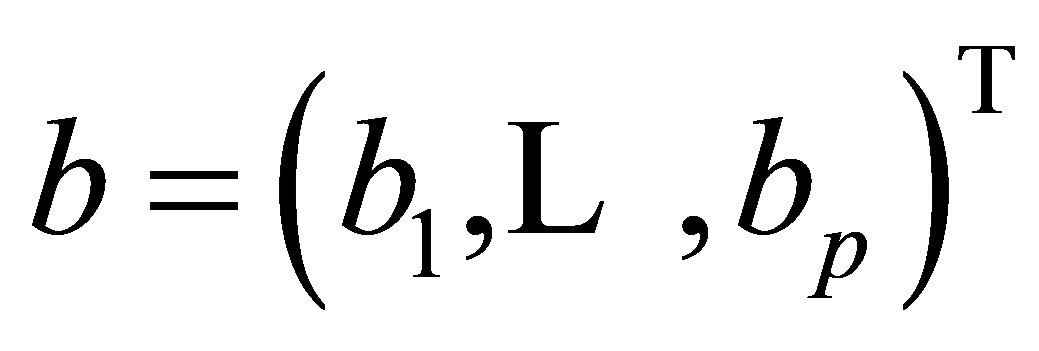 . Then, the solution to the minimization of (18) is
. Then, the solution to the minimization of (18) is

and

Specially, by the idea of local linear estimation, the preliminary estimator 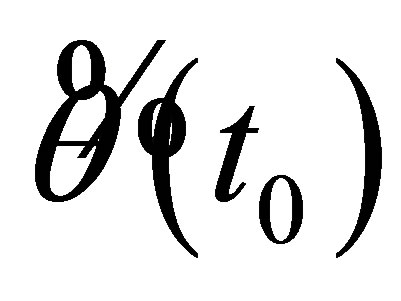 is followed by
is followed by
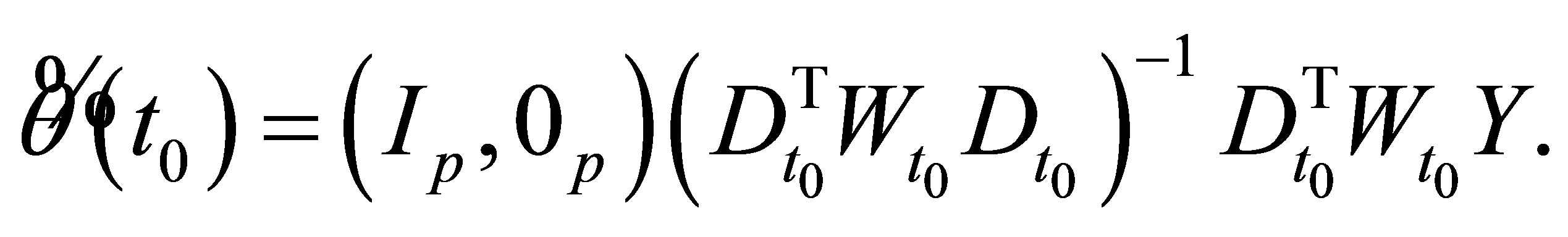 (19)
(19)
4.2. Choice of Bandwidth
As is well-known, the choice of bandwidth h can affect both the bias and variance estimation and there is a tradeoff between a proper bias and variance. A smaller variance arise with the choice of a large bandwidth value, whereas will increase the estimation bias. As pointed out by [3,13], an optimal bandwidth, which is selected by using the leave-one-subject-out cross validation, can satisfy the conditions. Therefore, in the following simulations in this article, we use kernel function 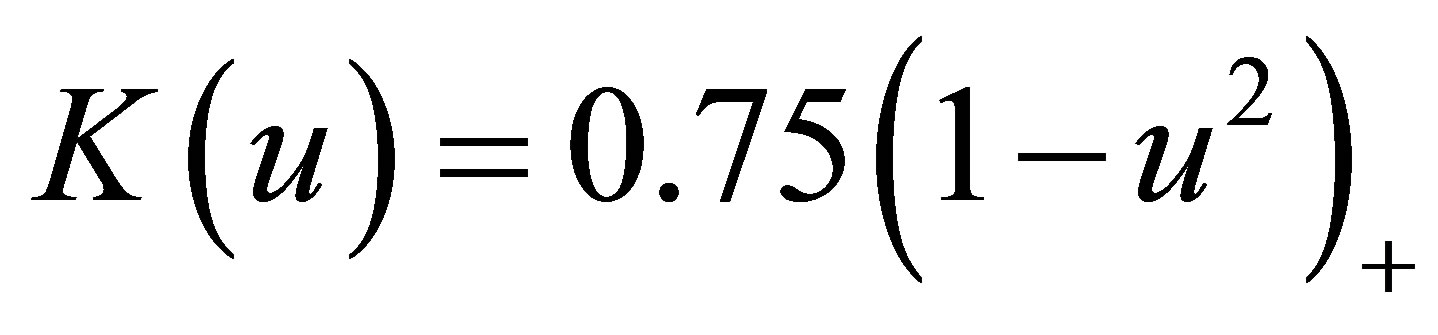 and the optimal bandwidth is obtained by minimizing
and the optimal bandwidth is obtained by minimizing
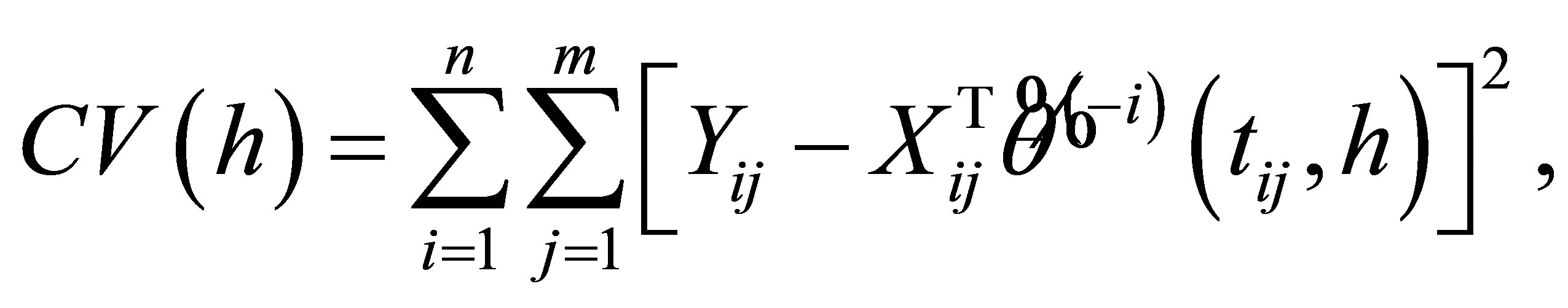
where 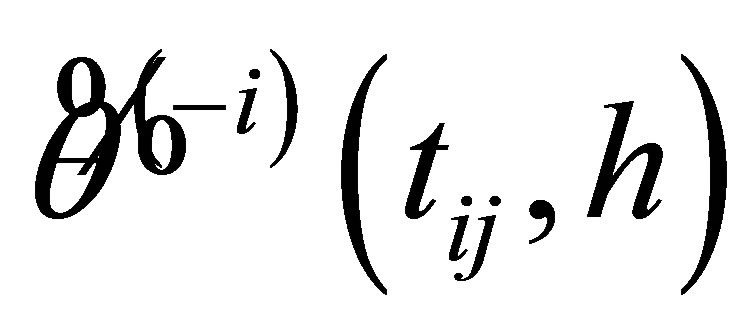 is denoted to be the preliminary estimator (19) estimated with all over the measurements except the ith subject.
is denoted to be the preliminary estimator (19) estimated with all over the measurements except the ith subject.
5. Empirical Study
In this section, we perform some Monte Carlo simulations to assess the finite sample performance of the proposed method. Assume the data is generated from the model
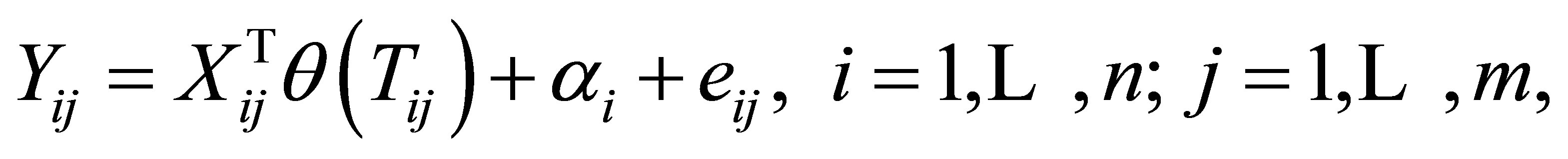 (20)
(20)
where 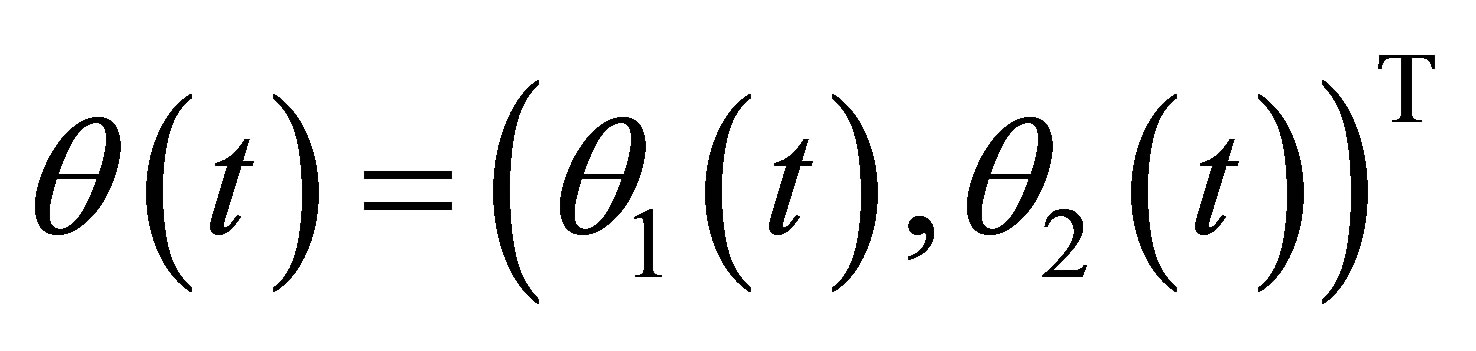 with
with 
and 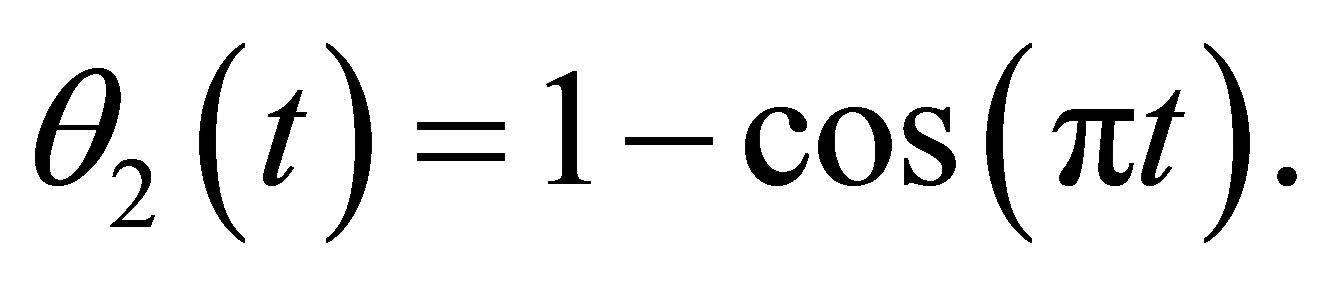 Moreover, we also assume that
Moreover, we also assume that
 and
and 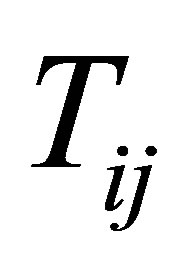 are generated from an uniform distribution on interval [0,1]. Meanwhile, denote that
are generated from an uniform distribution on interval [0,1]. Meanwhile, denote that 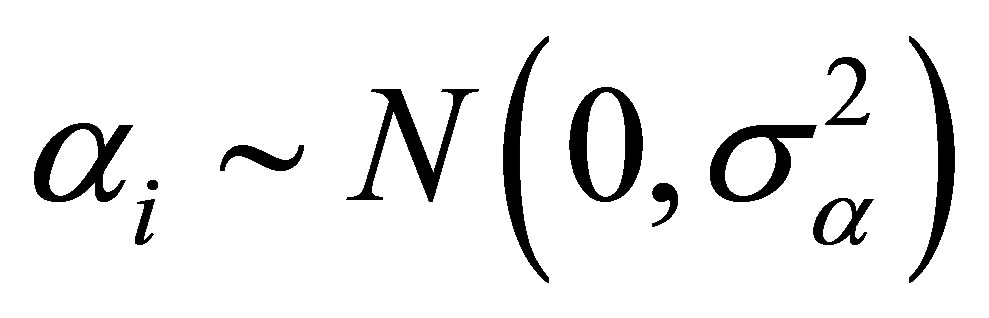 and
and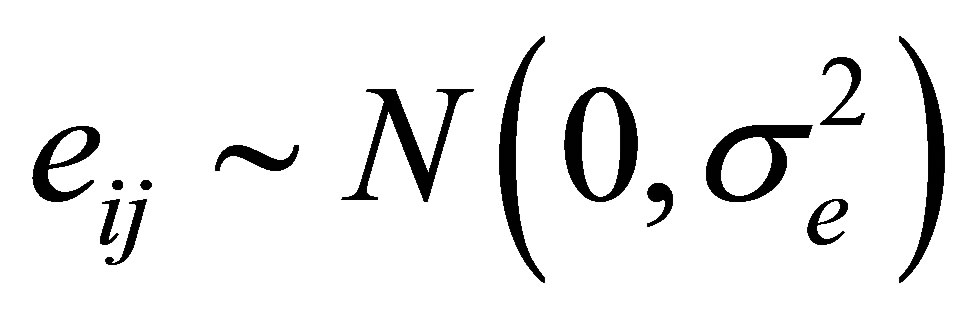 , where
, where 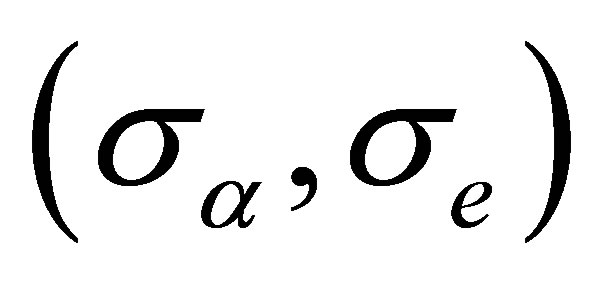 is set to be
is set to be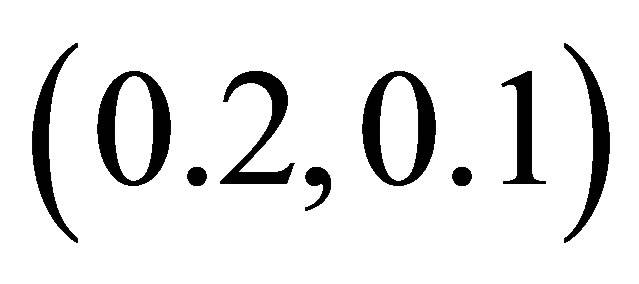 . It is assumed that the number of observed subject and repeated measurement within subject are n = 100 and m = 3. For the purpose of intensive comparison, in addition to the proposed procedure during the simulations, a “naive” approach, based on the working independence assumption, is also involved, assuming that the within cluster covariance matrices are identities. The simulation results were calculated by 100 runs.
. It is assumed that the number of observed subject and repeated measurement within subject are n = 100 and m = 3. For the purpose of intensive comparison, in addition to the proposed procedure during the simulations, a “naive” approach, based on the working independence assumption, is also involved, assuming that the within cluster covariance matrices are identities. The simulation results were calculated by 100 runs.
Figure 1 reports the approximate 95% point-wise confidence intervals and their coverage probability curves for the coefficient function 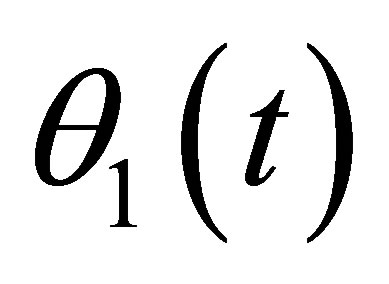 and
and , calculated by the proposed method in this article and the “naive” method. Although from Figure 1, two methods construct close confidence intervals for the nonparametric component, the coverage probability curves in the right panels show a significant difference. The coverage probability curves, estimated with the proposed method in this article, are closer to the significance lever 95% and possess a more stable and superior performance.
, calculated by the proposed method in this article and the “naive” method. Although from Figure 1, two methods construct close confidence intervals for the nonparametric component, the coverage probability curves in the right panels show a significant difference. The coverage probability curves, estimated with the proposed method in this article, are closer to the significance lever 95% and possess a more stable and superior performance.
By the two required methods, we construct the simultaneous confidence regions of 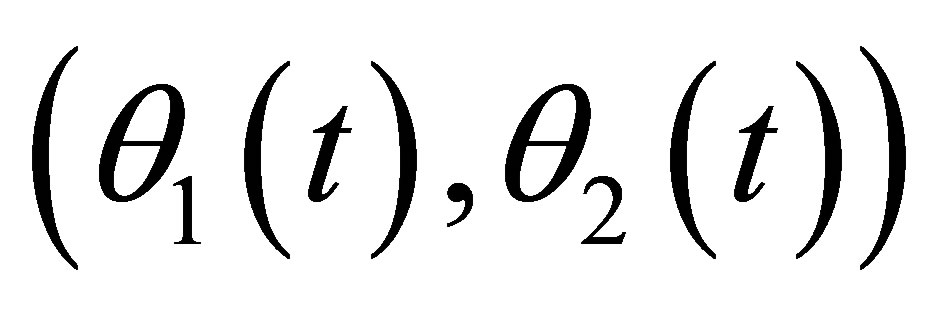 at time point
at time point 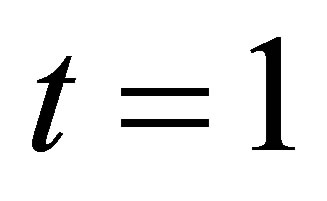 in Figure 2. The two plot are designed with
in Figure 2. The two plot are designed with 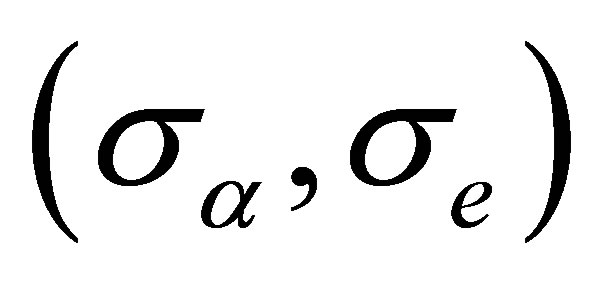 being (0.1,0.1) and (0.2,0.1), respectively. Direct comparison of them illustrates the inference improvement of the proposed RABEL method on that “naive” one.
being (0.1,0.1) and (0.2,0.1), respectively. Direct comparison of them illustrates the inference improvement of the proposed RABEL method on that “naive” one.
6. Real Application
To illustrate the effectiveness of the proposed inference procedure in this article, we apply it to the analysis of a longitudinal AIDS data set, reported by [5]. Some inference methods are related in literatures of [3,4,17]. However, there is limited work of them that focused on the within-subject correlation under the random effect framework. In fact, when we use the Hausman test for the null hypothesis of the random effect, the random effect is approved at 5% level of significance with p-value 85.9%, which can be calculated by the R function phtest() in the plm package.
As to the jth measurement of the ith subject, let 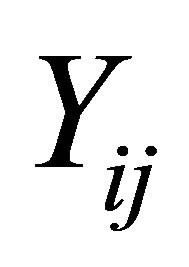 be CD4 percentage,
be CD4 percentage,  be the time in years after HIV infection,
be the time in years after HIV infection, 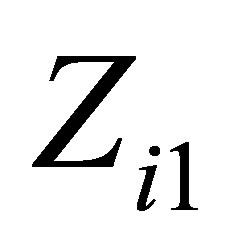 be the centered age at HIV infection,
be the centered age at HIV infection, 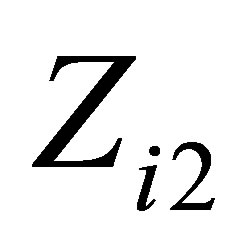 be the centered preCD4 percentage, and
be the centered preCD4 percentage, and 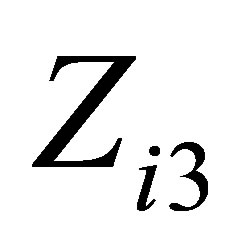 be the smoking status, taking a value of 1 or 0 for smoker or nonsmoker. Hence, we consider the following varying coefficient model with random effect
be the smoking status, taking a value of 1 or 0 for smoker or nonsmoker. Hence, we consider the following varying coefficient model with random effect
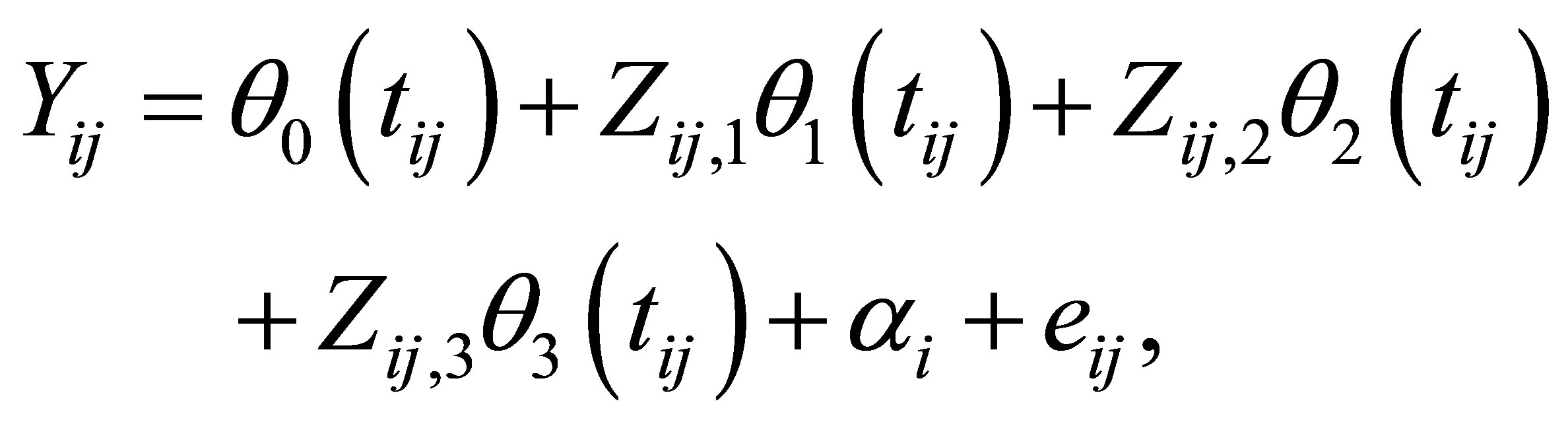 (21)
(21)
where the baseline CD4 percentage curve  is used to represent the mean CD4 percentage of t years after the infection. By the proposed inference procedure in this article, we plot the curves of the unknown coefficient functions in model (21) and their approximate 95% confidence intervals in Figure 3. From the curve of baseline
is used to represent the mean CD4 percentage of t years after the infection. By the proposed inference procedure in this article, we plot the curves of the unknown coefficient functions in model (21) and their approximate 95% confidence intervals in Figure 3. From the curve of baseline
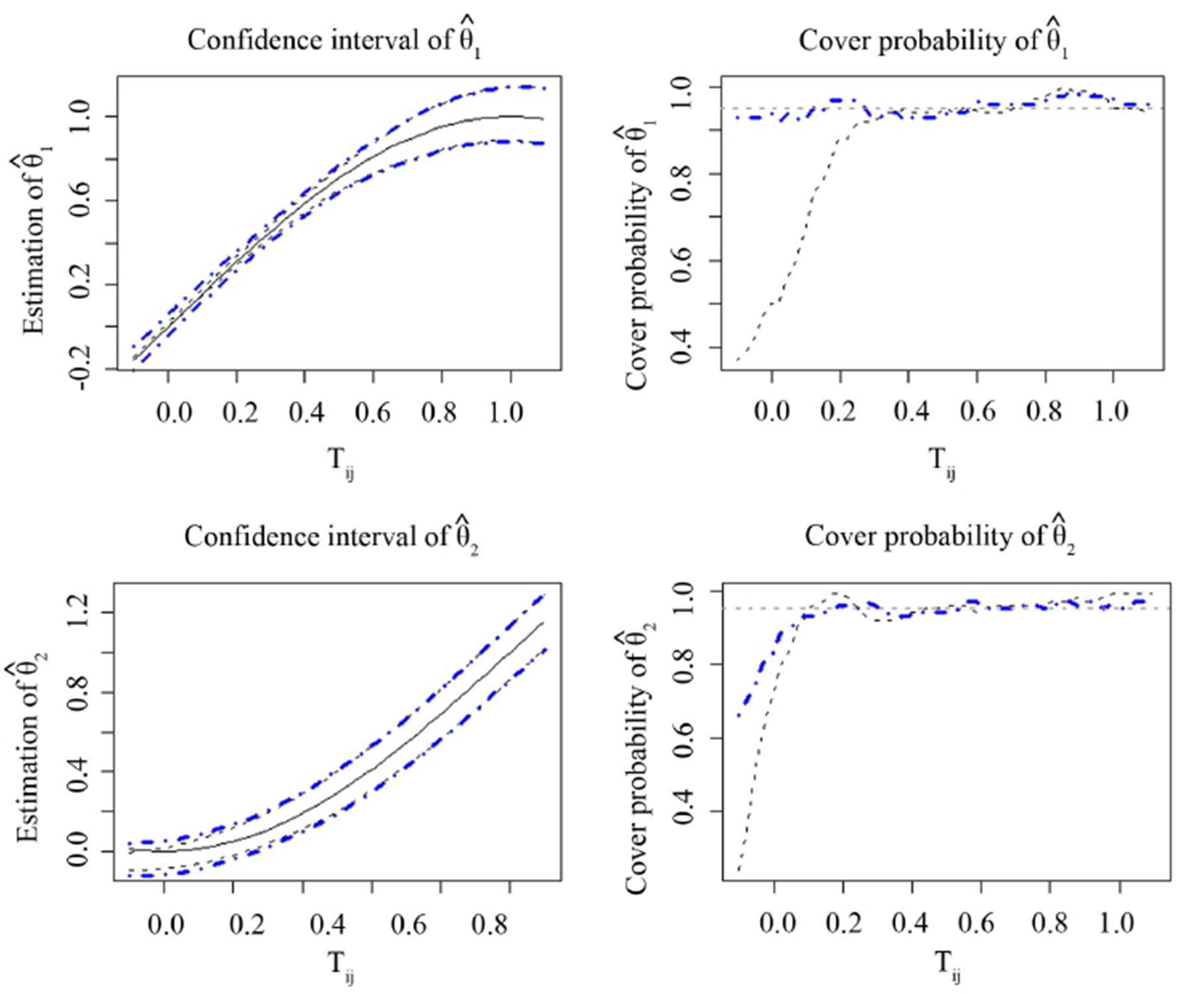
Figure 1. The true curve and its 95% confidence interval of the varying coefficient function are shown in the left two panels. On the other hand, the right two panels show the coverage probability curve of the corresponding confidence interval. And all the dashed and dotted-dashed curve are estimated by ignoring and considering the within-subject correlation, respectively.
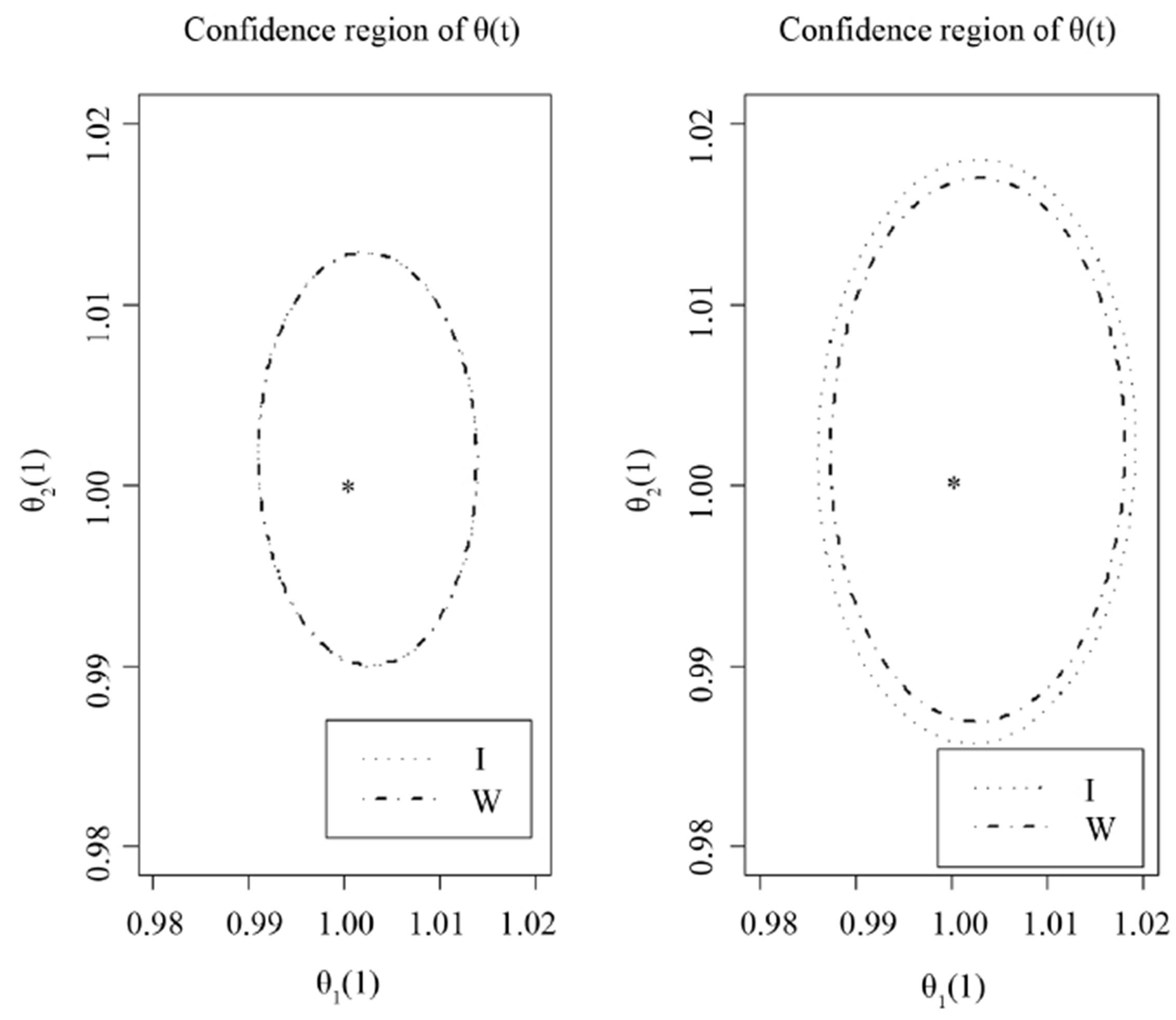
Figure 2. The simultaneous confidence region of the two varying coefficient functions at point t = 1, with dashed and dotteddashed curve being estimated by ignoring and considering the within-subject correlation, respectively. The left and right panel are for 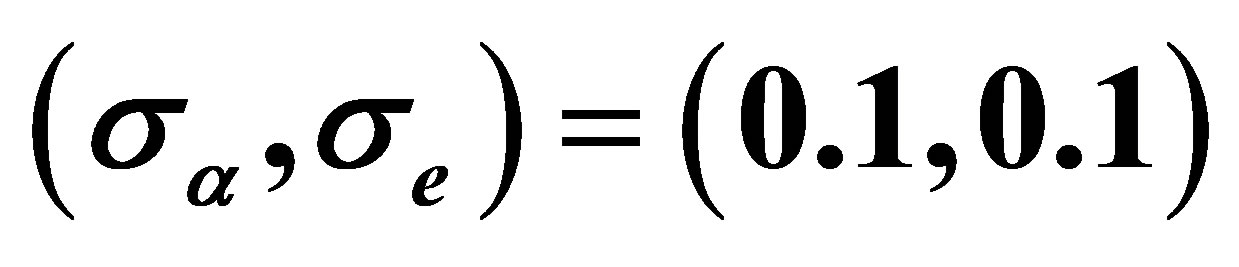 and
and , respectively.
, respectively.
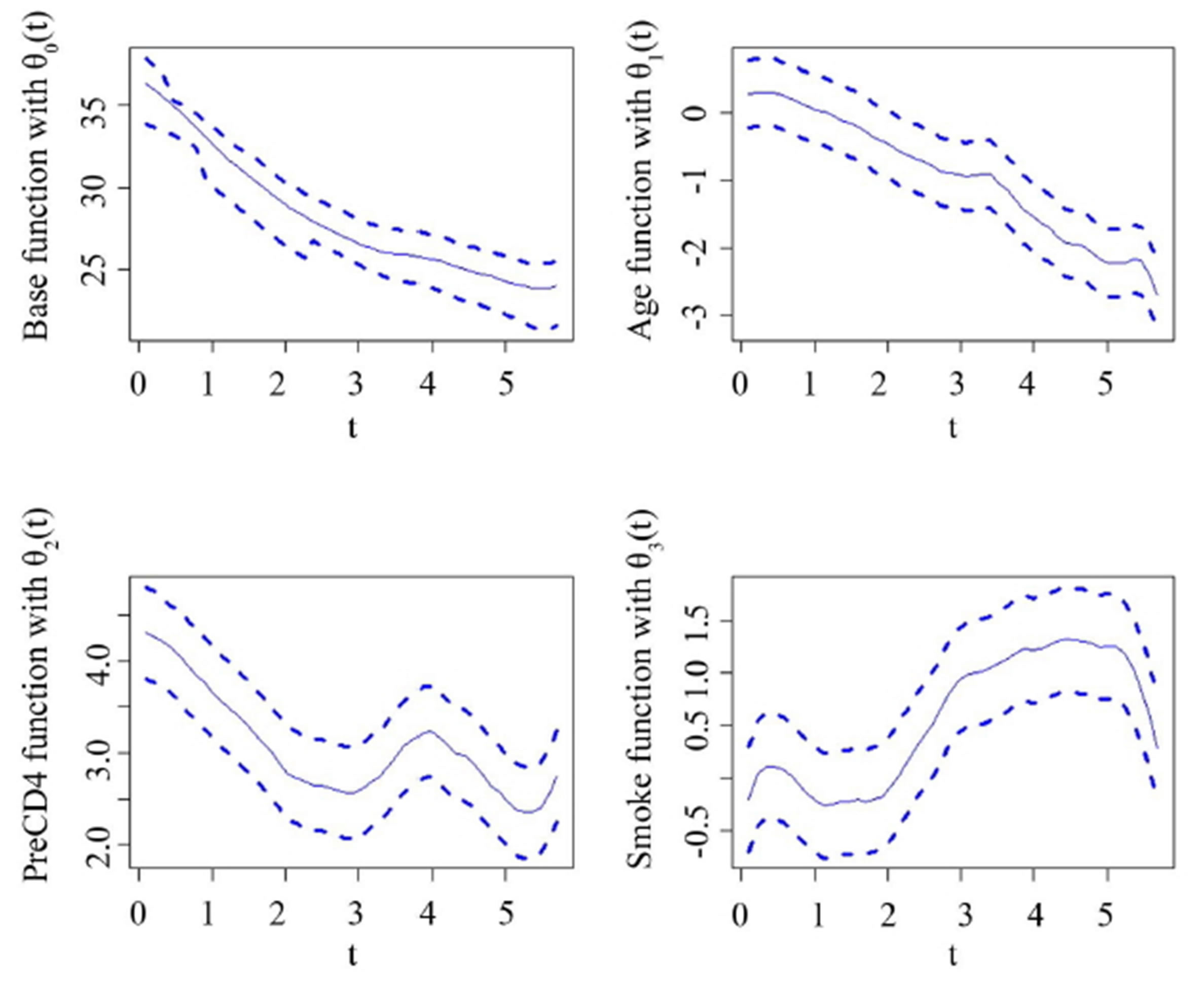
Figure 3. The four plots show the changing curve and their corresponding 95% confidence interval for the different covariate variables as baseline curve, Age, PreCD4, and Smoke status.
function in Figure 3, we can find that the estimated curve of the mean CD4 percentage depletion over time also indicate that after getting infected, the CD4 counts decreases sharply at the first 4 years and then the decreasing rate becomes slower although it sometimes changes a little, which is similar to the arguments in [3, 17,18]. Moreover, other estimated curves in Figure 3 suggest the dependence of CD4 percentage on other variable, such as age, preCD4 and smoke status. Specially, the curve about the variable preCD4 is similar to that shown in Figure 4 in [4], although small nonlinear changing tendency was found in [3].
7. Acknowledgements
This work was partially supported by National Natural Science Foundation of China (11171012, Key program: 11331011), Science and Technology Project for the Supervisor of Excellent Doctoral Dissertation of Beijing (20111000503), Specialized Research Fund for the Doctoral Program of Higher Education of China (20121103110004) and the Beijing Municipal Key Disciplines (No.006000541212010).
REFERENCES
- C. T. Chiang, J. A. Rice and C. O. Wu, “Smoothing Spline Estimation for Varying Coefficient Models with Repeatedly Measured Dependent Variables,” Journal of the American Statistical Association, Vol. 96, No. 454, 2001, pp. 605-619.
- A. Qu and R. Li, “Quadratic Inference Functions for Varying Coefficient Models with Longitudinal Data,” Biometrics, Vol. 62, No. 2, 2006, pp. 379-391. http://dx.doi.org/10.1111/j.1541-0420.2005.00490.x
- L. G. Xue and L. X. Zhu, “Empirical Likelihood for a Varying Coefficient Model with Longitudinal Data,” Journal of the American Statistical Association, Vol. 102, No. 478, 2007, pp. 642-652. http://dx.doi.org/10.1198/016214507000000293
- H. J. Wang, Z. Zhu and J. Zhou, “Quantile Regression in Partially Linear Varying Coefficient Models,” Annals of Statistics, Vol. 37, No. 6B, 2009, pp. 3841-3866.
- R. A. Kaslow, D. G. Ostrow, R. Detels, J. P. Phair, B. F. Polk and C. R. Rinaldo, “The Multicenter AIDS Cohort Study: Rationale, Organization and Selected Characteristics of the Participants,” American Journal of Epidemiology, Vol. 126, No. 2, 1987, pp. 310-318. http://dx.doi.org/10.1093/aje/126.2.310
- Q. Li and A. Ullah, “Estimating Partially Linear Panel Data Models with One-way Error Components,” Econometric Reviews, Vol. 17, No. 2, 1998, pp. 145-166. http://dx.doi.org/10.1080/07474939808800409
- C. Gu and P. Ma, “Optimal Smoothing in Nonparametric Mixed Effect Models,” Annals of Statistics, Vol. 33, No. 3, 2005, pp. 1357-1379. http://dx.doi.org/10.1214/009053605000000110
- J. You, X. Zhou and Y. Zhou, “Statistical Inference for Panel Data Semiparametric Partially Linear Regression Models with Heteroscedastic Errors,” Journal of Multivariate Analysis, Vol. 101, No. 5, 2010, pp. 1079-1101. http://dx.doi.org/10.1016/j.jmva.2010.01.003
- Z. Pang and L. G. Xue, “Estimation for the Single-index Models with Random Effects,” Computational Statistics & Data Analysis, Vol. 56, No. 6, 2012, pp. 1837-1853. http://dx.doi.org/10.1016/j.csda.2011.11.007
- A. B. Owen, “Empirical Likelihood Ratio Confidence Intervals for a Single Functional,” Biometrika, Vol. 75, No. 2, 1988, pp. 237-249. http://dx.doi.org/10.1093/biomet/75.2.237
- A. Owen, “Empirical Likelihood Ratio Confidence Regions,” Annals of Statistics, Vol. 18, No. 1, 1990, pp. 90- 120. http://dx.doi.org/10.1214/aos/1176347494
- A. Owen, “Empirical Likelihood for Linear Models,” Annals of Statistics, Vol. 19, No. 4, 1991, pp. 1725-1747. http://dx.doi.org/10.1214/aos/1176348368
- P. Zhao and L. Xue, “Empirical Likelihood Inferences for Semiparametric Varying Coefficient Partially Linear Errors in Variables Models with Longitudinal Data,” Journal of Nonparametric Statistics, Vol. 21, No. 7, 2009, pp. 907-923. http://dx.doi.org/10.1080/10485250902980576
- G. R. Li, P. Tian and L. G. Xue, “Generalized Empirical Likelihood Inference in Semiparametric Regression Model for Longitudinal Data,” Acta Mathematica Sinica, Vol. 24, No. 12, 2008, pp. 2029-2040. http://dx.doi.org/10.1007/s10114-008-6434-7
- K. Y. Liang and S. L. Zeger, “Longitudinal Data Analysis Using Generalised Linear Models,” Biometrika, Vol. 73, No. 1, 1986, pp. 12-22. http://dx.doi.org/10.1093/biomet/73.1.13
- J. You, G. Chen and Y. Zhou, “Block Empirical Likelihood for Longitudinal Partially Linear Regression Models,” Canadian Journal of Statistics, Vol. 34, No. 1, 2006, pp. 79-96. http://dx.doi.org/10.1002/cjs.5550340107
- P. Zhao and L. Xue, “Variable Selection for Semiparametric Varying Coefficient Partially Linear Errors in Variables Models,” Journal of Multivariate Analysis, Vol. 101, No. 8, 2010, pp. 1872-1883. http://dx.doi.org/10.1016/j.jmva.2010.03.005
- J. Fan and R. Li, “New Estimation and Model Selection Procedures for Semiparametric Modeling in Longitudinal Data Analysis,” Journal of the American Statistical Association, Vol. 99, No. 467, 2004, pp. 710-723. http://dx.doi.org/10.1198/016214504000001060
- H. G. M¨uller and J. M. Chiou, “Nonparametric QuasiLikelihood,” Annals of Statistics, Vol. 27, No. 1, 1999, pp. 36-64. http://dx.doi.org/10.1214/aos/1018031100
- D. A. Harville, “Matrix Algebra from a Statistician’s Perspective,” Springer, New York, 1997. http://dx.doi.org/10.1007/b98818
- G. A. F. Seber, “A Matrix Handbook for Statisticians,” John Wiley & Sons, Hoboken, 2007. http://dx.doi.org/10.1002/9780470226797
- Y. Li, “Efficient Semiparametric Regression for Longitudinal Data with Nonparametric Covariance Estimation,” Biometrika, Vol. 98, No. 2, 2011, pp. 355-370. http://dx.doi.org/10.1093/biomet/asq080
Appendix
Condition 1. The bandwidth satisfies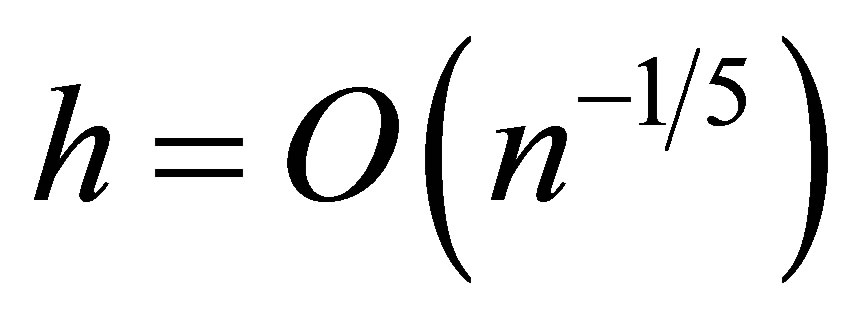 .
.
Condition 2. The kernel K(·), a symmetric probability density function, is twice continuously differentiable at
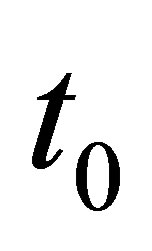 and satisfies
and satisfies .
.
Condition 3. The intensity 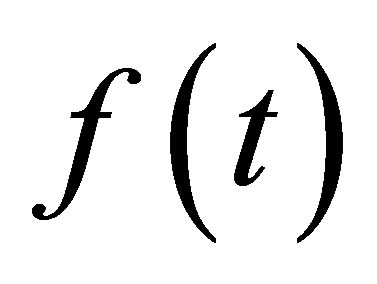 of covariate variable
of covariate variable 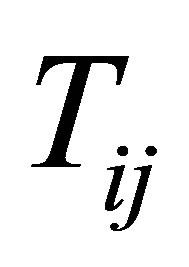 is bounded away from 0 and infinity on [0,1], and is continuously differentiable on (0,1).
is bounded away from 0 and infinity on [0,1], and is continuously differentiable on (0,1).
Condition 4.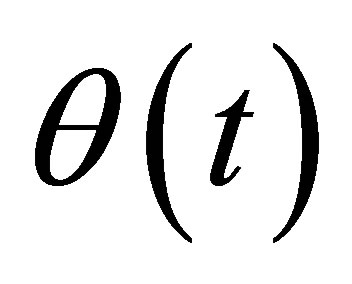 ,
,  are twice continuously differentiable on
are twice continuously differentiable on , where
, where
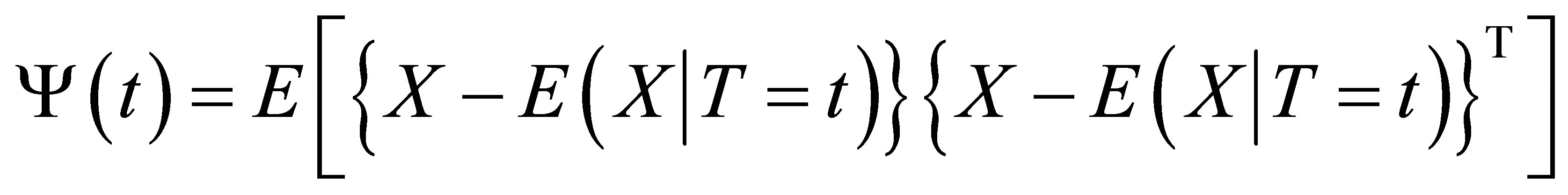
Condition 5. 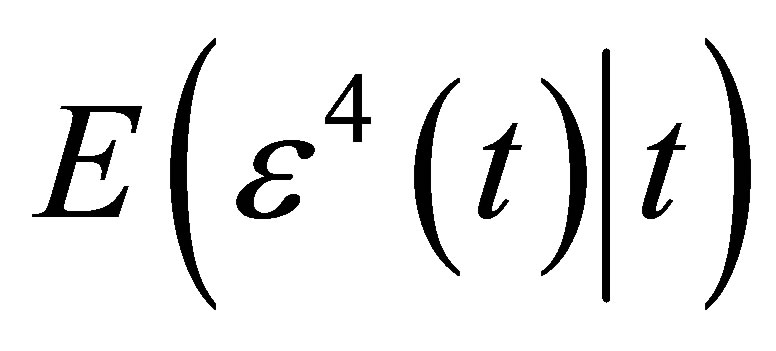 and
and 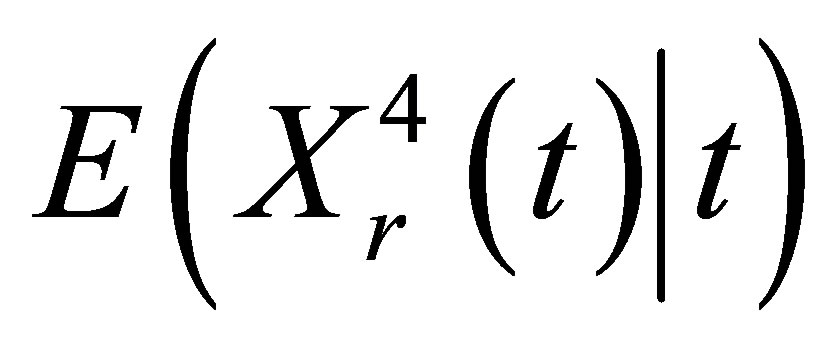 are twice continuous with t, and
are twice continuous with t, and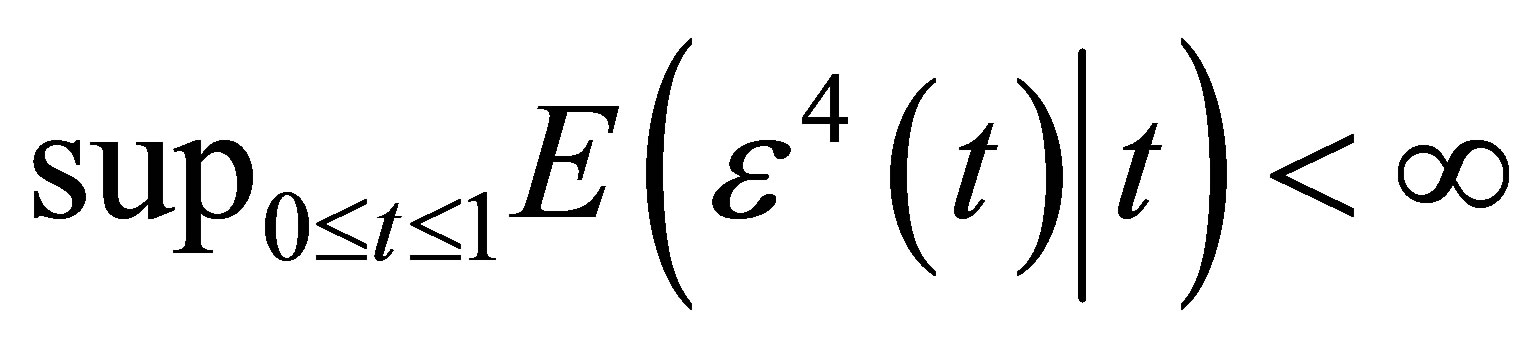 ,
, 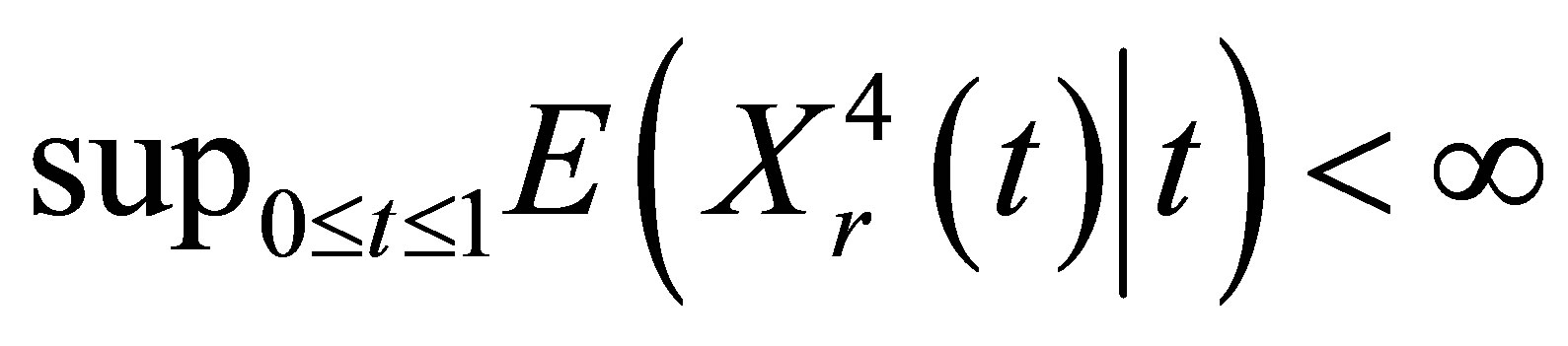 , where
, where 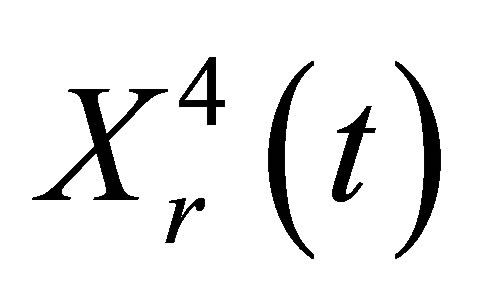 is rth component of
is rth component of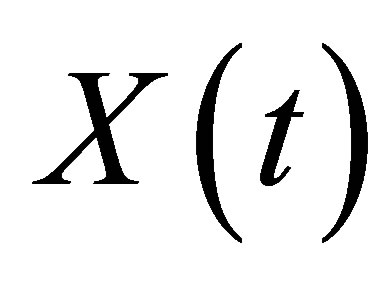 .
.
Condition 6. For given t,  is positive definite matrix.
is positive definite matrix.
Condition 7. There exist two positive constants 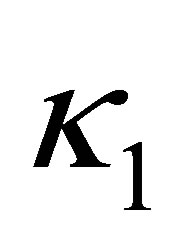 and
and , such that
, such that
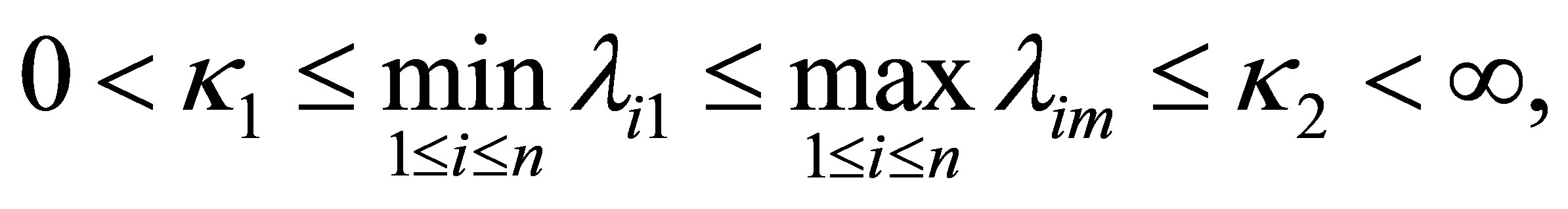
where 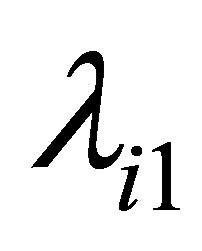 and
and  denote to be the smallest and largest eigenvalues of
denote to be the smallest and largest eigenvalues of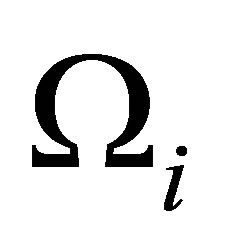 , respectively.
, respectively.
Lemma 1. Suppose that conditions (C1)-(C6) hold, 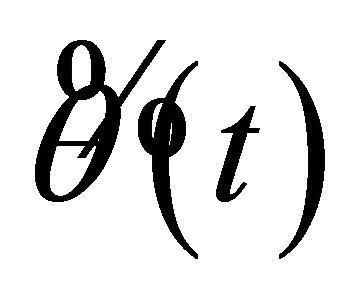 denote to be the preliminary estimators solved by the estimation Equation (19), then we have
denote to be the preliminary estimators solved by the estimation Equation (19), then we have
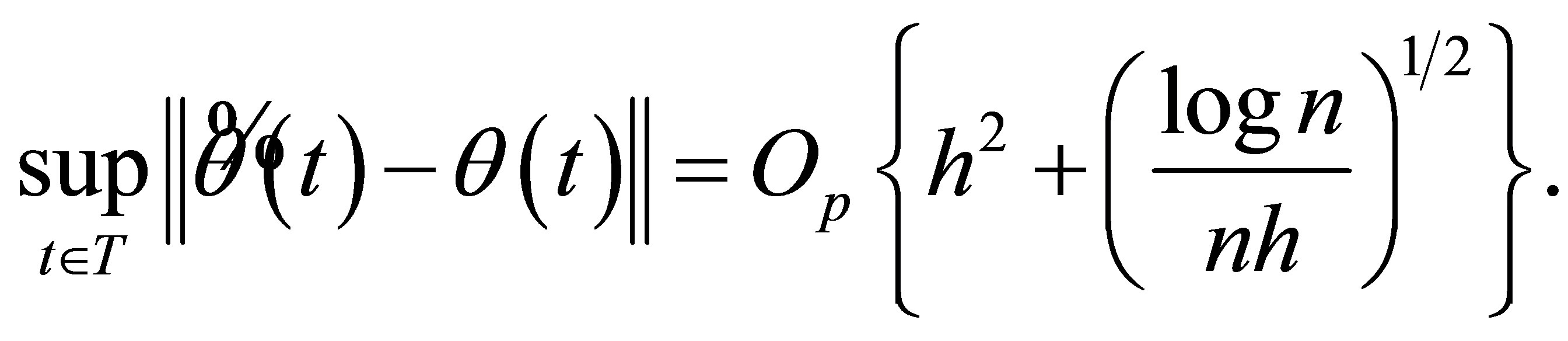 (A.1)
(A.1)
Proof. See the proof of Lemma 4.1 in [19].
Lemma 2. Let 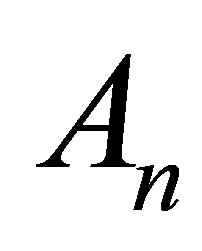 be a sequence of random matrices converging to an invertible matrix A. Then
be a sequence of random matrices converging to an invertible matrix A. Then
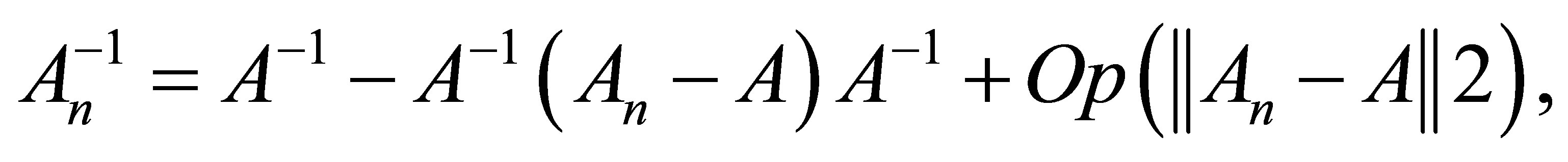 (A.2)
(A.2)
where 
Proof. See the proof in [20-22].
Lemma 4. Assume the conditions (C1)-(C7) hold, and 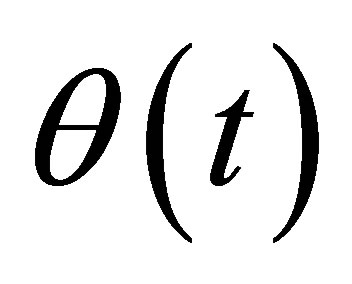 is the true parameter, then
is the true parameter, then
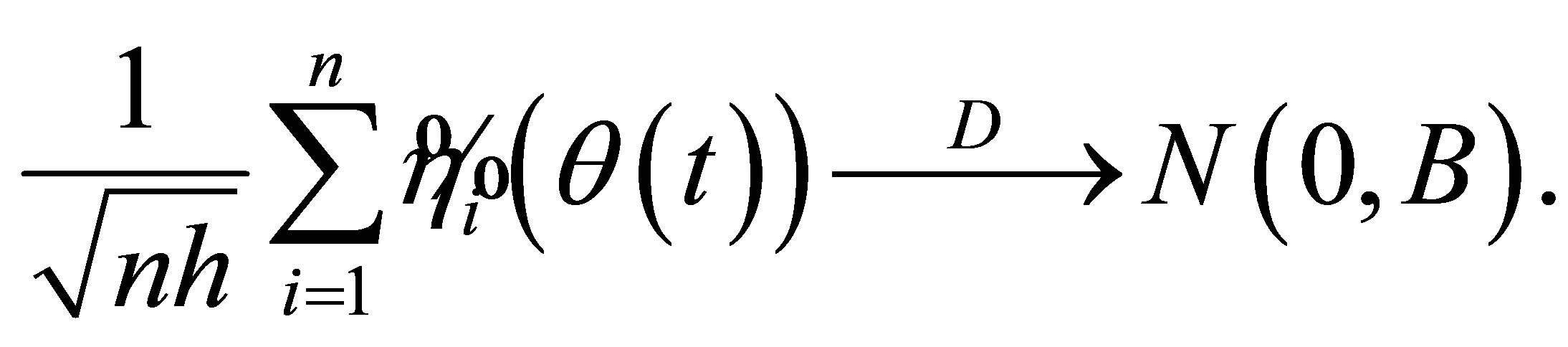
Proof. 
where
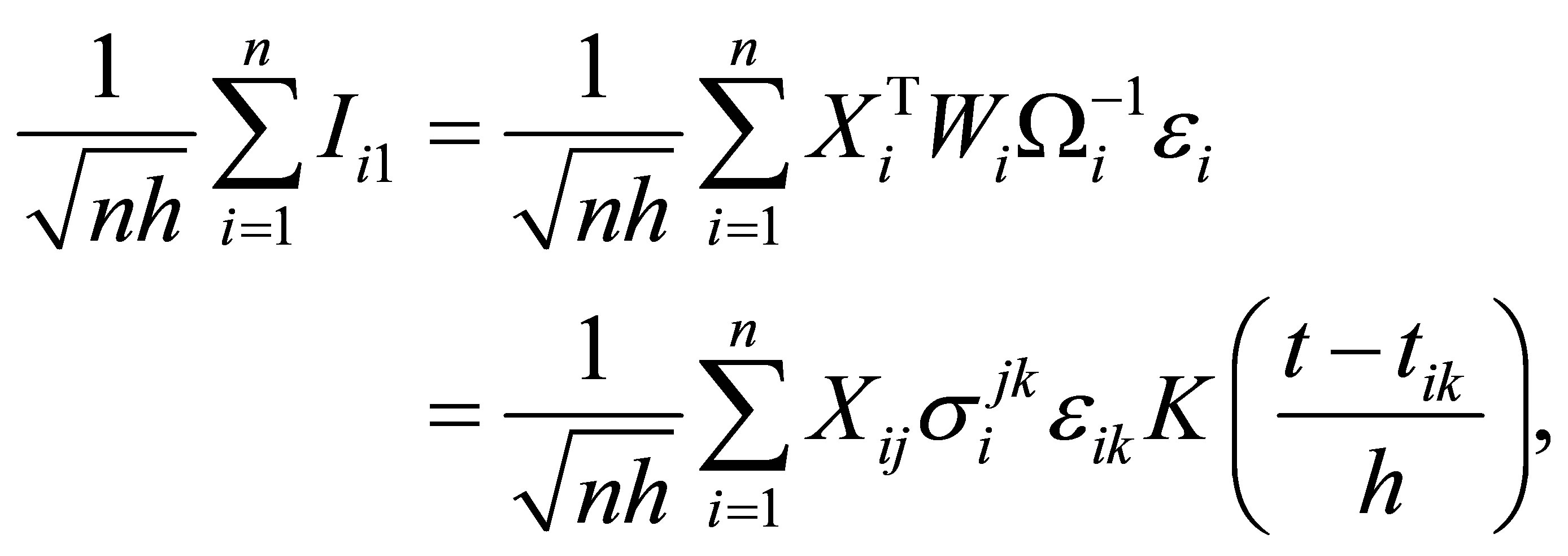


With several calculation and the Central Limit Theorem,
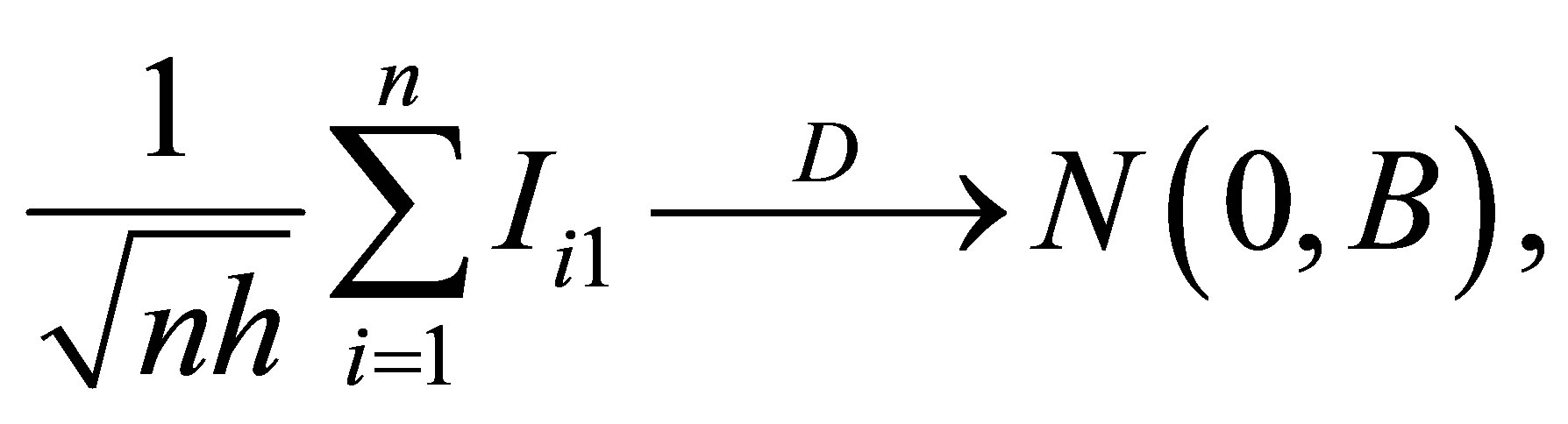 (A.3)
(A.3)
and 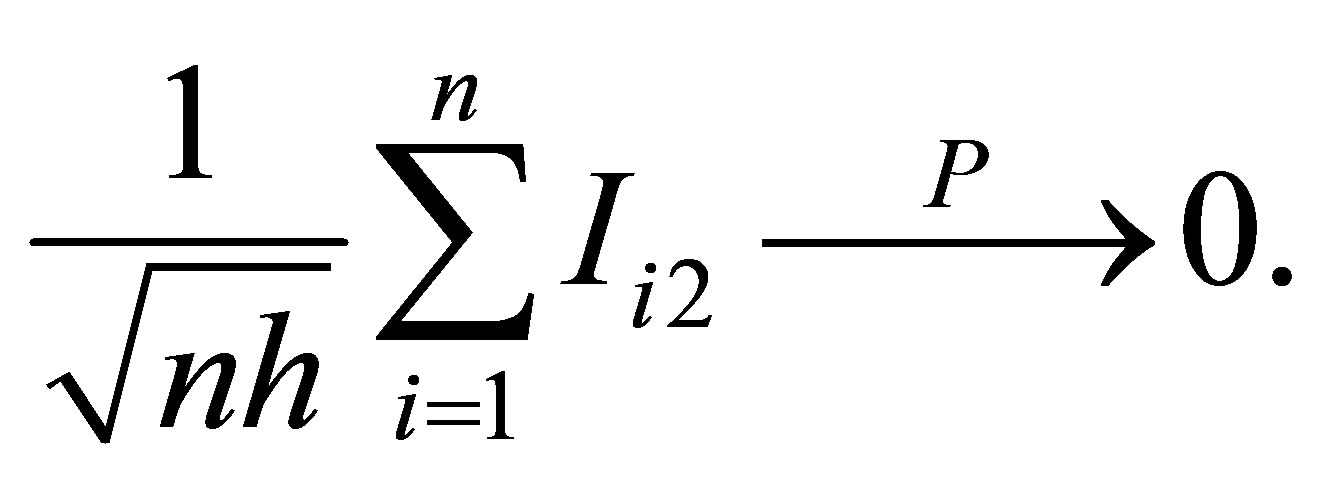
Therefore, Lemma 4 can be derived directly.
Lemma 5. Assume the conditions (C1)-(C7) hold, and 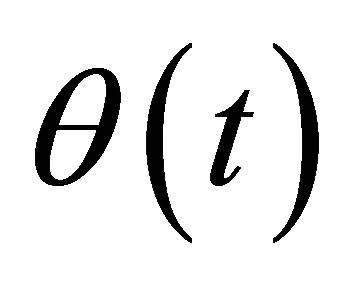 is the true parameter, then
is the true parameter, then
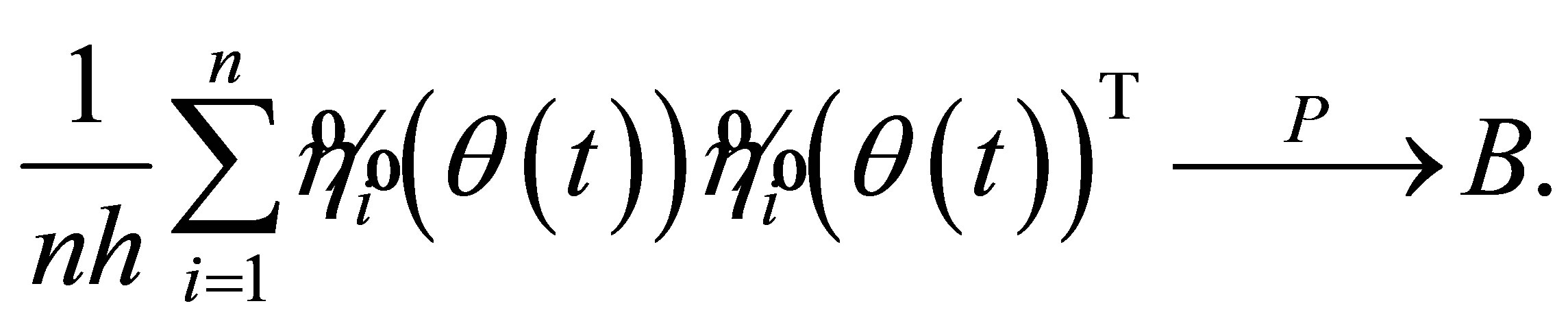
Proof. By the proof of Lemma 4, we can derive that
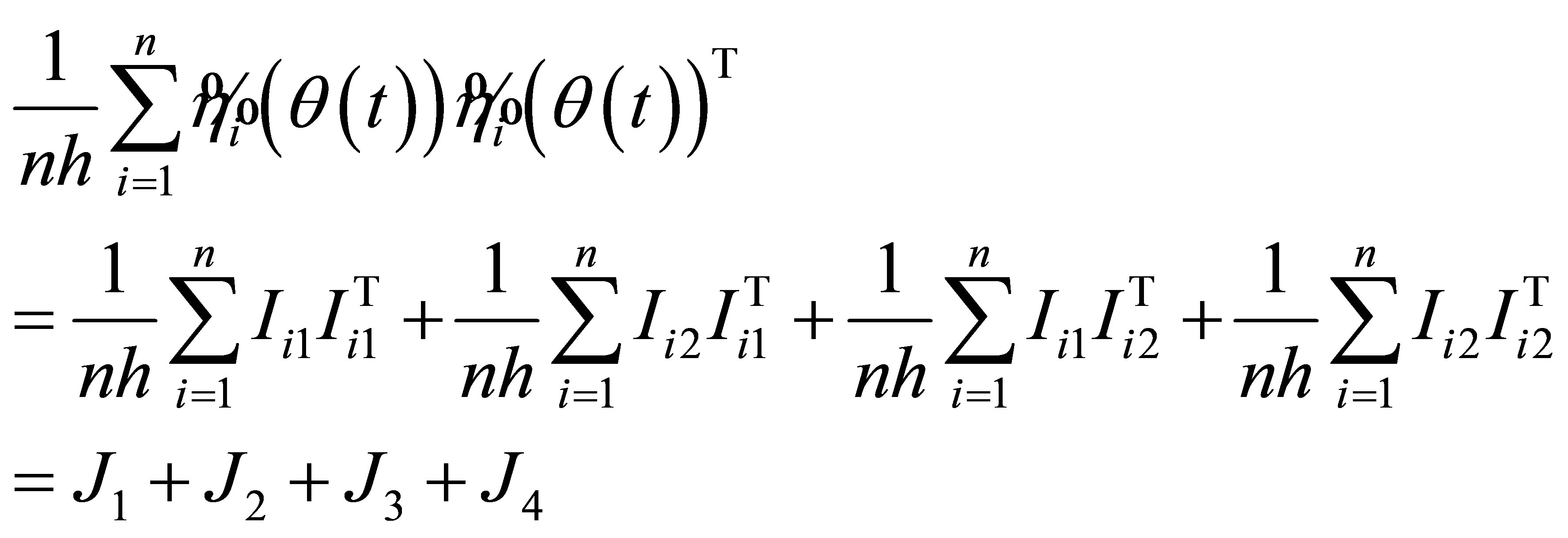
According to the proof of Lemma 4, we know that 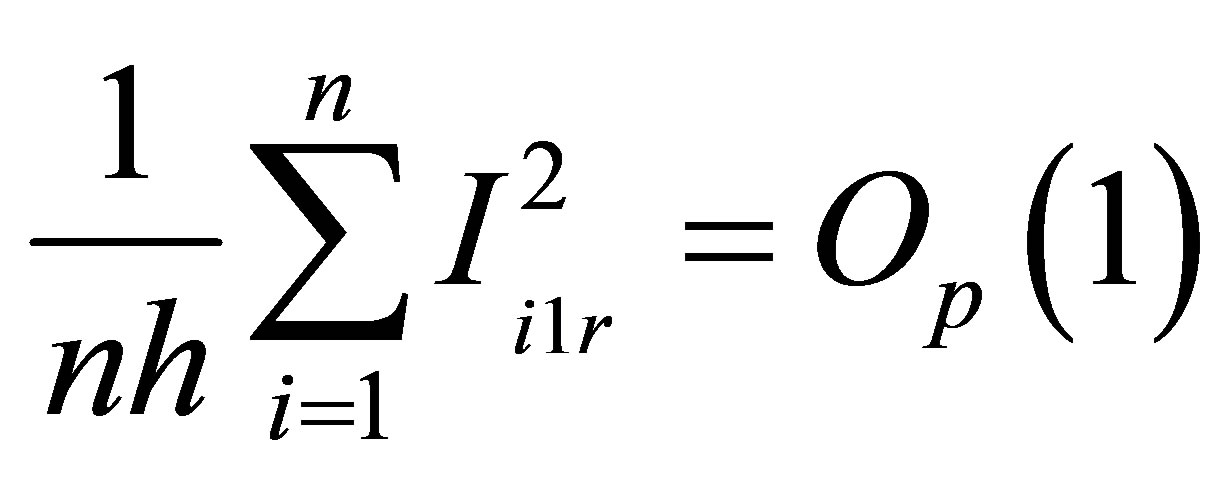 and
and 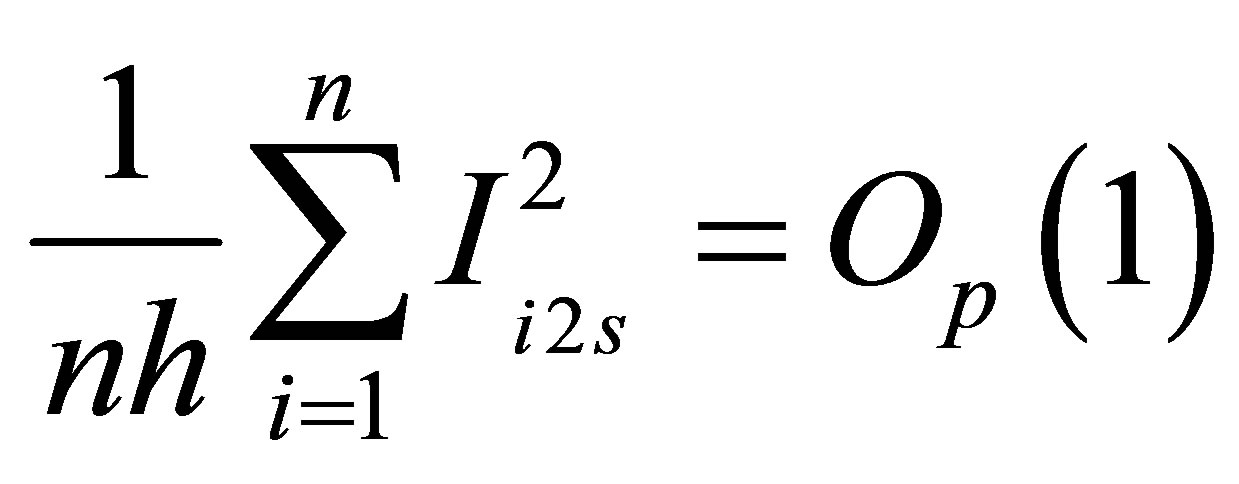 which are the rth or sth component of
which are the rth or sth component of 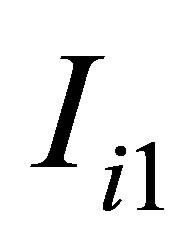 and
and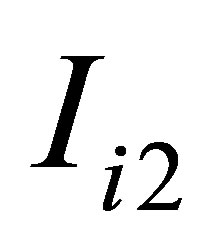 . Some simple algebra calculation leads to that
. Some simple algebra calculation leads to that . And we can derive
. And we can derive 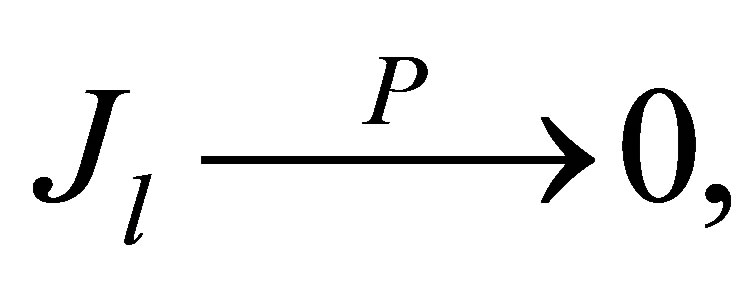
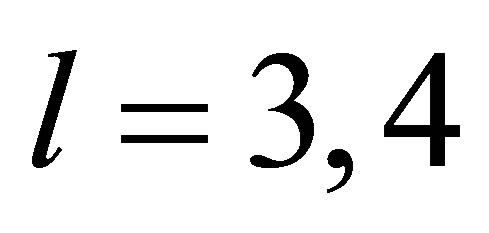 . Moreover, by the law of large numbers, we can derive that
. Moreover, by the law of large numbers, we can derive that . So, the proof of Lemma 5 is completed.
. So, the proof of Lemma 5 is completed.
Proof of Theorem 1. By the definition,  can be written a
can be written a
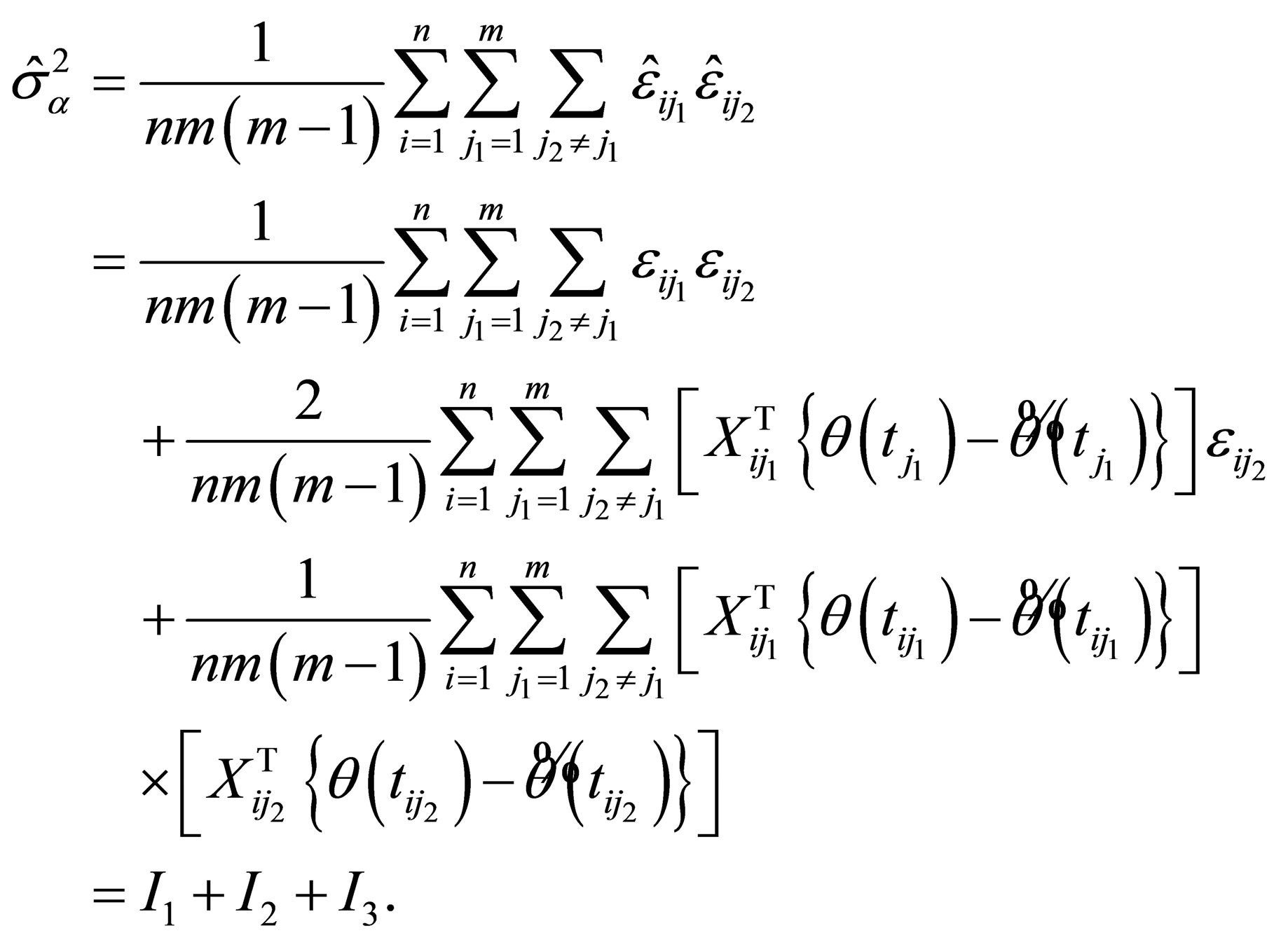
Using the Taylor formula and Lemma 1, we can derive 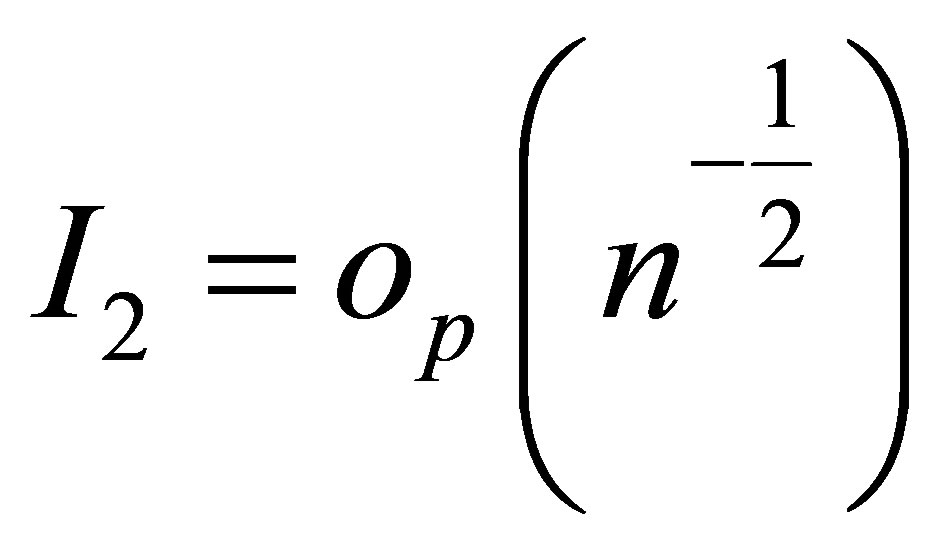 and
and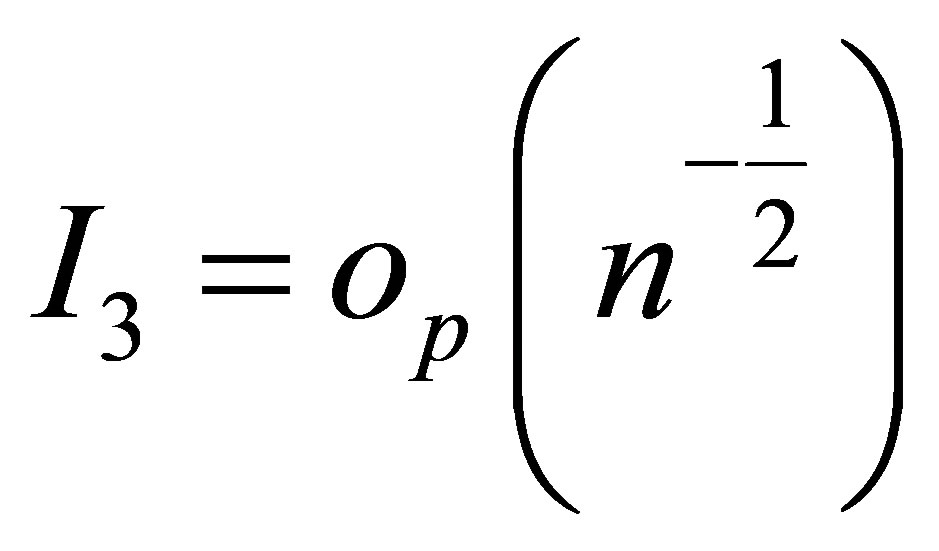 .
.
Moreover, by the Lyapunov central limit theorem and that proof of Theorem 4 in [8], we can dirive (14) in Theorem 1.
By the proof of the first part, we can easily prove (15) in Theorem 1.
Proof of Theorem 2. Here, we mainly provide the proof procedure by showing the evidence about the asymptotic equivalence between the auxiliary random vector (4) and that one (12) with the within-subject covariance being replaced by the estimator (11). That is the error caused by the use of plug-in estimation is negligible.
For the given estimator (11) for the within-subject covariance, the auxiliary random vector is
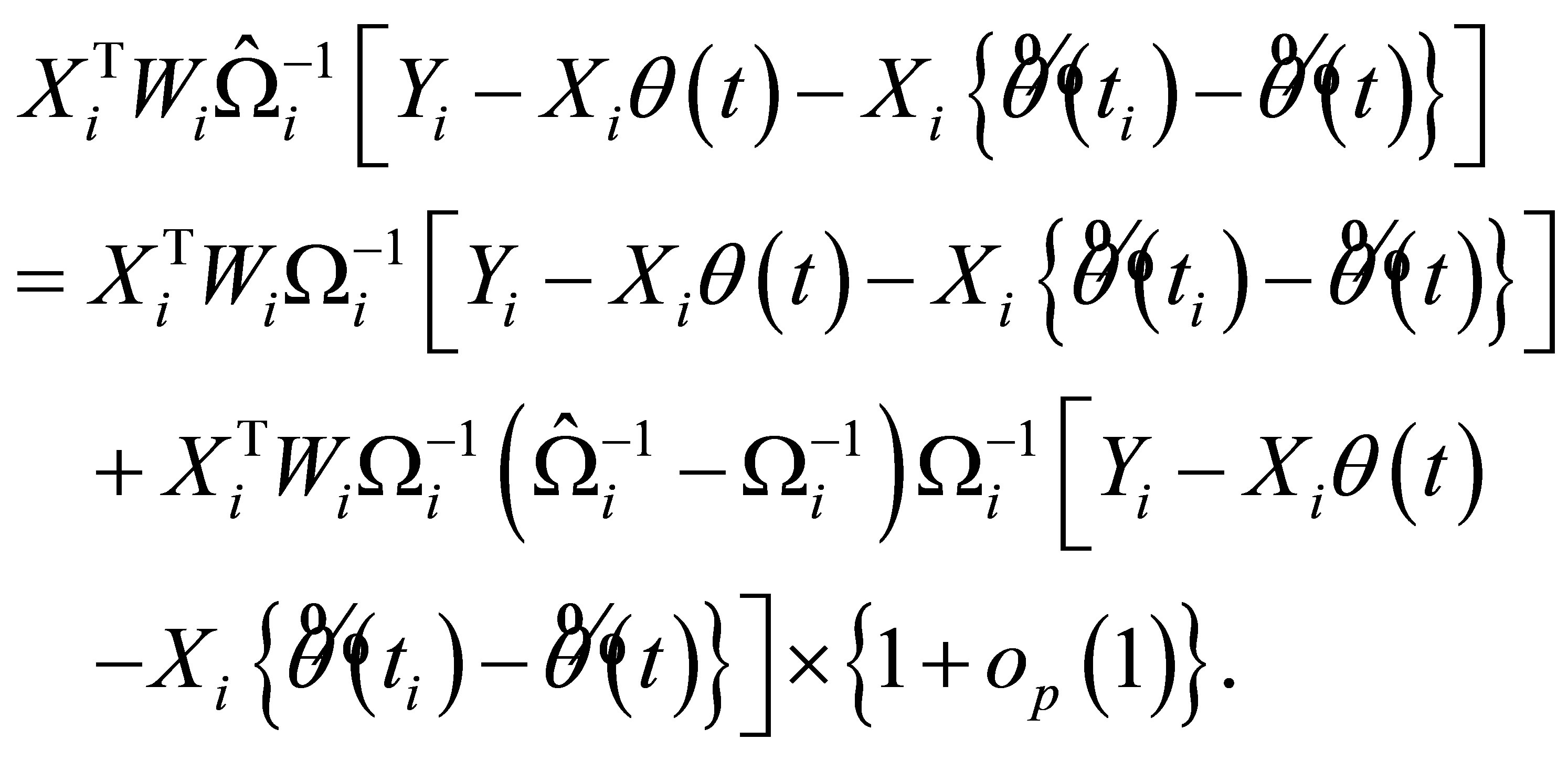 (A.4)
(A.4)
The second term in (A.4) is high order of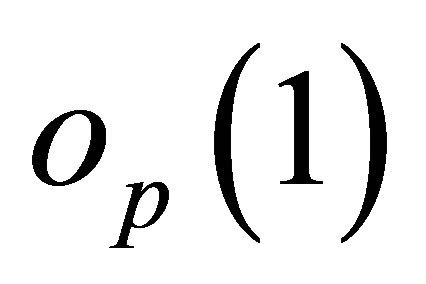 . Therefore, the empirical likelihood ratio based on the auxiliary random vector (12) with the estimated within subject covariance is asymptotic equivalent to that one (4) with a true one. By a Taylor expansion of (13) and following a similar lines as in the proof of Theorem (3.2) in [3], we can show that
. Therefore, the empirical likelihood ratio based on the auxiliary random vector (12) with the estimated within subject covariance is asymptotic equivalent to that one (4) with a true one. By a Taylor expansion of (13) and following a similar lines as in the proof of Theorem (3.2) in [3], we can show that 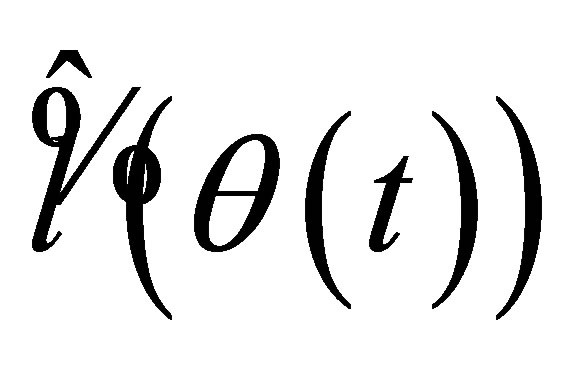 is asymptotic equivalent to that one (5) with the true covariance
is asymptotic equivalent to that one (5) with the true covariance
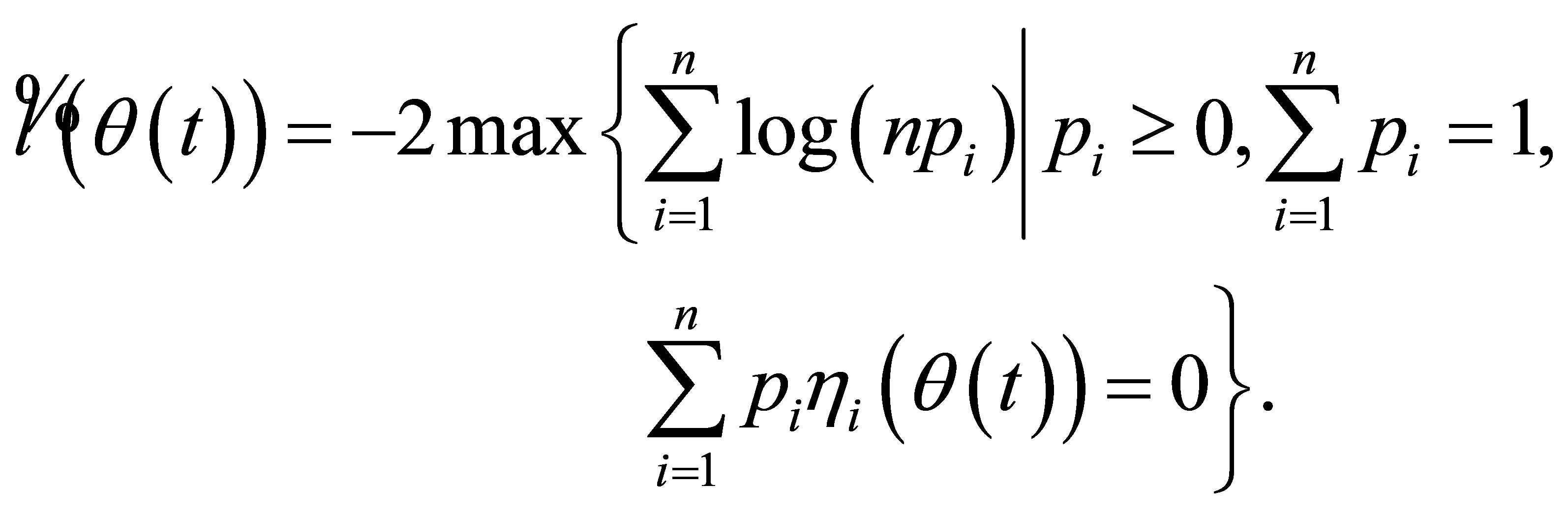
By the arguments in the proof of (2.14) in [11] and together with Lemma 3, we can derive that
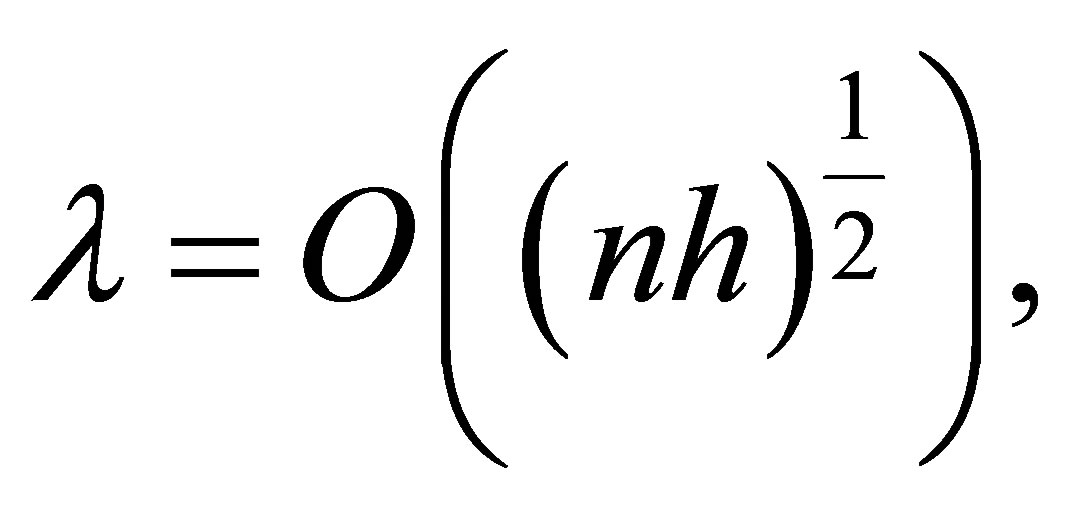 (A.5)
(A.5)
where  is defined by (7).
is defined by (7).
By Lemma 3-5 and (A.5), a Taylor expansion of (8) leads to
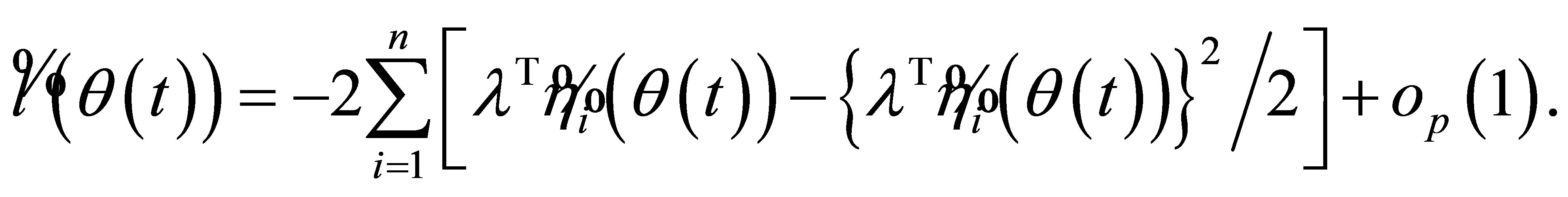 (A.6)
(A.6)
Then by (7), it follows that
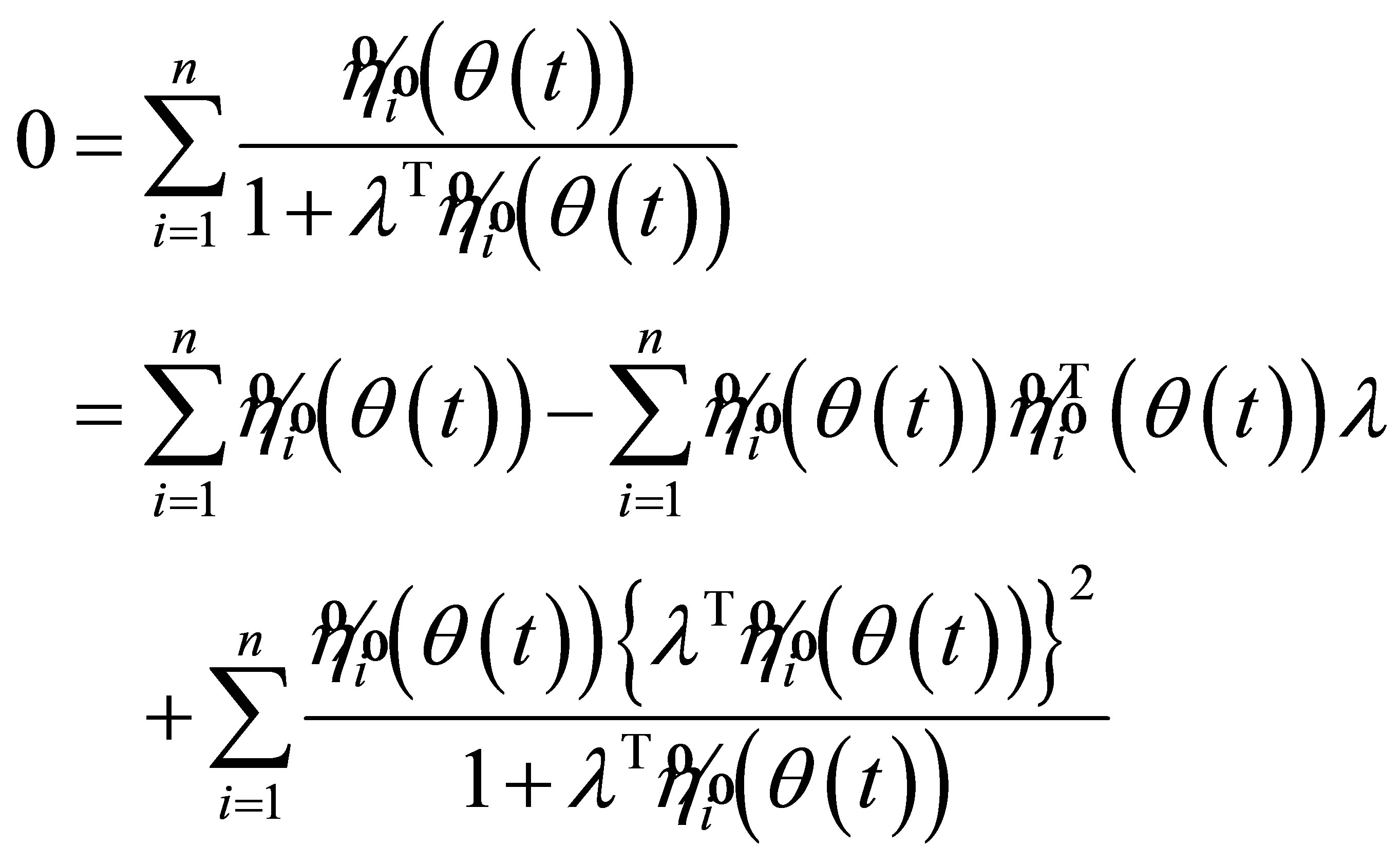 (A.7)
(A.7)
Hence, by Lemma 3-5, and (A.7), we can derive that
 (A.8)
(A.8)
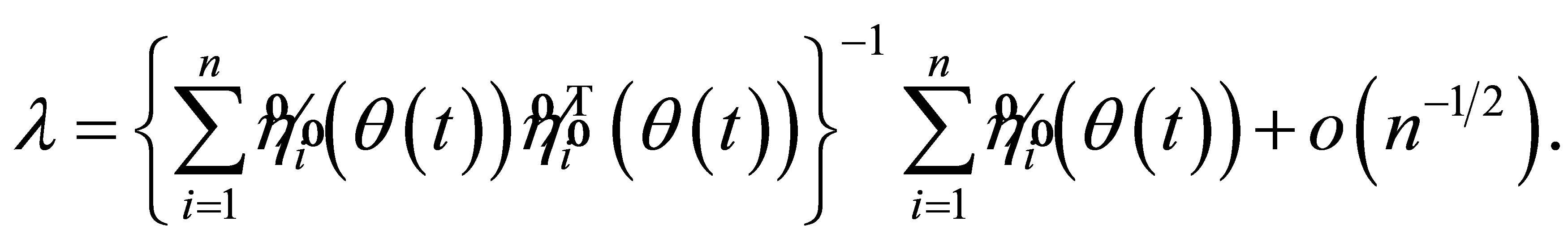 (A.9)
(A.9)
With the plug-in of (A.8) and (A.9) in (A.7), we can further derive that
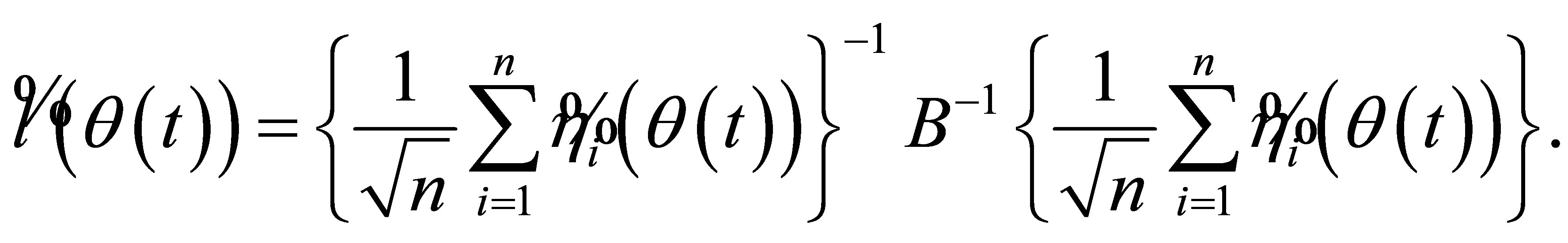 (A.10)
(A.10)
Therefore, the asymptotic result of Theorem 2 follows from Lemma 4 and 5.

