Open Journal of Statistics
Vol.4 No.1(2014), Article ID:42928,21 pages DOI:10.4236/ojs.2014.41006
Exchange Rate Market Sentiment Analysis of Major Global Currencies
K. S. Madhava Rao1*, Anjana Ramachandran2
1Department of Statistics, University of Botswana, Gaborone, Botswana
2Department of Mathematics, University of Botswana, Gaborone, Botswana
Email: *raom@mopipi.ub.bw
Copyright © 2014 K. S. Madhava Rao, Anjana Ramachandran. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property K. S. Madhava Rao, Anjana Ramachandran. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received September 16, 2013; revised October 16, 2013; accepted October 23, 2013
ABSTRACT
The paper deals with the analysis of market sentiments in exchange rates which are of great interest to trading individuals and institutional investors. For example, an institutional investor or a trading individual makes better investments and minimizes losses when equipped with an understanding of market sentiments in weekly or monthly exchange returns. In the approach suggested here, a typical market sentiment is defined on the basis of the certain function of the mean and the standard error of the logarithm of the ratio of successive daily exchange rates. Based on this surmise, the market sentiments are classified into various states, whereby states are defined according to the perceptions of the market player. A multinomial probability model is built to capture the uncertainties in market sentiments. Two asymptotically distribution-free tests, namely the chi-square and the likelihood ratio test of goodness of fit for the hypothesis of the symmetry in market sentiments are suggested. Two different measures of market sentiments are proposed. The approach advocated here will be of interest to researchers, exchange rate traders and financial analysts. As an application of the proposed line of approach, we analyze weekly market sentiments that govern exchange rates of the major global currencies—EUR, GBP, SDR, YEN, ZAR, USD, data from 2001-2012. Some interesting conclusions are revealed based on the data analysis.
Keywords: Chi-Square Tests; Exchange Rates; Market Sentiments; Weekly States
1. Introduction
The prevailing economic and political environment in the world has an impact on the international currency exchange rates. This gives a trader a strong and reliable tool to rate currencies combined with the analysis of data and charts. This helps the trader to make better investments and minimize losses. This paper essentially deals with a new method of defining and consequently analyzing market sentiments that govern exchange rates in particular and security prices and tradable options in general.
Most of the financial data analyses are focused on the prediction of the future prices of security and as such are model-based strategies. These are mainly geared to the needs of well-informed market players that include individual investors, financial institutions and mutual fund managers. It is widely believed that, security prices exhibit considerable variations from time to time and these variations can be objectively captured more or less by well-defined market volatility phenomena. The concept of volatility is imperative in the analysis of financial time series data. Broadly speaking, it is the unpredictable change of a variable over time. In the context of finance and economics, the volatility refers to the unstable states of economic and financial variables. These variables include stock prices, exchange rates, inflation rates, volume of trade, currency returns, etc. Generally speaking, the volatility could be defined as the changeability of the market trends. While, there are several definitions of the volatility; the common denominator in virtually all the definitions of volatility is variability. The difference nevertheless lies in how to measure this variability. The causes of volatility could be ascribed to several factors, such as local and global economic environments, maturity and delivery date of instrument, changes in trade volume, practices or patterns, new information among others. For a good description of definitions of the volatility and the causes of the volatility phenomena, we refer to [1].
1.1. Literature Review
The literature on economic and financial variable data analysis is quite extensive. Forecasts of the distribution of such variables are of great importance in the context of financial risk management. In pricing options, anticipated volatility over the life of the option is the crucial unknown parameter. One of the most popular tools used to explain volatility clustering in option pricing is the Auto Regressive Conditional Heteroscedasticity (ARCH) class of models. The ARCH model was invented by Engle [2]. The theoretical frame work of modeling volatility advocated by Engel captures the time-variability of the variance of returns by imposing an autoregressive structure on the conditional second moment of returns. Over the years there have been a number of extensions to the basic ARCH model. The most important of these is the generalized ARCH (or GARCH) model developed by Bollerslev [3] which includes lagged values of the conditional variance as extra regressors. Subsequently, many other ARCH-type processes have been developed to capture various dynamics. For additional references and expository studies using ARCH type of models and also for exhaustive theoretical treatment of volatility models, we refer to Blake [4] and Sheldon [5]. While sophisticated volatility estimation procedures, such as GARCH, are popular among finance researchers, these require econometrics software which is difficult for the average under-graduate student or casual options trader to obtain or master so have not found their way into most derivatives texts.
There have been several studies dealing with exchange rate volatility from an investor’s perceptive. For the sake of completeness, we outline a few of these, keeping in mind that none of these studies follow the approach that is advocated in this paper. Chung [6] discusses the relationship between the carry trade and exchange rate volatility from an investor’s perspective. In a carry trade, investors borrow in low-yield currencies and invest in high-yield currencies. In a scenario where the investor is aware of the risk posed by exchange rate depreciation, he considers methods to achieve predictable positive returns. The study considers three linear models—firstly, a model on lagged exchange rates, inflation and interest rate differentials; secondly, an extension of this model to include the purchasing power parity (PPP). Thirdly, PPP model is extended to include the lagged values of volatility proxy. Markiewicz [7] considers a time-varying link between exchange rates and the underlying fundamental macroeconomic variables that explains shifts in the volatility of exchange-rate returns. In this study given a model of the exchange rate, the coefficients of all possible combinations of the variables within this model are estimated. The most appropriate set of variables are used as a forecast of the future exchange rate. The impact of exchange rate volatility on real international trade flows is investigated empirically in [8]. The exchange rate volatility for the month ahead is computed from the intra-monthly variations in the exchange rate. The effect of exchange rate volatility on trade flows is found to be non-linear. The intra-month volatility of real exchange rate is evaluated from daily data.
Andersen et al. [9] discuss model-free estimates of daily exchange rate volatility and correlation using data on Deutschemark and Yen returns against the dollar. They establish that distributions of realized daily variances, standard deviations and covariances are found to be skewed to the right and leptokurtic while the distributions of logarithmic standard deviations and correlations are approximately Gaussian. Volatility movements are found to be highly correlated across the two exchange rates. In [10], Christiansen considers three risk measures to explain the FOREX excess returns for ten currencies, namely realized volatility, realized skewness, and value-at-risk. The inter-temporal risk-return trade-off of foreign exchange (FOREX) rates for ten currencies quoted against the USD is investigated. Monthly FOREX excess returns and risk measures calculated from daily observations are applied. The risk-return trade-off is contemporaneous for the currencies under investigation. There is no evidence of noncom temporaneous risk-return trade-off. Focus is also on the risk-return trade-off during the recent financial crisis where the risk-return trade-off becomes stronger.
The issues of exchange rate pass-through to domestic markets have been investigated extensively in [11]. The exchange rate pass-through (ERTP) can be divided into two main streams, with papers which focus on first step pass-through i.e., ERPT into import prices and second step pass-through i.e., ERPT into consumer prices. This study by O de Bandt et al [11] is a result of the concern caused by changes in institutional arrangements such as the introduction of euro area and to monetary and financial shocks. Estimating short and long run exchange rate pass through to import prices in countries that have adopted the euro currency is discussed. Time series and latest panel data techniques are used to test for cointegration; the relationship between import unit values, the exchange rate and foreign prices. The results allow for possible breaks around the formation of EMU. The euro appreciating from 2001 contributes to restoring a long run cointegration relationship.
Political factors are often cited as potential determinants of the nominal exchange rate [12]. However empirical exchange rate models seldom capture this influence. The study applies the Markov regime-switching model to identify regime switches for a sample of 25 countries over an 8-year time period. It uses the estimated transition probabilities obtained as observations for the dependent binary variable in a panel probit model, which included political risk as an independent variable. The study concludes that the political risk exerts a statistically significant concurrent effect on the nominal exchange rate.
Three models are compared for forecasting exchange rate [13]. Regression, Simple Naïve and ARIMA (an acronym for Autoregressive Integrated, and Moving Average) and focuses on finding the best model for forecasting exchange rate based on RMSE (Root Mean Square Error). The methods are combined with the lowest RMSE. The method has been applied to GB exchange rate with Iran.
The study in exchange rate risk management is conducted where, the Black-Scholes (BS) and Euler-Maruyama models (EMM) were tested on Indian Rupee (INR) and Malaysian Ringgit (MYR) rates of eight country currencies [14]. The study showed that though the principles differ, the trajectories of the two models forecast exchange rates that converge. The models proved to be inefficient testing on real Indian Rupee rates. In case of Malaysian Ringgit rates for almost six months, the models forecasted exchange rates with lesser error and their paths converge with the real rates. This study tests the Weiner process stochastic behaviour of exchange rates with real exchange rates. To find out the convergence and divergence, the real exchange rate is compared with Monte Carlo Simulated diffusion based BS and EMM. The errors shown by INR exchange rates are higher when compared to MYR. The results show that in case of INR these stochastic models produce lower rates than the actual exchange rates. Their path being significantly above the trajectories forecasted. In case of MYR all exchange rates, the BS and EMM converge for 6 months and diverges later. Hence these models can be applied for strong currencies and with some modifications for weak currencies.
1.2. Market Sentiment Approach
In this paper we advocate a new approach based on the market sentiments to analyse financial data rather than the traditional approach based on volatility measures. Market sentiment is the general prevailing attitude of investors to the anticipated price development in a market. This attitude is the accumulation of a variety of fundamental and technical factors, including price history, economic reports, seasonal factors, and national and world events. For example, if investors expect upward price movement in the stock market, the sentiment is said to be bullish. On the contrary, if the market sentiment is bearish, most investors expect downward price movement. Thus market sentiments may be construed as the manifestation of intense volatility into perceptible categories.
For the sake of clarity, we outline a few distinctions between volatility phenomenon and market sentiment. First of all, volatility is a continuous variable, while the market sentiment is invariably a categorical variable. Volatility is measured in terms of statistical concept of dispersion, while market sentiment is defined on the basis of a classification criterion. Volatility is the result of accumulation of a variety of fundamental and technical factors, including price history, economic reports, seasonal factors, and national, regional and global events. In general, the impact of volatility is perceived to be long term. On the other hand, market sentiments are even caused by extraneous and innocuous factors such as local geo-political events, quarterly company results, mergers and acquisitions, besides the factors that cause volatility. It is generally seen that impact of market sentiments are short term in nature and usually seen over weekly, monthly or quarterly data.
Forecasting market sentiments in financial data such as stock indices, volume of trade and currency returns is a formidable area of research in financial economics. There are innumerable causes, as mentioned earlier, that propel market sentiments in a financial data. To the best of our knowledge, no attempt seems to have been made to define market sentiments in precise quantitative terms and analyze those using statistical principles. The main contribution of this paper is therefore, to suggest an approach for modelling and related analysis of market sentiments.
Market sentiment is monitored with a variety of technical and statistical methods such as the number of advancing versus declining stocks and new highs versus new lows comparisons. A large share of overall movement of an individual stock has been attributed to market sentiment.
A simple market sentiment analysis that deals with daily trading series is the one based on the “pivotal theory”. In this analysis, current day’s market sentiment is arrived based on the pivot point which is simply defined as the average of high, low and closing prices. In a seven point system, the three sentiments above the pivot point sentiment are classified as “resistance 3” (= high + 2 (pivot-low)), “resistance 2” (= pivot + (high-low)) and “resistance 1” (= 2 pivot-low)). Similarly, the three sentiments below the pivot point sentiments are “support 1” (= 2 pivot-high)), “support 2” (= pivot-(high-low)) and “support 3” (= low-2 (high-pivot)). Similarly, in a five point pivot system one uses the previous day’s high, low and close, along with two support levels and two resistance levels to derive a pivot point. The internet portals of financial service providers and newspapers, world over, carry such investor friendly market sentiments for the prospective traders dealing with exchange rates, stocks and shares. Such market sentiments technical indicators are widely available on a day-to-day basis. While an indicator of market sentiments on a day-to-day basis has its own advantages and limitations, there seems to be very little work done on extending these ideas to capture market sentiments based on weekly and monthly data. The need for studying market sentiments based on the weekly and monthly data are many fold. For example, weekly and monthly sentiments are more stable and provide decisive clues as how the market is responding to the economic variables of interest. Further, they also indicate when to trade and what securities to trade with.
1.3. Preliminaries
Suppose that we are interested in the price of some security; such as exchange rate, stock price; interest rate, as it evolves over time. Let the present time be 0, and let 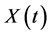 denote the price of the security at a time
denote the price of the security at a time ![]() from the present. Considerable work has been done over the years to analyze the time series data
from the present. Considerable work has been done over the years to analyze the time series data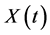 . The traditional approach is to assume a stochastic model for
. The traditional approach is to assume a stochastic model for 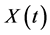 and engage in related inferential problems such as point and interval estimation and tests of hypotheses about the model parameters. For example, in the context of financial data analysis, many researchers have assumed that
and engage in related inferential problems such as point and interval estimation and tests of hypotheses about the model parameters. For example, in the context of financial data analysis, many researchers have assumed that  follows either a Brownian motion model or a geometric Brownian motion model, among others alternative models of interest. We say that the collection of prices
follows either a Brownian motion model or a geometric Brownian motion model, among others alternative models of interest. We say that the collection of prices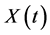 ,
,  , follows a Brownian motion with drift parameter
, follows a Brownian motion with drift parameter ![]() and variance parameter
and variance parameter 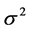 if, for all nonnegative values of
if, for all nonnegative values of ![]() and
and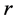 , the random variable
, the random variable  is independent of all prices up to time
is independent of all prices up to time ![]() and in addition, is a normal random variable with mean
and in addition, is a normal random variable with mean  and variance
and variance . On the other hand, the geometric Brownian motion is characterized by the fact that the random variable
. On the other hand, the geometric Brownian motion is characterized by the fact that the random variable  is independent of all prices up to time
is independent of all prices up to time![]() ; and if in addition,
; and if in addition, 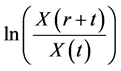 is a normal random variable with mean
is a normal random variable with mean 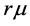 and variance
and variance . The properties, scope and suitability of these two models have been well discussed by many researchers and are well documented in standard reference books; see for example [15]. In the study proposed here our focus will be on the geometric Brownian motion model and accordingly we deal with the random variable
. The properties, scope and suitability of these two models have been well discussed by many researchers and are well documented in standard reference books; see for example [15]. In the study proposed here our focus will be on the geometric Brownian motion model and accordingly we deal with the random variable
 rather than the
rather than the ’s.
’s.
The present study focuses on the exchange rates of six currencies against the currency of Botswana Pula (BWP). The exchange rates data were drawn from the Bank of Botswana’s Botswana Financial Statistics database. The six currencies considered in the analysis are Euro (EUR), British Pound (GBP), Special Drawing Rights (SDR), Japanese Yen (YEN), South African Rand (ZAR) and US Dollar (USD). All the exchange rates have been quoted in terms of Botswana Pula. The time series data refers to the working day exchange rates of the six stated currencies for 12 years starting from 2001 and ending with 2012. The data considered for the analysis here refer to the logarithm of the ratio of the day’s exchange rate  with the previous day’s exchange rate
with the previous day’s exchange rate
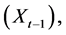 i.e.,
i.e.,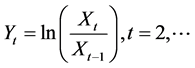 . Then it is well known that
. Then it is well known that 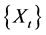 follows the geometric Brownian motion.
follows the geometric Brownian motion.
In Section 2, market sentiments are defined on the basis of certain classification rules that depend on the mean and standard deviation of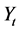 . Three classification rules which reflect market sentiments are proposed. Section 3, lists the assumptions and the derivation of the associated multinomial model that appropriately describes different market sentiments. In particular, seven state and five state symmetric market sentiment models are constructed. The computation of such joint probabilities is a reliable guide to the investor. In Section 4, two non-parametric tests for testing the goodness of fit of symmetric market sentiment model are carried out. Section 5 proposes two measures of drift in market sentiments for the multinomial model. In Section 6, certain rules to measure the significance of market sentiment states are formulated. It is followed by the application of the proposed methodology to analyse weekly market sentiments in exchange rates of six global currencies in Section 7. Section 8 concludes the paper.
. Three classification rules which reflect market sentiments are proposed. Section 3, lists the assumptions and the derivation of the associated multinomial model that appropriately describes different market sentiments. In particular, seven state and five state symmetric market sentiment models are constructed. The computation of such joint probabilities is a reliable guide to the investor. In Section 4, two non-parametric tests for testing the goodness of fit of symmetric market sentiment model are carried out. Section 5 proposes two measures of drift in market sentiments for the multinomial model. In Section 6, certain rules to measure the significance of market sentiment states are formulated. It is followed by the application of the proposed methodology to analyse weekly market sentiments in exchange rates of six global currencies in Section 7. Section 8 concludes the paper.
2. Market Sentiment Constructs
Consider a financial market where the time series data related to exchange rates of major global currencies is available on a day to day basis. We shall propose a classification rule for defining market sentiments for the weekly means of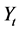 ’s.
’s.
The notation used in the paper is as follows: “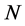 ”—total number of days in a study period, “
”—total number of days in a study period, “![]() ”—refers to the day, “
”—refers to the day, “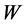 ”—total number of weeks in a study period, “
”—total number of weeks in a study period, “![]() ”—refers to the week,
”—refers to the week,  ,
,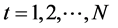 —the exchange rate at time “
—the exchange rate at time “![]() ”, “
”, “ ”—denotes the number of business days in a week. Here,
”—denotes the number of business days in a week. Here,  varies between 1 and 5 in a typical FOREX market. Table 1 displays the time series data related to daily exchange rate
varies between 1 and 5 in a typical FOREX market. Table 1 displays the time series data related to daily exchange rate 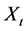 and
and

Let the average of , for the week
, for the week 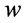 be given by
be given by
 , (1)
, (1)
and the variance of , for the week
, for the week 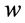 be given by
be given by
 (2)
(2)
Then under the assumption of geometric Brownian motion, it follows that  are independent and identically distributed normal variables with mean and variance given by,
are independent and identically distributed normal variables with mean and variance given by,  and
and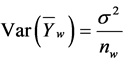 . Furtherit follows that the standardized variate
. Furtherit follows that the standardized variate 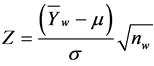 has
has 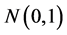 distribution. Therefore statistic
distribution. Therefore statistic ![]() can be used to define appropriate classification rules for the market sentiments. Furthermore, by virtue of the symmetry of
can be used to define appropriate classification rules for the market sentiments. Furthermore, by virtue of the symmetry of![]() , the market sentiment states based on
, the market sentiment states based on ![]() would be symmetric around the centre of the distribution of means. Accordingly, from the vantage point of a seller in a FOREX market, we define the following mutually exclusive and collectively exhaustive states.
would be symmetric around the centre of the distribution of means. Accordingly, from the vantage point of a seller in a FOREX market, we define the following mutually exclusive and collectively exhaustive states.
![]() : The dread sentiment. In this state, the exchange rate witnesses a sharp fall. The gloomy sentiment causes the trader to sell his currency. The players in the market may face bankruptcy or regulatory intervention. The FOREX market may cease to be profitable.
: The dread sentiment. In this state, the exchange rate witnesses a sharp fall. The gloomy sentiment causes the trader to sell his currency. The players in the market may face bankruptcy or regulatory intervention. The FOREX market may cease to be profitable.
 : The bearish sentiment. This state is indicative by the marked downward trend of the exchange rate. This causes frustration to a trader dealing in FOREX. This may result in selling of FOREX and undermine trader confidence. The FOREX market may seem to be an unattractive investment option.
: The bearish sentiment. This state is indicative by the marked downward trend of the exchange rate. This causes frustration to a trader dealing in FOREX. This may result in selling of FOREX and undermine trader confidence. The FOREX market may seem to be an unattractive investment option.
 : The decline sentiment. In this state the exchange rate witnesses a moderate fall, setting off the panic button to traders. Again, the trader’s confidence is jolted.
: The decline sentiment. In this state the exchange rate witnesses a moderate fall, setting off the panic button to traders. Again, the trader’s confidence is jolted.
 : The calm sentiment. This state is suggestive of normal activity. The trader is not agitated and continues to be an active player in the FOREX market.
: The calm sentiment. This state is suggestive of normal activity. The trader is not agitated and continues to be an active player in the FOREX market.
Table 1. Daily exchange rates.
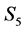 : The incline sentiment. This state gives a perception of hope to the trader. The exchange rate witnesses a moderate upward swing. The FOREX market may seem to be an attractive investment option.
: The incline sentiment. This state gives a perception of hope to the trader. The exchange rate witnesses a moderate upward swing. The FOREX market may seem to be an attractive investment option.
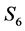 : The bullish sentiment. This state is indicative by the marked upward swing, triggering speculation by a trader of FOREX. The FOREX market may be perceived to be profitable.
: The bullish sentiment. This state is indicative by the marked upward swing, triggering speculation by a trader of FOREX. The FOREX market may be perceived to be profitable.
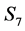 : The greed sentiment. This is a state in which the exchange rate witnesses a sharp rise, encouraging the trader to sell, thereby making a profit or wait, hoping to have his investment appreciate. FOREX market will seem to be a good investment option.
: The greed sentiment. This is a state in which the exchange rate witnesses a sharp rise, encouraging the trader to sell, thereby making a profit or wait, hoping to have his investment appreciate. FOREX market will seem to be a good investment option.
It may be pointed out that states  and
and  reflect smiling sentiments with varying degree while, states
reflect smiling sentiments with varying degree while, states 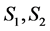 and
and 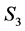 reflect frowning sentiments with varying degree. In order to reflect these seven symmetric market sentiments, we associate the following classification rules, based on the statistic
reflect frowning sentiments with varying degree. In order to reflect these seven symmetric market sentiments, we associate the following classification rules, based on the statistic![]() , with the states
, with the states![]() . Let
. Let ![]() denote an estimate of
denote an estimate of![]() , say;
, say; , the weekly average of logarithm of ratios of exchange rates and
, the weekly average of logarithm of ratios of exchange rates and 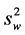 be a consistent estimateof
be a consistent estimateof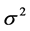 .
.
Then for a week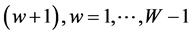 , the weekly sentiment of exchange rate is said to belong to 1) State
, the weekly sentiment of exchange rate is said to belong to 1) State![]() , if
, if 
2) State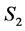 , if
, if 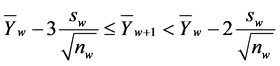
3) State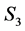 , if
, if 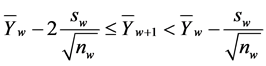
4) State , if
, if
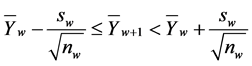 (3)
(3)
5) State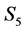 , if
, if 
6) State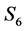 , if
, if 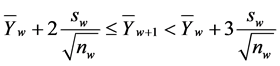
7) State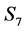 , if
, if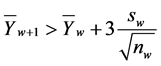 .
.
In the classification rule (3), the multipliers ±3 and ±2 of 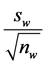 are analogous to “action and warning limits”
are analogous to “action and warning limits”
commonly used in statistical process control [16]. In the context of the present study; they indicate the magnitude and direction in which one state is distinguished from another. The class of states  suggested here is commonly perceived in an active FOREX market economy. In a less speculative or infrequently traded FOREX market economy, some states can be merged as follows:
suggested here is commonly perceived in an active FOREX market economy. In a less speculative or infrequently traded FOREX market economy, some states can be merged as follows:
1) Form a new state , if
, if

Note that states  in
in  are combined to form the state
are combined to form the state 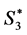 and accordingly we have five-state model
and accordingly we have five-state model . Here,
. Here,  maybe called an “oscillating” or “uncertain” state.
maybe called an “oscillating” or “uncertain” state.
2) Form two new states 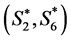 from the merging states
from the merging states 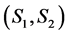 of
of  into
into 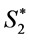 and states
and states  of
of 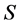 into
into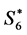 .
.
The new merged states may be called “bearish” and “bullish” respectively. The five-state model in this case would be 
Alternative Rules of Classification
The states can be redefined on the basis of quartiles, if the market sentiments appear to be equally spread over four categories. Then the multipliers of  can be taken to be the three quartiles of the standard normal distribution
can be taken to be the three quartiles of the standard normal distribution . Accordingly, for a week
. Accordingly, for a week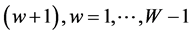 , the weekly exchange rate sentiment is said to belong to 1) State
, the weekly exchange rate sentiment is said to belong to 1) State![]() , if
, if 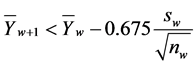
2) State , if
, if
 (4)
(4)
3) State , if
, if 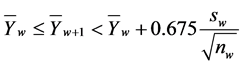
4) State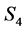 , if
, if 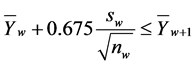
The sentiments expressed by the four states may be referred to as follows:
![]() : “grim bearishness”,
: “grim bearishness”,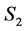 : “downbeat”,
: “downbeat”,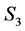 : “upbeat”,
: “upbeat”,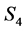 : “zestful bullishness”.
: “zestful bullishness”.
Alternatively, the states can be redefined on the basis of deciles, for example, if it is perceived that the middle 40% of the distribution of log ratio of exchange rates equally correspond to four core market sentiments. In this case, the multipliers of 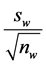 may be taken to correspond to the five deciles, namely,
may be taken to correspond to the five deciles, namely, 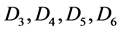 and
and 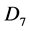
of the standard normal distribution (
 ). The classification rule for these six states then would be as follows:
). The classification rule for these six states then would be as follows:
For a week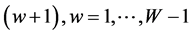 , the weekly sentiment of exchange rate is said to belong to 1) State
, the weekly sentiment of exchange rate is said to belong to 1) State![]() , if
, if 
2) State , if
, if
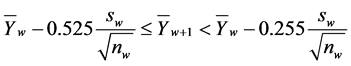
3) State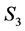 , if
, if
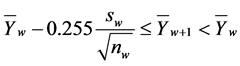 (5)
(5)
4) State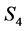 , if
, if 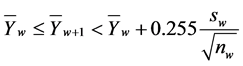
5) State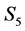 , if
, if

6) State , if
, if 
In the classification rule (5), the six market sentiments states may be suitably named depending on sellers’ perceptions.
3. A Probability Model for Market Sentiments
From the classical probability viewpoint, different states of market sentiments quite naturally lend themselves to be modelled into a suitable probability model. Thus, occurrences of wide swings, for example, in daily, weekly or monthly exchange rates can be viewed as states of market sentiments and therefore can be analyzed in terms of probability model based approach. The multinomial model that describes different market sentiment states is possibly a natural model that suits best under the circumstance and is based on the following assumptions.
A.1: The exchange rates are available for all working days of the FOREX market.
A.2: The exchange rates are subject to random shocks due to the market environment.
A.3: The wide swings in weekly exchange rates readily translate into market sentiments.
A.4: The market sentiment states are symmetric.
A.5: The exchange rates are analyzed from the perspective of a seller.
Given the time series data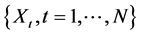 , transformed data
, transformed data  and the classification rule, the weekly exchange rates
and the classification rule, the weekly exchange rates 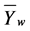 can be assigned to k suitably defined mutually exclusive and exhaustive states,
can be assigned to k suitably defined mutually exclusive and exhaustive states,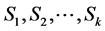 . Also, let the probability that a typical weekly average
. Also, let the probability that a typical weekly average 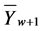 belongs to the state
belongs to the state 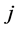 for
for , be denoted by
, be denoted by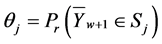 . Let
. Let ![]() denote the number of occurrences of the state
denote the number of occurrences of the state ![]() in an independent sequence of the phenomena observed for
in an independent sequence of the phenomena observed for  weeks. Then the vector
weeks. Then the vector  follows a multinomial distribution [17] with the joint probability mass function (p.m.f.) given by
follows a multinomial distribution [17] with the joint probability mass function (p.m.f.) given by
 (6)
(6)
for all 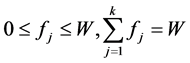 and
and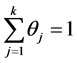 .
.
In general, the parameters![]() ’s in the model given by (6) are unknown and can be estimated by their empirical estimates
’s in the model given by (6) are unknown and can be estimated by their empirical estimates
 (7)
(7)
Under the assumption of multinomial probability model, it can be shown that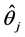 ’s are in fact the unrestricted maximum likelihood estimators of
’s are in fact the unrestricted maximum likelihood estimators of![]() .
.
3.1. A Symmetric Seven States Market Sentiment Model
Classifying each week’s exchange rates based on the rule (3) defined earlier; the required multinomial distribution model for the market sentiment is given by,
 (8)
(8)
for all  and
and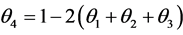 .
.
It can be shown that the restricted maximum likelihood estimators of the parameters in the model given by (8) are given by
 (9)
(9)
3.2. A Symmetric Five States Market Sentiment Model
For the class of states  described earlier, it can be shown that the corresponding multinomial model is given by
described earlier, it can be shown that the corresponding multinomial model is given by
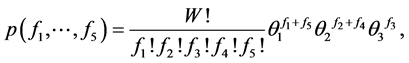 (10)
(10)
Further, the restricted maximum likelihood estimators of the parameters in the model (10) are given by
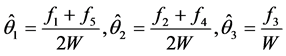 (11)
(11)
For the monthly exchange rates data, a multinomial model can be constructed using the same technique. The average and standard deviations of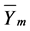 ’s will be computed based on the monthly data using an analogous classification rule.
’s will be computed based on the monthly data using an analogous classification rule.
The monthly average of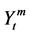 ’s for the month “
’s for the month “![]() ” is given by
” is given by
 (12)
(12)
and the corresponding variance is given by
 (13)
(13)
where, “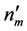 ”—denotes the total number of trading days in a month “
”—denotes the total number of trading days in a month “![]() ”,
”,  , “
, “![]() ” is the total number of months in the given exchange rate time series.
” is the total number of months in the given exchange rate time series.
To construct multinomial probability models for the other classification rules, the same technique can be utilized. For example, for the rule (4), 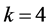 and for the rule (5),
and for the rule (5),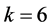 . Upon modelling the market sentiment states of exchange rates for the given time series data, joint probability of occurrence of a specific sequence of market sentiment states in the forthcoming weeks can be computed. The computation of such joint probabilities guides an investor to foray into forecasts based on weekly or monthly data. The trader has a clear direction with regard to FOREX operations i.e. to enter the market or make an exit.
. Upon modelling the market sentiment states of exchange rates for the given time series data, joint probability of occurrence of a specific sequence of market sentiment states in the forthcoming weeks can be computed. The computation of such joint probabilities guides an investor to foray into forecasts based on weekly or monthly data. The trader has a clear direction with regard to FOREX operations i.e. to enter the market or make an exit.
4. Tests for Symmetric Market Sentiment Model
In an equilibrium market, the locus of exchange rates is around the mean of exchange rates. Intermittent variations around the mean in the daily or weekly or monthly exchange rates are suggestive of non-symmetric drifts in market sentiments. A dense central part of the distribution of means would mean less non-symmetric drifts in market sentiments. Whereas a skewed exchange rate means cluster in the tail areas of the distribution of means would reflect a high degree of un-symmetric drifts in market sentiments. The hypothesis of absence of symmetric drift is characterized by the model given by (8) to an extent. Accordingly, the null and the alternative hypotheses of interest are
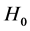 : The drift in exchange rate market sentiment regimes is characterized by the model (8)
: The drift in exchange rate market sentiment regimes is characterized by the model (8)
versus
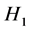 : The drift in exchange rate market sentiment regimes is not characterized by the model (8)
: The drift in exchange rate market sentiment regimes is not characterized by the model (8)
By virtue of the assumption of geometric Brownian motion, it follows that 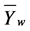 are i.i.d
are i.i.d 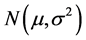 and therefore atest of
and therefore atest of 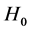 vs
vs 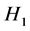 can be carried out in terms of Pearson’s chi-square test of goodness of fit. This test considers the magnitude of discrepancy between the observed and the expected frequency of weekly market sentiments. It is well known that the test requires the expected cell frequencies to be at least five. However, under the assumption of normality, tail probabilities in the first two and the last two market sentiment intervals defined by the classification rule (3) being very small, will likely to result in expected frequencies being less than five. This would necessitate merging of classes, and therefore may fail to truly discriminate between the null and alternative hypotheses being tested. Therefore, we resort to test
can be carried out in terms of Pearson’s chi-square test of goodness of fit. This test considers the magnitude of discrepancy between the observed and the expected frequency of weekly market sentiments. It is well known that the test requires the expected cell frequencies to be at least five. However, under the assumption of normality, tail probabilities in the first two and the last two market sentiment intervals defined by the classification rule (3) being very small, will likely to result in expected frequencies being less than five. This would necessitate merging of classes, and therefore may fail to truly discriminate between the null and alternative hypotheses being tested. Therefore, we resort to test  versus
versus 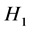 based on the symmetric multinomial model discussed earlier. The tests are proposed based on the criteria of Pearson Chi-Square and the generalized Likelihood Ratio of goodness of fit [18]. It can be shown that if the weekly/monthly exchange rates do not exhibit any form of non-symmetric drift, then the model given by (6) with
based on the symmetric multinomial model discussed earlier. The tests are proposed based on the criteria of Pearson Chi-Square and the generalized Likelihood Ratio of goodness of fit [18]. It can be shown that if the weekly/monthly exchange rates do not exhibit any form of non-symmetric drift, then the model given by (6) with , should reduce to the model given by (8) where
, should reduce to the model given by (8) where 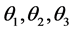 and
and  satisfy the restriction
satisfy the restriction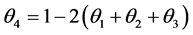 . Further, it can be shown that the Pearson Chi-Square test statistic for testing
. Further, it can be shown that the Pearson Chi-Square test statistic for testing ![]() vs
vs  in the model (8) is given by
in the model (8) is given by
 (14)
(14)
The decision rule is to reject![]() , at a level of significance
, at a level of significance![]() , in favour of
, in favour of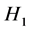 , if the calculated
, if the calculated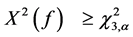 , where
, where  is the upper
is the upper ![]() percentile of a Chi-Square distribution with 3 degrees of freedom.
percentile of a Chi-Square distribution with 3 degrees of freedom.
Instead of the Chi-Square test of goodness of fit, one may use the likelihood ratio test to test 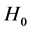 vs
vs . Accordingly, it can be shown that, the likelihood ratio test statistic [18] for testing the model (6) versus the model (8) is given by
. Accordingly, it can be shown that, the likelihood ratio test statistic [18] for testing the model (6) versus the model (8) is given by
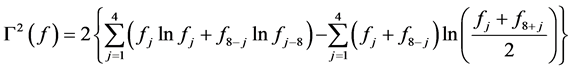 (15)
(15)
The decision rule is to reject , at level of significance
, at level of significance![]() , in favour of
, in favour of , if the calculated
, if the calculated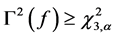 , where
, where  is the upper
is the upper ![]() percentile of a Chi-Square distribution with 3 degrees of freedom.
percentile of a Chi-Square distribution with 3 degrees of freedom.
5. Measures of Drift in Market Sentiments
A measure of drift in market sentiments is a pointer to variations in the states of market sentiments of exchange rate regimes either over the time scales or the currency portfolios. Based on the discussions in the previous Section, we propose two indicators of market sentiments for the multinomial model given by (8). The first measure utilizes the idea advocated by the classical chi-square measure of discrepancy between the observed and the expected counts. It is given by
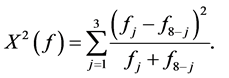 (16)
(16)
The second measure is based on the likelihood ratio principle. The likelihood function is a sufficient summary of sample information, and the likelihood principle [18] says that inferences should be based on likelihood functions. When there are competing models, say  and
and 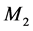 as possible explanations of a set of data, the likelihood approach is to compare their likelihoods,
as possible explanations of a set of data, the likelihood approach is to compare their likelihoods,  and
and . Intuition suggests that we should prefer the explanation offered by
. Intuition suggests that we should prefer the explanation offered by  when the likelyhood ratio
when the likelyhood ratio 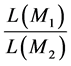 is small—when
is small—when  is much more “likely” than
is much more “likely” than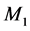 . It can be shown that for the models (6) and (8), the measure based on the likelihood ratio principle is given by
. It can be shown that for the models (6) and (8), the measure based on the likelihood ratio principle is given by
 (17)
(17)
It is easy to see that  and
and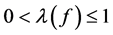 . Intuitively, small values of
. Intuitively, small values of 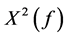 indicates that the model (8) is likely, while values of
indicates that the model (8) is likely, while values of 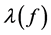 close to 1 indicates that the model (8) is likely than model (6). If
close to 1 indicates that the model (8) is likely than model (6). If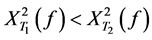 , for two periods of time
, for two periods of time 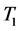 and
and![]() , then the exchange rates during the period
, then the exchange rates during the period  exhibits lesser drift than during the period
exhibits lesser drift than during the period  The measure given by (17) can be similarly used to make comparisons across either two or more periods of time or two or more currency portfolios.
The measure given by (17) can be similarly used to make comparisons across either two or more periods of time or two or more currency portfolios.
A variant of the measure (16) can be used to ascertain the direction of market sentiments especially when the hypothesis of symmetric market sentiments is rejected. For example, one may use the measure
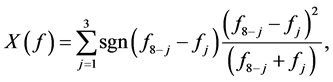 (18)
(18)
where,  is the sign function defined by
is the sign function defined by 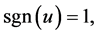 if
if , if
, if 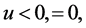 otherwise. A large positive
otherwise. A large positive 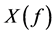 would indicate smiling sentiment states while a large negative
would indicate smiling sentiment states while a large negative 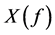 would indicate frowning sentiments.
would indicate frowning sentiments.
6. Significance of Market Sentiment States
We may remark that complying with a non-informative classification rule; each classified state will have an equal probability. Following this view point, certain rules to measure the significance of market sentiment states may be formulated. To start with, some rules can be devised using suitable factor of .We propose the following definitions that specify the criteria of assessing the significance of one or a set of market sentiment states. It is assumed that each market sentiment state has a positive probability based on a certain classification rule.
.We propose the following definitions that specify the criteria of assessing the significance of one or a set of market sentiment states. It is assumed that each market sentiment state has a positive probability based on a certain classification rule.
Definition 1: Let there be “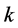 ”
”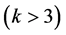 states,
states, . Then based on the empirical evidence
. Then based on the empirical evidence , a state
, a state , is said to be 1) Weakly Persistent if
, is said to be 1) Weakly Persistent if

2) Moderately Persistent if

3) Strongly Persistent if
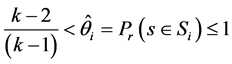
Definition 2: Let there be “ ”
” states,
states, . Let
. Let ![]() be the class of all states of a specific type given by Definition (1).
be the class of all states of a specific type given by Definition (1).
Then a set of similar states
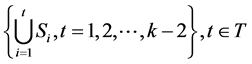 .
.
is said to be 1) Weakly Persistent if
 2) Moderately Persistent if
2) Moderately Persistent if
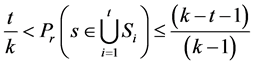
3) Strongly Persistent if

The definition of persistency of a single state or collection of states aids the profit earning motive of a prospective seller of FOREX. A trader decides, based on these criteria, to regulate his funds by investing among different portfolios which are expected to yield good returns in a short as well as a long period of time. As a rule of thumb, a strongly persistent state may indicate that a market is upbeat or down beat, while a moderately persistent state may mean an investment – return friendly. However, a weekly persistent state may be considered to be an unfriendly environment. To put it differently, strongly persistent states, moderately persistent states and weakly persistent states are those sentiment states which are more often, often and less often frequented in that order.
7. Applications to Major Global Currencies’ Market Sentiments
The daily FOREX data were drawn from the Bank of Botswana’s Botswana Financial Statistics database. The six currencies considered for the purpose of analysis are Euro (EUR), Great Britain Pound (GBP), Special Drawing Rights (SDR), Japanese Yen (YEN), South African Rand (ZAR) and United States Dollar(USD). The data considered is for a 12 year period from Jan 2001 to December 2012. For the purpose of weekly analysis, we calculated,  , the logarithm of the ratio
, the logarithm of the ratio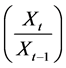 , where
, where 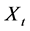 is the day’s exchange rate and
is the day’s exchange rate and 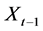
is the previous day’s exchange rate. Figure 1 shows the plot of weekly average of ![]() for the six currencies during the years 2001-2012. The line graphs exhibit quite significant variations on the log scale and these variations are devoid of any meaningful comparisons and interpretations. The plots of time series data per se do not help to reveal the presence of market sentiments except the presence of significant variations in log returns.
for the six currencies during the years 2001-2012. The line graphs exhibit quite significant variations on the log scale and these variations are devoid of any meaningful comparisons and interpretations. The plots of time series data per se do not help to reveal the presence of market sentiments except the presence of significant variations in log returns.
Next, we classify movements in weekly exchange rate log return means into seven market sentiment states  using the classification rule (3) outlined in Section 2. The basic data considered is the weekly means of log returns of the six currencies for the years 2001 to 2012. The Excel software based computations that lead to the market sentiment states are omitted and can be obtained from the first author. Table 2 shows weekly FOREX sentiments of the six currencies for years 2001-2012.
using the classification rule (3) outlined in Section 2. The basic data considered is the weekly means of log returns of the six currencies for the years 2001 to 2012. The Excel software based computations that lead to the market sentiment states are omitted and can be obtained from the first author. Table 2 shows weekly FOREX sentiments of the six currencies for years 2001-2012.
Figure 2 shows weekly FOREX sentiments of the six currencies for years 2001-2012. Each bar in a year refers to the market sentiments ![]() to
to  in that order. The height of bars refers to weekly frequency of market sentiments in each year. From the Figure 2 it is seen that all the six currencies show different levels of drifts in market sentiments over the years. However, it is difficult to ascertain the symmetry of market sentiments in each of the years for the six currencies considered.
in that order. The height of bars refers to weekly frequency of market sentiments in each year. From the Figure 2 it is seen that all the six currencies show different levels of drifts in market sentiments over the years. However, it is difficult to ascertain the symmetry of market sentiments in each of the years for the six currencies considered.
An objective analysis of market sentiments in terms of mere diagnostic tool seem to be quite challenging; thus making a strong case for alternative methods of analysis proposed in this paper. Towards this, we take recourse to the methods outlined in Sections 5 and 6. For example, the Pearson’s chi square and likelihood ratio test sta-

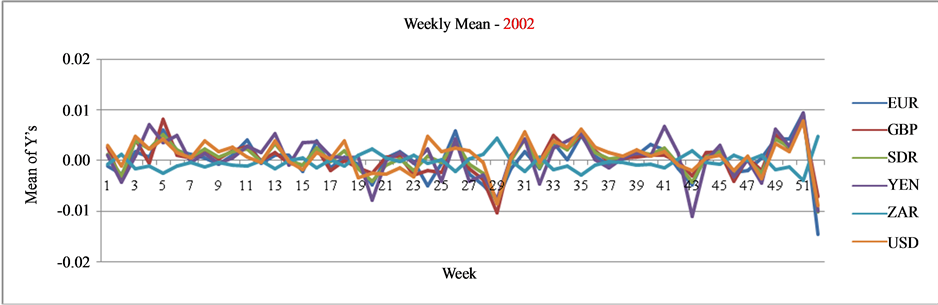


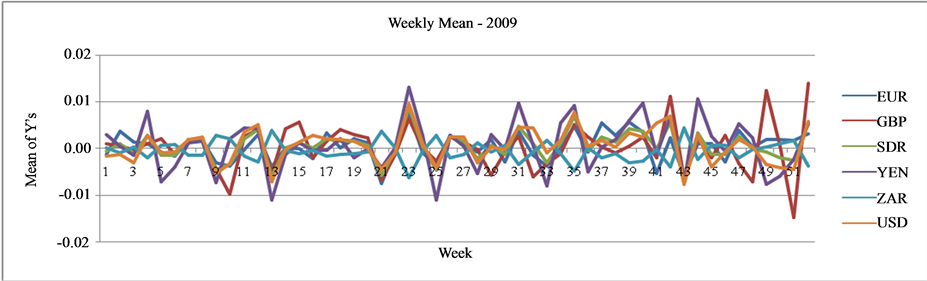
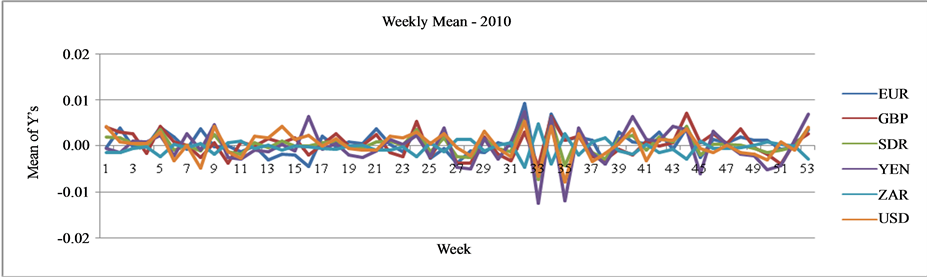
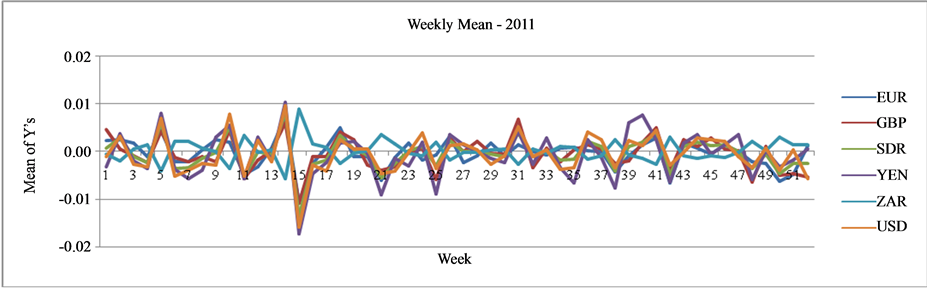
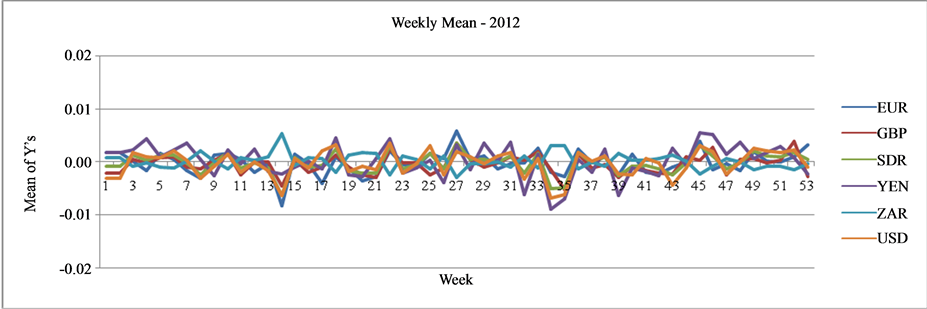
Figure 1. Graph of weekly average of log returns of major currencies during 2001-2012.
tistics for testing 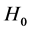 versus
versus  using the formula (15) and (16) are calculated for the six currencies across the 12 years. These are reported in Table3 It is seen that four
using the formula (15) and (16) are calculated for the six currencies across the 12 years. These are reported in Table3 It is seen that four  values are not reported in the table as the observed weekly frequency turned out to be zero; rendering the computation of
values are not reported in the table as the observed weekly frequency turned out to be zero; rendering the computation of 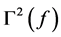 untenable. From the
untenable. From the
table of chi square distribution, at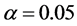 , we have
, we have . The computed test statistics values which are significant at 5% level of significance are highlighted in bold font. It is seen that the drift in market sentiments across the major currencies over the years reveal different pictures. Based on the significant values reported in Table 3, the years under consideration can be grouped into two regimes, the first regime consisting of the years 2005, 2007, 2008, 2009, 2010, 2011, 2012and the second consisting of the years 2001, 2002, 2003, 2004, 2006. It is interesting to point out that in the first regime, except for one currency each (YEN, EUR, GBP, USD, ZAR, EUR and ZAR in that order), market sentiments of the currencies were symmetric. Moreover SDR
. The computed test statistics values which are significant at 5% level of significance are highlighted in bold font. It is seen that the drift in market sentiments across the major currencies over the years reveal different pictures. Based on the significant values reported in Table 3, the years under consideration can be grouped into two regimes, the first regime consisting of the years 2005, 2007, 2008, 2009, 2010, 2011, 2012and the second consisting of the years 2001, 2002, 2003, 2004, 2006. It is interesting to point out that in the first regime, except for one currency each (YEN, EUR, GBP, USD, ZAR, EUR and ZAR in that order), market sentiments of the currencies were symmetric. Moreover SDR

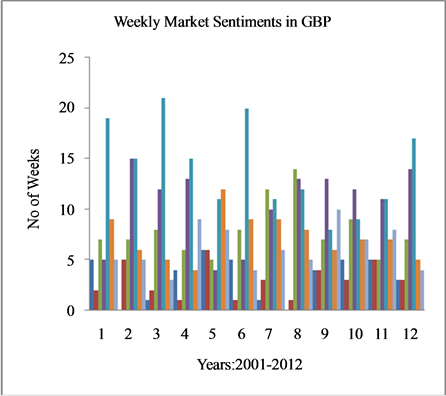



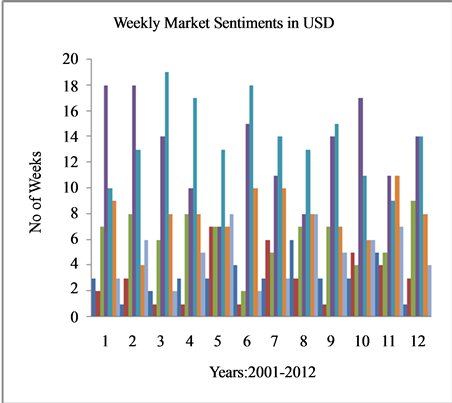
Figure 2. Weekly Market Sentiments in six major currencies during the years 2001-2012.
currency exhibited symmetric market sentiments during all the years of regime 1. It is worthwhile to recognize that most of the years in regime 1 consisted of post global economic downturn periods triggered during the mid
Table 3. Computed value of chi square and likelihood ratio test statistics.
dle of the year 2008. The year 2011 also witnessed the economic crisis in Greece. This event may partly explain the existence of continued symmetric market sentiment behaviour witnessed by all the currencies in the year 2012; except ZAR. These geo-political factors coupled with economic recession possibly could have dampened the exchange rate market activity causing aforementioned symmetry of market sentiments captured by the goodness of fit tests proposed here. Turning to the second regime, in the year 2001, except for YEN and USD, the market sentiments in other currencies were highly speculative, while in 2002, three currencies namely, EUR,GBP and ZARexhibited significant speculative trends. In each of the remaining years 2003, 2004 and 2006, four currencies showed significant speculative trends in market sentiments of which, GBP, SDR and USD currencies were common. In general, across the entire study period 2001-2012, non-symmetric market sentiments were witnessed during six years for the currency EUR, and five years for the currency GBP, while it was least in the case of the currency YEN. The currencies SDR, ZAR and USD witnessed equal number of years of nonsymmetric sentiments, if not necessarily in the same years. It may be concluded that that no single economic event can be attributed for the significance drift in market sentiments; but it appears to be a combination of a multitude of factors including geo-political, social and global and regional events.
Table 4 provides the measure 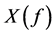 given by equation (18) for ascertaining the direction of market sentiments whenever they are statistically significant. The absence of an entry indicates that corresponding to the pair of currency and year, market sentiments follow symmetric multinomial model discussed earlier. It is interesting to note that in both regimes, market sentiments showed a tendency of buoyancy since
given by equation (18) for ascertaining the direction of market sentiments whenever they are statistically significant. The absence of an entry indicates that corresponding to the pair of currency and year, market sentiments follow symmetric multinomial model discussed earlier. It is interesting to note that in both regimes, market sentiments showed a tendency of buoyancy since 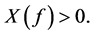 In other words, across the currencies and years as indicated in Table 4, smiling sentiment were witnessed in the FOREX trading.
In other words, across the currencies and years as indicated in Table 4, smiling sentiment were witnessed in the FOREX trading.
Table 5 provides the maximum likelihood estimates of probabilities of weekly market sentiments across the six currencies and for the years 2001-2012, using the formula (7) discussed in Section (3). Using these probabilities one can write down the fitted multinomial probability model for each of the currencies over the years 2001-2012, using the Equation (6) of Section3. As an illustration, for the currency EUR and the year 2001, the multinomial model with seven market sentiment states is given by

Similarly for the currency USD and the year 2012, the multinomial model is given by

Table 4. X(f)—measure of drift in market sentiments.
and so on.
The significance of these probability estimates in Table 5 can be discussed in terms of criteria developed in Section 6 earlier. We observe that, since 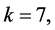 we have
we have . Using the Definition (1), we observe that, viewed across the currencies and the years1) Very few states are weekly persistent since
. Using the Definition (1), we observe that, viewed across the currencies and the years1) Very few states are weekly persistent since
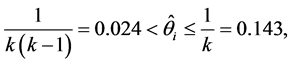
for many states. This implies that the chance that market sentiment remains in a typical state is at least equal to 0.024, in other words market sentiment states tend to move over the different states with a frequency of at least one week to 7 weeks out of 52 trading weeks in a year in the long run.
2) The calm sentiment 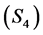 and the incline sentiment
and the incline sentiment 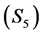 seem to be the moderately persistent across the six currencies and the years considered with a very few exceptions in some of the currencies and the years. The implication of this statement is that in a 52-week trading year, a weekly trading seller seems to have gained in at least 7 trading weeks. All the probability estimates of moderately persistent states are indicated in the bold font in Table5
seem to be the moderately persistent across the six currencies and the years considered with a very few exceptions in some of the currencies and the years. The implication of this statement is that in a 52-week trading year, a weekly trading seller seems to have gained in at least 7 trading weeks. All the probability estimates of moderately persistent states are indicated in the bold font in Table5
3) None of the market sentiment states are strongly persistent, since  This implies that a seller can neither hope to gain nor lose if he or she decides to persist with a fixed weekly investment strategy throughout the year.
This implies that a seller can neither hope to gain nor lose if he or she decides to persist with a fixed weekly investment strategy throughout the year.
The application of Definition (2) helps to identify clusters of similar market sentiment states in terms of their persistency. For example, for the currency EUR and the year 2001, we observe that  is the class of weekly persistent states and
is the class of weekly persistent states and 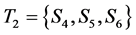 is the class of moderately persistent states. Thus for the class
is the class of moderately persistent states. Thus for the class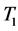 ,
,  ,
, 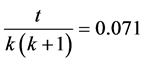
 ,
, 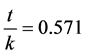 , and
, and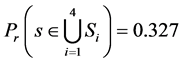 . Also for the class
. Also for the class![]() ,
,  ,
, 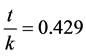
 ,
, 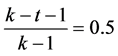 , and
, and . Thus following Definition (2), it is seen that the cluster of states
. Thus following Definition (2), it is seen that the cluster of states 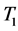 is weakly persistent while the cluster of states
is weakly persistent while the cluster of states 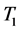 is strongly persistent. One may proceed to identify the clusters of similar market sentiment states for other currencies and the different years. The details are omitted.
is strongly persistent. One may proceed to identify the clusters of similar market sentiment states for other currencies and the different years. The details are omitted.
The approach of analyzing exchange rate time series data can be extended to study monthly or quarterly market sentiments. In the latter case, we make appropriate modification by using the monthly means and standard deviations as given by Equations (11) and (12) in the classification rule (3). The findings of the analysis of the monthly market sentiments for the six currencies and for the years 2001 to 2012 are not reported in this paper but an interested reader can access these findings from the first author.
8. Discussion and Conclusions
FOREX plays a significant role in global economy stimulation. The exchange rates tend to fluctuate from time
to time with FOREX being a commodity. Besides other factors, government policies have a compelling influence on the fundamental FOREX market analysis. Evaluating the international currency exchange rates helps the trader develop a well-informed and strong trading strategy. Perception of volatility in exchange rates is a strong tool in this evaluation. Volatility is observed in daily, weekly, monthly or yearly archives of exchange rates. Any investment decision based on the daily movement of exchange rates is highly speculative. But decisions based on the analysis of weekly, monthly or quarterly movements may seem less speculative since this forms a pattern which is evident. But its understanding is not easy for a trader. To circumvent this, we advocate the analysis of exchange rates based on the concept of market sentiments; which is very user-friendly and easily understood by a trader. The focus of the study in this paper, therefore, has been to analyse weekly and monthly exchange rates and to have a better understanding of the movement in exchange rates in terms of market sentiments.
In this paper, a method is proposed whereby, volatility in exchange rates is translated into market sentiments based on simple data driven classification rules. A suitable probability model is proposed for the outcomes of the classification rules. The classification rules demarcate the fluctuations visible in any financial data. The sentiment states define these appropriately and a multinomial probability model has been proposed to capture the uncertainties in the movement of market sentiments. Two nonparametric tests are proposed to test the hypothesis of symmetric market sentiments. Two indices are suggested to measure the drift in market sentiments. A signed measure which indicates the smiling or frowning state of sentiment is proposed when the market sentiment model is asymmetric. Some criteria which ascertain the significance of individual market sentiments or a cluster of similar sentiments are given. The methodology developed in this paper has been applied to weekly exchange rates of Botswana Pula against six currencies. The summary findings of the analysis are as follows:
1) The weekly and monthly exchange rate market sentiments more or less appear to fall into two regimes of symmetric and asymmetric sentiments.
2) All the six currencies exhibited smiling sentiments given the scenario of asymmetric market sentiments.
3) All the currencies have clusters of sentiment states which are strongly persistent indicating that exchange rate trading across the currencies and the years are buoyant.
4) The computations involved in the proposed technique can be done easily in MS Excel or any other compatible software unlike as in the case of sophisticated volatility estimation procedures, such as GARCH, which require econometrics software. The latter limits its application from the point of view of a street trader.
The market sentiment analysis techniques advocated here is not limited to exchange rates alone but could be used to analyze any financial and economic time series data such as stock and share prices, interest rates of bonds and securities and so on. It would be interesting to apply these techniques to NYSE, NASDAQ, TSE, LSE, etc. to understand the market sentiments in these global stock exchanges and render meaningful comparisons. For example, a political economist would be interested to compare the market sentiment of a country’s premier stock exchange that prevailed during two governments formed by opposite political parties. Besides analyzing market sentiments on a micro scale such as weekly or monthly, one may also adopt the same technique to a macro scale analysis, for example, yearly market sentiments given a large time series data.
[1] REFERENCES
[2] J. C. Hull, “Options, Futures, and Other Derivatives,” 5th Edition, Englewood Cliffs, Prentice Hall, 2003.
[3] R. F. Engel, “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation,” Econometrica, Vol. 50, No. 4, 1982, pp. 987-1008. http://dx.doi.org/10.2307/1912773
[4] T. A. Bollerslev, “A Conditional Heteroscedastic Time Series Model for Speculative Prices and Rates of Return,” Review of Economics and Statistics, Vol. 69, No. 3, 1987, pp. 542-547. http://dx.doi.org/10.2307/1925546
[5] D. Blake, “Financial Market Analysis,” 2nd Edition, John Wiley & Sons Ltd., Chichester, 2005.
[6] N. Sheldon, “Option Volatility & Pricing: Advanced Trading Strategies and Techniques,” McGraw Hill Professional, New York, 1994.
[7] K. Chung and O. Jorda, “Fluctuations in Exchange Rates and the Carry Trade,” Working Paper No. 405, Institute for Monetary and Economic Research, The Bank of Korea, Seoul, 2009.
[8] A. Markiewicz, “Model Uncertainty and Exchange Rate Volatility,” International Economic Review, Vol. 53, No. 3, 2012, pp. 815-844. http://dx.doi.org/10.1111/j.1468-2354.2012.00702.x
[9] C. F. Baum and N. Ozkan, “Nonlinear Effects of Exchange Rate Volatility on the Volume of Bilateral Exports,” Journal of Applied Econometrics, Vol. 19, No. 1, 2004, pp. 1-23. http://dx.doi.org/10.1002/jae.725
[10] T. G. Andersen, T. Bollerslev, F. Diebold and P. Labys, “The Distribution of Realized Exchange Rate Volatility,” Journal of the American Statistical Association, Vol. 96, No. 453, 2000, pp. 42-55. http://dx.doi.org/10.1198/016214501750332965
[11] C. Christiansen, “Intertemporal Risk-Return Trade-Off in Foreign Exchange Rates,” Journal of International Financial Markets, Institutions & Money, Vol. 21, No. 4, 2011, pp. 535-549. http://dx.doi.org/10.1016/j.intfin.2011.02.001
[12] O. de Bandt, “Measuring Long-Run Exchange Rate Pass-Through-Recent Developments in International Money and Finance,” Economics, Vol. 2, 2008, pp. 1-36.
[13] J. J. Lim and C. S. Yue, “Political Risk and the Exchange Rate: An Exploration with a Regime Switching Model, Edited Volumes—Information Technology in Asia: New Development Paradigms,” Institute of Southeast Asian Studies, Singapore City, 2002.
[14] I. Nouri, “Exchange Rate Forecasting: A Combination Approach,” American Journal of Scientific Research, No. 22, 2011, pp. 110-118.
[15] R. Ramasamy and M. H. M. Helmi, “Impact of Weiner Process on Exchange Rate Forecasting,” Global Journal of Management and Business Research, Vol. 10, No. 3, 2010, pp. 69-78.
[16] S. M. Ross, “An Elementary Introduction to Mathematical Finance: Options and Other Topics,” Cambridge University Press, Cambridge, 2003.
[17] E. L. Grant and R. S. Leavenworth, “Statistical Quality Control,” McGraw-Hill, New York, 2005.
[18] A. Stuart and K. Ord, “Kendall’s Advanced Theory of Statistics, Volume1: Distribution Theory,” 6th Edition, Holder Arnold, London, 1994.
[19] A. Stuart, K. Ord and S. Arnold, “Kendall’s Advanced Theory of Statistics, Volume 2 A: Classical Inference & the Linear Model,” 6th Edition, Holder Arnold, London, 1999.
NOTES

*Corresponding author.


