Open Journal of Statistics
Vol. 3 No. 1 (2013) , Article ID: 28068 , 5 pages DOI:10.4236/ojs.2013.31006
Strong Law of Large Numbers for a 2-Dimensional Array of Pairwise Negatively Dependent Random Variables
1Department of Mathematics and Computer Science, Chulalongkorn University, Bangkok, Thailand
2Centre of Excellence in Mathematics, CHE, Bangkok, Thailand
Email: nattakarn.c@chula.ac.th
Received October 30, 2012; revised November 30, 2012; accepted December 14, 2012
Keywords: Strong Law of Large Numbers; Negatively Dependent; 2-Dimensional Array of Random Variables
ABSTRACT
In this paper, we obtain the strong law of large numbers for a 2-dimensional array of pairwise negatively dependent random variables which are not required to be identically distributed. We found the sufficient conditions of strong law of large numbers for the difference of random variables which independent and identically distributed conditions are regarded. In this study, we consider the limit as ![]() which is stronger than the limit as
which is stronger than the limit as 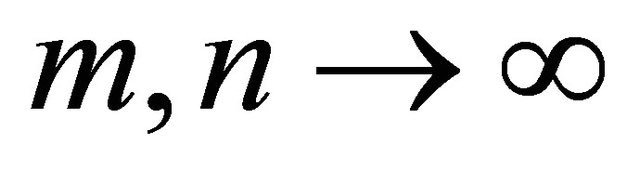 when m, n are natural numbers.
when m, n are natural numbers.
1. Introduction and Main Results
|
as |
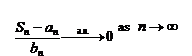 Let
Let  be a sequence of random variables. We say that
be a sequence of random variables. We say that 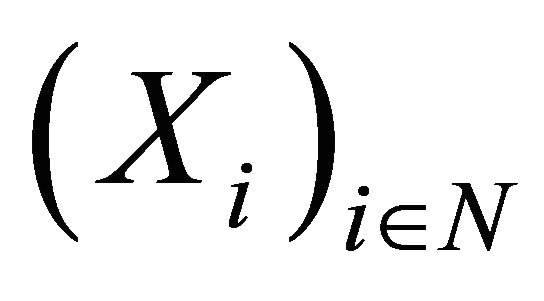 satisfies the strong law of large numbers
satisfies the strong law of large numbers (SLLN) if there exist sequences of real numbers 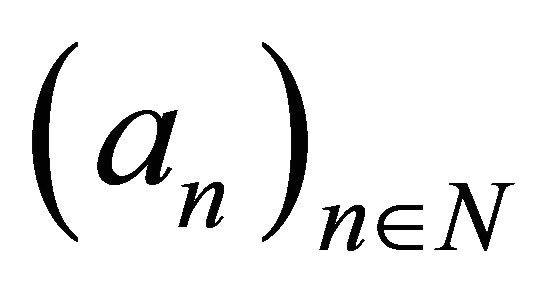
and 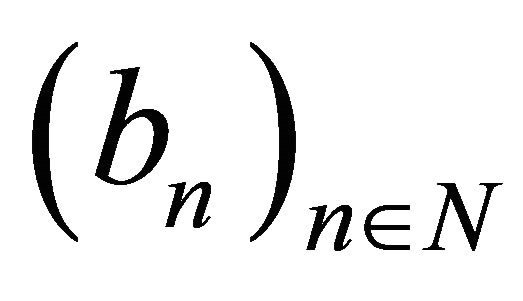 such that
such that 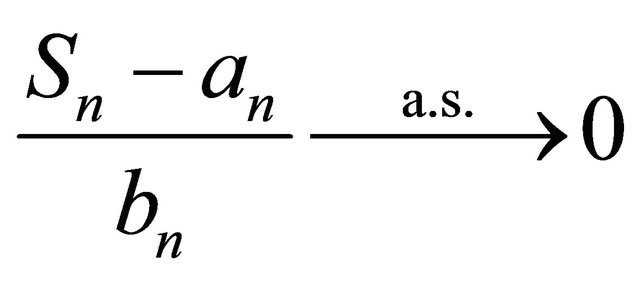 as
as![]() . where
. where 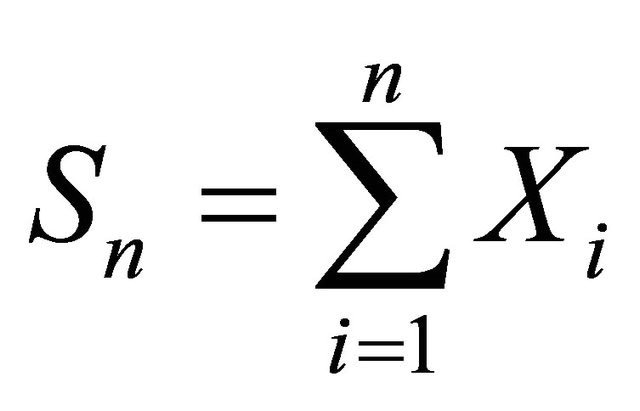 and the abbreviation a.s. stands for almost surely.
and the abbreviation a.s. stands for almost surely.
To study the strong law of large numbers, there is a simple question come in mind. When does the sequence 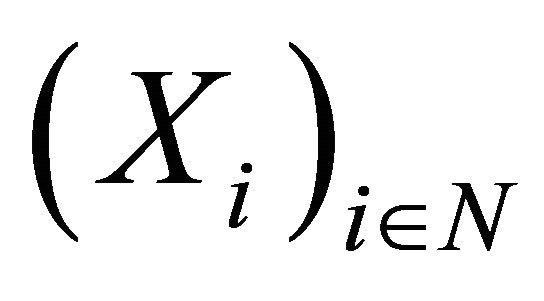 satisfy the SLLN? Many conditions of the sequence
satisfy the SLLN? Many conditions of the sequence  have been found for this question. The SLLN are investigated extensively in the literature especially to the case of a sequence of independent random variables (see for examples in [1-3]). After concepts of dependence was introduced, it is interesting to study the SLLN with condition of dependence.
have been found for this question. The SLLN are investigated extensively in the literature especially to the case of a sequence of independent random variables (see for examples in [1-3]). After concepts of dependence was introduced, it is interesting to study the SLLN with condition of dependence.
A sequence  of random variables is said to be pairwise positively dependent (pairwise PD) if for any
of random variables is said to be pairwise positively dependent (pairwise PD) if for any 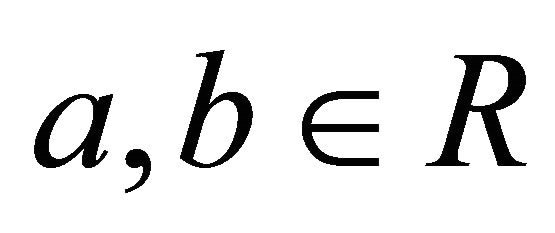 and
and ,
,

and it is said to be pairwise negatively dependent (pairwise ND) if for any  and
and ,
,
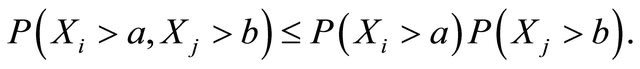
Theorem 1.1-1.5 are examples of SLLN for a sequence of pairwise PD and pairwise ND random variables.
Theorem 1.1. (Birkel, [4]) Let 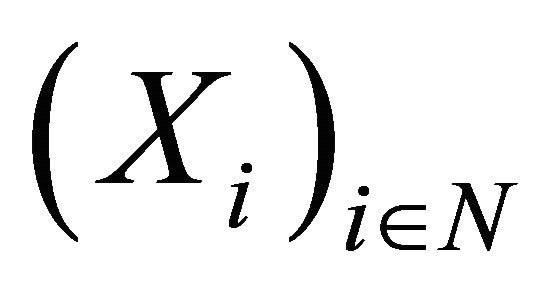 be a sequence of pairwise PD random variables with finite variances. Assume 1)
be a sequence of pairwise PD random variables with finite variances. Assume 1) 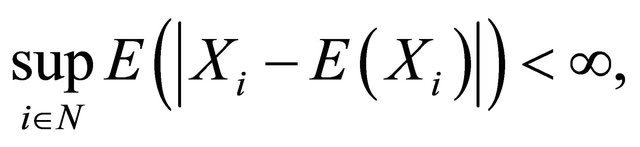
2) 
Then  as
as ![]()
Theorem 1.2. (Azarnoosh, [5]) Let 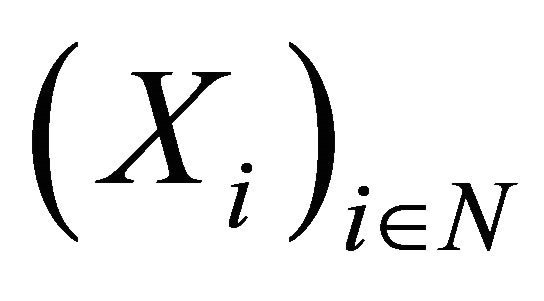 be a sequence of pairwise ND random variables with finite variances. Assume 1)
be a sequence of pairwise ND random variables with finite variances. Assume 1) 
2) 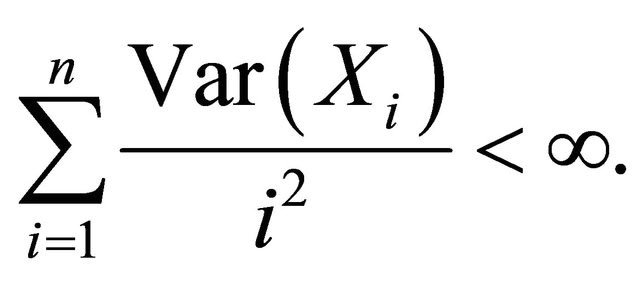
Then 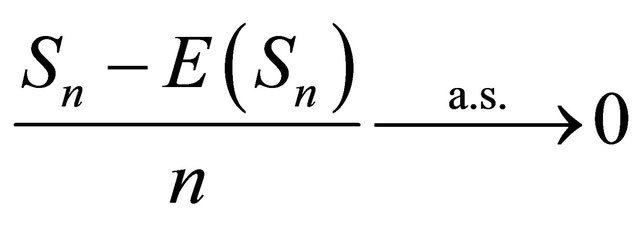 as
as ![]()
Theorem 1.3. (Nili Sani, Azarnoosh and Bozorgnia, [6]) Let 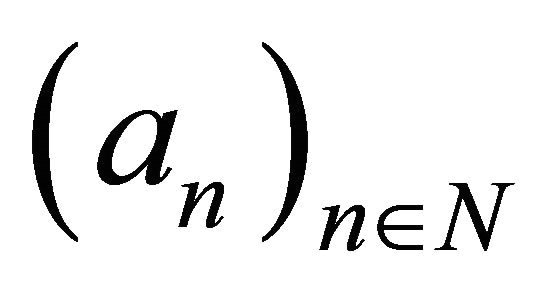 be a positive and increasing sequence such that
be a positive and increasing sequence such that  as
as ![]()
Let 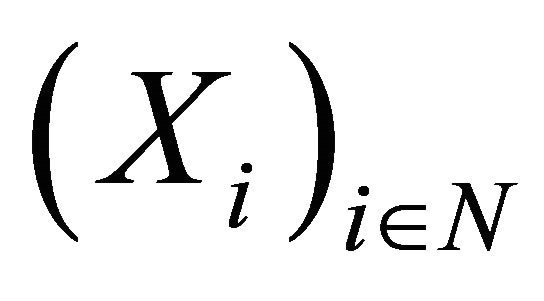 be a sequence of pairwise ND random variables with finite variances such that 1)
be a sequence of pairwise ND random variables with finite variances such that 1) 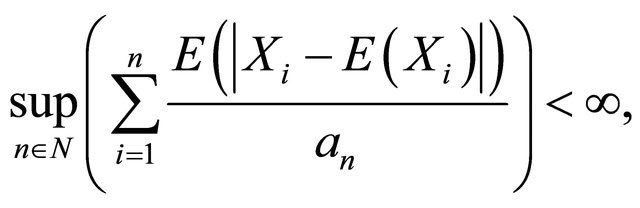
2) 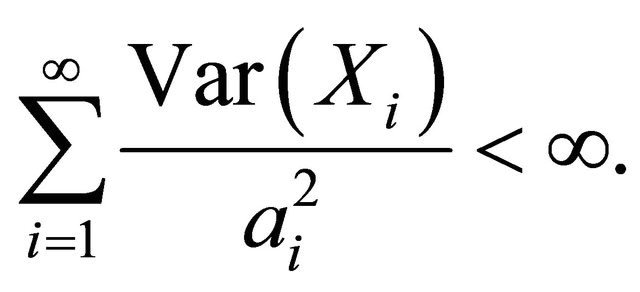
Then 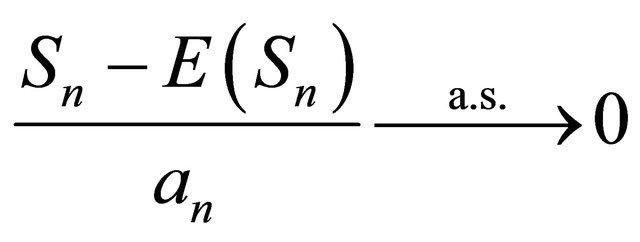 as
as ![]()
In this work, we study the SLLN for a 2-dimensional array of pairwise ND random variables. We say that
 satisfies the SLLN if there exist double sequences of real numbers
satisfies the SLLN if there exist double sequences of real numbers 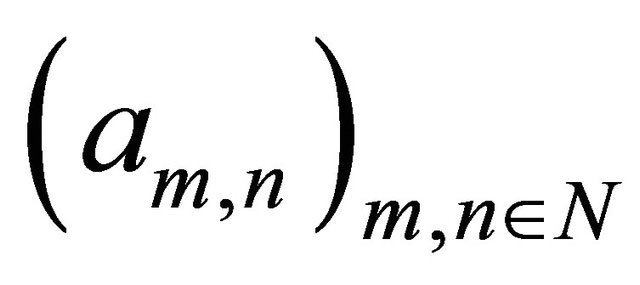 and
and 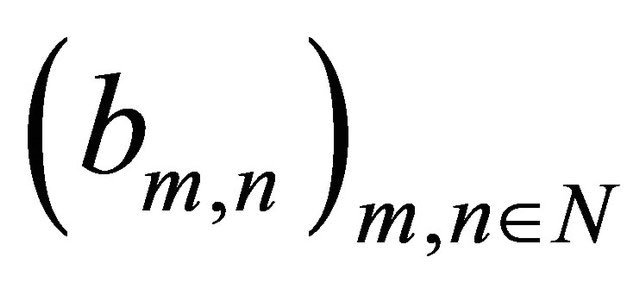 such that
such that 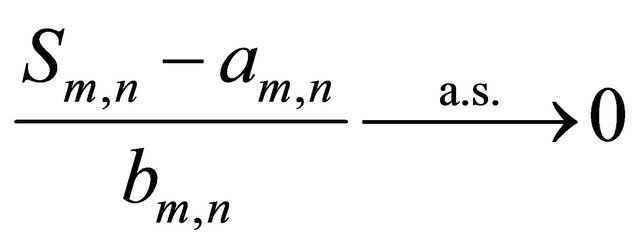 as
as 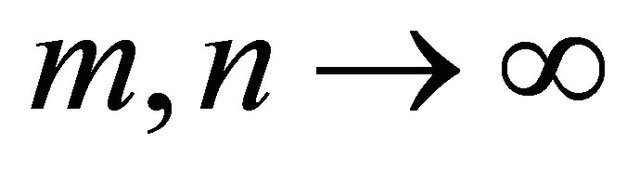 where
where 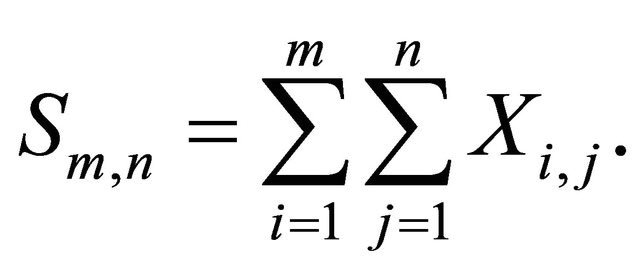
In 1998, Kim, Beak and Seo investigated SLLN for a 2-dimensional array of pairwise PD random variables and it was generalized to a case of weighted sum of 2-dimensional array of pairwise PD random variables by Kim, Baek and Han in one year later. The followings are their results.
A double sequence 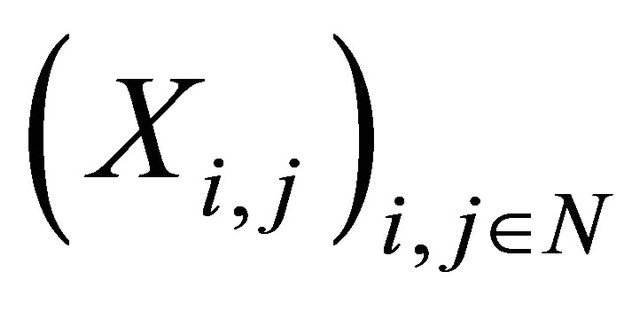 is said to be pairwise positively dependent (pairwise PD) if for any
is said to be pairwise positively dependent (pairwise PD) if for any 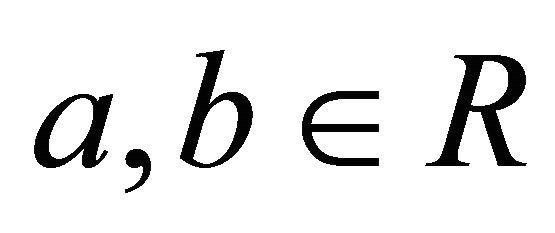 and
and 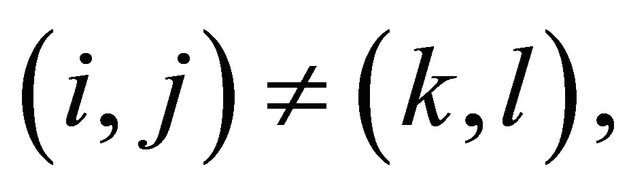
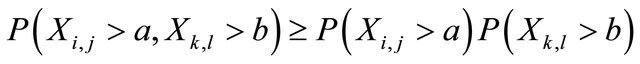
Theorem 1.4. (Kim, Beak and Seo, [7]) Let
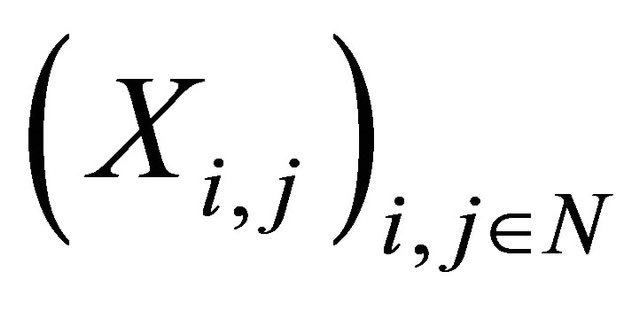 be a 2-dimensional array of pairwise PD random variables with finite variances. Assume 1)
be a 2-dimensional array of pairwise PD random variables with finite variances. Assume 1) 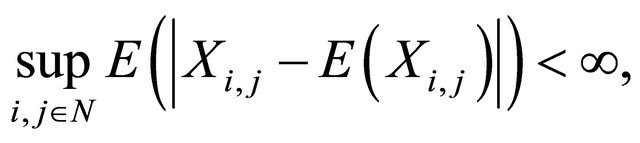
2) 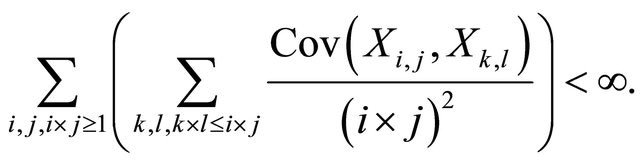
Then 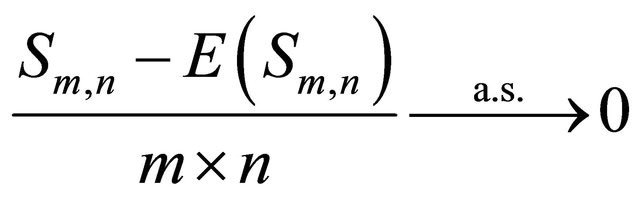 as
as ![]()
Theorem 1.5. (Kim, Baek and Han, [8]) Let  be a 2-dimensional array of positive numbers and
be a 2-dimensional array of positive numbers and 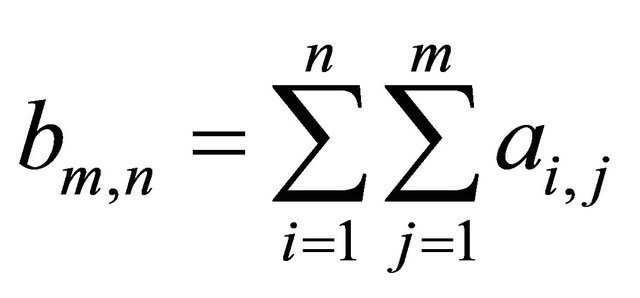 such that
such that  and
and 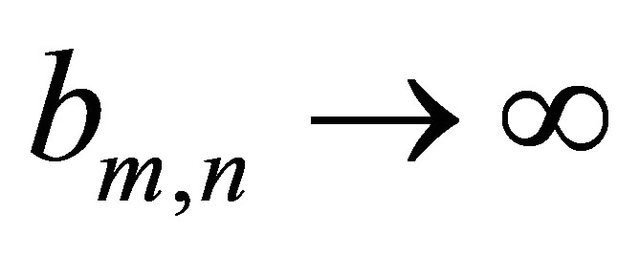 as
as 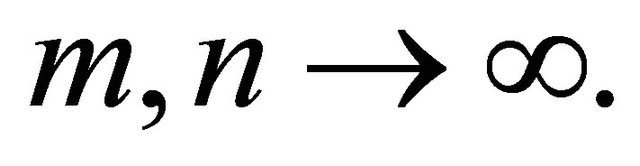
Let  be a 2-dimensional array of pairwise PD random variables with finite variances such that 1)
be a 2-dimensional array of pairwise PD random variables with finite variances such that 1) 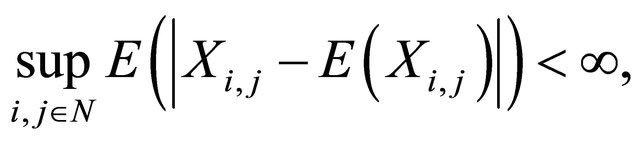
2) 
Then  as
as ![]() where
where 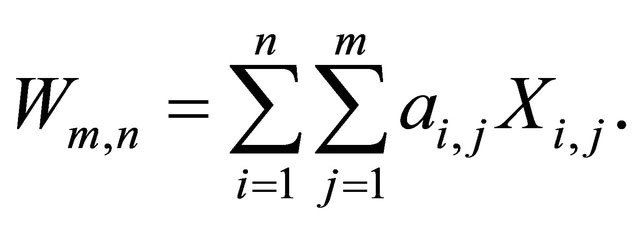
Observe that, for a double indexed sequence of real number 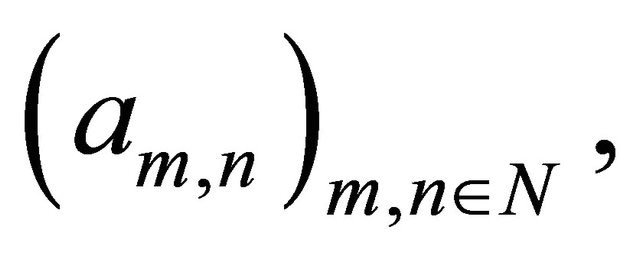 the convergence as
the convergence as ![]() implies the convergence as
implies the convergence as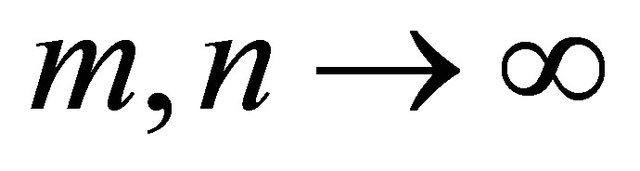 . However, a double sequence
. However, a double sequence 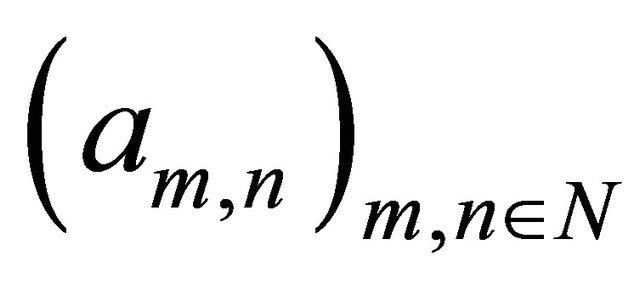 where
where 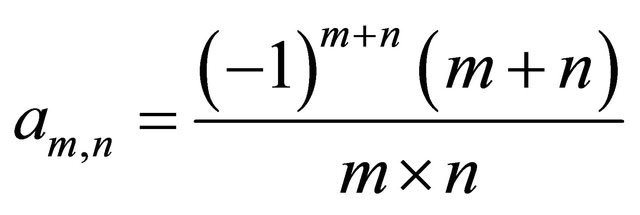 shows us that the converse is not true in general.
shows us that the converse is not true in general.
Our goal is to obtain the SLLN for 2-dimensional array of random variables in case of pairwise ND.
A double sequence 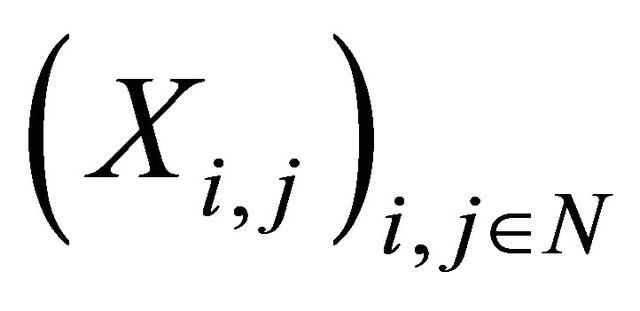 is said to be pairwise negtively dependent (pairwise ND) if for any
is said to be pairwise negtively dependent (pairwise ND) if for any  and
and 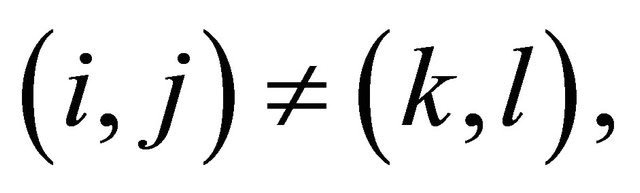

The followings are SLLNs for a 2-dimensional array of pairwise ND random variables which are all our results.
Theorem 1.6. Let 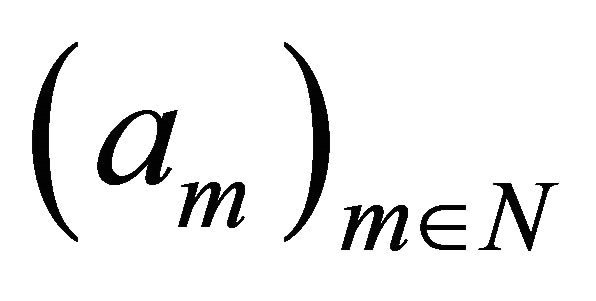 and
and 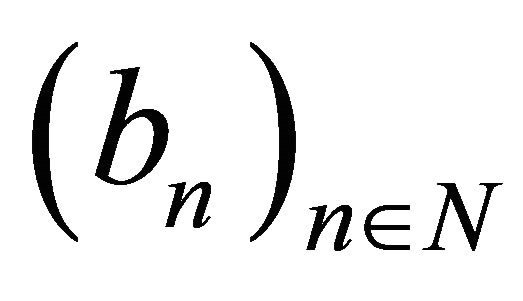 be increasing sequences of positive numbers such that
be increasing sequences of positive numbers such that  which
which  as
as ![]() and
and  as
as ![]()
Let 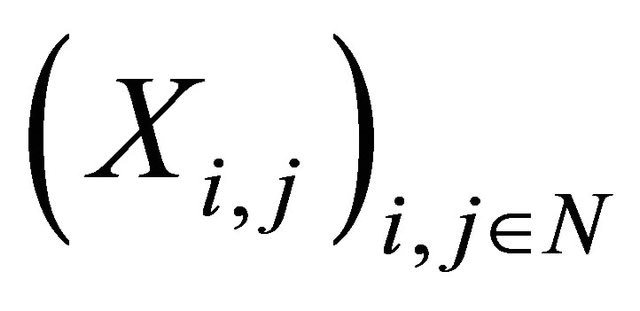 be a 2-dimensional array of pairwise ND random variables with finite variances. If there exist real numbers
be a 2-dimensional array of pairwise ND random variables with finite variances. If there exist real numbers  such that
such that
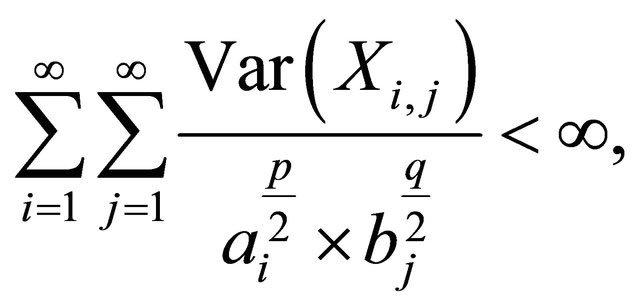
then for any double sequence 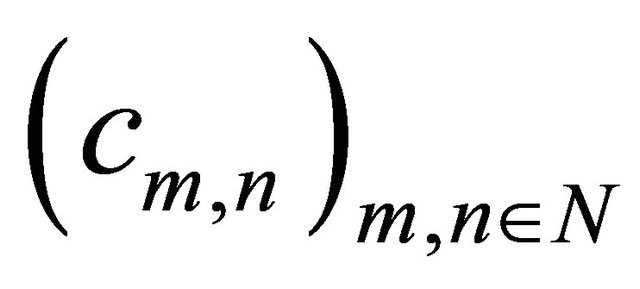 such that
such that
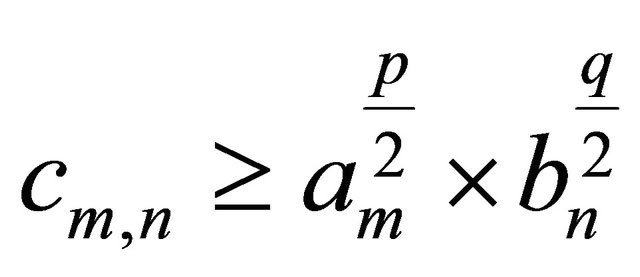 for every
for every 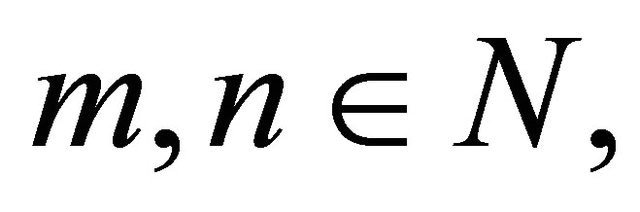
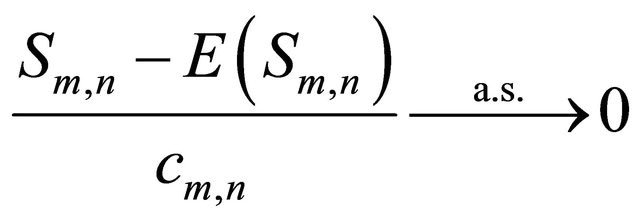 as
as ![]()
The next theorem is the SLLN for the difference of random variables which independent and identically distributed conditions are regarded.
Theorem 1.7. Let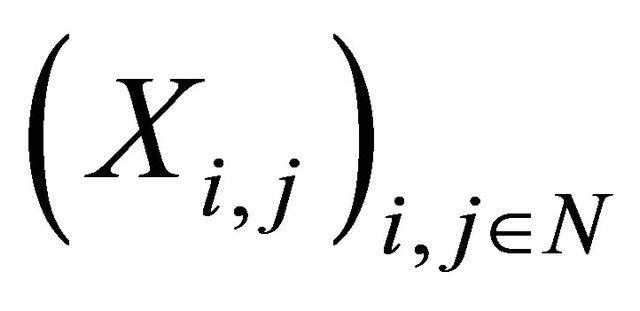 and
and 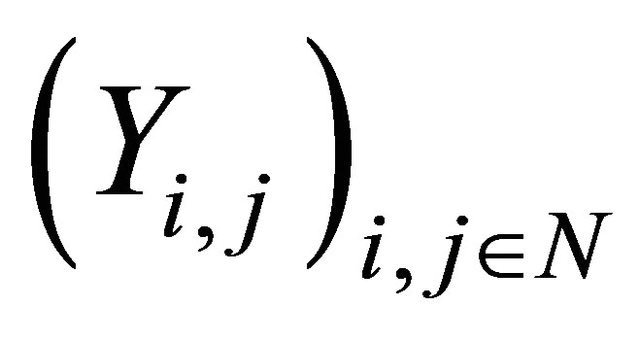 be 2dimensional arrays of random variables on a probability space (Ω, F, P). If
be 2dimensional arrays of random variables on a probability space (Ω, F, P). If

then
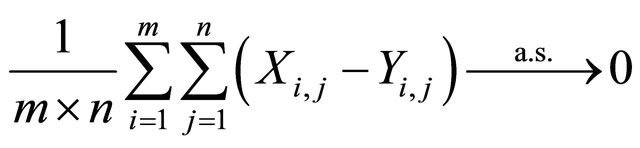
as ![]()
Corollary 1.8 and Corollary 1.9 follow directly from Theorem 1.6 by choosing  and
and 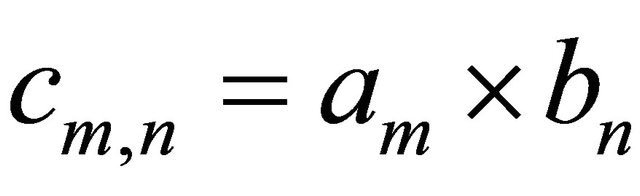 where
where 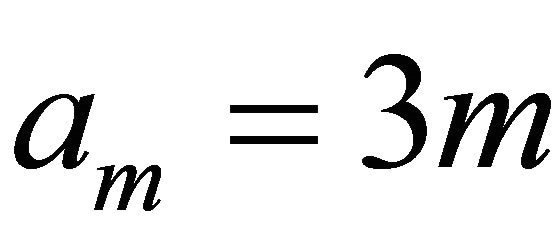 and
and 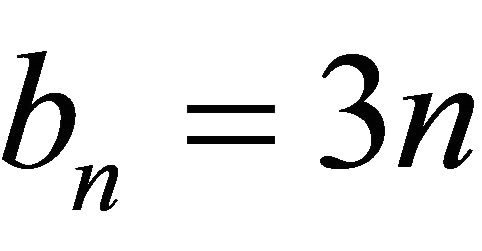 with p = q = 4, respectively.
with p = q = 4, respectively.
Corollary 1.8. Let 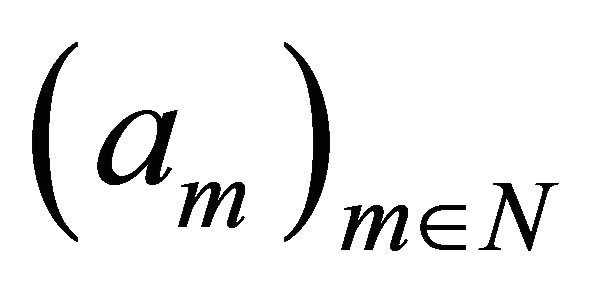 and
and 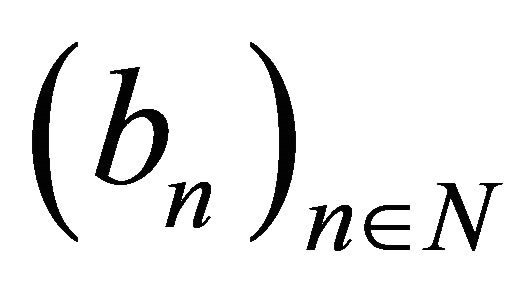 be increasing sequences of positive numbers such that
be increasing sequences of positive numbers such that  which
which 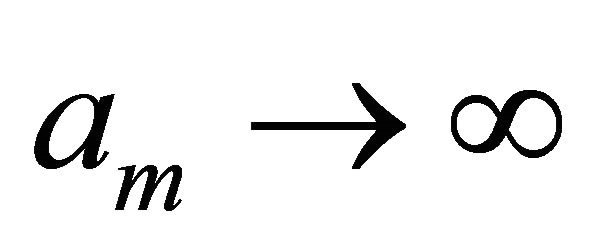 as
as ![]() and
and  as
as ![]()
Let  be a 2-dimensional array of pairwise ND random variables with finite variances. If there exist
be a 2-dimensional array of pairwise ND random variables with finite variances. If there exist 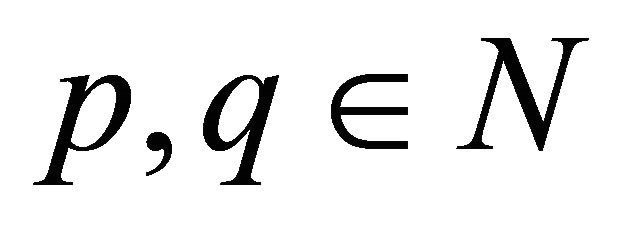 such that
such that
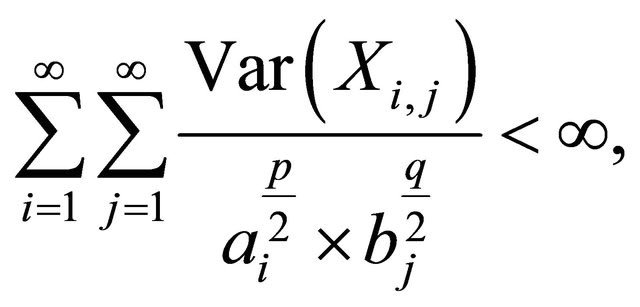
then for any 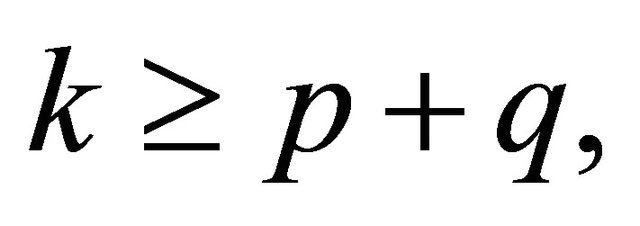
 as
as ![]()
Corollary 1.9. Let  be a 2-dimensional array of pairwise ND random variables with finite variances. If
be a 2-dimensional array of pairwise ND random variables with finite variances. If
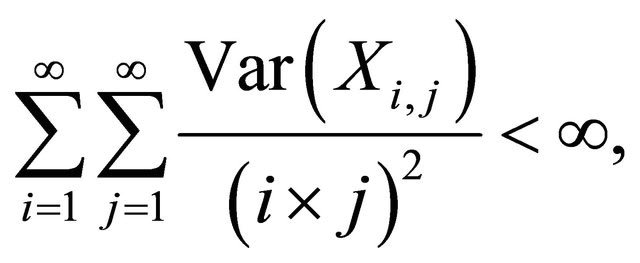
then
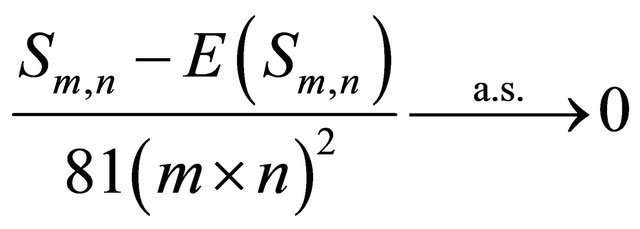 as
as ![]()
2. Auxiliary Results
In this section, we present some materials which will be used in obtaining the SLLN’s in the next section.
Proposition 2.1. (Móricz, [9]) Let 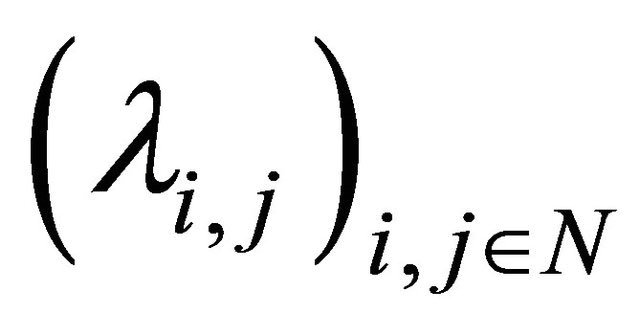 be a double sequence of positive numbers such that for all
be a double sequence of positive numbers such that for all 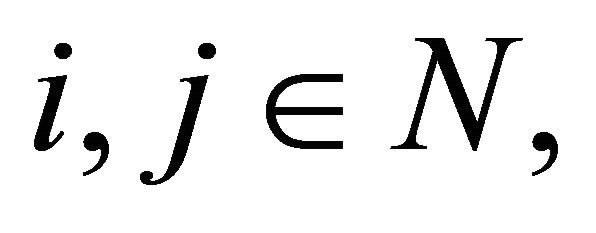
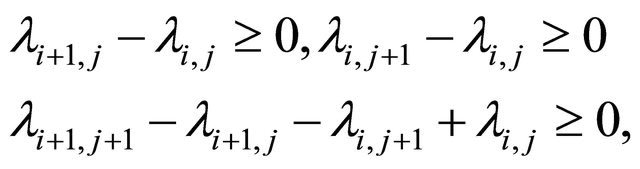
and 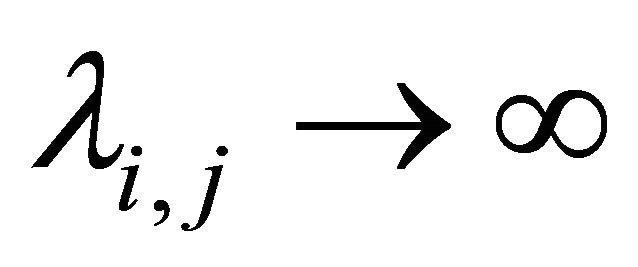 as
as 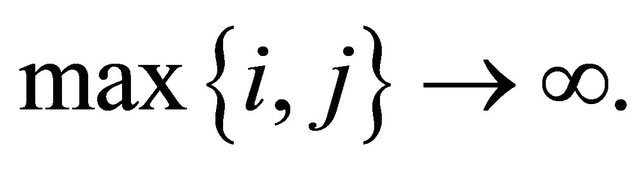
Let 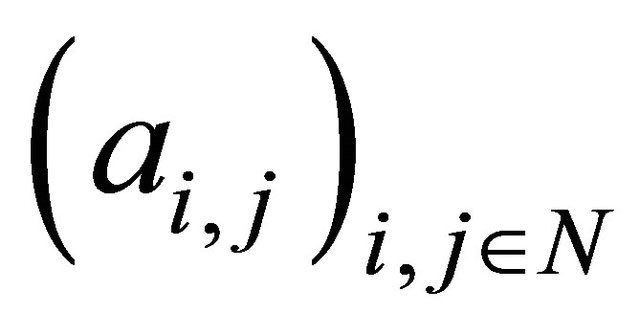 be a double sequence of real numbers. Assume that 1)
be a double sequence of real numbers. Assume that 1) 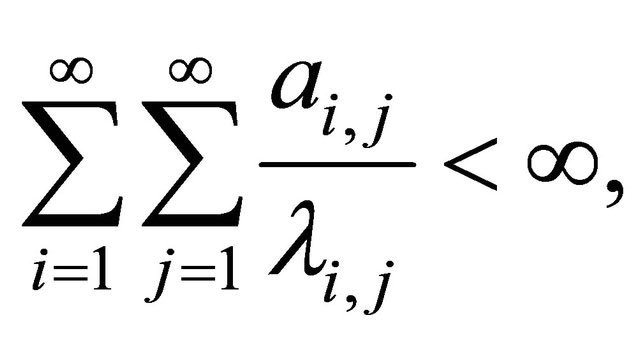
2) 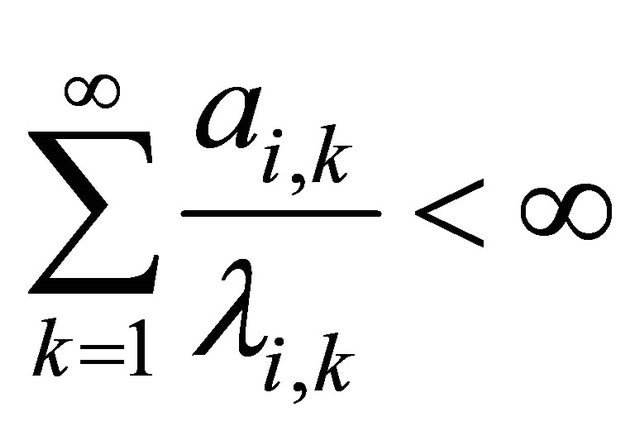 for every
for every  and
and 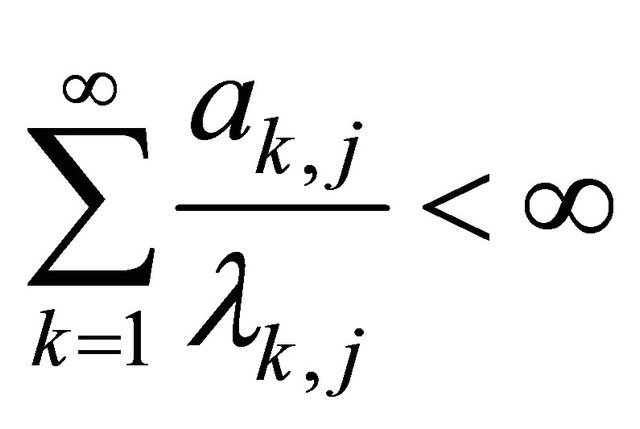 for every
for every 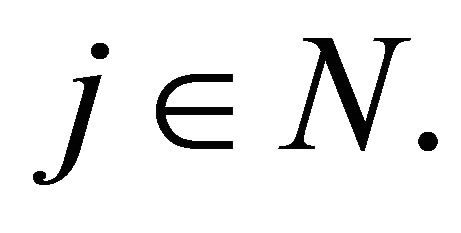 Then
Then 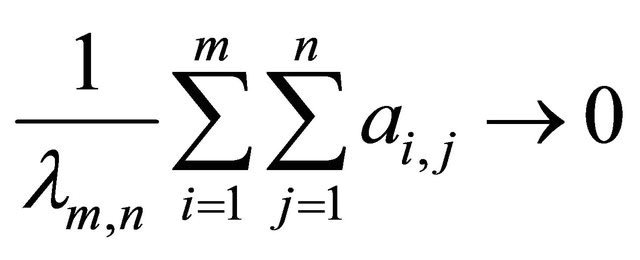 as
as 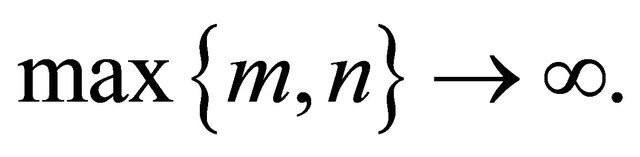
The following proposition is a Borel-Cantelli lemma for a sequence of double indexed events Proposition 2.2. Let 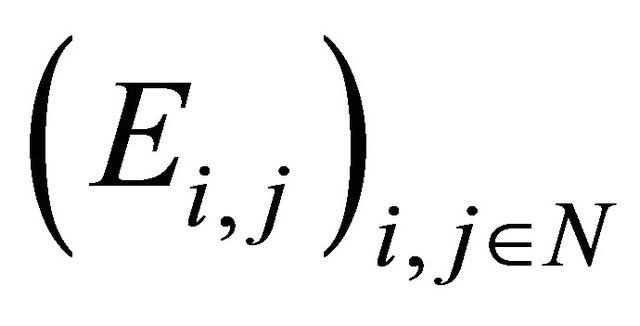 be a double sequence of events on a probability space
be a double sequence of events on a probability space 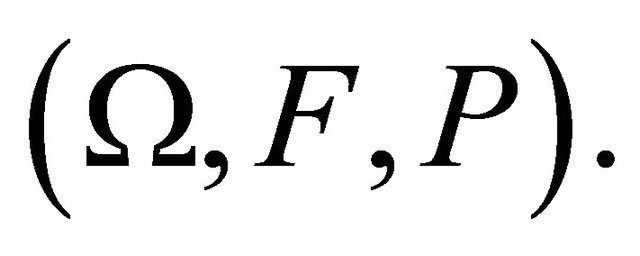 Then
Then

where 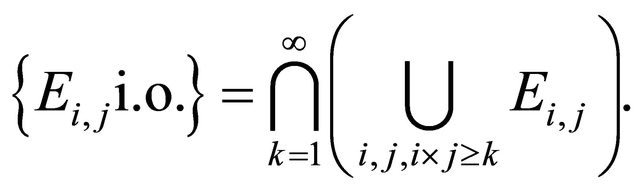
Proof. Let  be such that
be such that 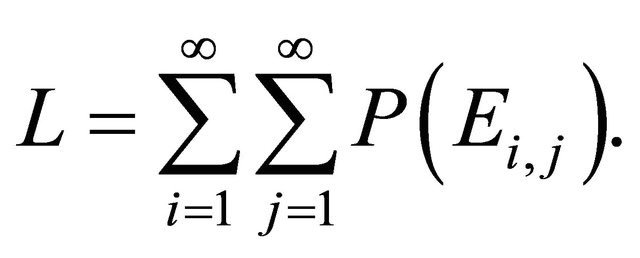 First note that
First note that
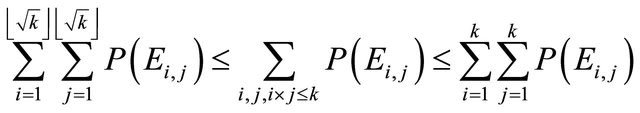
where 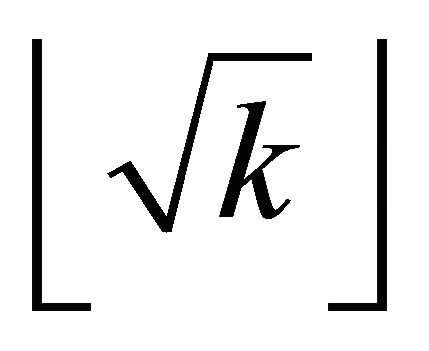 denote the greatest integer smaller than or equal
denote the greatest integer smaller than or equal 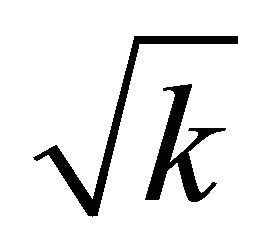 and hence
and hence
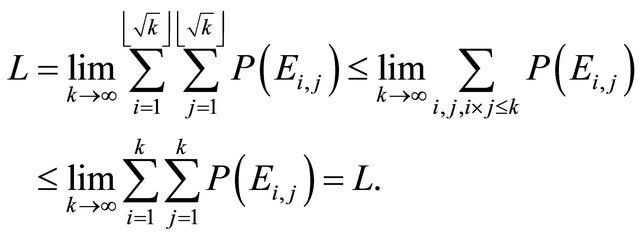
Therefore 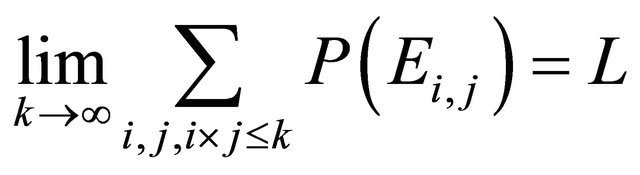 and
and

This completes the proof. □
3. Proof of Main Results
Proof of Theorem 1.6
Let  and define
and define 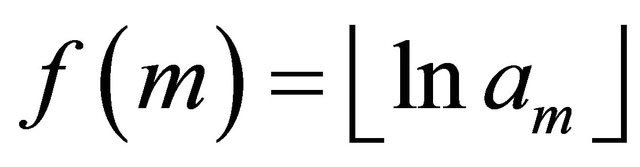 and
and 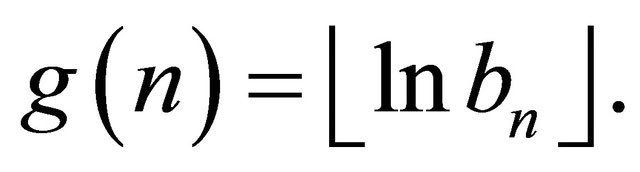
Clearly, f and g are increasing whose facts
 and
and  which imply that
which imply that 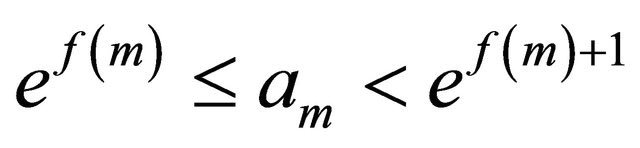 and
and
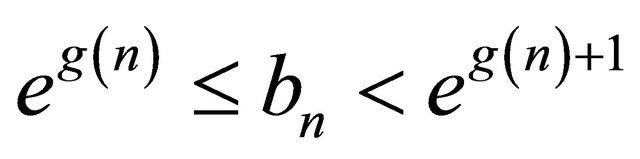 .
.
Let 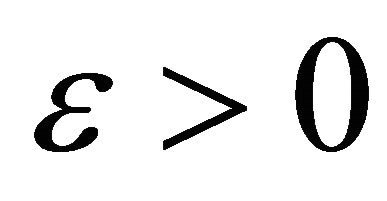 be given. By using the fact that
be given. By using the fact that 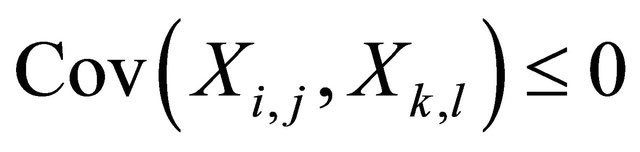 for
for 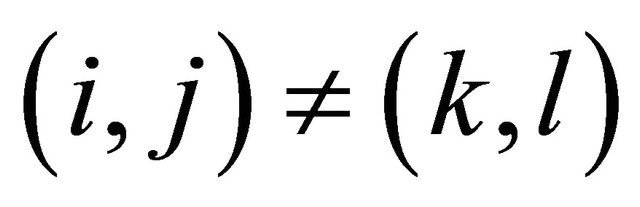 ([10], p. 313), we have
([10], p. 313), we have

From this fact and Chebyshev’s inequality, we have

For each 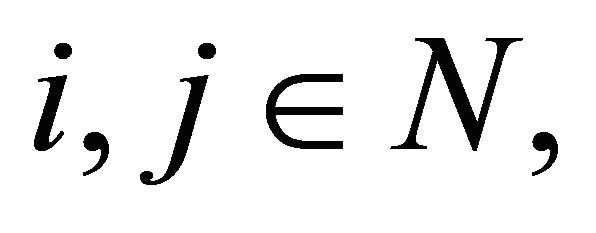 let
let

and 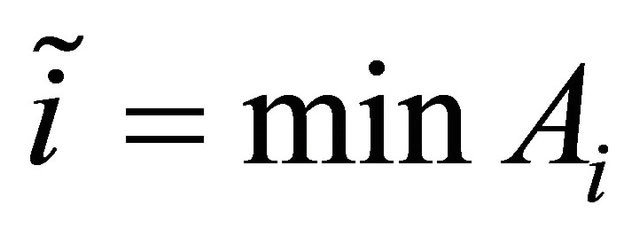 and
and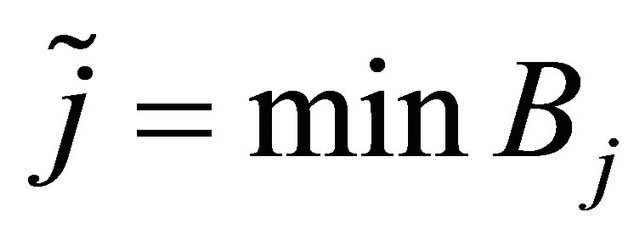 . Since
. Since 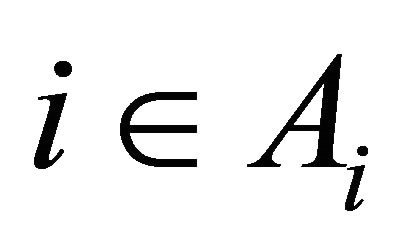 and
and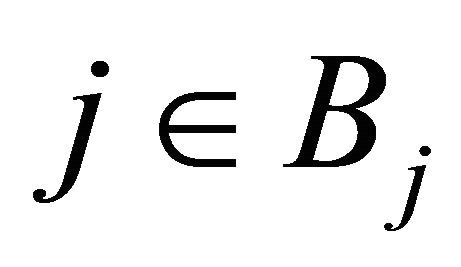 , we have
, we have  and
and . From this facts and (3.1), we have
. From this facts and (3.1), we have

Since 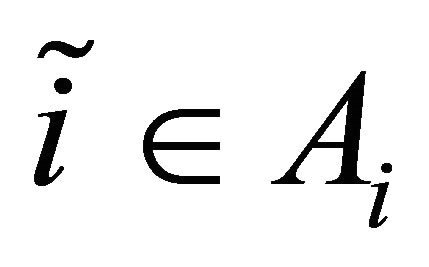 and
and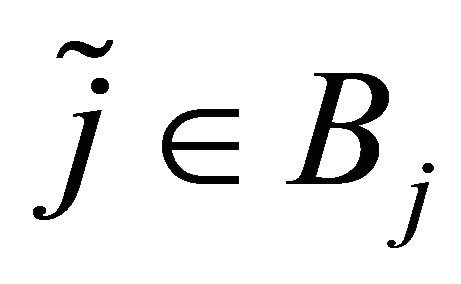 , we have
, we have  and
and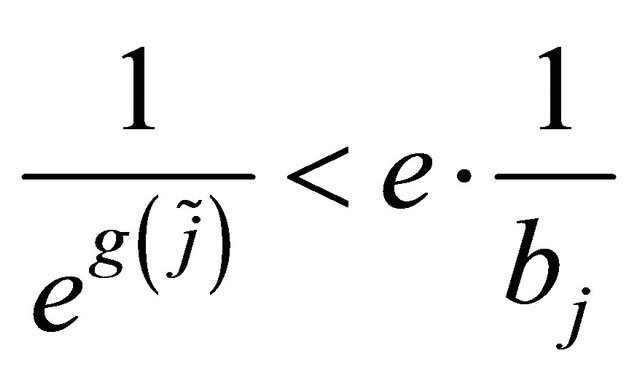 .
.
From this facts and (3.2) together with our assumption 2), we have

By Proposition 2.2 with
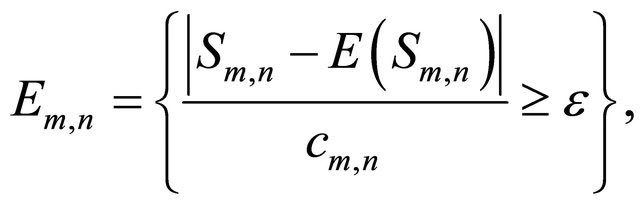
we have  and this hold for every
and this hold for every 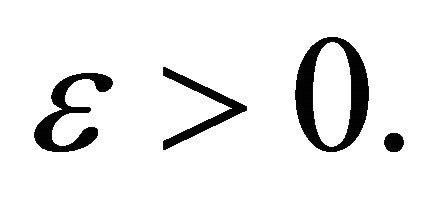 By using the same idea with Theorem 4.2.2 ([11], p. 77), we can prove that
By using the same idea with Theorem 4.2.2 ([11], p. 77), we can prove that
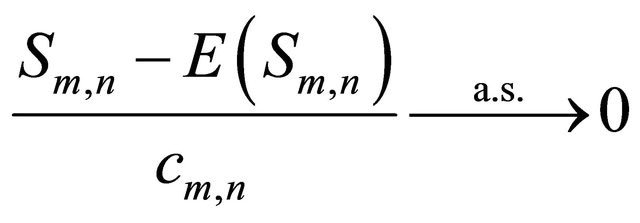 as
as ![]()
Proof of Theorem 1.7
Let 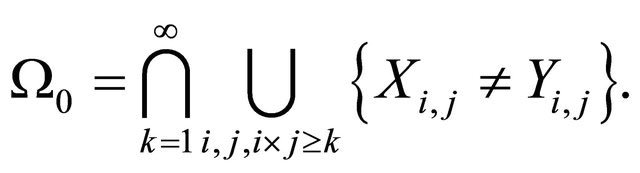 By Proposition 2.2, we have
By Proposition 2.2, we have
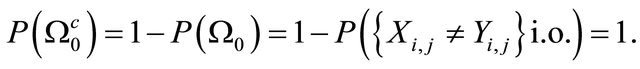
For every 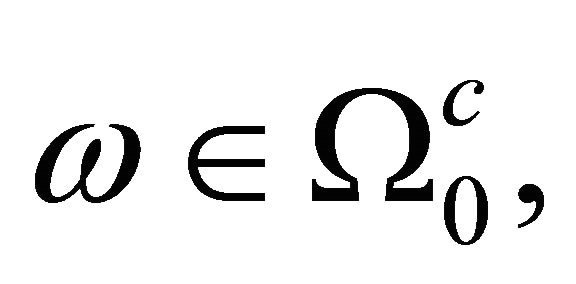 we will show that
we will show that
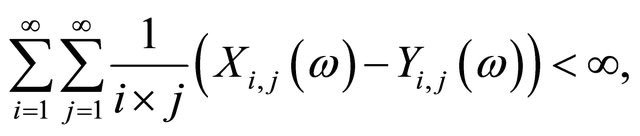 (3.3)
(3.3)
for every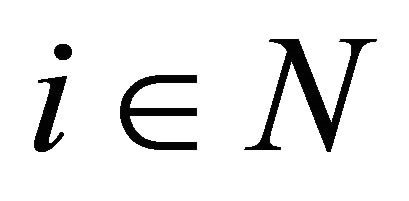 ,
,
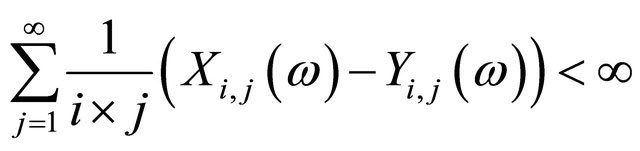 (3.4)
(3.4)
and for every 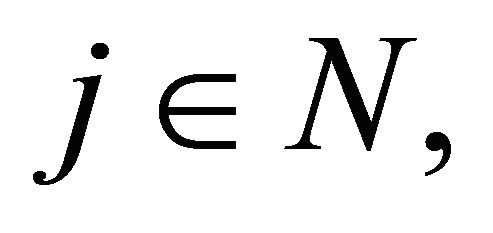
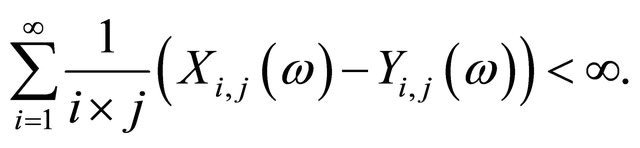 (3.5)
(3.5)
From (3.3), (3.4) and (3.5), we can apply Proposition 2.1 with 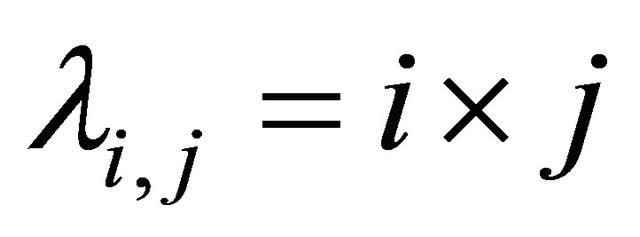 that
that
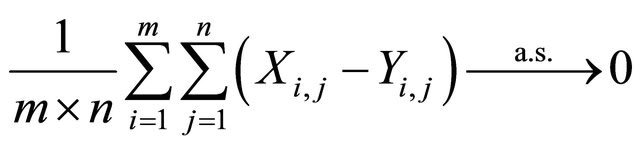
as  We here note that
We here note that 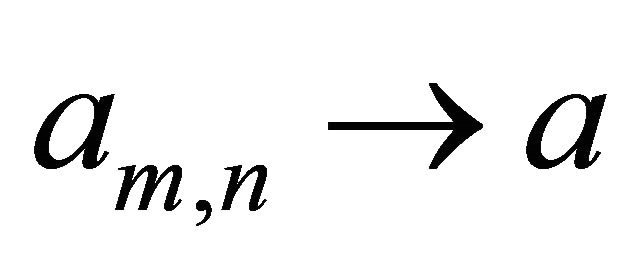 as
as  implies
implies  as
as![]() . Hence
. Hence
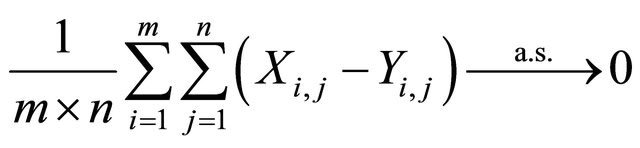
as ![]()
To prove (3.3), (3.4) and (3.5), let  Then there exists
Then there exists 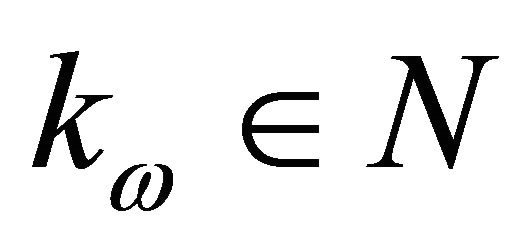 such that for
such that for 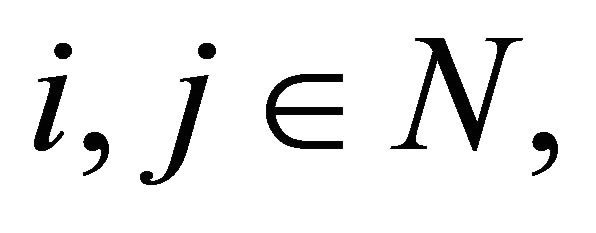
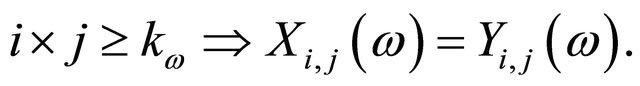 (3.6)
(3.6)
Thus for each 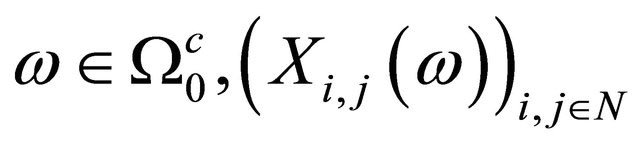 and
and
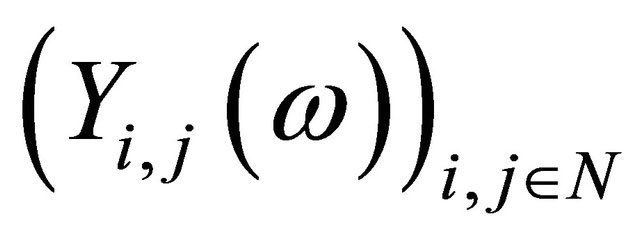 are different only finitely many terms. This implies that (3.3) holds.
are different only finitely many terms. This implies that (3.3) holds.
For fixed 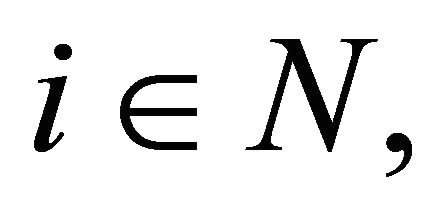 we can find a large
we can find a large 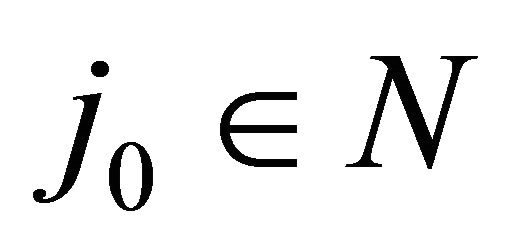 such that (3.6) holds for all
such that (3.6) holds for all 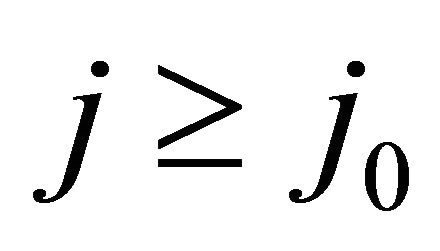 which means that there are only finitely many different terms of
which means that there are only finitely many different terms of 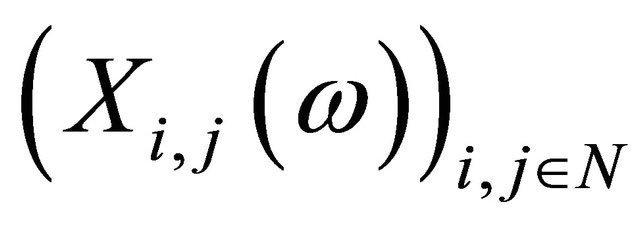 and
and  So for fixed
So for fixed 
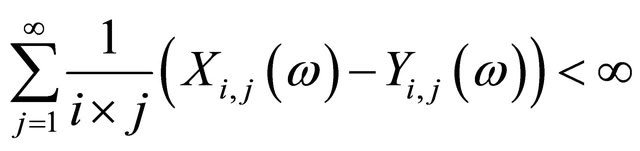 .
.
Similarly, for fixed 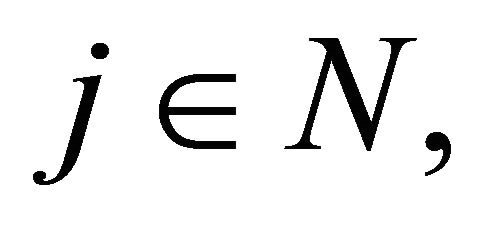
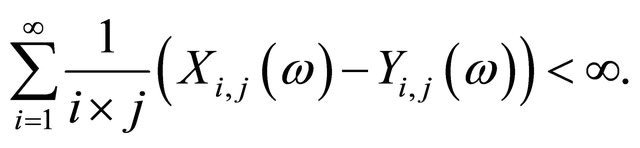
Now (3.4) and (3.5) are now proved and this ends the proof.
Remark 3.1. In case of m fixed and  by considering the limit as
by considering the limit as 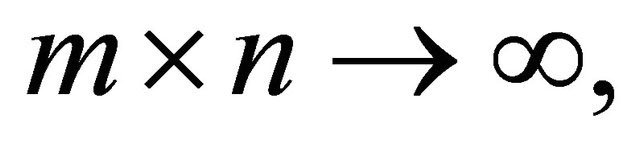 we also obtain the corresponding results for a case of 1-dimensional pairwise ND random variables.
we also obtain the corresponding results for a case of 1-dimensional pairwise ND random variables.
4. Example
Example 4.1 A box contains pq balls of p different colors and q different sizes in each color. Pick 2 balls randomly.
Let 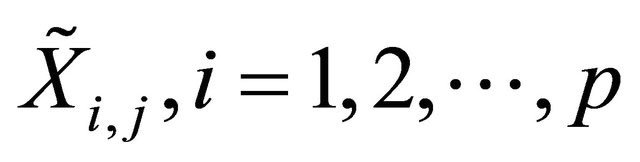 and
and 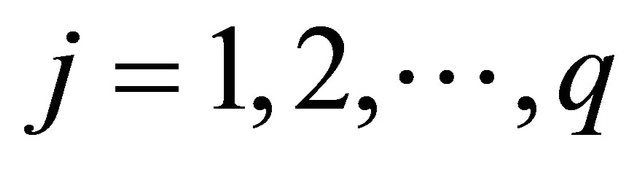 be a random variable indicating the presence of a ball of the ith color and the jth size such that
be a random variable indicating the presence of a ball of the ith color and the jth size such that

For 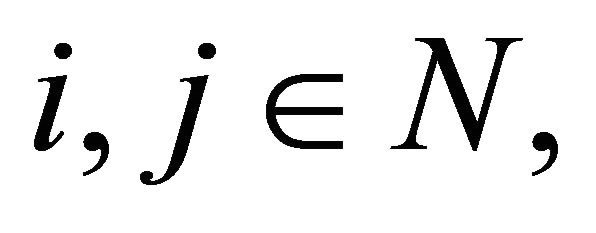 let
let 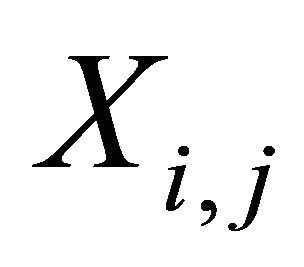 be a random variable defined by
be a random variable defined by

Proof. By a direct calculation, we have ’s are pairwise ND random variables, i.e. for
’s are pairwise ND random variables, i.e. for 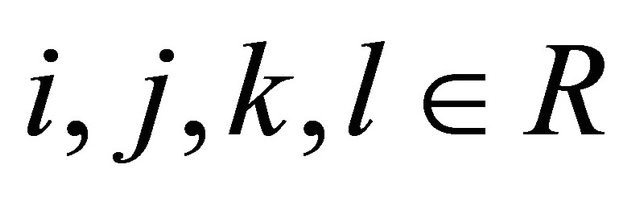 that
that 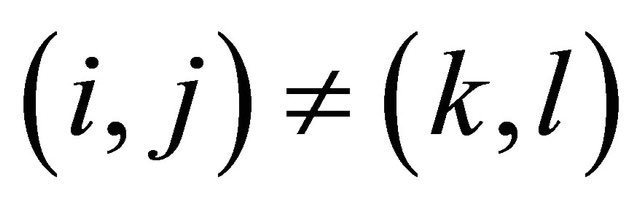 and
and 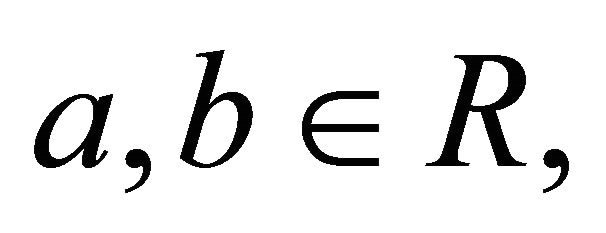
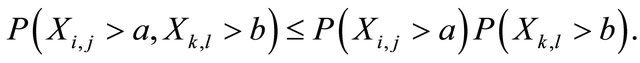
Note that
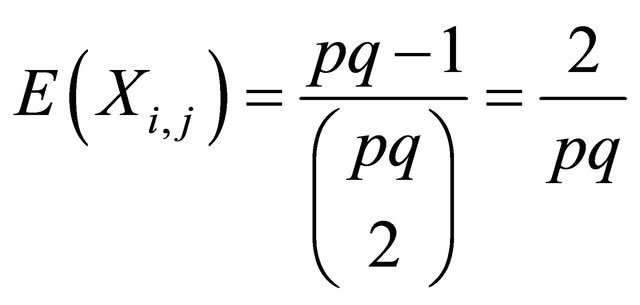
and 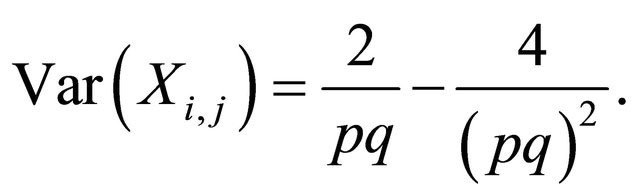
Hence,
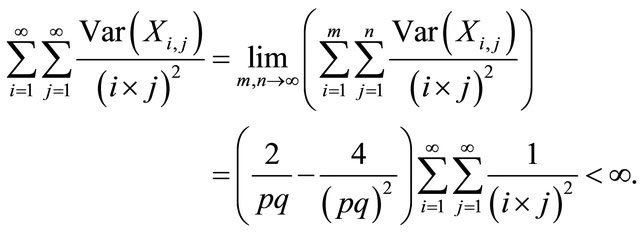
By applying Theorem 1.6, for any double sequence 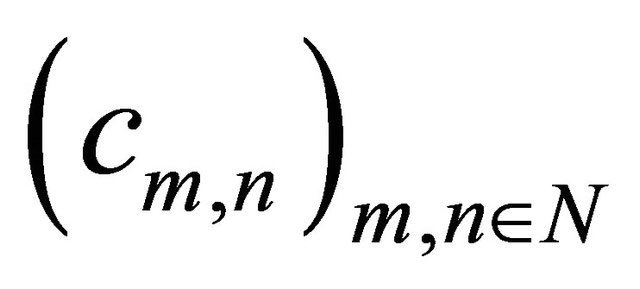 such that
such that 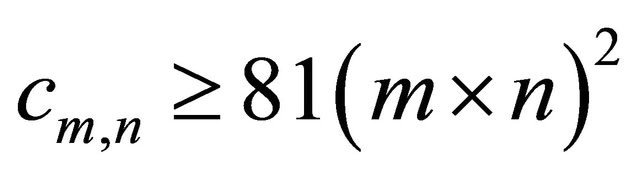 for every m
for every m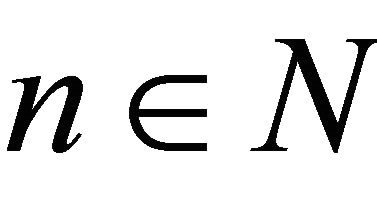 , we have
, we have 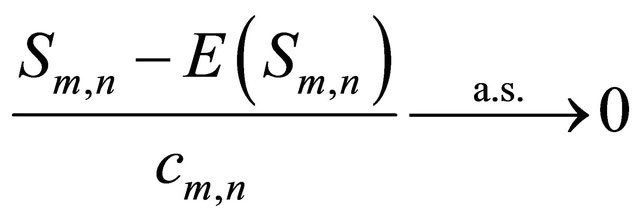 as
as ![]()
5. Acknowledgements
The authors would like to thank referees for valuable comments and suggestions which have helped improving our work. The first author gives an appreciation and thanks to the Institute for the Promotion of Teaching Science and Technology for financial support.
REFERENCES
- S. Csörgő, K. Tandori and V. Totik, “On the Strong Law of Large Numbers for Pairwise Independent Random Variables,” Acta Mathematica Hungarica, Vol. 42, No. 3- 4, 1983, pp. 319-330. doi:10.1007/BF01956779
- N. Etemadi, “An Elementary Proof of the Strong Law of Large Numbers,” Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, Vol. 55, No. 1, 1981, pp. 119-122.
- R. G. Laha and V. K. Rohatgi, “Probability Theory,” John Wiley & Sons, Hoboken, 1979.
- T. Birkel, “A Note on the Strong Law of Large Numbers for Positively Dependent Random Variables,” Statistics & Probability Letters, Vol. 7, No. 1, 1989, pp. 17-20. doi:10.1016/0167-7152(88)90080-6
- H. A. Azarnoosh, “On the Law of Large Numbers for Negatively Dependent Random Variables,” Pakistan Journal of Statistics, Vol. 19, No. 1, 2003, pp. 15-23.
- H. R. Nili Sani, H. A. Azarnoosh and A. Bozorgnia, “The Strong Law of Large Numbers for Pairwise Negatively Dependent Random Variables,” Iranian Journal of Science & Technology, Vol. 28, No. A2, 2004, pp. 211-217.
- T. S. Kim, H. Y. Beak and H. Y. Seo, “On Strong Laws of Large Numbers for 2-Dimensional Positively Dependent Random Variables,” Bulletin of the Korean Mathematical Society, Vol. 35, No. 4, 1998, pp. 709-718.
- T. S. Kim, H. Y. Beak and K. H. Han, “On the Almost Sure Convergence of Weighted Sums of 2-Dimensional Arrays of Positive Dependent Random Variables,” Communications of the Korean Mathematical Society, Vol. 14, No. 4, 1999, pp. 797-804.
- F. Móricz, “The Kronecker Lemmas for Multiple Series and Some Applications,” Acta Mathematica Academiae Scientiarum Hungaricae, Vol. 37, No. 1-3, 1981, pp. 39- 50. doi:10.1007/BF01904871
- N. Ebrahimi and M. Ghosh, “Multivariate Negative Dependence,” Communications in Statistics—Theory and Methods, Vol. A10, No. 4, 1981, pp. 307-337.
- K. L. Chung, “A Course in Probability Theory,” Academic Press, London, 2001.

