Open Journal of Statistics
Vol. 2 No. 5 (2012) , Article ID: 25546 , 6 pages DOI:10.4236/ojs.2012.25064
The First Order Autoregressive Model with Coefficient Contains Non-Negative Random Elements: Simulation and Esimation
Military Technical Academy, Hanoi, Vietnam
Email: van_khanh1178@yahoo.com
Received October 14, 2012; revised November 14, 2012; accepted November 27, 2012
Keywords: Random Coefficient Autoregressive Model; Quasi-Maximum Likelihood; Consistency
ABSTRACT
This paper considered an autoregressive time series where the slope contains random components with non-negative values. The authors determine the stationary condition of the series to estimate its parameters by the quasi-maximum likelihood method. The authors also simulate and estimate the coefficients of the simulation chain. In this paper, we consider modeling and forecasting gold chain on the free market in Hanoi, Vietnam.
1. Introduction
It is well-known that many time series in finance such as stock returns exhibit leptokurtosis, time-varying volatility and volatility clusters. The generalized autoregressive conditional heteroscedasticity (GARCH) and the random coefficient autoregressive (RCA) model have been caturing three characteristics of financial returns.
The RCA models have been studied by several authors [1-3]. Most of their theoreic properties are well-known, including conditions for the existence and the uniqueness of a stationary solution, or for the existence of moments for the stationary distribution. In this paper, we address the stationary conditions for the RCA model, the existence and the uniqueness of a stationary solution and parameter estimation problem for the RCA model with the coefficient have a non-negative random elements.
2. Stationary Conditions of the Series
Consider time series 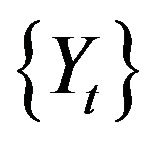 satisfying
satisfying
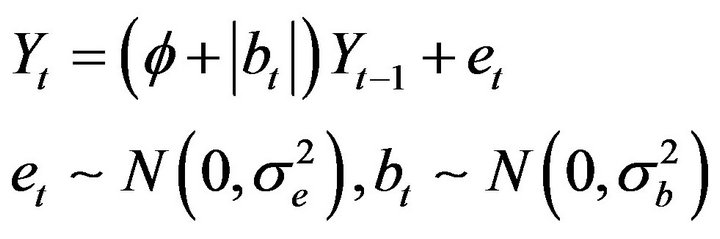 (1)
(1)
where 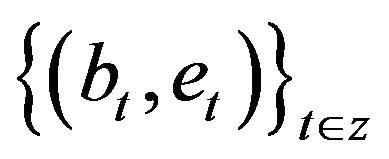 are random vectors with independent identical distribution defined in a certain
are random vectors with independent identical distribution defined in a certain 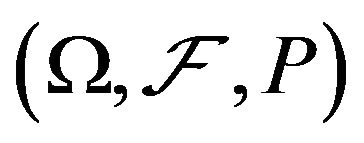 probability space(2)
probability space(2)
Firstly, we consider the property of the stochastic variable
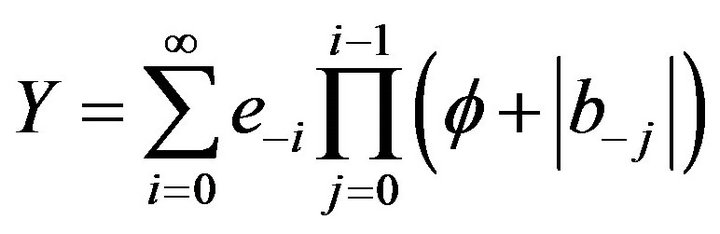 (3)
(3)
Let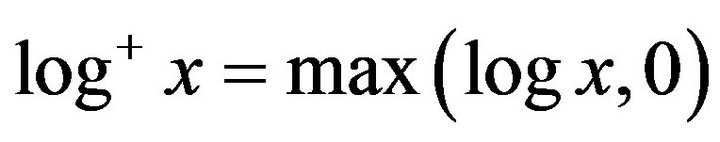 .
.
Lemma 1. Suppose that condition (2) satisfied,
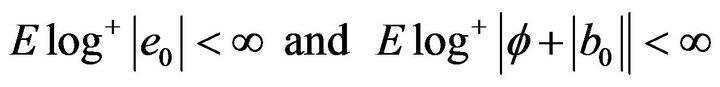 (4)
(4)
If
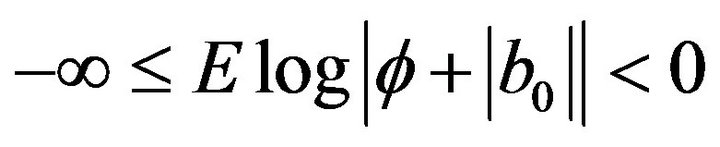 (5)
(5)
Y determined by (3) will be absolute convergence with probability 1.
Proof.
Assume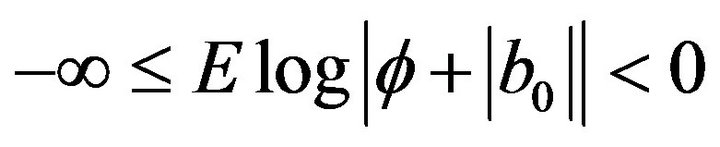 , according to the law of great numbers, existing stochastic variable
, according to the law of great numbers, existing stochastic variable 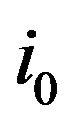 such that:
such that:
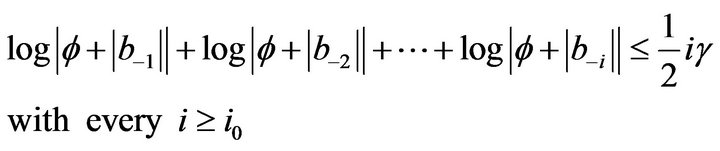 (6)
(6)
where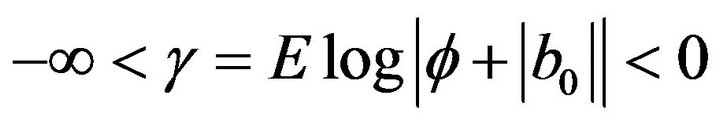 . Then
. Then
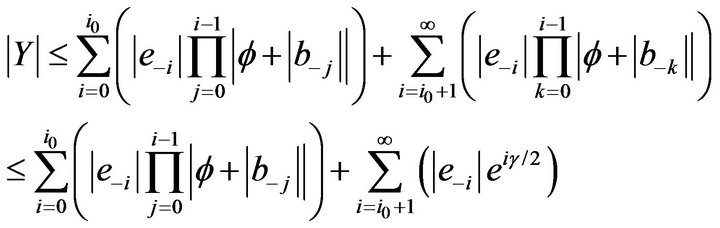 (7)
(7)
We will prove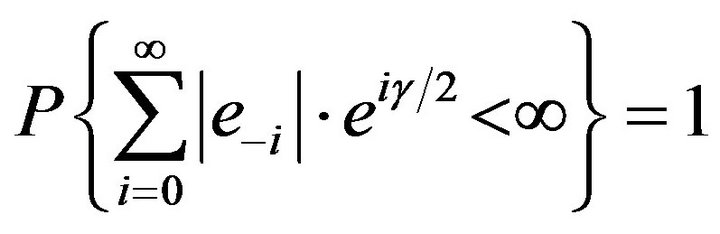 . Indeed, due to
. Indeed, due to
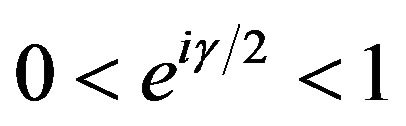 and in accordance with lemma Borel-Cantelli, sufficient condition here means proving
and in accordance with lemma Borel-Cantelli, sufficient condition here means proving
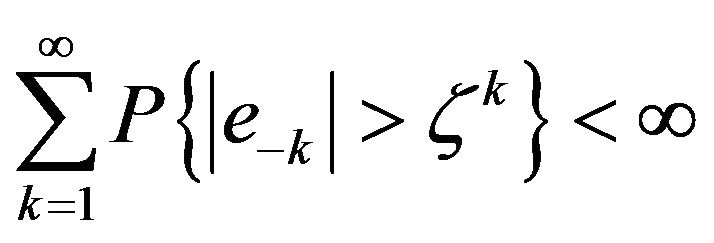 with
with  We have:
We have:
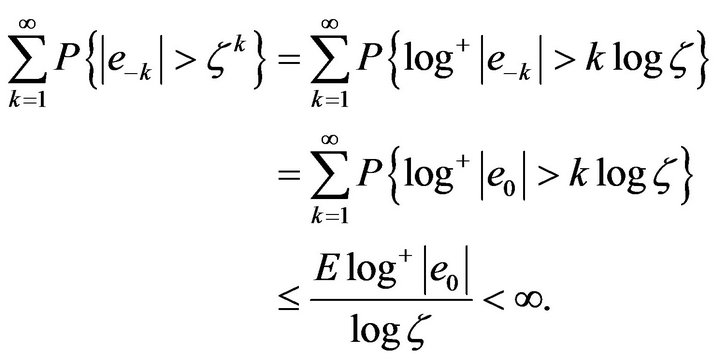
From (7), we have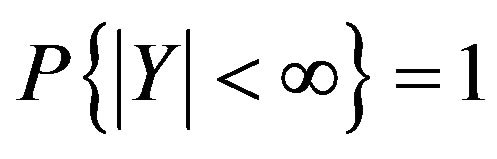 .
.
If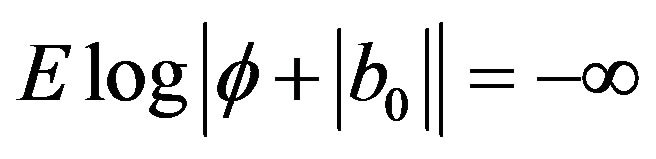 , (6) can always correct with some
, (6) can always correct with some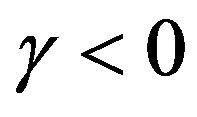 . Therefore, (7) is always true.
. Therefore, (7) is always true.
Lemma 2. Suppose that (2) and (5) meet
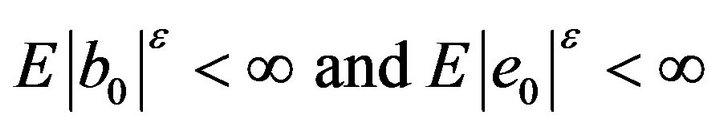 with some
with some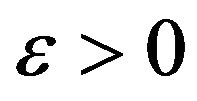 . Then, existing
. Then, existing 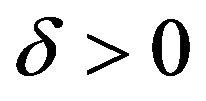 such that
such that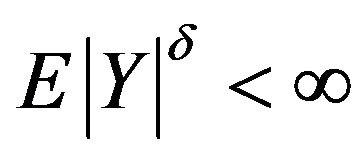 .
.
Proof.
Suppose 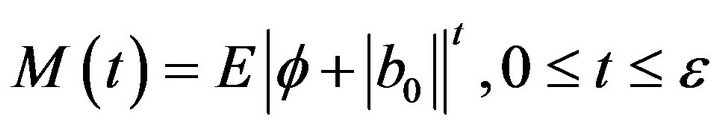
We have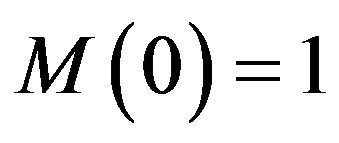 , and owing to
, and owing to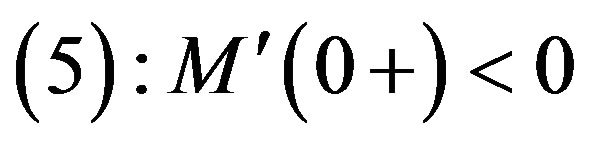 ,
, 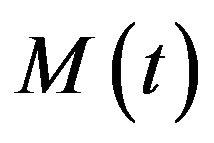 is a decreasing function in the neighborhood of 0. Hence, existing
is a decreasing function in the neighborhood of 0. Hence, existing 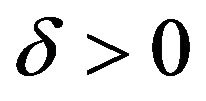 such that
such that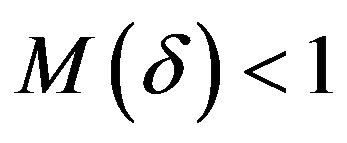 . Generally less, suppose that
. Generally less, suppose that 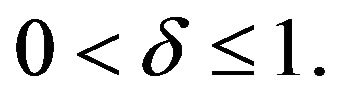 Due to the convex, we have
Due to the convex, we have 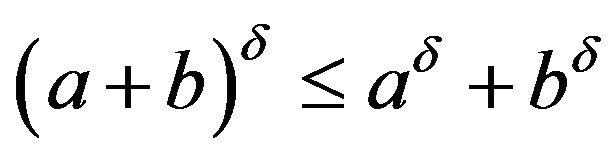 với
với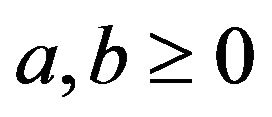 .
.
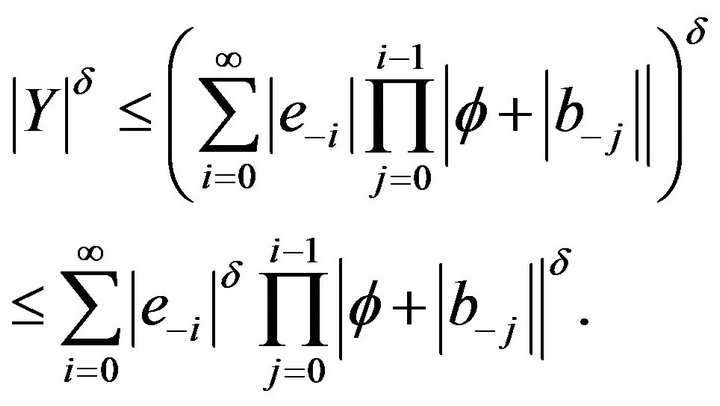
Use condition (2) and , we obtain:
, we obtain:
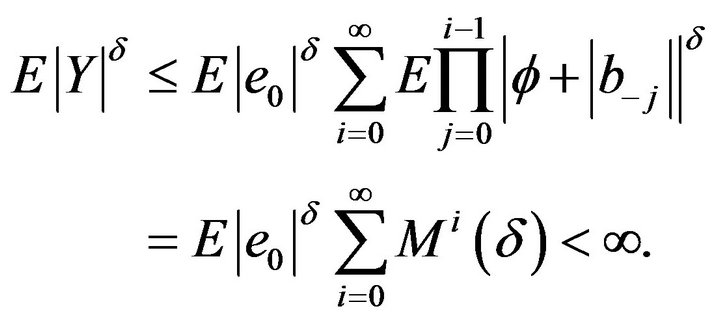
Lemma 3. Assume (2) and (5) are satisfied with
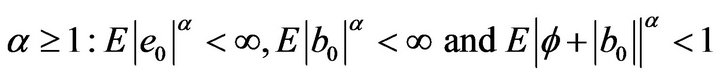 . Then
. Then
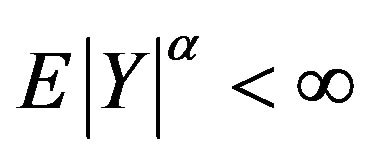 .
.
Proof.
Due to condition (2) and inequality Minkowski
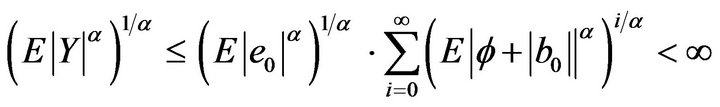 . Hence,
. Hence,
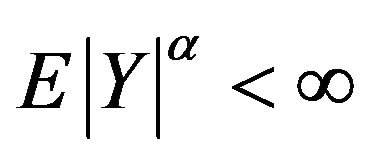 .
.
Theorem 1: Suppose that (1), (4) and (5) satisfied with the almost sure convergence of
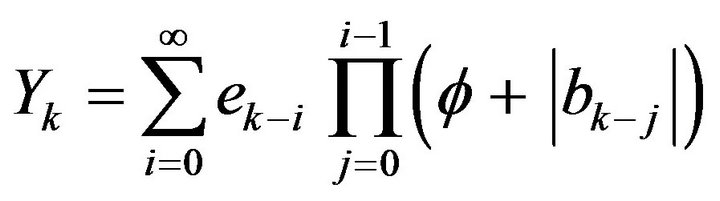 and process
and process 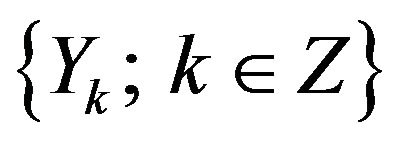 is the stationary solution of (1)
is the stationary solution of (1)
Proof.
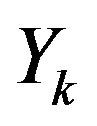 is convergent absolutely, acording to Lemma 1 We have:
is convergent absolutely, acording to Lemma 1 We have: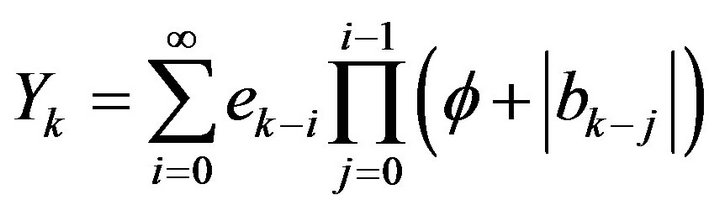 . Therefore:
. Therefore:

 is the single solution of (1)
is the single solution of (1)
Obviously, 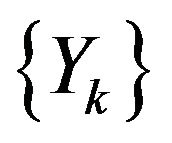 is a stationary series and
is a stationary series and 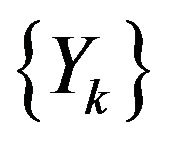 is independent of
is independent of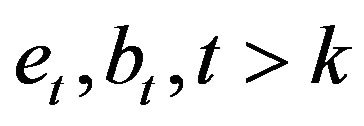 .
.
3. Estimation of Model Parameters
Suppose that

In this section, we care about estimating vectors of 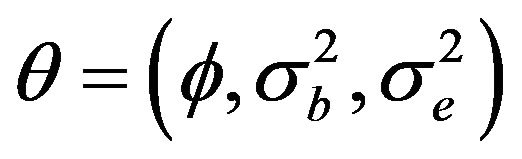 based on Quasi-Maximum Likelihood method.
based on Quasi-Maximum Likelihood method.
With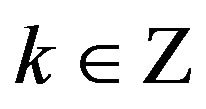 , we have:
, we have:

but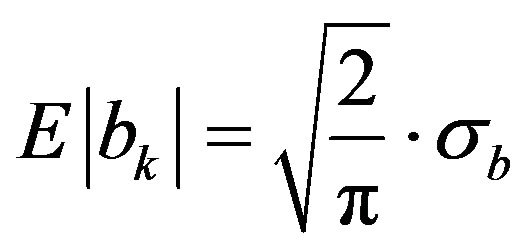 , so
, so
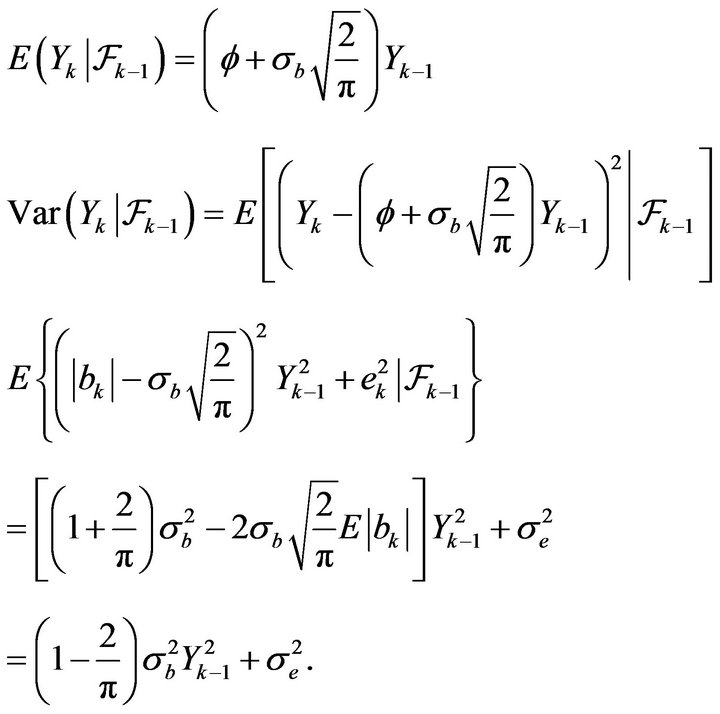
Therefore, we have following likelihood function
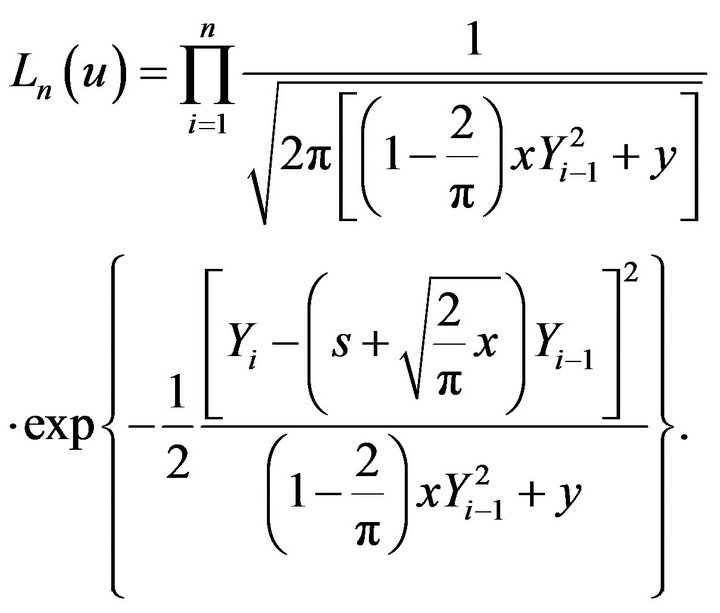
Maximum likelihood estimators determined by:
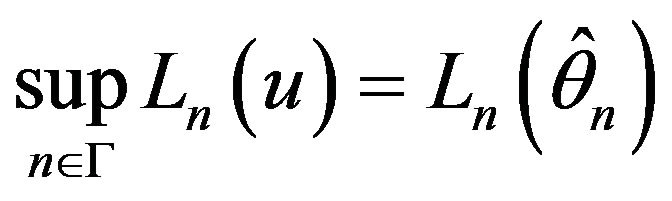 (8)
(8)
where ![]() is a certain optional appropriate area of
is a certain optional appropriate area of 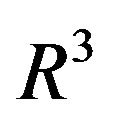
Let
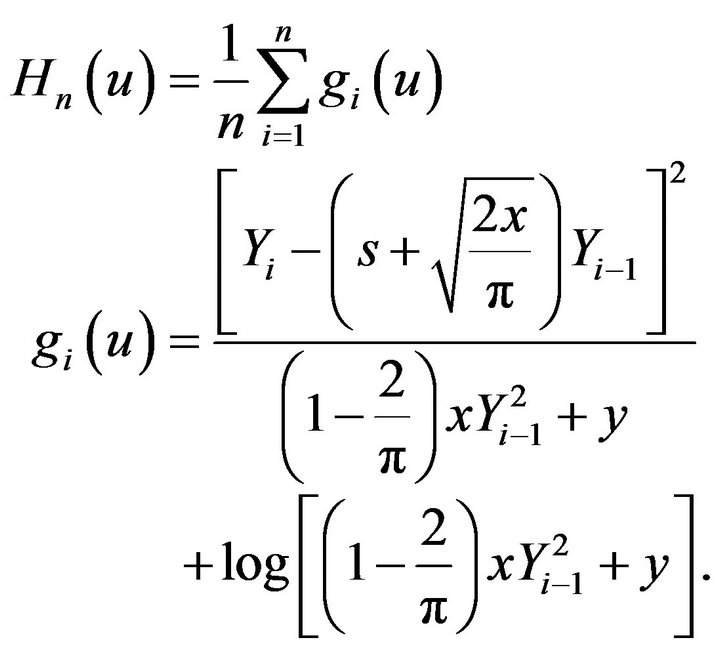
Then (8) can be written as 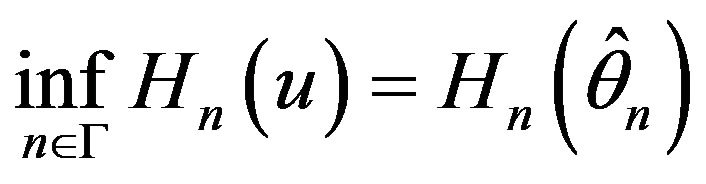
Assume
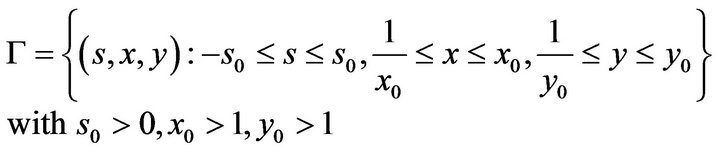 (9)
(9)
Now, the consistence of maximum livelihood estimates 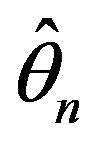 is said.
is said.
Theorem 2. Suppose (2), (4), (5), (8), (9) satisfied and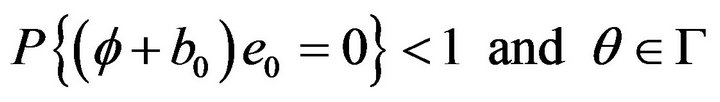 . We have
. We have
 .
.
Proof.
Let

and 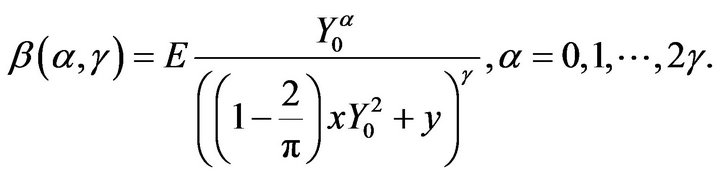
We will prove ![]() be continuous on
be continuous on![]() .
.
Indeed,

On the other hand,
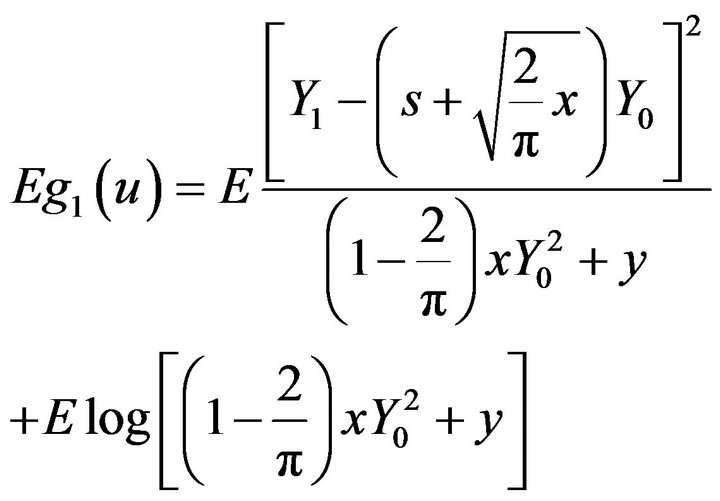
But
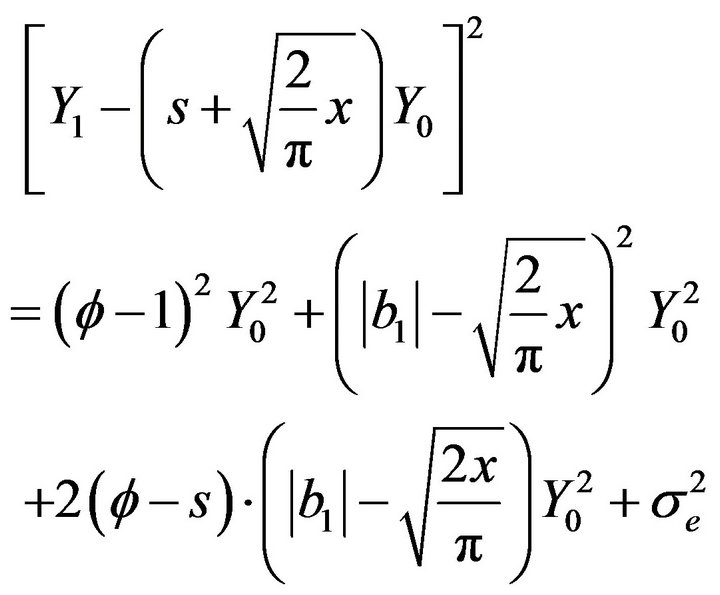
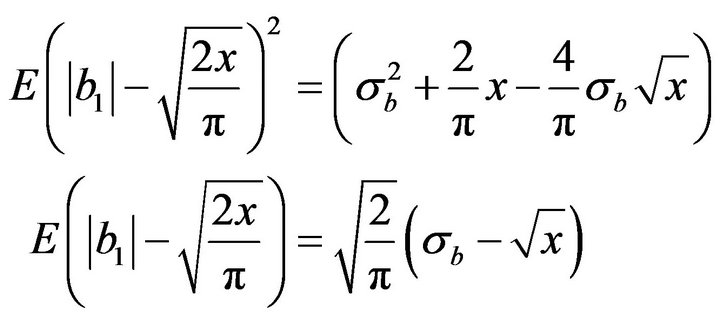
Then
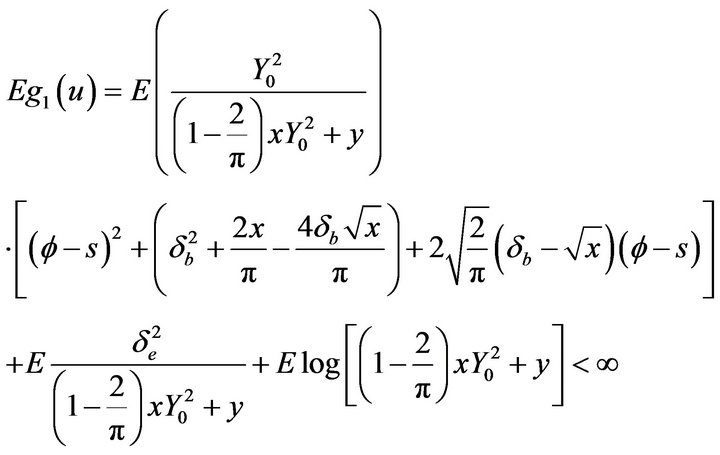
 is a continuous function in acordance with
is a continuous function in acordance with
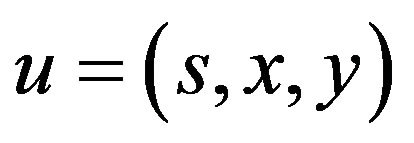 . Next, we will prove:
. Next, we will prove:
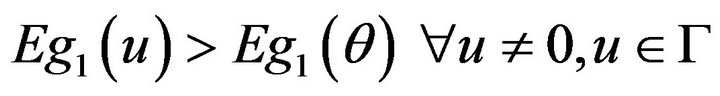 .
.
In fact,
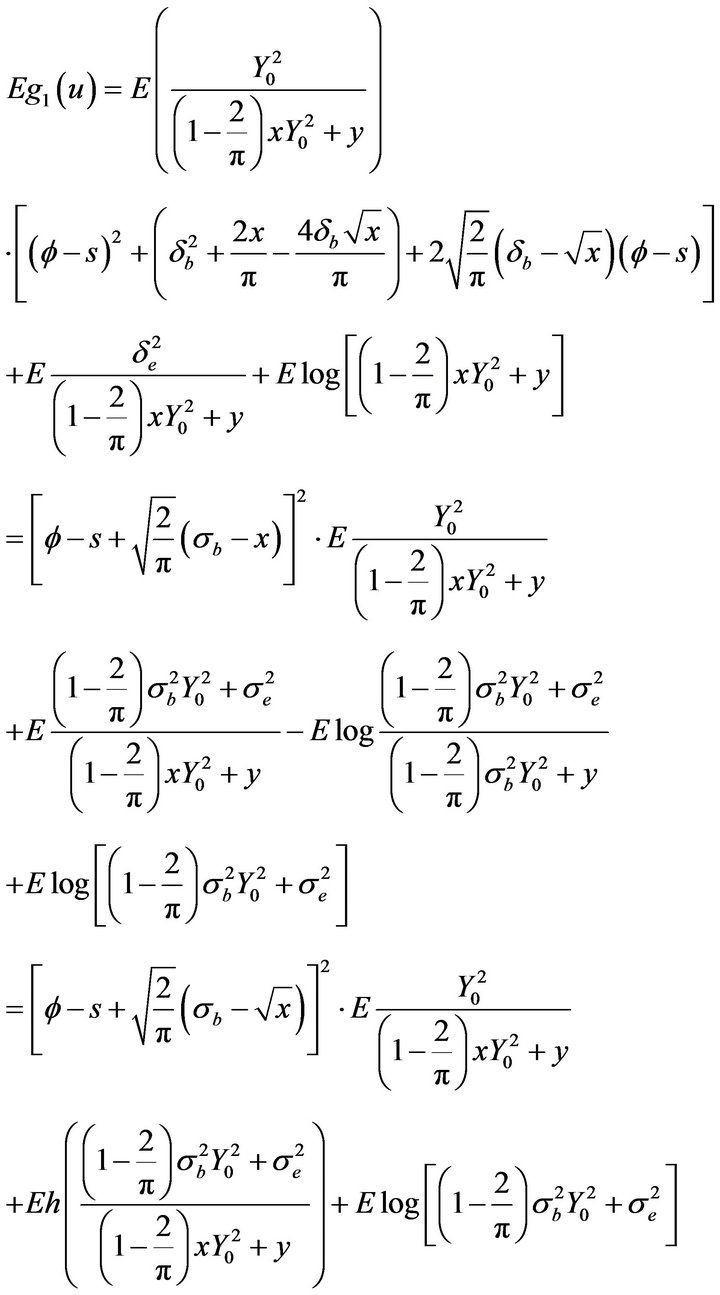
where
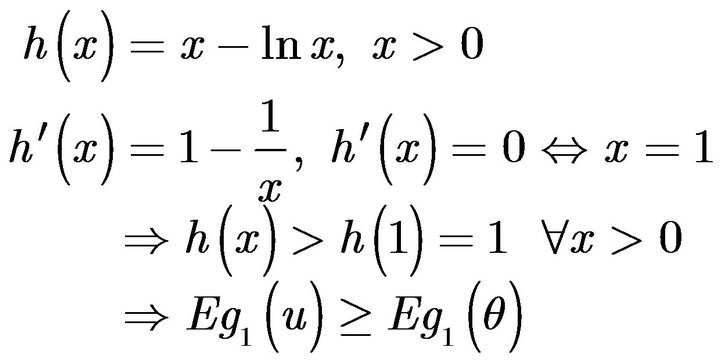
and 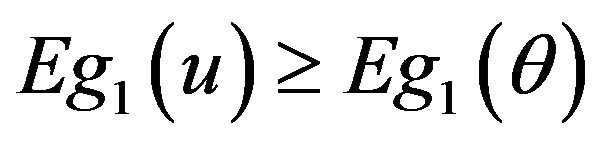 if and only if
if and only if
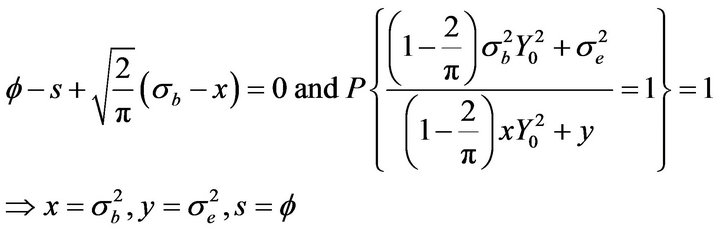
If
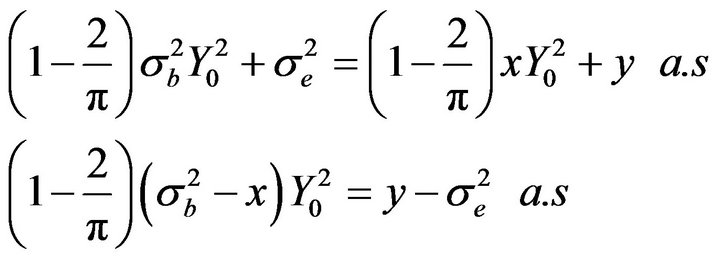 If
If 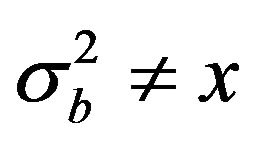 or
or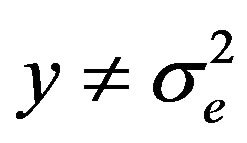 ,
, 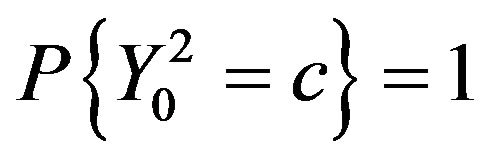
But 
But 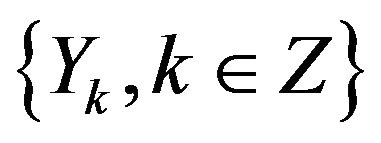 is a stationary series
is a stationary series
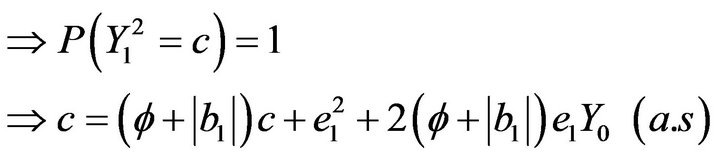
But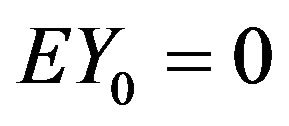 , take conditional expectations
, take conditional expectations 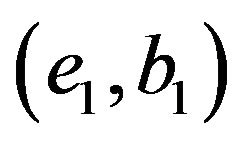 in both sides, we have:
in both sides, we have:
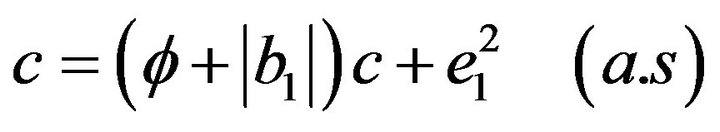
But 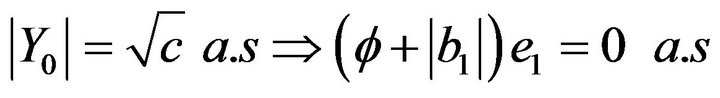
Return to theorem![]() , so
, so
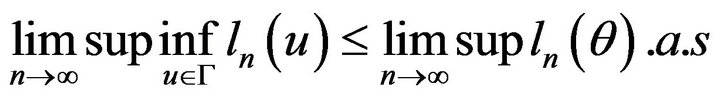
But series 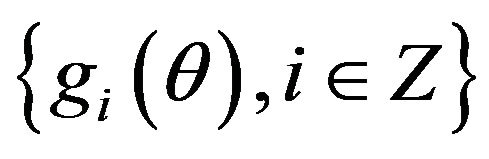 is stationary and ergodic with
is stationary and ergodic with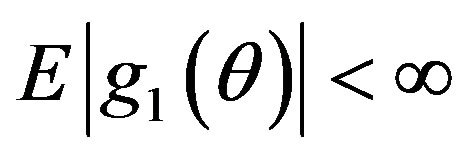 , according to Ergodic theorem, we have:
, according to Ergodic theorem, we have:
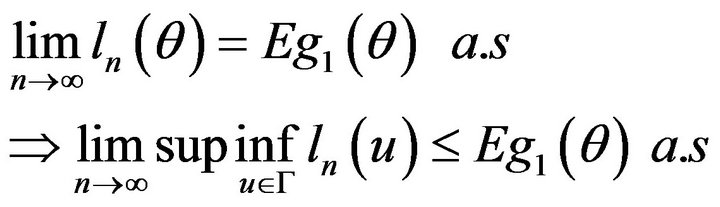
With each positive integer 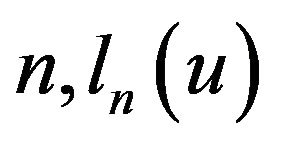 is a continuous function in compact set G, so
is a continuous function in compact set G, so
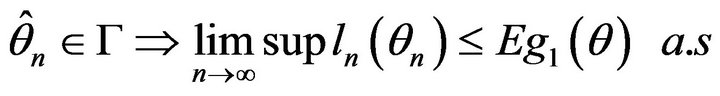
Let 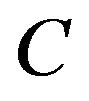 -compact set in
-compact set in ![]() with positive distance to
with positive distance to . Owing to g1(u) being continuous in
. Owing to g1(u) being continuous in![]() , existing an open sphere U(u) with center u with
, existing an open sphere U(u) with center u with 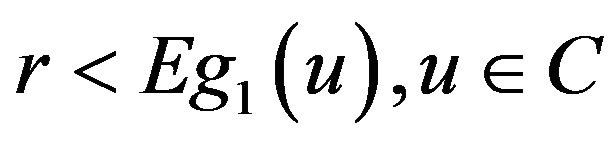 such that:
such that:
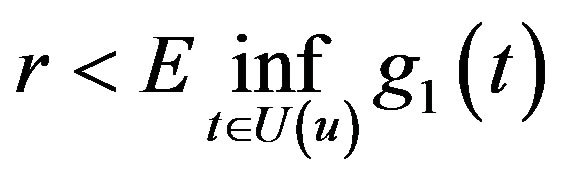 .
.
Sets 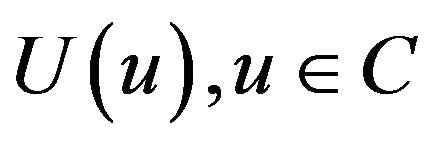 are open covers of C, so C holds such finite open covers, are called
are open covers of C, so C holds such finite open covers, are called 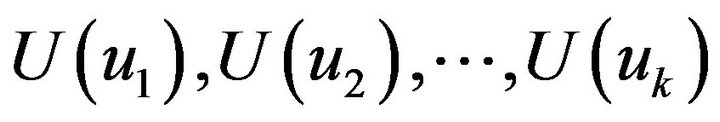 of C. In accordance with Ergodic thoerem, with every
of C. In accordance with Ergodic thoerem, with every , we have:
, we have:
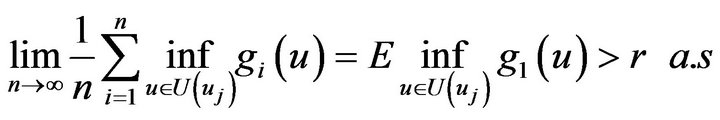
See that

In out of events 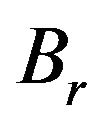 with
with 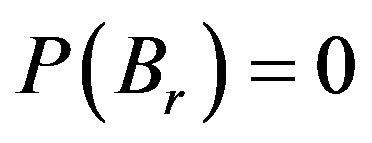 with
with 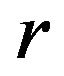 satisfying:
satisfying:![]() .
.
Therefore, ![]()
But  is continuous and
is continuous and 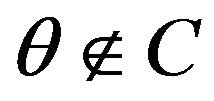 is singly minimum of
is singly minimum of 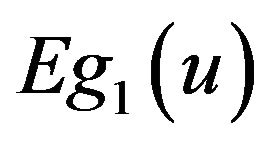
![]()
Let U is a open sphere with center  and enough small radius and
and enough small radius and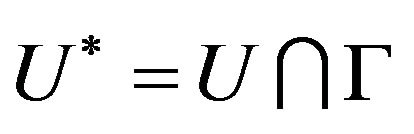 . If
. If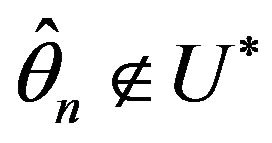 , existing a random subseries
, existing a random subseries 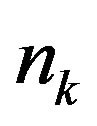 such that with
such that with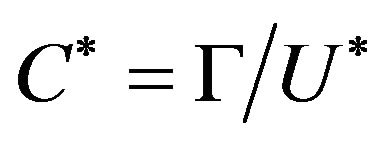 , we have:
, we have:
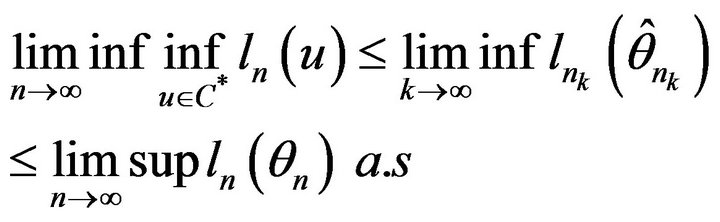
But 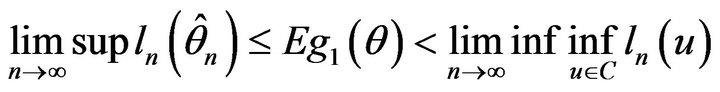
hence, with each above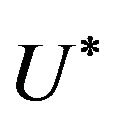 , existing random variable
, existing random variable 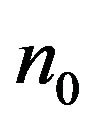 such that
such that 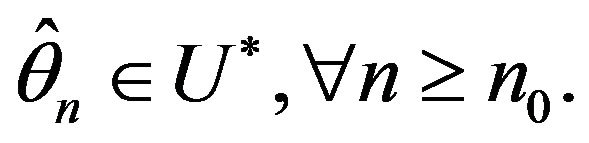
This completes the proof. 
4. Simulation
In this section, we simulate series (1) with different values of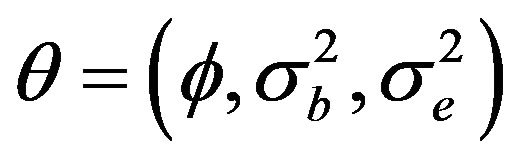 . These simulations show stationary and non-stationary series cases.
. These simulations show stationary and non-stationary series cases.
We simulate series (1) with different values of 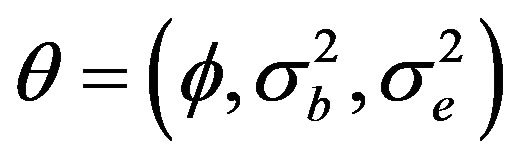 and in each case we can check the stationary conditions of the series (1) by Lemma 1. In Figure 1, we see that the series is not stationary with the negagtive slope
and in each case we can check the stationary conditions of the series (1) by Lemma 1. In Figure 1, we see that the series is not stationary with the negagtive slope  and in Figures 2 and 3 we simulate the not stationary series with positive slope
and in Figures 2 and 3 we simulate the not stationary series with positive slope 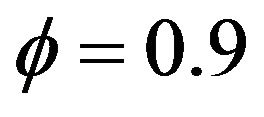 and
and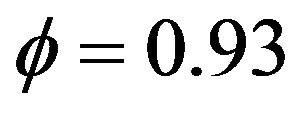 . Figure 4 presents a stationary but clustering series, Figures 5-7 present stationary series with parameters are
. Figure 4 presents a stationary but clustering series, Figures 5-7 present stationary series with parameters are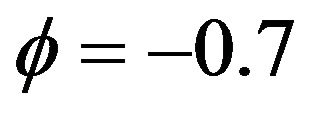 ,
, 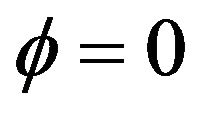 and
and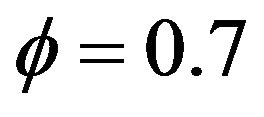 .
.
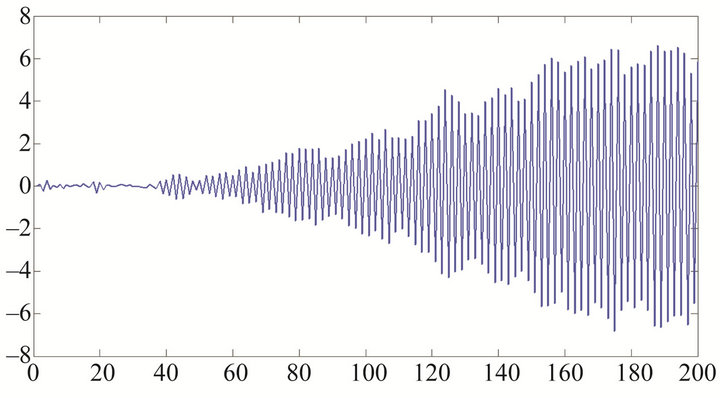
Figure 1. Simulation for series Yt defined by (1) with![]() .
.
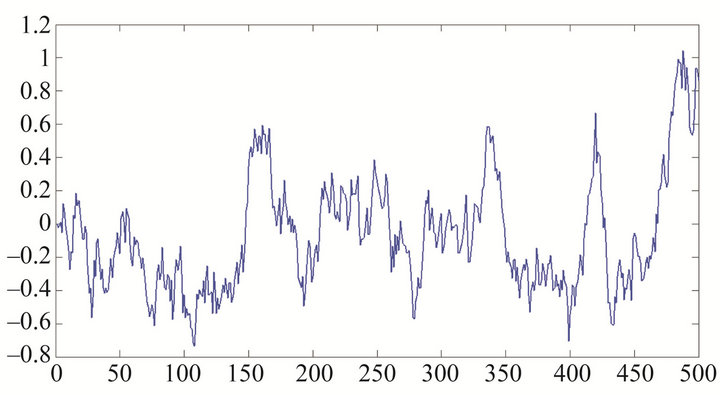
Figure 2. Simulation for series Yt defined by (1) with![]() .
.
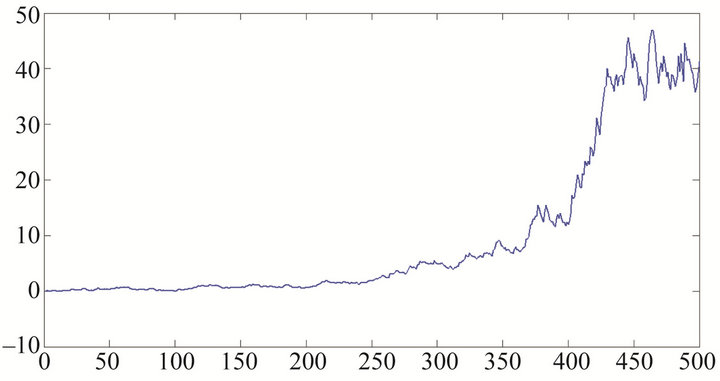
Figure 3. Simulation for series Yt defined by (1) with![]() .
.
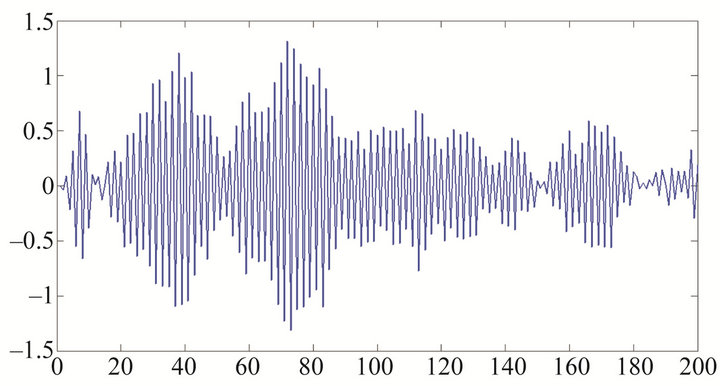
Figure 4. Simulation for series Yt defined by (1) with![]() .
.
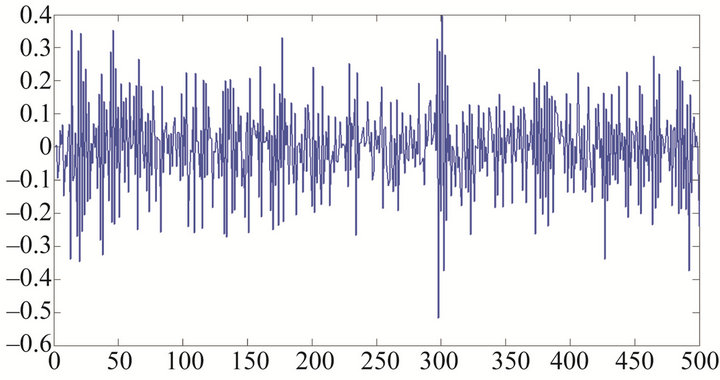
Figure 5. Simulation for series Yt defined by (1) with![]() .
.
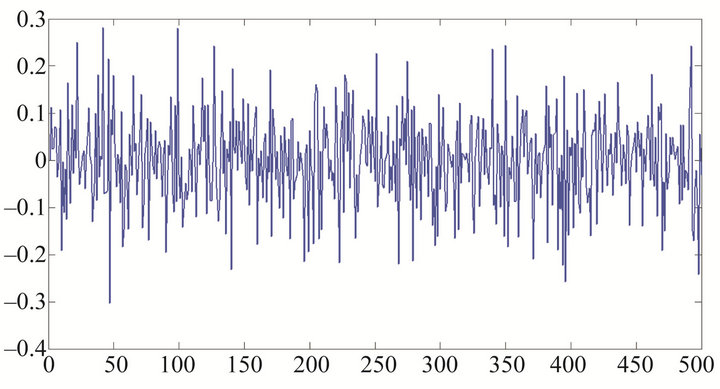
Figure 6. Simulation for series Yt defined by (1) with![]() .
.
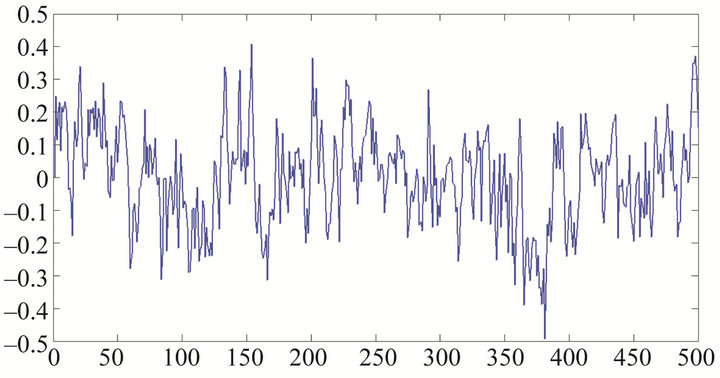
Figure 7. Simulation for series Yt defined by (1) with![]() .
.
5. Application for Real-Time Series
In this section, we use model (1) for the model of return series of the price of gold on the free market in Hanoi, Vietnam. Figure 8 show the Return series of Gold price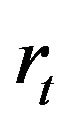 .
.
From the data series we estimate for vector
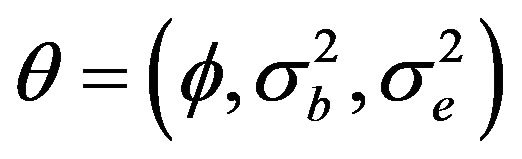 is
is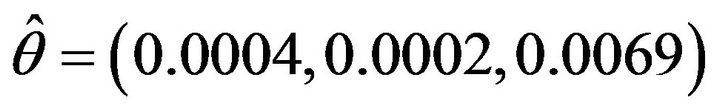 . So, we can use the following model to forecast the future value of gold price:
. So, we can use the following model to forecast the future value of gold price: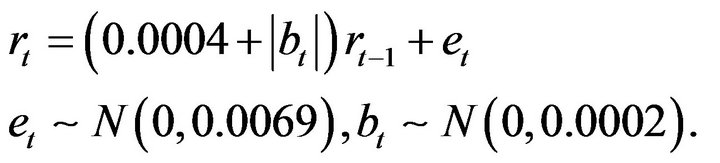
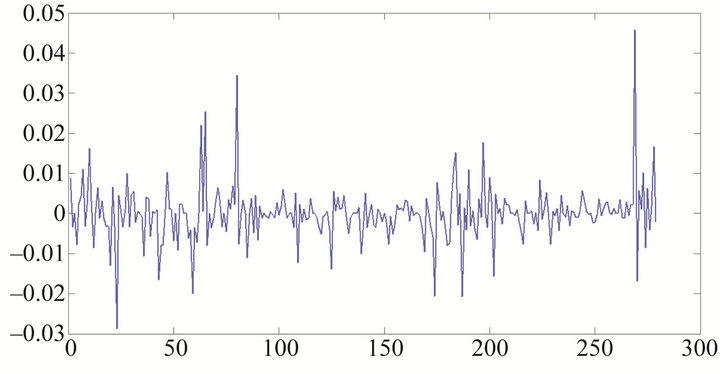
Figure 8. Return series of Gold price rt.
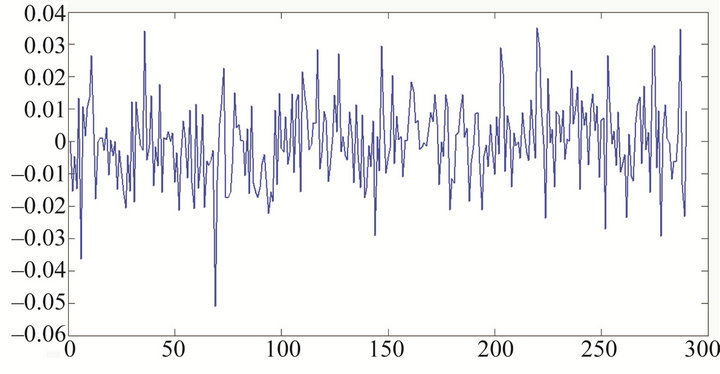
Figure 9. Simulation for series Yt defined by (1) with![]() .
.
Figure 9 below is a simulation of the process (1) with parameters .
.
6. Conclusion
This paper has solved some problems relating to a kind of first order time series with coefficient regression affected by non-negative random elements. In subsequent studies, the author will consider the asymptotic estimates of the parameters.
REFERENCES
- T. Bollerslev, “Generalized Autoregressive Conditional Heteroscedasticity,” Journal of Econometrics, Vol. 31, No. 3, 1986, pp. 307-327. doi:10.1016/0304-4076(86)90063-1
- D. Nicholls and B. Quinn, “Random Coefficient Autoregressive Models: An Introduction,” Springer, New York, 1982. doi:10.1007/978-1-4684-6273-9
- A. Aue, L. Horvath and J. Steinbach, “Estimation in Random Coefficient Autoregressive Models,” Journal of Time Series Analysis, Vol. 27, No. 1, 2006, pp. 61-76. doi:10.1111/j.1467-9892.2005.00453.x

