ABSTRACT

The acidic dissociation constant of N-(2-acetamido)-iminodiacetic acid monosodium (ADA) has been determined at 12 temperatures from 278.15 to 328.15 K by electromotive-force (emf) measurements of hydrogen-silver chloride cells without liquid junction. At 298.15 K, the value of the dissociation constant (pK₂) is 6.8416 ± 0.0004. In response to the need for new physiological pH standards, buffer solutions of NaADA and its disodium salt, Na₂ADA would be useful for pH control in the biological region of pH 6.5 to 7.5. The pK₂ values over the experimental temperature range are given as a function of the thermodynamic temperature (T) by the equation pK₂ = 2943.784/T − 47.05762 + 7.72703 ln T. At 298.15 K, standard thermodynamic quantities for the dissociation process have been derived from the temperature coefficients; ∆H˚ = 12,252 J∙mol⁻¹, ∆S˚ = −89.9 J∙K⁻¹∙mol⁻¹ and 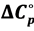/wang#^#Bracket# = −148 J∙K−1∙mol−1. The results are interpreted and compared with those of structurally related derivatives of GLYCINE.

Keywords:Dissociation Constant, ADA, Emf, Buffer, Thermodynamic Quantity

1. Introduction

In earlier work over the temperature range 278.15 to 328.15 K, we have investigated the thermodynamics of the dissociation of a series of N-substituted derivatives of the simplest amino acid, GLYCINE which exists in a zwitterionic form. Included were 2-aminoethanoic acid (GLYCINE) [1] , N-tris(hydroxymethyl)methylglycine (TRICINE) [2] and bis-[(2-hydroxyethyl)amino] acetic acid (BICINE) [3] . We have also studied thermodynamic quantities for the dissociation of a series of some substituted TAURINE such as N-tris[hydroxymethy]-4-aminoethanesulfonic acid (TABS) [4] and (3-[N-morpholino])]-2-hydroxypropanesulfonic acid (MOPSO) [5] from 278.15 to 328.15 K. In order to provide useful pH standard buffer for the control of acidity in the pH range 6.5 to 8.5, which is important for studies of clinical fluids and physiological media of ionic strength I = 0.16 mol∙kg⁻¹, we have undertaken to study acid-base behavior, and to determine values for the second dissociation constant pK₂ and thermodynamic functions of N-(2-acetamido)iminodiacetic acid (ADA) in the temperature range 278.15 K to 328.15 K in an earlier publication [6] . The values of these quantities were reported by using a different galvanic cell without liquid junction of the type:

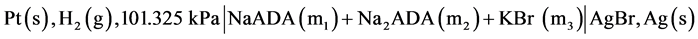(A)

In cell (A) m₁ and m₂ represent molalities of the species. In the present work, we have used a corresponding cell with silver-silver chloride instead of silver-silver bromide electrode and NaCl salt instead of KBr. The desirability of an accurate knowledge of the ionization of ADA is very important. Thus the main objective of using the new cell was to redetermine the pK₂ values and consequently pH values in isotonic saline solution containing NaCl, which is a major component in blood. The following cell was used in the present study:

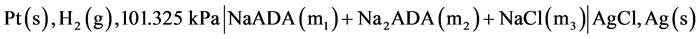(B)

In 1966, Good et al. [7] recommended several zwitterionic buffer compounds which are compatible with common physiological media. The buffer compound N-(2-Acetamido)-iminodiacetic Acid Monosodium (ADA) was included in the list for biological buffers in the pH range of clinical fluids. The pK₂ values have been determined at twelve temperatures from 278.15 to 328.15 K by measuring the emf of cell (B). At 298.15 K, the pK₂ is 6.8416 compared to 6.844 [6] using Ag-AgBr electrode. The results are in good agreement. The dissociation process step, involving the deprotonation of the substituted ammonium group of ADA itself, can be represented by the following equation:

(1)

where K₂ is the thermodynamic equilibrium constant. The zwitterion structure of the buffer ADA is shown below (Figure 1).

2. Experimental Section

The commercial sample of ADA was obtained from Research Organics, Inc. The analysis of the purified sample averaged 99.9%. The usual method of purification has been described earlier [6] [8] . From preliminary measurements the difference in emf data using both purified and unpurified ADA buffer was within ± 0.03 mV. Thus the unpurified sample was dried and stored in a desiccator over drierite. All buffer solutions were prepared by mixing requisite quantities of monosodium ADA, ACS certified reagent grade NaCl, standard carbonate-free NaOH solution and carbon dioxide free, twice distilled, deionized water. Vacuum corrections were applied to all masses. The design of all glass cells [9] , the method of preparation of hydrogen electrode and the silver-silver chloride electrodes (thermal electrolytic type) [10] and the purification of the hydrogen gas, and other experimental details have been described in earlier publications [11] . The temperature was regulated to within ± 0.005 K by means of a digital thermometer (guideline model 9540).

3. Method

The precise emf measurement technique was originally used by Harned and Ehlers [12] . In the present work, we

have used modified version of Gary et al. [9] . All measurements were made by using hydrogen electrodes and the silver-silver chloride electrodes at 12 temperatures at an interval of 5 K from 278.15 K to 328.15 K including body temperature, 310.15 K. Initial emf measurements were always made at 298.15 K, allowing about 2 hours for equilibrium to be attained. The following cell without liquid junction was used:

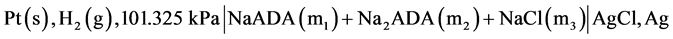(B)

where m₁, m₂ and m₃ indicate the molalities of NaADA, Na₂ADA, and NaCl, respectively. The values of m₁, m₂ and m₃ range from 0.002, 0.007, 0.002 up to m₁ = 0.03157, m₂ = 0.01052, and m₃ = 0.03491 mol∙kg⁻¹, respectively. At 298.15 K, the emf readings in the beginning and in the middle on the average, were within ± 0.03 mV. The emf measurements were made in duplicate for almost all cases. The experimental emf values for all 16 buffer solutions were corrected to a hydrogen partial pressure of 1 atm (101.325 kPa). These values are listed in Table 1.

4. Results

The “apparent” thermodynamic dissociation constant for the cell (B) is expressed as:

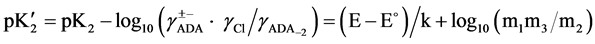(2)

where ADA^±− is the NaADA; ADA⁻² stands for Na₂ADA; m is the molality of the corresponding species shown in cell (B); pK₂ is the thermodynamic dissociation constant; k = 0.059156 V; γ the activity coefficient; E the emf corrected to a hydrogen partial pressure of 1 atm; and E˚ is the standard electrode potential of the (silver + silver chloride) electrode. The values of E˚ have been listed in a recent publication [13] . The activity coefficient term of Equation (2) is small and a function of the ionic strength I, and varies linearly with I. The hydrolysis corrections of m₁/m₂ are negligible because of the pH of buffer solutions of NaADA and Na₂ADA is very close to neutrality. In the present study this observation is consistent with other investigations of structurally related buffer compounds [3] [4] . The ionic strength of the solution for cell (B) is indicated by:

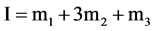(3)

and the simplified Equation (3) is given by:

ßI                                    (4)

As expected varies linearly with I at each temperature. The intercept at I = 0 (infinite dilution) yields the value of pK₂. These values of pK₂, the slope parameters ß, together with their standard deviations, are entered in Table 2. All experimental values of pK₂ from Table 2 were fitted to an equation of the Ives and Moseley form [14] by the method of least squares. Between 278.15 to 328.15 K, pK₂ is given by the expression:

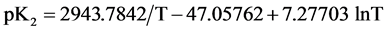(5)

where T is the thermodynamic temperature in Kelvin. The standard deviation for regression of the observed results from Equation (5) is ± 0.00037. The change of Gibbs free energy (∆G˚), enthalpy (∆H˚), entropy (∆S˚) and the heat capacity () for the dissociation of 1 mole of NaADA salt in the standard state were computed from the constants of Equation (5) and applying usual thermodynamic relationships. The results along with the standard deviation of regression estimated by the method of Please [15] , are entered in Table 3. The thermodynamic quantities at 298.15 K for the dissociation of (GLYCINE) [1] and some substituted GLYCINES such as, (BICINE) [3] , (TRICINE) [2] , (N,N-dimethyglycine) [16] , and (ADA) [6 and this work] are compiled in Table 4.

5. Discussion

It is interesting to compare the values of thermodynamic quantities of some structurally related components which are N-substituted GLYCINES. At 298.15 K, these values are shown in Table 4. The parent compound (GLYCINE) [1] has a pK₂ of 9.780 and whereas for (TRICINE) [2] is 8.135 and that for (BICINE) [3] is 8.333. It is evident from Table 4 that the substitution of -(CH₂CH₂OH)₃ group for TRICINE and -(CH₂CH₂OH)₂ group for BICINE decrease acidic strength (lowering of pK₂) for the dissociation of H⁺ from the 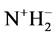group in both compounds. The inductive and steric effects of the oxygen atoms present in hydroxyl groups are attributed to the

^aUnits of m, mol∙kg⁻¹.

^aStandard deviation of pK₂ and ^bslope parameter.

Units: ∆G˚, ∆H˚, J∙mol⁻¹; ∆S˚, 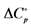, J∙K⁻¹∙mol⁻¹.

^aAg-AgBr electrode used; ^bAg-AgCl electrode used; Units: ∆H˚, J∙mol⁻¹; ∆S˚, 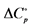, J∙K⁻¹∙mol⁻¹.

increase of the acidic strength for the protonated nitrogen group. It is worthwhile to mention that as the number of -CH₂OH group becomes greater, the enhancement of the acidity decreases as in the case of (GLYCINE) [1] , (BICINE) [3] and (TRICINE) [2] . This trend is consistent for ADA (present study in Table 4). According to Timimi and Everett [17] [18] , in addition to decrease in the value of pK₂, values of ∆H˚ should decrease with corresponding increase of −∆S˚ and. From Table 4 at 298.15 K, for (GLYCINE) [1] the value of ∆H˚ = 44,141 J∙mol⁻¹, ∆S˚ = −39.3 J∙K⁻¹∙mol⁻¹, and = −50 J∙K⁻¹∙mol⁻¹ whereas for ADA, ∆H˚ = 12,252 J∙mol⁻¹, ∆S˚ = −89.9 J∙K⁻¹∙mol⁻¹ and = −148 J∙K⁻¹∙mol⁻¹. It is clear from Table 4 that the trend based on the interpretation of Timimi and Everett [17] [18] , is observed in this study. The difference in the values of ∆S˚ and between GLYCINE and ADA is significant. The more negative values of ∆S˚ indicate that electrostatic interactions of charged species such as ADA^±−, H⁺ and ADA⁻² with solvent water molecules will increase the amount of order in the proximity of those charges. The explanation is that the charge type appears to be the primary factor in determining the magnitude of the large negative values of [19] . There is some evidence that the non-electrostatic effects involving changes in water structure often play a significant role. To the author’s knowledge, no data for the thermodynamic functions for ADA using Ag-AgCl electrodes are available in the literature.

6. Conclusion

The precise emf method yields very stable, accurate, and reliable data with accuracy better than 0.04 mV in the entire temperature range. The uncertainty in the values of pK₂ from Equation (5) falls within 0.0004. At 298.15 K and 310.15 K (body temperature) the pK₂ values are 6.879 and 6.764, respectively. Thus the buffer solution of NaADA + Na₂ADA would be useful for the measurement of pH in biological specimens. These pH data are needed by scientist for biomedical research and would formulate a database for pH standard reference “blood buffer”. In a separate communication of pH, results of several buffer solutions of NaADA and Na₂ADA will be reported as was published for the zwitterionic buffer (ACES) [20] [21] .

Acknowledgements

The authors are grateful for the funding from the National Institutes of Health (NIH-AREA) under the grant 2R15GM66866-3. The content of this paper is the sole responsibility of the authors and does not necessarily represent the official views of the NIH of the National Institutes of the General Medical Science. Rabindra N. Roy is indebted to the Hoffman Endowment Research Fund.

References

NOTES

^*Corresponding author.