Open Journal of Physical Chemistry
Vol. 2 No. 3 (2012) , Article ID: 22118 , 6 pages DOI:10.4236/ojpc.2012.23023
Conformational and Bonding Analysis of C2H42+
Department of Chemistry, Islamic Azad University of Abadeh, Abadeh, Iran
Email: shafiee@iaug.ac.ir
Received March 6, 2012; revised April 7, 2012; accepted May 10, 2012
Keywords: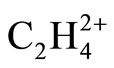 ; LCP; Hyperconjugation; QTAIM; Pauli Exclusion Principle
; LCP; Hyperconjugation; QTAIM; Pauli Exclusion Principle
ABSTRACT
In this report, different models of bonding and structure such as Lewis, VSEPR, Ligand close packing (LCP), VB, qualitative MO and QTAIM have been applied to analyze the Bonds and structures of two equilibrium geometries (planar D2h and perpendicular D2d) of 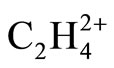 . The geometries were optimized at near RHF and MP2 limit using ccpVTZ basis set. While the above bonding models are successfully applied for predicting the low energy isomers of molecules, prior to solving the Schrödinger equation, it is shown that the cited models fail in predicting the existence of perpendicular, D2d form of
. The geometries were optimized at near RHF and MP2 limit using ccpVTZ basis set. While the above bonding models are successfully applied for predicting the low energy isomers of molecules, prior to solving the Schrödinger equation, it is shown that the cited models fail in predicting the existence of perpendicular, D2d form of 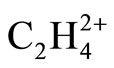 . In this regard the interpretations of significant energetic stabilization of D2d form over planar isomer has also been revisited. This is attributed to the hidden effect of the Pauli Exclusion principle.
. In this regard the interpretations of significant energetic stabilization of D2d form over planar isomer has also been revisited. This is attributed to the hidden effect of the Pauli Exclusion principle.
1. Introduction
The earliest work on the potential energy surface (PES) of 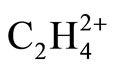 has shown the existence of twisted (D2d)
has shown the existence of twisted (D2d)  minimum and planar (D2h) transition state geometries [1]. The remarkably large rotational barrier energy, 28.1 kcal/mol has been described by the Hyperconjugation between two formally vacant orbitals and corresponding vicinal CH2 group [1]. The substituted ethylene dications have also been extensively studied [2,3] and the results were explained using descriptive tools such as π donation/conjugation, orbital diagrams, lone pairs, steric repulsion and Hyperconjugation. The energy lowering in twisted geometry of ethylene radical cation [4,5] has also been described by the attractive interaction of a p orbital of C atom with the p-like group orbital of adjacent σ bonds [6,7]. We believe that the proposed explanations about the energy lowering in twisted geometry of
minimum and planar (D2h) transition state geometries [1]. The remarkably large rotational barrier energy, 28.1 kcal/mol has been described by the Hyperconjugation between two formally vacant orbitals and corresponding vicinal CH2 group [1]. The substituted ethylene dications have also been extensively studied [2,3] and the results were explained using descriptive tools such as π donation/conjugation, orbital diagrams, lone pairs, steric repulsion and Hyperconjugation. The energy lowering in twisted geometry of ethylene radical cation [4,5] has also been described by the attractive interaction of a p orbital of C atom with the p-like group orbital of adjacent σ bonds [6,7]. We believe that the proposed explanations about the energy lowering in twisted geometry of 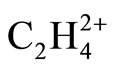 are based on the mixed effects of overlapping, charge separation, Hyperconjugation models. It is the goal of this work to reinvestigate the effect of each of these models on the final geometry of
are based on the mixed effects of overlapping, charge separation, Hyperconjugation models. It is the goal of this work to reinvestigate the effect of each of these models on the final geometry of 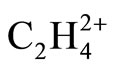 individually. In this work the previous computations with small size Pople type basis sets [1,2] have been extended to larger correlation-consistent basis sets.
individually. In this work the previous computations with small size Pople type basis sets [1,2] have been extended to larger correlation-consistent basis sets.
2. Computational Details
Ab initio computations were performed at both RHF and MP2 methods using cc-pVTZ basis set [8]. PC GAMESS 7.1.5 package [9] running on parallel mode on 5 PCs cluster was used for optimization and frequency calculations. The total electron densities (Rho functions) constructed from wave functions were analyzed, using AIM2000 and MORPHY99 softwares [10-13]. The useful utilities implemented in the ChemCraft program [14] were optimized for handling the outputs of PC GAMESS.
3. Results and Discussion
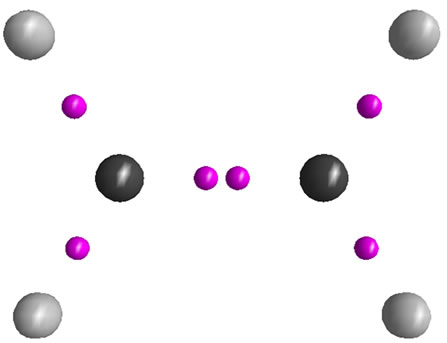
The resulted ab initio geometries and energies of C2H4 and 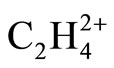 are gathered in Figure 1. Some differences between the results of present computations at MP2 level and those of 6-31G* and 6-31G** [1,2] are discussed first. C-C distances which have been reported previously as 1.317 and 1.587 Å in C2H4 and
are gathered in Figure 1. Some differences between the results of present computations at MP2 level and those of 6-31G* and 6-31G** [1,2] are discussed first. C-C distances which have been reported previously as 1.317 and 1.587 Å in C2H4 and  (D2h) respectively [1], are 1.332 and 1.603 Å, each are 0.015 Å longer at MP2 level. In contrast, the C-C distance in
(D2h) respectively [1], are 1.332 and 1.603 Å, each are 0.015 Å longer at MP2 level. In contrast, the C-C distance in 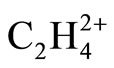 (D2d) shrinks from 1.432 [1] to 1.393 Å, the significant shortening of 0.039 Å. The difference between C-C distances between two
(D2d) shrinks from 1.432 [1] to 1.393 Å, the significant shortening of 0.039 Å. The difference between C-C distances between two  isomers is reported as 0.21 Å, 0.055 Å longer than previously computed value, i.e. 0.155 Å [1]. The energy difference between two isomers is reported as 30.9 kcal/mol at MP2 level, in agreement with previously reported value of 28.1 kcal/mol [1,2]. As depicted in Figure 1, two major geometrical changes occur from D2h to D2d form.
isomers is reported as 0.21 Å, 0.055 Å longer than previously computed value, i.e. 0.155 Å [1]. The energy difference between two isomers is reported as 30.9 kcal/mol at MP2 level, in agreement with previously reported value of 28.1 kcal/mol [1,2]. As depicted in Figure 1, two major geometrical changes occur from D2h to D2d form.
1) The perpendicular arrangement of Hydrogen atoms in D2d form
2) The significant shortening of C-C distances in D2d C-H distances are almost equal between two 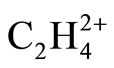 isomers.
isomers.
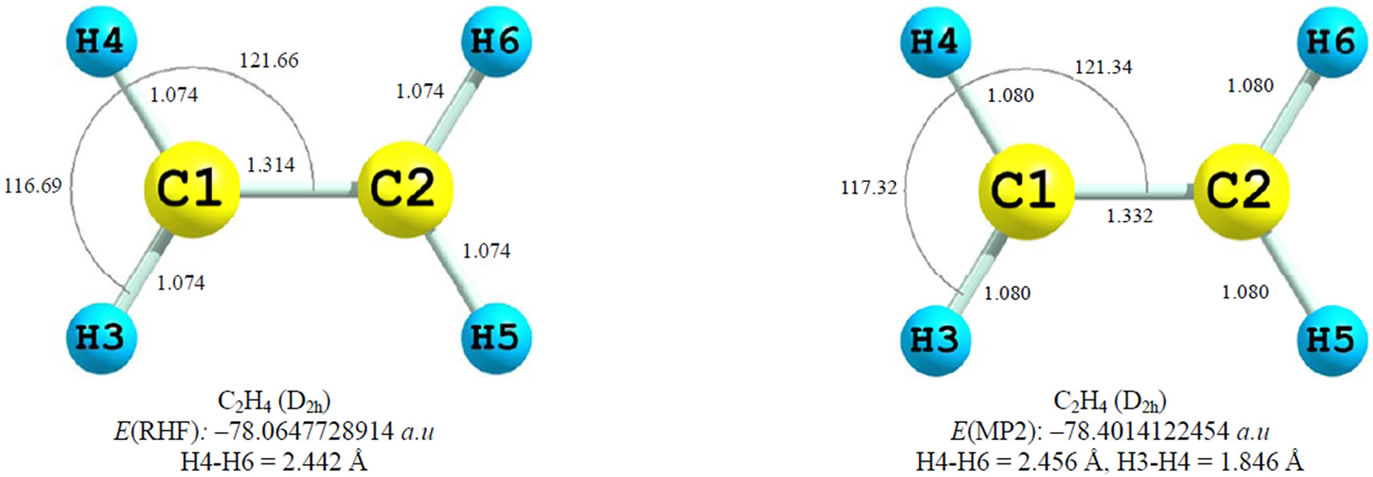

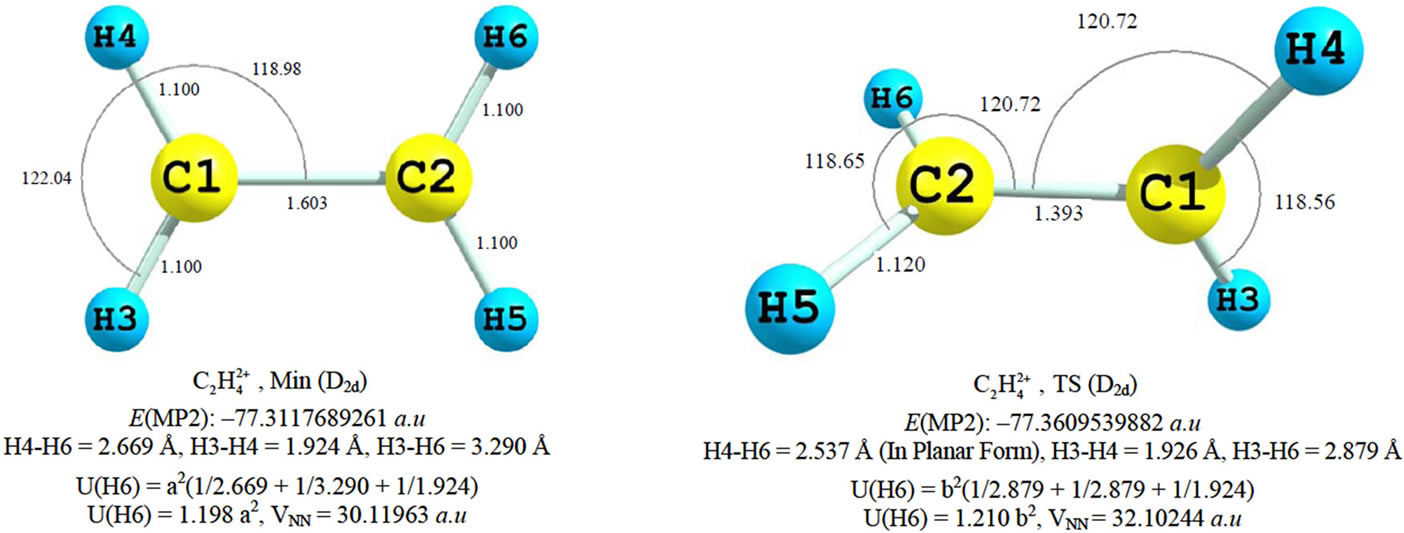
Figure 1. Geomertical parameters, total energie, germinal and vicinal HH distances in C2H4 and 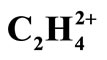 at RHF/cc-pVTZ and MP2(FC)/cc-pVTZ models. “TS” stands for transition state and “Min” stands for local minimum geometry on PES. U is the electrostatic repulsive potential energy. (a) and (b) are the charges of H atoms in two molecules.
at RHF/cc-pVTZ and MP2(FC)/cc-pVTZ models. “TS” stands for transition state and “Min” stands for local minimum geometry on PES. U is the electrostatic repulsive potential energy. (a) and (b) are the charges of H atoms in two molecules.
How different chemical models predict or provide the explanation about these geometrical changes is discussed below. Here we start with basic Lewis model.
3.1. Lewis Model
In Lewis model, a planar structure composed of single bonds for 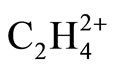 can be written [15]. The formal charge of each C is +1 and that of H is zero. Simple electrostatic rule predicts that the C-C distances in planar Lewis structure should be longer than 1.5 Å, the normal C-C single bond in saturated hydrocarbons, because of the repulsion between two C atoms; each bears a positive formal charge. In this model the existence of more stable perpendicular form cannot be predicted or described.
can be written [15]. The formal charge of each C is +1 and that of H is zero. Simple electrostatic rule predicts that the C-C distances in planar Lewis structure should be longer than 1.5 Å, the normal C-C single bond in saturated hydrocarbons, because of the repulsion between two C atoms; each bears a positive formal charge. In this model the existence of more stable perpendicular form cannot be predicted or described.
3.2. VSEPR
The VSEPR model predicts that the three single bonding pairs around each C atom should adapt the trigonal arrangement and thus the molecular geometry could be planar [15,16]. However the model is only reliable for predicting the relative geometry around any one central atom and not the relative arrangements of the bonds around two adjacent atoms [16]. Usually the bond-pair bond-pair repulsion and Ligand-Ligand interaction (steric repulsion) effects are added to VSEPR to account for geometrical changes. The internuclear distances depicted in Figure 1, show that the vicinal CH bonds repulsion in planar isomer is less than twisted, since they are separated from each other by longer C-C distances. Figure 1 indicates that in both  isomers the vecinal HH distances are significantly longer than 2.40 Å (sum of the Van der Waals radia) so steric repulsion between them is negligible and therefore is not responsible for twisting the geometry to D2d form. Therefore VSEPR together with steric repulsion model cannot predict or explain the existence of twisted
isomers the vecinal HH distances are significantly longer than 2.40 Å (sum of the Van der Waals radia) so steric repulsion between them is negligible and therefore is not responsible for twisting the geometry to D2d form. Therefore VSEPR together with steric repulsion model cannot predict or explain the existence of twisted  .
.
3.3. Ligand Close-Paking
Empirical Ligand close-packing (LCP) model which is the extension of VSEPR [16], treats ligands as hard sphere objects packed around central atom, i.e., C atom. “Each ligand can be considered to be touching its neighbors and can be assigned a nonbonded radious, which is given by the half the ligand-ligand distance” [16]. The 1,3 nonbonded radius of H atom is 0.92 Å [16]. For example the MP2 geometry of ethylene shows a near perfect close-packing of two H atoms and one CH2 group around each C atom, since C-C distance is 1.339 and germinal HH distance is 1.846 Å (twice that of their 1,3 nonbonded radius). No steric repulsion exists between two vicinal H atoms too. Close inspection of MP2 geometries of  , Figure 1, reveals that the internuclear distances in perpendicular
, Figure 1, reveals that the internuclear distances in perpendicular 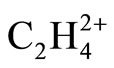 is approximately consistent with the LCP model. H3-H4 distance is 1.926 Å and C-C is 1.393 Å. The observed lengthening of Ligand-Ligand distances, in comparison to ethylene, can be assigned to the electrostatic repulsion between positively charged ligands. Still the preferred D2d isomer of
is approximately consistent with the LCP model. H3-H4 distance is 1.926 Å and C-C is 1.393 Å. The observed lengthening of Ligand-Ligand distances, in comparison to ethylene, can be assigned to the electrostatic repulsion between positively charged ligands. Still the preferred D2d isomer of 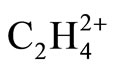 obtained at MP2 level can not be predicted by LCP model.
obtained at MP2 level can not be predicted by LCP model.
3.4. VB, Hyperconjugation and Steric Repulsion
The bond angles about 120.0° around C nuclei, Figure 1, in both forms are consistent with the SP2 hybridization in VB model. Assuming that each C atoms loses one electron, the valence atomic orbitals in C+ with the electronic configuration as 1s2 2s2 2p1, could participate in hybridization process and produce three SP2 orbitals to overlap with 1s orbitals of H atoms and SP2 orbital of adjacent Carbon. The existence of twisted isomer is explained by adding hyperconjugation concept to VB. While VB tends to localize electrons between the nuclei, the hyperconjugation tends to delocalize them. The vacant p orbitals, one on each C atom, interact with corresponding vicinal σ bonds in CH2 [1,6] and therefore lowers the molecular energy. According to our MP2 results this effect (hyperconjugation) should be abnormally strong if it solely responsible for significant lowering in energy (30 kcal/mol) of D2d isomer and corresponding geometrical changes (0.21 Å C-C shortening). This is surprising since the hyperconjugation is a weak effect.
We examined the strength of steric effect which was used to account for the perpendicular arrangement of positively charged Hydrogen atoms [1]. Simple calculation of the electrostatic repulsion energy (U) for each H atom (assuming them as point charges) has been done on MP2 geometries, Figure 1. The results demonstrate that if each H atom bears more positive charges on D2d isomer, then each H atom will suffer greater repulsion in comparison to D2h form. If the H atoms bear same charge in two isomers, then D2d form will again suffer from greater repulsion between hydrogen atoms, or at least the same as D2h. In agreement with our simple analysis the VNN (nuclear-nuclear potential energy) value is also greater in D2d form at MP2 level, Figure 1.
It is concluded that the energetic and geometric changes cannot be explained based on the weak hyperconjugation or even reduction of steric repulsion between H atoms in D2d isomers.
3.5. Qualitative MO
Analyzing the orbital density [7,17] is other method for tracking the geometrical changes. The densities, of HOMO and HOMO-1 for each isomer of  are depicted in Figure 2. The shape of MOs in D2h form support the VB picture of bonding. The HOMO and HOMO-1 of D2d are degenerate and they are more delocalized than HOMO of D2h. Non of the MOs in D2d show the orbital density between C nuclei, the density which is necessary for accounting the significant shortening of C-C distances in this isomer. More inspection revealed that The HOMO-2 of the D2d shows orbital density between C nuclei. HOMO-2 shape of D2d is the same in shape to HOMO-1 in D2h.
are depicted in Figure 2. The shape of MOs in D2h form support the VB picture of bonding. The HOMO and HOMO-1 of D2d are degenerate and they are more delocalized than HOMO of D2h. Non of the MOs in D2d show the orbital density between C nuclei, the density which is necessary for accounting the significant shortening of C-C distances in this isomer. More inspection revealed that The HOMO-2 of the D2d shows orbital density between C nuclei. HOMO-2 shape of D2d is the same in shape to HOMO-1 in D2h.
Again we did not find any reasonable explanations for the two major geometrical changes which we mentioned earlier in this work. We suggest that more sophisticated orbital analysis such as Walsh diagrams [18] can be applied to predict the lowest isomer of  .
.
3.6. The QTAIM
In the framework of QTAIM theory, the total molecular electron density, Rho(ρ) [19], is the source of chemical information about the molecule. The integration of Rho over all space is exactly equal to the total number of electrons in the molecule [7,19].

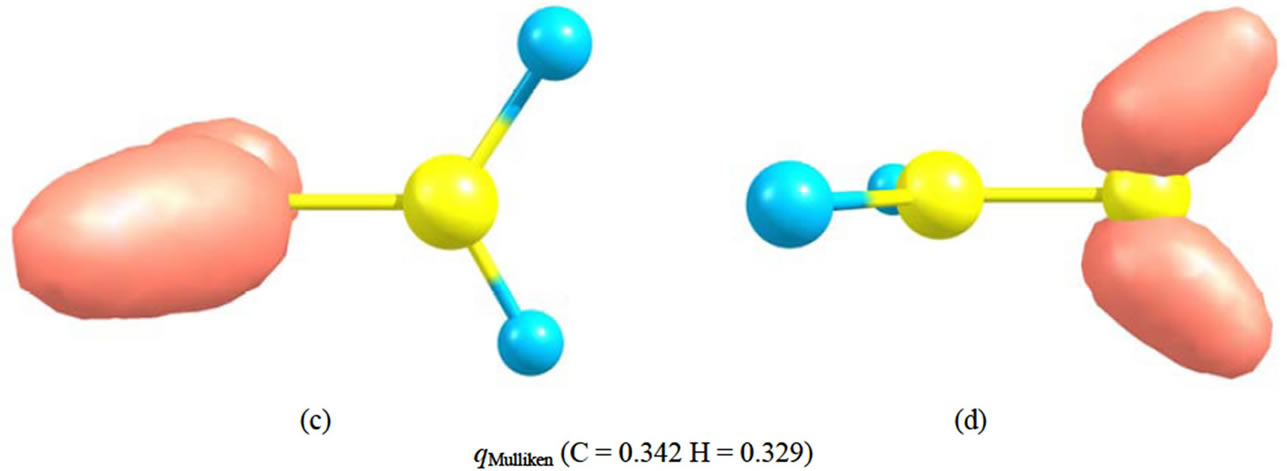
Figure 2. The RHF orbital density (Ψ2MO) of the HOMO (a, c), HOMO-1 (b, d) and Mulliken atomic charges in planar (a, b) and perpendicular (c, d) forms of .
.
We skip the normal topological analysis of electron density at this stage and continue the discussion using the Rho(ρ) values at the geometric midpoint between C-C and C-H in two cited isomers of  .
.
At MP2 level the ρ values at the chosen points in D2h are 0.232, 0.345 a.u., in D2d are 0.343, 0.316 a.u. respectively. These numbers nicely represent the correct picture of distribution of electronic charge from C-H regions to C-C region when the geometry is changed from D2h to D2d.The accumulation of charge density between C nuclei in twisted form, result in the decrease of positive charge on C atoms and the marked decrease of C-C length [20]. Because of this transferring of negative charge, the H atoms bear more positive charge in D2d. While the ρ between C-C changes by 0.111 a.u. from D2h to D2d, the corresponding value in each CH region is only 0.029 a.u. This explains why C-H distances remain almost the unchanged between two isomers.
Does the ρ provide the explanation for why the D2d isomer is the lowest energy isomer? The quantum theory of atoms in molecules has provided the physical basis for the LCP and VSEPR models based on the arrangement of maxima in the Lapalcian map of ρ around the central atom [21]. Instead of electron pairs, the concept of electron domains is used when using LCP or VSEPR in their new forms [15]. It is expected that at least three maxima be found around each C atom. The maps of Laplacian of electron density for C2H4 and  geometries are depicted in Figure 3. The number and the orientation of the maxima around C atoms are the same, 3 maxima in trigonal orientation in all cases, Figures 3(a1)-(c1). The number of domains of charge concentration are also the same, Figures 3(a3)-(c3). The comparison of contour maps of Laplacian among C2H4 and two isomers of
geometries are depicted in Figure 3. The number and the orientation of the maxima around C atoms are the same, 3 maxima in trigonal orientation in all cases, Figures 3(a1)-(c1). The number of domains of charge concentration are also the same, Figures 3(a3)-(c3). The comparison of contour maps of Laplacian among C2H4 and two isomers of  , Figures 3(a)-(c) show the existence of distinct regions of charge accumulation between C nuclei in C2H4. In both
, Figures 3(a)-(c) show the existence of distinct regions of charge accumulation between C nuclei in C2H4. In both  isomers this region disappears. This is due to the removal of two electrons from the parent molecule (C2H4). The Laplacian maps of the two
isomers this region disappears. This is due to the removal of two electrons from the parent molecule (C2H4). The Laplacian maps of the two  isomers are essentially the same. It is not clear yet why
isomers are essentially the same. It is not clear yet why  preferred geometry is the D2d isomer.
preferred geometry is the D2d isomer.
Finally we present the full QTAIM analysis [15,19-20, 22], Atomic basin charge and energy values in Table 1. The trends of basin charges are the same as what has been predicted by the ρ values at the midpoints of CH and C-Cs. The positive charge of each C basin in D2d is half of the value in D2h. The comparison of atomic charges (Table 1) indicates that 0.05 unit of charge is transferred from each H basin to C basins when the geometry is changed from D2h to D2d. The volumes of C basins increase and those of H basins decrease by this charge transfer. Energy analysis demonstrates that each C basin is stabilized by 68.15 kcal/mol but each H basin is destabilized by 26.36 kcal/mol, from D2h to D2d form.
 (a1)
(a1)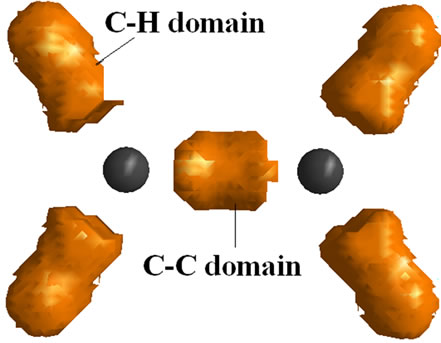 (a2)
(a2)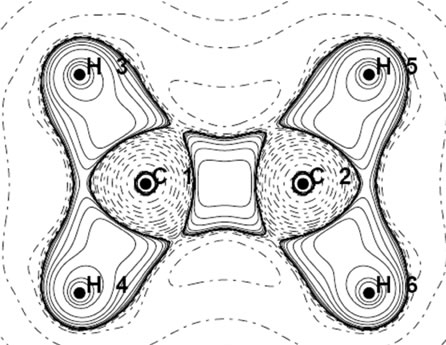 (a3)
(a3) (b1)
(b1) (b2)
(b2)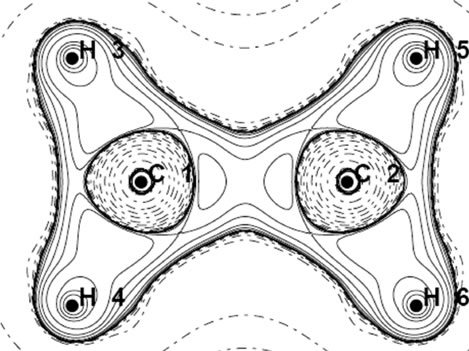 (b3)
(b3)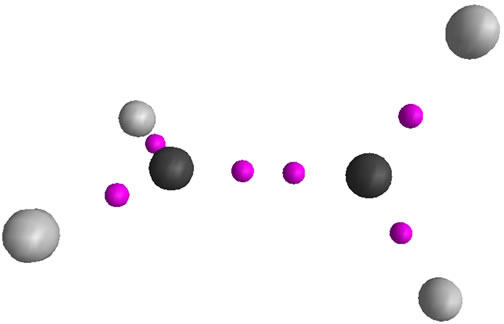 (c1)
(c1) (c2)
(c2) (c3)
(c3)
Figure 3. Laplacian maps of C2H4 (a), 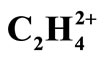 planar (b),
planar (b), 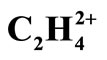 perpendicular (c) at MP2/cc-pVTZ level.Maximum points (small circles) on Laplacian of Rho, (a1)-(c1). 3D pictures of isosurfaces), –0.1 a.u, of charge concentration i.e. negative value of Laplacian, (a2)-(c2). Contour plots of Laplacian maps (dash lines = charge depletion, solid line = charge concentration), (a3)-(c3).
perpendicular (c) at MP2/cc-pVTZ level.Maximum points (small circles) on Laplacian of Rho, (a1)-(c1). 3D pictures of isosurfaces), –0.1 a.u, of charge concentration i.e. negative value of Laplacian, (a2)-(c2). Contour plots of Laplacian maps (dash lines = charge depletion, solid line = charge concentration), (a3)-(c3).

Table 1. Atomic properties (in atomic units) from QTAIM analysis at MP2/cc-pVTZ.
4. Conclusion
In 1954 Lennard-Jones published the paper, the distribution functions of neutral fermionic particles with same spin moving in the closed ring and Surface of sphere [23]. The orientation of maxima of probability of finding the particles on the ring or sphere, were demonstrated mathematically as 180˚ for two particles, 120˚ for three particles and tetrahedral arrangement for four particles moving on the surface of sphere. The paper has been written to show the net effect of PEP in distributing the electrons in confined region of space. Adding the presented discussion (Failure of different models) it seems that the molecular geometry is controlled by hidden effect of Pauli Exclusion Principle, PEP [21] which is imposed to the wave function.
REFERENCES
- K. Lammertsma, M. Barazaghi, G. A. Olah, J. A. Pople, A. J. Kos and P. V. R. Schleyer, “Carbodications. 6. The Ethylene Dication: A Theoretical Study of the Ethylene Dication (C2H42+) Potential-Energy Surface,” Journal of the American Chemistry Society, Vol. 105, No. 16, 1983, pp. 5252-5257. doi:10.1021/ja00354a012
- G. Frenking, “Substituted Ethylene Dications: Planar or Perpendicular?” Journal of the American Chemistry Society, Vol. 113, No. 7, 1991, pp. 2476-2481. doi:10.1021/ja00007a020
- T. Ohwada and K. Shudo, “Substituted Ethylene Dications. Structures of Phenylmethyl Cations Substituted with an Electron-Withdrawing Group on the Cation Center,” Journal of the American Chemistry Society, Vol. 111, No. 1, 1989, pp. 34-40. doi:10.1021/ja00183a006
- L. A. Eriksson, S. Lunell and R. J. Boyd, “Electronic Structure Calculations of Hydrocarbon Radical Cations: A Density Functional Study,” Journal of the American Chemistry Society, Vol. 115, No. 15, 1993, pp. 6896-6900. doi:10.1021/ja00068a055
- M. L. Abrams, E. F. Valeev, C. D. Sherrill and T. D. Crawford, “The Equilibrium Geometry, Harmonic Vibrational Frequencies, and Estimated ab Initio Limit for the Barrier to Planarity of the Ethylene Radical Cation,” Journal of Physical Chemistry A, Vol. 106, No. 11, 2002, pp. 2671-2675. doi:10.1021/jp0134143
- R. V. I. Rauk, “Orbital Interaction Theory of Organic Chemistry,” Wiley Inter-Science, New York, 2001.
- C. J. Cramer, “Essentials of Computational Chemistry Theories and Models,” Wiley, New York, 2008.
- T. H. Dunning Jr., “Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen,” Journal of Chemical Physics, Vol. 90, No. 2, 1989, pp. 1007-1023. doi:10.1063/1.456153
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, “General Atomic and Molecular Electronic Structure System,” Journal of Computational Chemistry, Vol. 14, 1993, pp. 1347-1363.
- F. Biegler-König, “Calculation of Atomic Integration Data,” Journal of Computational Chemistry, Vol. 21, No. 12, 2000, pp. 1040-1048. doi:10.1002/1096-987X(200009)21:12<1040::AID-JCC2>3.0.CO;2-8
- F. Biegler-König, J. Schönbohm and D. Bayles, “AIM 2000—A Program to Analyze and Visualize Atoms in Molecules,” Journal of Computational Chemistry, Vol. 22, 2001, pp. 545-559.
- P. L. A. Popelier and R. G. A. Bone, “MORPHY99,” A Topological Analysis Program, UMIST, Engl, EU.
- P. L. A. Popelier, “MORPHY, a Program for an Automated ‘Atoms in Molecules’ Analysis,” Computer Physics Communications, Vol. 93, No. 2-3, 1996, pp. 212-240. doi:10.1016/0010-4655(95)00113-1
- G. A. Zhurko and D. A. Zhurko, “ChemCraft, Tool for Treatment of the Chemical Data.” http://www.chemcraftprog.com
- P. L. A. popelier and R. J. Gillespie, “Chemical Bonding and Molecular Geomerty from Lewis to Electron Dnsities,” Oxford University Press, Oxford, 2001.
- R. J. Gillespie and I. Hargittai, “The VSEPR Model of Geometry,” Allyn & Bacon, Boston, 1991.
- D. A. McQuarrie, “Quantum Chemistry,” Oxford University Press, Oxford, 1983.
- B. Gimarc, “Application of Qualitative Molecular Orbital Theory,” Accounts of Chemical Research, Vol. 7, No. 11, 1974, pp. 384-392. doi:10.1021/ar50083a004
- R. F. W. Bader, “Atoms in Molecules: A Quantum Theory,” Clarendon Press, Oxford, 1990.
- R. F. W. Bader, “Chem 106 Seminar #2,” Case Western Reserve University, 2008.
- R. F. W. Bader, R. J. Gillespie and P. J. MacDougall, “A Physical Basis for the VSEPR Model of Molecular Geometry,” Journal of the American Chemistry Society, Vol. 110, No. 22, 1988, pp. 7329-7336. doi:10.1021/ja00230a009
- P. L. A. Poplier, “Atoms in Molecules: An Introductory,” Prentice Hall, Upper Saddle River, 2000.
- S. J. Lennard-Jones, “New Ideas in Chemistry,” Advanced Science, Vol. 11, No. 54, 1954, p. 136.

