Open Journal of Physical Chemistry
Vol. 2 No. 2 (2012) , Article ID: 19167 , 6 pages DOI:10.4236/ojpc.2012.22016
Sensitivity of the C-N Vibration to Solvation in Dicyanobenzenes: A DFT Study
Department of Biology, Chemistry and Environmental Health Science Benedict College, Columbia, USA
Email: *qinc@benedict.edu
Received January 12, 2012; revised March 20, 2012; accepted April 23, 2012
Keywords: Dicyanobenzene; Vibration; Solvation; Infrared Spectrum; Density Functional Theory
ABSTRACT
Using DFT calculations, we have studied the C-N vibration of dicyanobenzenes in different solvents. The effects of solvent polarity and hydrogen bonding were evaluated. The frequency is decreased by 4 cm–1 when the solvent polarity increases. In the current study, the red shift due to the solvent polarity was underestimated by PCM. For hydrogen bonding, the frequency is increased by 10 cm–1 because of the charge transfer from the lone pair of nitrogen in C≡N to water, which slightly increases the bond strength of C-N. The C-N vibration of dicyanobenzenes is calculated to be sensitive to solvation.
1. Introduction
The vibration of the cyano group (C≡N) in organic and biological molecules has been studied as infrared (IR) probe of local environment in biological systems [1-11]. Previous studies show that the C-N vibration is highly localized, causes only negligible perturbation to the local three-dimensional structure, and the frequency is also very sensitive to the environmental change [12]. All of those make it an ideal probe for the local biological environment such as electrostatic potential, dielectric constant, ionic strength, and hydrogen bonding.
To predict the local environment of a targeted domain, one or more cyano groups have to be inserted into the biomolecule. The IR spectrum will then be taken and analyzed. Based on the frequency shift, peak width and intensity change of the C-N stretching, the local environment can be predicted. Therefore, a molecular level understanding of the frequency shift, peak width and intensity change caused by various local environmental conditions is of increasing importance and will significantly advance the predictive capabilities. Nowadays, theoreticcal modeling has advanced to a point where vibrations inside of a molecule can be examined at a level of quantum theory [13-17]. Furthermore, the solvation effects can be evaluated by using the Polarizable Continuum Model (PCM) [18] and also by including explicit solvent molecules in the quantum model.
Previous studies have shown that a single cyano group can provide predictive information about the local environment in biological systems, but there are still uncertainties in predictions since the inner cancellation between different environmental factors is not considered. For example, the C-N stretching frequency decreases with the dielectric constant of the solvent, but increases very quickly if hydrogen bonding occurs, which makes the prediction very difficult [1,2,19]. Recently, Krummel and Zanni have shown that the coupling between two cyano groups is detectable within a distance of even more than 4.5 Å and is very promising in monitoring DNA structures with a Fourier Transform Infared (FTIR) [20]. This has opened a door to development of new dicyano probes with higher accuracy since the coupling between the two cyano groups will possibly provide additional information about the local environment and will in turn improve the prediction. In the present study, the sensitivity of the C-N vibration to solvation in three isomers of dicyanobenzene was examined using Density Functional Theory (DFT) methods.
2. Theory and Method
The ground-state geometries of 1,2-dicyanobenzene (o-DCB), 1,3-dicyanobenzene (m-DCB) and 1,4-dicyanobenzene (p-DCB) were optimized using the Generalized Gradient Approximation (GGA) hybrid functional of B3LYP [21,22] in combination with the basis set of 6-31G(d, p) [23-25]. B3LYP has been proven to be very reliable in treating electronic exchange and correlation in small organic molecules. All calculations were performed by Gaussian09 [26] suite of quantum programs. The solvation effects were basically evaluated using the Polarizable Continuum Model (IEFPCM) [18], while explicit solvent molecules were included in the corresponding quantum model where hydrogen bonding occurs. The vibrational frequencies were calculated from analytic second derivatives using a harmonic oscillator model. In addition, the infrared (IR) intensities were calculated from the transition matrix elements of the dipole moment between the initial and final vibrational states.
3. Results and Discussion
3.1. Geometries, Relative Energies, Dipole Moments, Vibrational Frequencies and IR Intensities in the Gas Phase
The structures of dicyanobenzenes are optimized in the gas phase at the B3LYP/6-31G (d, p) level and displayed in Figure 1. Selected bond distances, dipole moments and relative energies are listed in Table 1. It is found that p-DCB is more stable than m-DCB and o-DCB with a lower energy of 0.38 kcal/mol and 2.01 kcal/mol, respecttively. Obviously, larger separation between two cyano groups leads to less steric repulsion and lower the total energy from o-DCB, m-DCB to p-DCB. Correspondingly, the dipole moment of each molecule decreases in the same order, which is largely determined by the relative position of the two cyano groups. In p-DCB, the two groups are aligned linearly, but in opposite directions, which leads to a zero polarity. However, they are nearly parallel and in the same direction in o-DCB, which gives the largest dipole moment of 7.08 Debye. Between pDCB and o-DCB is m-DCB with a dipole moment of 4.27 Debye.
For the selected bond distances in Table 1, the calculated values are slightly larger than those form x-ray diffraction, but within 0.04 Å and have shown a fairly good agreement. Since all calculations here are based on single molecules in the gas phase only, no intermolecular interactions are considered, which is different from the x-ray experiment [27,28]. It is notable that the C-C bonds on the benzene ring close to the cyano groups are elongated compared to those further away. For example, C1-C2 and C2-C3 are longer than C3-C4 and C4-C5 in o-DCB. Electron population analysis gives the Mulliken charge of C1, C3, C7 and N8 in o-DCB as +0.140e, –0.053e, +0.236e and –0.462e, respectively. Significant negative charge of 0.226e is detected on C≡N, compared to a calculated value of 0.128e for acetonitrile. The high electronegativity of nitrogen has led to a charge transfer from benzene to C≡N, which should destablize the ring structure and make the neighboring bonds slightly longer. The electron density is finally injected into the lowest unoccupied molecular orbital (LUMO) of C≡N. Since the LUMO is of antibonding character, this electron trans fer makes the C-N bond slightly longer than in acetonitrile, which has a calculated C-N bond distance of 1.160 Å at the same level of theory. In addition, the π-conjugation in benzene and C≡N is merged and extended to the whole molecule, which brings partial π-bonding character to C1-C7 and makes the bond (~1.43 Å) significantly shorter than a C-C single bond (~1.50 Å). Very similar results were observed for m-DCB and p-DCB as well.
Since the C-N vibrations are highly localized and will only be used for the probing in biological systems, only the two C-N vibrational modes, symmetric and asymmetric, will be discussed in this report. In the symmetric
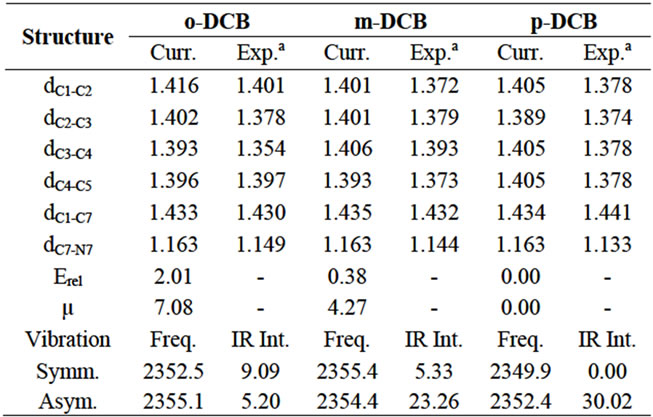
Table 1. Calculated bond distances (Å), relative energies (kcal/mol), dipole moments (Debye), vibrational frequencies (cm–1) and IR intensity (km/mol) for dicyanobenzenes.

Figure 1. Optimized structures of dicyanobenezenes.
mode, both C and N in the two cyano groups move towards or away from each other at the same pace. However, in the asymmetric mode, the two atoms move towards each other in one cyano group, while they move away from each other in the other cyano group. Calculated vibrational frequencies and infrared (IR) intensities in the gas phase are also tabulated in Table 1. For p-DCB, the symmetric mode is not IR active because two C-N vibrations cancel each other and gives no change to the net dipole moment. However, the asymmetric mode has the highest intensity of 30.02 km/mol. For o-DCB, two modes are separated by 2.7 cm–1, indicating a possible detectable long-range vibrational coupling. Also both modes are sensitive to IR. For m-DCB, the two modes are very close with the asymmetric mode of only 1.0 cm–1 lower in energy, but it has a much higher IR intensity. Although the gas phase calculations cannot represent the real vibrational environment, they truly can provide an easy model to understand the C-N vibration in the selected dicyanobenzenes. Furthermore, the treatment of solvation is needed to provide accurate and reliable predictions.
3.2. Vibrations in Different Solvents
In this section, the solvation is treated using PCM, in which the solvents are electric dipoles and hydrogen bonding is not fully taken into account. The molecular structures are same as those optimized in the gas phase, while vibrational frequencies and IR intensities are calculated in different solvents, including tetrachloromethane (CCl4, εr = 2.2), chloroform (CHCl3, εr = 4.8), dichloromethane (CH2Cl2, εr = 8.9), acetone (CH3COCH3, εr = 20.7), acetonitrile (CH3CN, εr = 37.5) and water (H2O, εr = 78.3). In Figure 2, the calculated solvation energy by PCM is plotted as a function of the solvent dielectric constant. It is found that the solvation energy increases with the polarity of solvent. From the gas phase εr = 0.0) to dichloromethane, it is increased by about 6.5 kcal/mol. However, the change is almost negligible from acetone to water, less than 1.0 kcal/mol. From p-DCB, m-DCB to o-DCB, the solvation energy increases slightly with the molecular polarity. In addition, the calculated vibrational frequencies and IR intensities are plotted as a function of the dielectric constant, and are displayed in Figure 3.
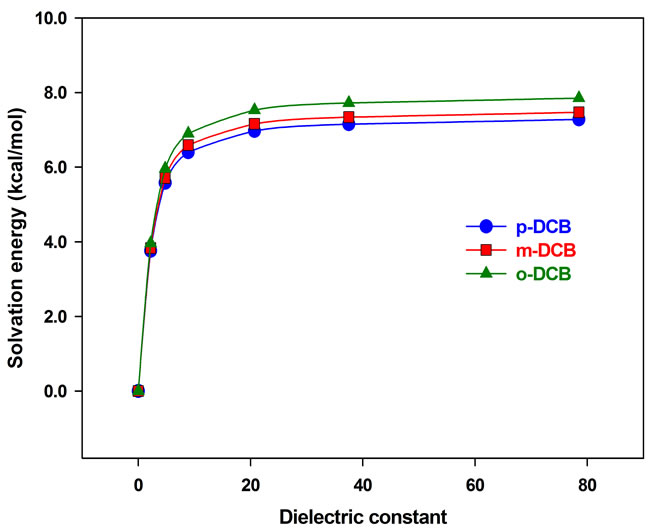
Figure 2. Solvation energy vs dielectric constant.
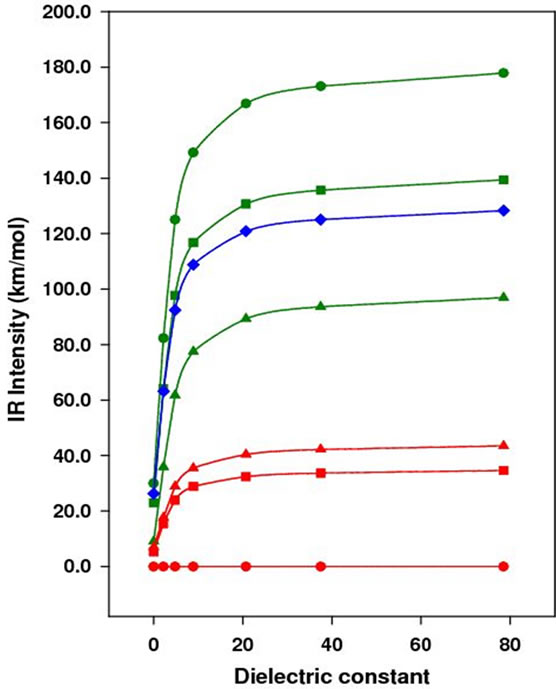
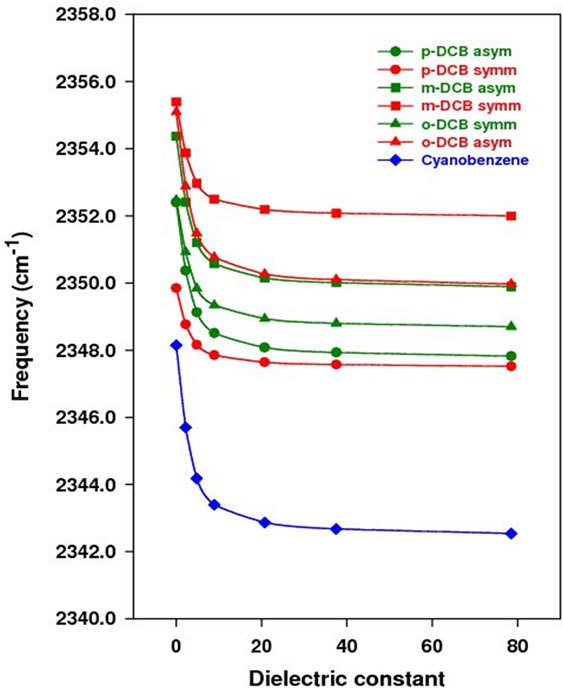
Figure 3. Vibrational frequency (bottom) and IR intensity (top) vs dielectric constant.
In Figure 3, the vibrational frequency of either symmetric or asymmetric mode decreases with the dielectric constant, while the IR intensity increases. From the gas phase to water, the frequency is decreased by 4.0 cm–1 for all except the symmetric mode of p-DCB, which is 2.0 cm–1. To verify the reliability of PCM in predicting shifts of the C-N vibrational frequency in different solvents, the C-N vibrational frequency of acetonitrile is calculated to be 2379.1 cm–1, 2376.6 cm–1, 2375.1 cm–1, and 2374.1 cm–1 at the same level of theory in the gas phase, tetrachloromethane, chloroform, and dichloromethane, respectively. From gas phase to tetrachloromethane, the red shift is 2.5 cm–1, 4.0 cm–1 to chloroform, and 5.0 cm–1 to dichloromethane. The experimental value is 11.5 cm–1, 11.0 cm–1, 12.0 cm–1 in tetrachloromethane, chloroform and methylene chloride, respectively. Obviously, the shift is underestimated by PCM, indicating the importance of including intermolecular interactions in the theoretical model. However, PCM is simple and fast, which provides easiest model to predict the C-N frequency shift. In addition, the C-N vibrational frequency in benzonitrile (BN) is calculated at the same level of theory and shows a decrease of 6.0 cm–1 from gas phase to water, which is larger than the shift calculated for dinitriles in this study.
In an IR probing, the intensity change is also taken into account to provide additional information about the local environment. Figure 3 (right graph) shows the calculated IR intensity as a function of the solvent dielectric constant. With the increase of the solvent polarity, the IR intensity increases dramatically at the beginning. For the asymmetric mode of p-DCB in the gas phase and tetrachloromethane, the intensity changes from 20.0 km/mol to 150.0 km/mol, indicating the highest sensitivity to the solvation. However, the change for benzonitrile is only about 75.0 km/mol from gas phase to tetrachloromethane. In terms of the IR intensity, the theoretical calculations show that p-DCB is more sensitive to the solvent polarity than m-DCB, and o-DCB. Therefore, it is possible to use the IR frequency and intensity change to determine the local bonding structure of the cyano group in biological systems.
3.3. Effects of Hydrogen Bonding
In the PCM model, majorly electrostatic effect is considered. To include the effect of hydrogen bonding, two water molecules were added to each structure and the DCB-water complexes in the gas phase were then opti- mized at the B3LYP/6-31G (d, p) level. For the geometry of benzene ring, no significant changes have been found, while the local H-bonding structure is displayed in Figure 4 with calculated Mulliken charges. In addition, there is no notable difference in the three isomers in terms of

Figure 4. H-Bonding structure of p-DCB-water (Green: p-DCB-water; Purple: p-DCB).
hydrogen bonding, and here only the local structure of p-DCB-water is shown in Figure 4 and discussed in details.
In Figure 4, bond distances and Mulliken charges of p-DCB-Water are displayed in green, while purples for single water and p-DCB. The binding energy is calculated as EDCB-Water-EDCB-EWater and to be 4.5 kcal/mol for all DCB-Water complexes, indicating significant hydrogen bonding between DCB and water. It is found that the hydrogen bonding shortens the C7-N7 bond by 0.002 Å, indicating a slightly stronger C-N bond and higher C-N vibrational frequency. A charge transfer of 0.032e is detected from p-DCB to water. The charge is mainly from the molecular orbital of nitrogen lone pairs. Since the lone pair orbital is of anti-bonding character between C7 and N7, losing electron density should lead to a stronger C-N bond and higher C-N vibrational frequency. The calculated C-N vibrational frequency is 2360.1 cm–1 and 2361.9 cm–1 for the symmetric and asymmetric mode, respectively. The hydrogen bonding of water to p-DCB has increased the C-N vibrational frequency by 10 cm–1. The C-N frequency shift of acetonitrile in dimethyl sulfoxide (DMSO) and water was measured to be 17.5 cm–1 and 6.7 cm–1, respectively [1]. Approximately, we can assume that the effect of the solvent polarity on the C-N vibration is same in the two solvents, and the difference in the C-N vibration is then mainly caused by hydrogen bonding. This effect is calculated to be +10.8 cm–1 and is in an excellent agreement with the value from the current study. In addition, the C-N vibrational frequency of p-DCB-Water is calculated to be 4.0 cm–1 lower in PCM water, which is exactly same as we found for p-DCB in water.
4. Conclusion
We have reported a DFT study of the C-N vibration in dicyanobenzenes (DCB) relevance to the IR probing of local environment in biological systems. The effect of solvent polarity (dielectric constant) and hydrogen bonding were evaluated using PCM and by including two water molecules in the quantum model. The C-N vibrational frequency is decreased by up to 4 cm–1 from the PCM calculations when the solvent polarity increases. However, a large red shift of 17.5 cm–1 was reported for acetonitrile in DMSO [1], which implies that the red shift due to the solvent polarity was underestimated by PCM in the current study. For the hydrogen bonding, the frequency is increased by 10 cm–1 because of the charge transfer from the lone pair of nitrogen to water, which slightly increases the C-N bond strength. The C-N vibration of dicyanobenzenes is calculated to be sensitive to both solvent polarity and hydrogen bonding.
5. Acknowledgements
The authors gratefully acknowledge both the Department of Energy and Department of Defense for financial support of this work (Grant Number: DE-FG52-08NA28800 and W911NF-10-R-006).
REFERENCES
- J. R. Reimers and L. E. Hall, “The Solvation of Acetonitrile,” Journal of the American Chemical Society, Vol. 121, No. 15, 1999, pp. 3730-3744. doi:10.1021/ja983878n
- S. S. Andrews and S. G. Boxer, “Vibrational Stark Effects of Nitriles I. Methods and Experimental Results,” The Journal of Physical Chemistry A, Vol. 104, No. 51, 2000, pp. 11853-11863. doi:10.1021/jp002242r
- I. T. Suydam, C. D. Snow, V. S. Pande and S. G. Box, “Electric Fields at the Active Site of an Enzyme: Direct Comparison of Experiment with Theory,” Science, Vol. 313, No. 5784, 2006, pp. 200-204. doi:10.1126/science.1127159
- Z. Getahun, C. Huang, T. Wang, B. D. Leon, W. F. DeGrado and F. Gai, “Using Nitrile-Derivatized Amino Acids as Infrared Probes of Local Environment,” Journal of the American Chemical Society, Vol. 125, No. 2, 2003, pp. 405-411. doi:10.1021/ja0285262
- M. J. Tucker, Z. Getahun, V. Nanda, W. F. DeGrado and F. Gai, “A New Method for Determining the Local Environment and Orientation of Individual Side Chains of Membrane-Binding Peptides,” Journal of the American Chemical Society, Vol. 126, No. 16, 2004, pp. 5078-5079. doi:10.1021/ja032015d
- M. J. Tucker, R. Oyola and F. Gai, “A Novel Fluorescent Probe for Protein Binding and Folding Studies: p-CyanoPhenylalanine,” Biopolymers, Vol. 83, No. 6, 2006, pp. 571-576. doi:10.1002/bip.20587
- M. M. Waegele, M. J. Tucker and F. Gai, “5-Cyanotryptophan as an Infrared Probe of Local Hydration Status of Proteins,” Chemical Physics Letters, Vol. 478, No. 4-6, 2009, pp. 249-253. doi:10.1016/j.cplett.2009.07.058
- K. C. Schultz, L. Supekova, Y. Ryu, J. Xie, R. Perera and P. G. Schultz, “A Genetically Encoded Infrared Probe,” Journal of the American Chemical Society, Vol. 128, No. 43, 2006, pp. 13984-13985. doi:10.1021/ja0636690
- L. N. Silverman, M. E. Pitzer, P. O. Ankomah, S. G. Boxer and E. E. Fenlon, “Vibrational Stark Effect Probes for Nucleic Acids,” The Journal of Physical Chemistry B, Vol. 111, No. 40, 2007, pp. 11611-11613. doi:10.1021/jp0750912
- M. D. Watson, X. S. Gai, A. T. Gillies, S. H. Brewer and E. E. Fenlon, “A Vibrational Probe for Local Nucleic Acid Environments: 5-Cyano-2′-Deoxyuridine,” The Journal of Physical Chemistry B, Vol. 112, No. 42, 2008, pp. 13188-13192. doi:10.1021/jp8067238
- B. A. Lindquist, D. E. Furse and S. A. Corcelli, “Nitrile Groups as Vibrational Probes of Biomolecular Structure and Dynamics: An Overview,” Physical Chemistry Chemical Physics, Vol. 11, No. 37, 2009, pp. 8119-8132. doi:10.1039/b908588b
- M. G. Maienschein-Cline and C. H. Londergan, “The CN Stretching Band of Aliphatic Thiocyanate Is Sensitive to Solvent Dynamics and Specific Solvation,” The Journal of Physical Chemistry A, Vol. 111, No. 40, 2007, pp. 10020-10025. doi:10.1021/jp0761158
- S. D. Dalosto, J. M. Vanderkooi and K. A. Sharp, “Vibrational Stark Effects on Carbonyl, Nitrile, and Nitrosyl Compounds Including Heme Ligands, CO, CN, and NO, Studied with Density Functional Theory,” The Journal of Physical Chemistry B, Vol. 108, No. 20, 2004, pp. 6450-6457. doi:10.1021/jp0310697
- B. A. Lindquist and S. A. Corcelli, “Nitrile Groups as Vibrational Probes: Calculations of the CN Infrared Absorption Line Shape of Acetonitrile in Water and Tetrahydrofuran,” The Journal of Physical Chemistry B, Vol. 112, No. 20, 2008, pp. 6301-6303. doi:10.1021/jp802039e
- B. A. Lindquist, R. T. Haws and S. A. Corcelli, “Optimized Quantum Mechanics/Molecular Mechanics Strategies for Nitrile Vibrational Probes: Acetonitrile and ParaTolunitrile in Water and Tetrahydrofuran,” The Journal of Physical Chemistry B, Vol. 112, No. 44, 2008, pp. 13991-14001. doi:10.1021/jp804900u
- J. Choi, K. Oh, H. Lee, C. Lee and M. Cho, “Nitrile and thiocyanate IR Probes: Quantum Chemistry Calculation Studies and Multivariate Least-Square Fitting Analysis,” The Journal of Chemical Physics, 128 (2008) 134506. doi:10.1063/1.2844787
- K.-I. Oh, J.-H. Choi, J. Lee, J. Han, H. Lee and M. Cho, “Nitrile and Thiocyanate IR Probes: Molecular Dynamics Simulation Studies,” The Journal of Chemical Physics, Vol. 128, No. 13, 2008, pp. 154504-154511. doi:10.1063/1.2904558
- S. Miertu and J. Tomasi, “Approximate Evaluations of the Electrostatic Free Energy and Internal Energy Changes in Solution Processes,” Chemical Physics, Vol. 65, No. 2, 1982, pp. 239-245. doi:10.1016/0301-0104(82)85072-6
- S. Kaur, E. S. Eberhardt, A. Doucette, A. Chase and C. Dalby, “Solvent Effects on Barrier to Rotation of Enaminonitriles Using Inversion Transfer 1H NMR Spectroscopy and FTIR Spectroscopy,” The Journal of Organic Chemistry, Vol. 67, No. 11, 2002, pp. 3937-3940. doi:10.1021/jo025516a
- A. T. Krummel and M. T. Zanni, “Evidence for Coupling between Nitrile Groups Using DNA Templates: A Promising New Method for Monitoring Structures with Infrared Spectroscopy,” The Journal of Physical Chemistry B, Vol. 112, No. 5, 2008, pp. 1336-1338. doi:10.1021/jp711558a
- C. Lee, W. Yang and R. G. Parr, “Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density,” Physical Review B, Vol. 37, 1988, pp. 785-789. doi:10.1103/PhysRevB.37.785
- A. D. Becke, “Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior,” Physical Review A, Vol. 38, 1988, pp. 3098-3100. doi:10.1103/PhysRevA.38.3098
- V. A. Rassalov, J. A. Pople, M. Ratner and T. L. Windus, “6-31G∗ Basis Set for Atoms K through Zn,” The Journal of Chemical Physics, Vol. 109, 1998, pp. 1223-1229. doi:10.1063/1.476673
- P. C. Harihan and J. A. Pople, “The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies,” Theoretical Chemistry Accounts, Vol. 28, No. 3, 1973, pp. 213-222. doi:10.1007/bf00533485
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFree and J. A. Pople, “Self-Consistent Molecular Orbital Methods. XXIII. A Polarization-Type Basis Set for Second-Row Elements,” The Journal of Chemical Physics, Vol. 77, No. 7, 1982, pp. 3654-3665. doi:10.1063/1.444267
- M. J. Frisch et al., “Gaussian 09, Revision B.01,” Gaussian Inc., Pittsburgh, 2009.
- J. T. López Navarrete, J. J. Quirante, M. A. G. Aranda, V. Hernández and F. J. Ramirez, “Structure, Polarized Micro-Raman and FT-IR Spectra, and AB Initio Calculations of 1,2-Dicyanobenzene,” The Journal of Physical Chemistry, Vol. 97, No. 41, 1993, pp. 10561-10569. doi:10.1021/j100143a009
- J. Janczak and R. Kubiak, “Molecular Structure and Ring Distortions of 1,3-Dicyanobenzene in the Gas Phase and in the Crystal,” Journal of Molecular Structure, Vol. 553, No. 1-3, 2000, pp. 157-166. doi:10.1016/S0022-2860(00)00578-0
NOTES
*Corresponding author.

