Open Journal of Physical Chemistry
Vol. 2 No. 1 (2012) , Article ID: 17538 , 6 pages DOI:10.4236/ojpc.2012.21006
Buffer Standards for the Biochemical pH of the Zwitterionic Buffer N-Tris-(Hydroxymethyl) Methyl-2-aminoethanesulfonic Acid (TES) from 5˚C to 55˚C
Hoffman Department of Chemistry, Drury University, Springfield, USA
Email: *rroy@drury.edu
Received October 6, 2011; revised November 8, 2011; accepted December 22, 2011
Keywords: Ionic Strength; Liquid Junction Potentials; Second Dissociation Constant; Buffer Solutions; Activity Coefficients
ABSTRACT
The authors have undertaken the determination of pH values for one buffer solution of TES without NaCl and nine buffer solutions with NaCl yielding an ionic strength I = 0.16 mol·kg–1 similar to that of blood. These buffer solutions have been evaluated in the temperature range of 5˚C to 55˚C using an extended version of the Debye-Hückel equation. The pH values are reported using 1) the Debye-Hückel extension of the Bates-Guggenheim convention in the temperature range 5˚C to 55˚C and 2) with and without liquid junction correction at 25˚C and 37˚C. These TES buffer solutions are recommended as secondary standard references for pH measurements in the range of pH 7.2 to 7.5 for physiological application with an ionic strength of I = 0.16 mol·kg–1.
1. Introduction
Good et al. [1,2] have proposed a select group of zwitterionic buffers for physiological use. The authors have previously reported the pH values of N-[tris(hydroxymethyl) methyl-3-amino]propansulfonic acid (TAPS) [3] from 5 to 55˚C, including 37˚C. Vega and Bates [4] have reported the second dissociation constant, pK2, and related thermodynamic data of TES from 5˚C to 55˚C. Roy and associates [5] also determined pK2 values of TES with thermodynamic quantities from 5˚C to 55˚C. The purpose of the current investigation is to provide pH values for the amino acid TES, the structure of which is given in Figure 1.
The universally used NIST certified physiological phosphate primary standard buffer solution has pH values of 7.415 and 7.395 at 25˚C and 37˚C, respectively [6]. This phosphate buffer contains 0.008695 mol·kg−1 KH2PO4 and 0.03043 mol·kg−1 Na2HPO4. Because of problems associated with the current phosphate buffer [7-9], we have been prompted to investigate some zwitterionic buffers including TES for use in physiological pH range 6.5 - 7.5.
The following compositions were used for the determination of paH: 1) (0.08 mol·kg−1) TES + (0.08 mol·kg–1) NaTES, I = 0.08 mol·kg–1;
2) (0.02 mol·kg–1) TES + (0.02 mol·kg–1) NaTES + (0.14 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 3) (0.04 mol·kg–1) TES + (0.04 mol·kg–1) NaTES + (0.12 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 4) (0.06 mol·kg–1) TES + (0.06 mol·kg–1) NaTES + (0.10 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 5) (0.08 mol·kg–1) TES + (0.08 mol·kg–1) NaTES + (0.08 mol·kg–1) NaCl, I = 0.16 mol·kg–1;
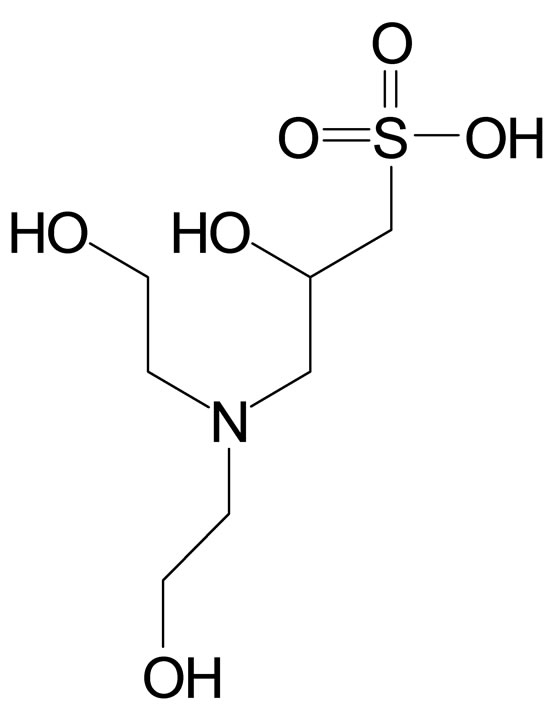
Figure 1. N-tris-(hydroxymethyl)methyl-2-aminoethanesulfonic acid (TES).
6) (0.05 mol·kg–1) TES + (0.05 mol·kg–1) NaTES + (0.11 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 7) (0.02 mol·kg–1) TES + (0.04 mol·kg–1) NaTES + (0.12 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 8) (0.03 mol·kg–1) TES + (0.06 mol·kg–1) NaTES + (0.10 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 9) (0.04 mol·kg–1) TES + (0.08 mol·kg–1) NaTES + (0.08 mol·kg–1) NaCl, I = 0.16 mol·kg–1; 10) (0.05 mol·kg–1) TES + (0.10 mol·kg–1) NaTES + (0.06 mol·kg–1) NaCl, I = 0.16 mol·kg–1.
2. Experimental
The TES was obtained from Research Organics in Cleveland, OH. The experimental method for further crystallization and the assay have been previously reported in detail [5]. Buffer solutions 1) to 10) were prepared by weighing recrystallized TES buffer, ACS reagent grade NaCl, a standard NaOH solution, and calculated amounts of double distilled CO2-free water. Vacuum corrections were made for all masses.
The cell design, preparation of the chloroplatinic acid, hydrogen gas purification, silver-silver chloride, solution preparation, and other experimental details have been described previously [10-13].
3. Methods and Results
Cell (A) contains one solution without the Cl− and nine solutions containing NaCl to yield an ionic strength of I = 0.16 mol·kg–1. The emf values have been corrected to a hydrogen pressure of 1 atm. The values for the paH calculations are given in Table 1. The error in the emf, on an average of two readings, lies within 0.02 mV.
For accurate calculations of the pH values of the buffer solutions, the following Cell (A) was used:
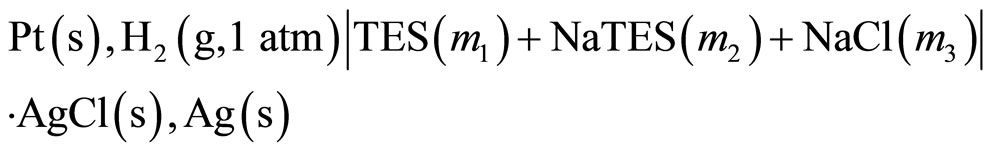 (A)
(A)
where m1, m2, and m3 denote the molalities of the respective species at 1 atm. The Harned-type cell was employed.
Cell (B) involves liquid junction as shown with a double vertical line:
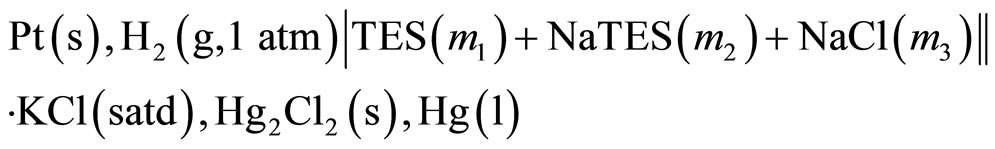 (B)
(B)
where the abbreviations “s”, “l”, and “g” indicate the solid, liquid, and gaseous states, respectively.
For Cell (C), the phosphate salts were NIST standard reference materials. Its solutions are recommended for pH measurements in physiological media. The schematic diagram of the Cell (C) is shown below:
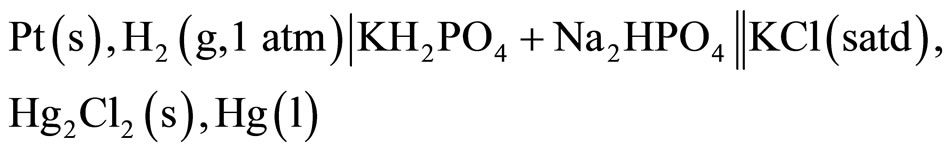 (C)
(C)
The 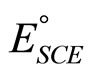 values of the saturated calomel electrode were taken as –0.2415 and –0.2335 at 25˚C and 37˚C, respectively [12,14]. The δEj values of the buffer solution for Cell (B) were calculated using the following equation:
values of the saturated calomel electrode were taken as –0.2415 and –0.2335 at 25˚C and 37˚C, respectively [12,14]. The δEj values of the buffer solution for Cell (B) were calculated using the following equation:
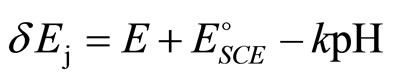 (1)
(1)
where k = 0.059156 and pH = 7.415 at 25˚C; k = 0.061538 and pH = 7.395 at 37˚C. These values are for phosphate primary standard and buffer solutions. The operational definition of pH is denoted as pH(x) which can be calculated by use of the equation:
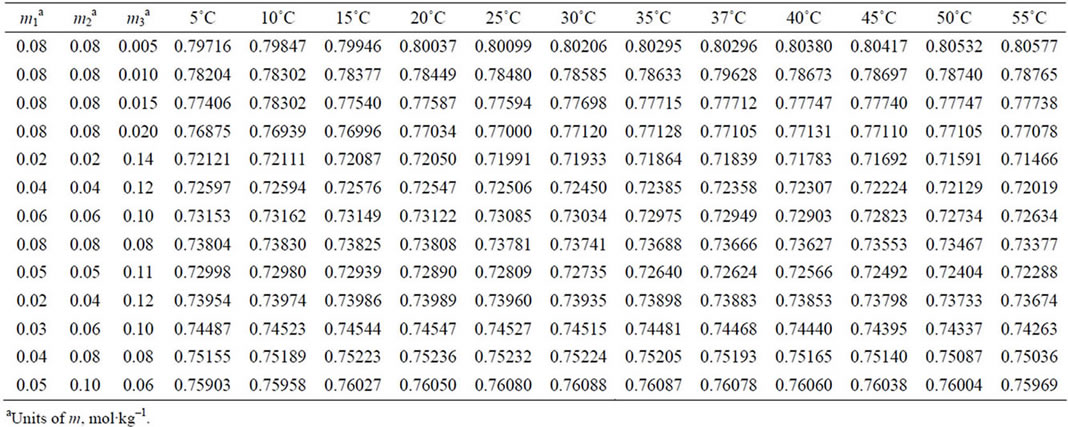
Table 1. Electromotive force of Cell A: .
.
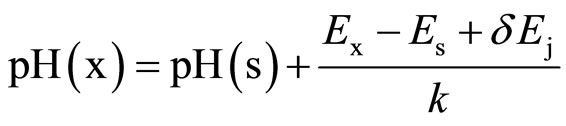 (2)
(2)
where “x” refers to the unknown buffer solution (TES + NaTES in this case), “s” is the NIST standard phosphate buffer solution of known pH, and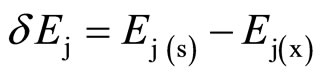 .
.
To calculate the pH values for the buffer solutions, the determination of the acidity function, p(aHgCl), in the temperature range 5˚C to 55˚C is required. These calculations were made using the emf (E) values listed in Table 1. The following equation was used:
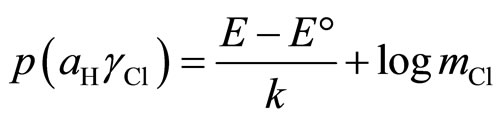 (3)
(3)
where “k” is the Nernst slope.
The plot of 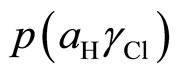 as a function of
as a function of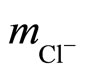 , a linear plot was obtained. The y-intercept gives a
, a linear plot was obtained. The y-intercept gives a 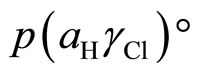 value at
value at . The
. The 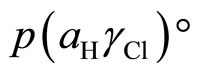 values for the chloride-free buffer solution are listed in Table 2. The
values for the chloride-free buffer solution are listed in Table 2. The  values for the buffer solutions of high ionic strength containing Cl– are entered in Tables 2 and 3 from 5˚C to 55˚C.
values for the buffer solutions of high ionic strength containing Cl– are entered in Tables 2 and 3 from 5˚C to 55˚C.
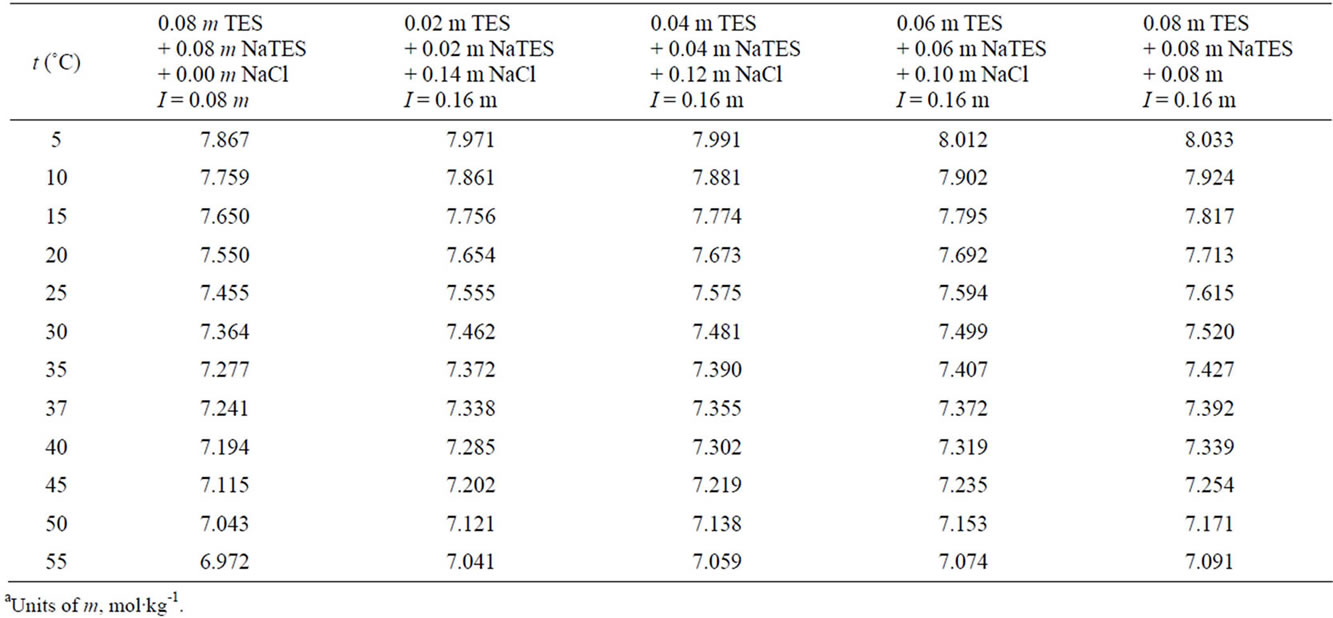
Table 2. 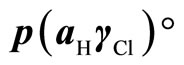 of
of 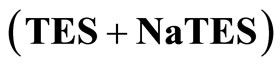 buffer solutions from 5˚C to 55˚C, computed using Equation 5a
buffer solutions from 5˚C to 55˚C, computed using Equation 5a  of
of 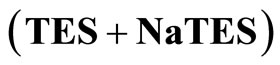 buffer solutions from 5˚C to 55˚C, computed using Equation (4)a.
buffer solutions from 5˚C to 55˚C, computed using Equation (4)a.
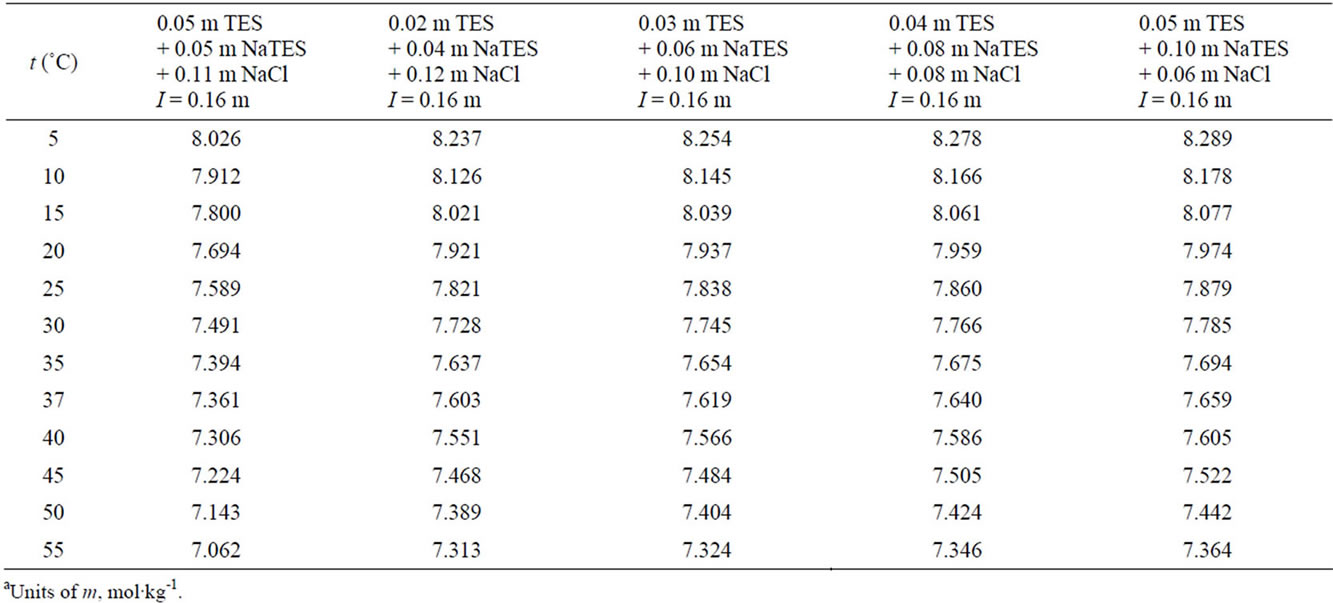
Table 3. 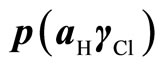 of
of 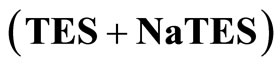 buffer solutions from 5˚C to 55˚C, computed using Equation (4)a.
buffer solutions from 5˚C to 55˚C, computed using Equation (4)a.
The pH(s) values for solutions without liquid junction in the absence of NaCl were determined using the next Equation:
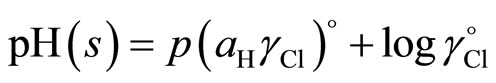 (4)
(4)
where the single-ion activity coefficient, 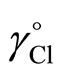 , cannot be experimentally measured. A previous publication gives the method used for obtaining
, cannot be experimentally measured. A previous publication gives the method used for obtaining  [10,15,16]. The pH values from the liquid junction cell are indicated by pH whereas the “conventional” pH calculated from Equayon. 5 is designated as pH(s). The Bates-Guggenheim convention [10,15] is commonly known as “pH convention” and is expressed by the Equation:
[10,15,16]. The pH values from the liquid junction cell are indicated by pH whereas the “conventional” pH calculated from Equayon. 5 is designated as pH(s). The Bates-Guggenheim convention [10,15] is commonly known as “pH convention” and is expressed by the Equation:
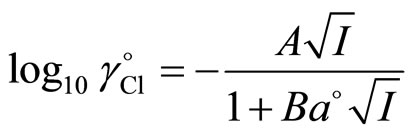 (5)
(5)
where Equation (5) is valid only up to 0.1 mol·kg−1. Since blood and other physiological solutions have I = 0.16 mol·kg–1, there is a need for a better choice to calculate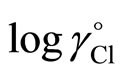 . Thus, a linear-dependent “CI” term is added in the Bates-Guggenheim convention as shown in Equation (6):
. Thus, a linear-dependent “CI” term is added in the Bates-Guggenheim convention as shown in Equation (6):
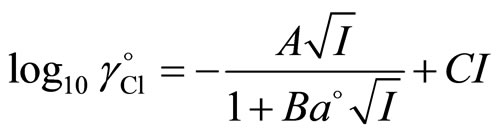 (6)
(6)
where “I” is the ionic strength of the buffer solution, the constants “A”, “B”, and a˚ have the usual physical significances. The following empirical equation is used for the calculation of the adjustable parameter “C” [8,10].
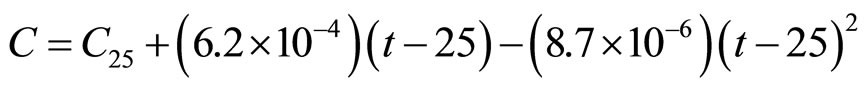 (7)
(7)
where C25= 0.032 kg·mol–1 at 25˚C and t is the temperature in degrees Celsius.
The paH values listed in Tables 4 and 5 for the TES buffer solution with and without the presence of NaCl
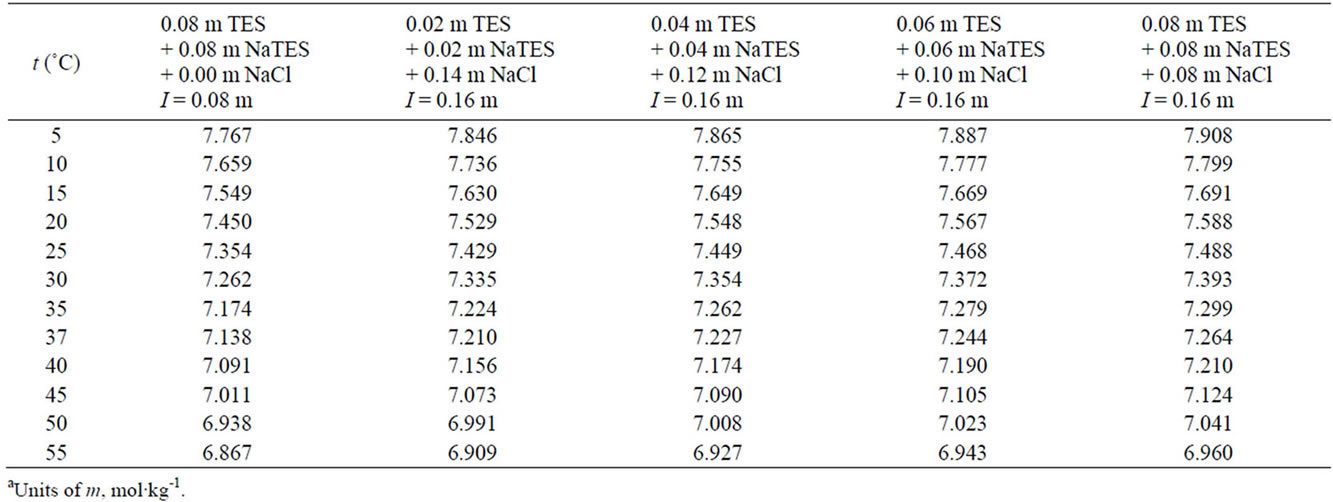
Table 4.  of
of  buffer solutions from 5˚C to 55˚C, computed using Equations (4)-(6)a.
buffer solutions from 5˚C to 55˚C, computed using Equations (4)-(6)a.
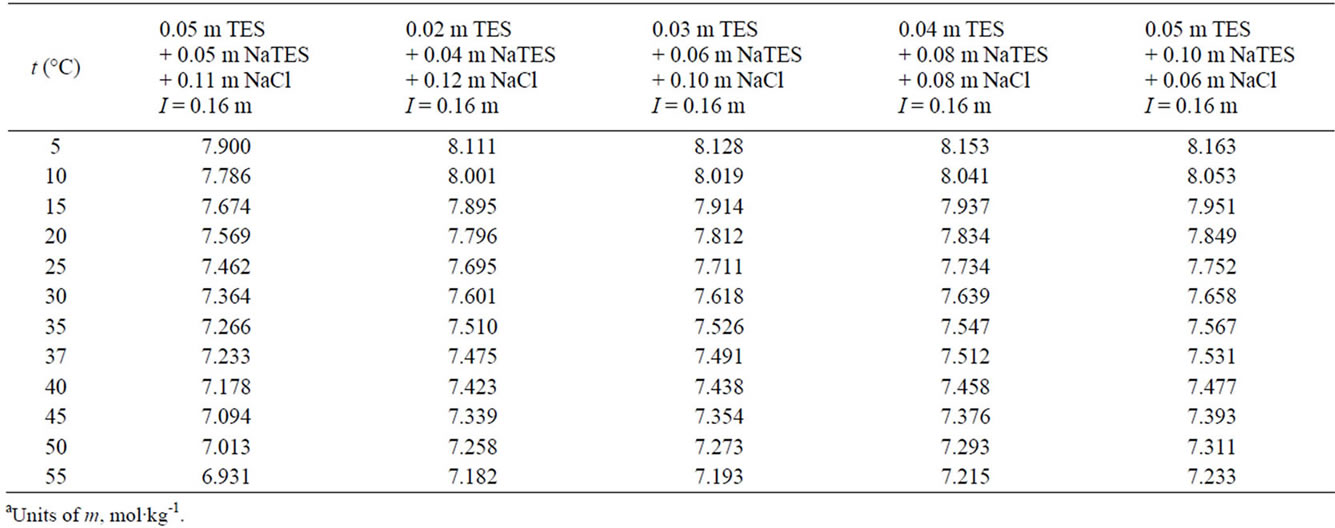
Table 5. 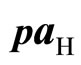 of
of 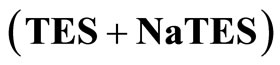 buffer solutions from 5˚C to 55˚C, computed using Equations (4)-(6)a.
buffer solutions from 5˚C to 55˚C, computed using Equations (4)-(6)a.
were calculated using the following equation:
1)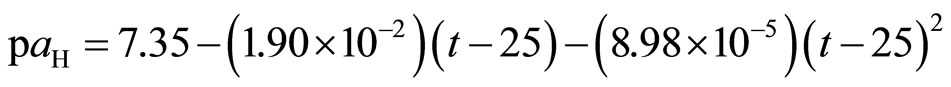 (8)
(8)
in the temperature range of 5˚C to 55˚C. The standard deviation of regression for the paH of the chloride-free buffer solution was obtained using Equations (3), (4), (6), and (7). The standard deviation was 0.0012.
For the buffer solutions containing NaCl, with an isotonic saline media ionic strength of I = 0.16 mol·kg–1, the paH values were also calculated using Equations. 3 - 7. The acidity function data, 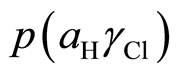 from Tables 2 and 3 were used to generate the paH data entered in Tables 4 and 5. These paH values are expressed by use of the quadratic equations:
from Tables 2 and 3 were used to generate the paH data entered in Tables 4 and 5. These paH values are expressed by use of the quadratic equations:
2)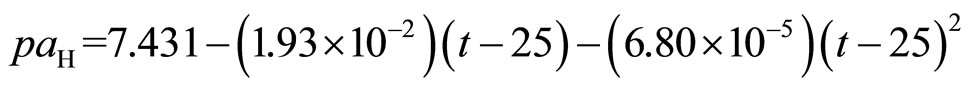 (9)
(9)
3)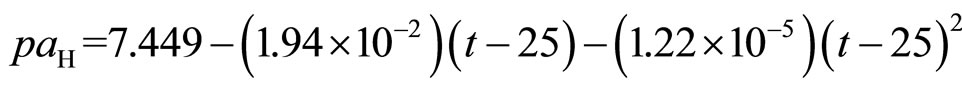 (10)
(10)
4)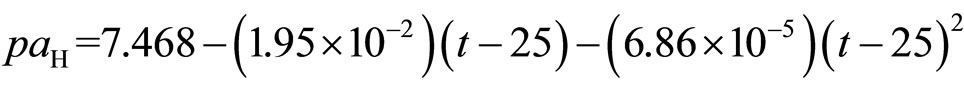 (11)
(11)
5)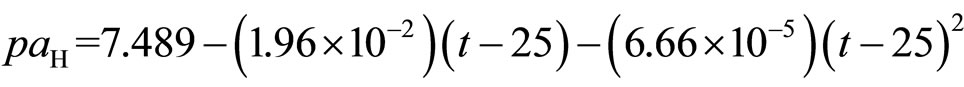 (12)
(12)
6)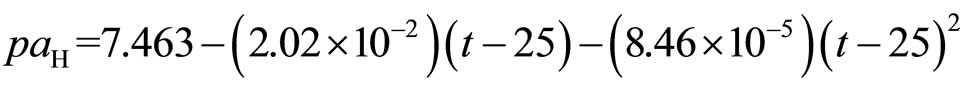 (13)
(13)
7)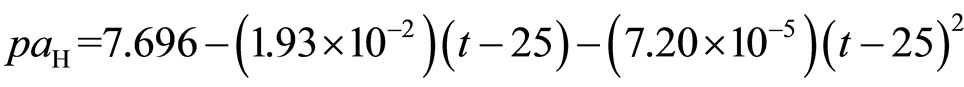 (14)
(14)
8) (15)
(15)
9) (16)
(16)
10)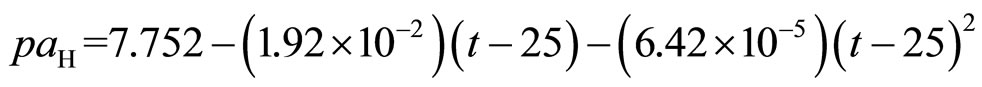 (17)
(17)
The observed standard deviations of regression from Equations. 9 - 17 are 0.0014, 0.0009, 0.0006, 0.0006, 0.0009, 0.0008, 0.0010, 0.0009, and 0.0009, respectively.
The emf values of Cells (B) and (C), pH values with and without liquid junction, an the values of δEj at 25 and 37˚C are given in Table 6. These are various sources of error: 1) extrapolation of the 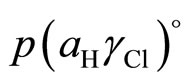 plot for Cl− free solutions; 2) the calculation of the single ion activity coefficient
plot for Cl− free solutions; 2) the calculation of the single ion activity coefficient  using Equation (6); 3) the error in the experimental emf measurement; and 4) in the estimation of the liquid junction potential. For the four buffer solutions in Table 6 the pH values obtained from the extended Debye-Hückel equations and liquid junction correction are in very good agreement (±0.001 pH unit). Thus these TES buffer solutions are recommended as useful secondary pH standard for blood serum and physiological application in the pH range 7.2 - 7.5. The authors have undertaken the calculation of the single ion
using Equation (6); 3) the error in the experimental emf measurement; and 4) in the estimation of the liquid junction potential. For the four buffer solutions in Table 6 the pH values obtained from the extended Debye-Hückel equations and liquid junction correction are in very good agreement (±0.001 pH unit). Thus these TES buffer solutions are recommended as useful secondary pH standard for blood serum and physiological application in the pH range 7.2 - 7.5. The authors have undertaken the calculation of the single ion
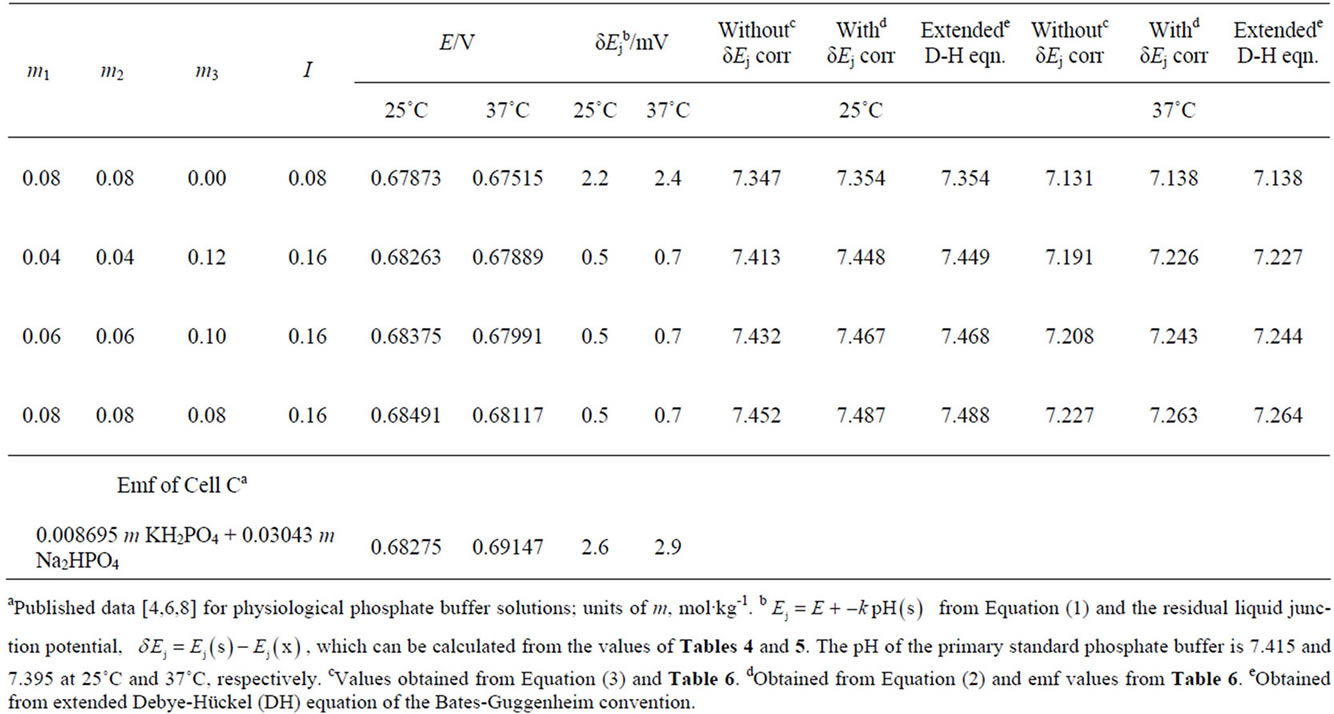
Table 6. Emf of Cell B and pH values with δEj correction at 25˚C and 37˚C for TES buffer.
activity coefficient need for accurate pH calculation of several buffer solutions using Pitzer formalism [17,18].
4. Acknowledgements
The authors are grateful for the funding from the National Institutes of Health (AREA), under the grant 2- R15 GM 066866-03 and the diversity supplemental grant 3-R15 GM 066866-03 S1. The authors would also like to thank Ethan Graham and Chad Lunn for their dedication and hard work. The content of this paper is the sole responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the National Institutes of General Medical Sciences.
REFERENCES
- N. E. Good, G. D. Winget, W. Winter, T. N. Connolly, S. Izawa and R. M. M. Singh, “Hydrogen Ion Buffers for Biological Research,” Biochemistry, Vol. 5, No. 2, 1966, pp. 467-477. doi:10.1021/bi00866a011
- W. J. Ferguson, K. L. Braunschweiger, W. R. Braunschweiger, J. R. Smith, J. J. McCormick, C. C. Wasmann, N. P. Jarvis, D. H. Bell and N. E. Good, “Hydrogen Ion Buffers for Biological Research,” Analytical Biochemistry, Vol. 104, No. 2, 1980, pp. 300-310. doi:10.1016/0003-2697(80)90079-2
- L. N. Roy, R. N. Roy, C. E. Denton, S. R. Le Noue, C. A. Himes, S. J. Richards, A. N. Simon and V. S. Somal, “Buffer Standards for the Physiological pH of the Zwitterionic Compound, TAPS, from 5˚C to 55˚C,” Journal of Solution Chemistry, Vol. 35, 2006, pp. 551-556. doi:10.1007/s10953-005-9010-0
- C. A. Vega and R. G. Bates, “Buffers for the Physiological pH Range: Thermodynamic Constants of Four Substituted Aminoethanesulfonic Acids from 5˚C to 50˚C,” Analytical Chemistry, Vol. 48, No. 9, 1976, pp. 1293-1296.
- R. N. Roy, C. P. Moore, J. A. Carlsten, W. S. Good, P. Harris, J. M. Rook, L. N. Roy and K. M. Kuhler, “Second Dissociation Constants of Two Substituted Aminoethanesulfonic Acids (MES) and (TES) in Water from 5˚C to 55˚C,” Journal of Solution Chemistry, Vol. 26, No. 12, 1997, pp. 1209-1216. doi:10.1023/A:1022937324983
- V. E. Bower, M. Paabo and R. G. Bates, “A Standard for the Measurement of the pH of Blood and Other Physiological Media,” Journal of Research of the National Bureau of Standards, Vol. 65A, No. 3, 1961, pp. 267-270.
- R. A. Durst and B. R. Staples, “Tris/Tris HCl: Standard Buffer for Use in the Physiological pH Range,” Clinical Chemistry, Vol. 18, No. 3, 1972, pp. 206-208.
- D. Feng, W. F. Koch and Y. C. Wu, “Second Dissociation Constant and pH of N-(2-Hydroxyethyl)-piperazine-N’-2-ethanesulfonic Acid from 0˚C to 50˚C,” Analytical Chemistry, Vol. 61, 1989, pp. 1400-1405. doi:10.1021/ac00188a019
- Y. C. Wu, P. A. Berezansky, D. Feng and W. F. Koch, “Second Dissociation Constant of 3-(N-Morpholino)-2-hydroxypropanesulfonic Acid and pH of Its Buffer Solutions,” Analytical Chemistry, Vol. 65, 1993, pp. 1084-1987. doi:10.1021/ac00056a023
- R. N. Roy, D. R. Mrad, P. A. Lord, J. A. Carlsten, W. S. Good, P. Allsup, L. N. Roy, K. M. Kuhler, W. F. Koch and Y. C. Wu, “Thermodynamics of the Second Dissociation Constant and Standards for pH of 3-(N-Morpholino)propanesulfonic Acid (MOPS) from 5˚C to 55˚C,” Journal of Solution Chemistry, Vol. 27, No. 1, 1998, pp. 73-87. doi:10.1023/A:1022692629289
- R. G. Bates, C. A. Vega and D. R. White Jr., “Standards for pH Measurements in Isotonic Saline Media of Ionic Strength I = 0.16,” Analytical Chemistry, Vol. 50, No. 9, 1978, pp. 1295-1300. doi:10.1021/ac50031a026
- R. G. Bates, “Determination of pH,” 2nd Edition, Wiley, New York, 1973.
- R. N. Roy, L. N. Roy, C. E. Denton, S. R. LeNoue, S. Ashkenazi, M. S. Fuge, C. D. Dunseth, J. L. Durden, C. N. Roy, A. Bwashi, J. T. Wollen and S. J. DeArmon, “Buffer Standards for the Physiological pH of 3-[(1,1-Dimethyl-2-hydroxymethyl)-amino]-2-hydroxypropanesulfonic Acid from (278.15 to 328.15) K,” Journal of Chemical & Engineering Data, Vol. 54, No. 2, 2009, pp. 428-435.
- W. M. Latimer, “Oxidation Potentials,” 2nd Edition, Prentice-Hall, New York, 1952.
- R. G. Bates and E. A. Guggenheim, “Report on the Standardization of pH and Related Terminology,” Pure and Applied Chemistry, Vol. 1, No. 1, 1960, pp. 163-168. doi:10.1351/pac196001010163
- R. N. Roy, L. N. Roy, S. Ashkenazi, J. T. Wollen, C. D. Dunseth, M. S. Fuge, C. N. Roy, H. M. Hughes, B. T. Morris and K. L. Cline, “Buffer Standards for pH Measurement of N-(2-Hydroxyethyl)piperazine-N’-2-ethanesulfonic Acid (HEPES) for I = 0.16 mol·kg−1 from 5˚C to 55˚C,” Journal of Solution Chemistry, Vol. 38, 2009, pp. 449-458. doi:10.1007/s10953-009-9378-3
- K. S. Pitzer and G. J. Mayorga, “Thermodynamics of Electrolytes. II. Activity and Osmotic Coefficients for Strong Electrolytes with One or Both Ions Univalent,” Journal of Physical Chemistry, Vol. 77, No. 19, 1973, pp. 2300-2307. doi:10.1021/j100638a009
- R. P. Buck, S. Rondinini, A. K. Covington, F. G. K. Baucke, C. M. A. Brett, M. F. Camões, M. J. T. Milton, T. Mussini, R. Naumann, K. W. Pratt, P. Spitzer and G. S. Wilson, “Measurement of pH: Definition, Standards, and Procedures,” Pure and Applied Chemistry, Vol. 74, No. 11, 2002, pp. 2169-2200. doi:10.1351/pac200274112169
NOTES
*Corresponding author.

